Teorema de la línea Droz-Farny

En geometría euclidiana , el teorema de la línea Droz-Farny es una propiedad de dos líneas perpendiculares que pasan por el ortocentro de un triángulo arbitrario.

Sea un triángulo con vértices , , y , y sea su ortocentro (el punto común de sus tres líneas de altura . Sean y sean dos líneas perpendiculares entre sí que pasen por . Sean , , y los puntos donde interseca las líneas laterales , , y , respectivamente. De manera similar, sean , , y los puntos donde interseca esas líneas laterales. El teorema de la línea Droz-Farny dice que los puntos medios de los tres segmentos , , y son colineales . ^{[1] [2] [3]}${\estilo de visualización T}$${\estilo de visualización A}$${\estilo de visualización B}$${\estilo de visualización C}$${\estilo de visualización H}$$Estilo de visualización L_{1}$$Estilo de visualización L_{2}$${\estilo de visualización H}$$Estilo de visualización A_{1}$$Estilo de visualización B_{1}$$Estilo de visualización C_{1}$$Estilo de visualización L_{1}$${\displaystyle BC}$${\displaystyle CA}$${\estilo de visualización AB}$$Estilo de visualización A_{2}$$Estilo de visualización B_{2}$$Estilo de visualización C_{2}$$Estilo de visualización L_{2}$$Estilo de visualización A_{1}A_{2}}$$Estilo de visualización B_{1}B_{2}}$$Estilo de visualización C_{1}C_{2}}$

El teorema fue enunciado por Arnold Droz-Farny en 1899, ^[1] pero no está claro si tenía una prueba. ^[4]

En 1930, René Goormaghtigh demostró una generalización del teorema de la línea Droz-Farny . ^[5]

Como se indica arriba, sea un triángulo con vértices , , y . Sea cualquier punto distinto de , , y , y cualquier línea que pase por . Sean , , y puntos en las líneas laterales , , y , respectivamente, tales que las líneas , , y son las imágenes de las líneas , , y , respectivamente, por reflexión sobre la línea . El teorema de Goormaghtigh dice entonces que los puntos , , y son colineales.${\estilo de visualización T}$${\estilo de visualización A}$${\estilo de visualización B}$${\estilo de visualización C}$${\estilo de visualización P}$${\estilo de visualización A}$${\estilo de visualización B}$${\estilo de visualización C}$${\estilo de visualización L}$${\estilo de visualización P}$$Estilo de visualización A_{1}$$Estilo de visualización B_{1}$$Estilo de visualización C_{1}$${\displaystyle BC}$${\displaystyle CA}$${\estilo de visualización AB}$$Estilo de visualización PA_{1}$$Estilo de visualización PB_{1}$$Estilo de visualización PC_{1}$${\estilo de visualización PA}$${\estilo de visualización PB}$${\estilo de visualización PC}$${\estilo de visualización L}$$Estilo de visualización A_{1}$$Estilo de visualización B_{1}$$Estilo de visualización C_{1}$

El teorema de la línea Droz-Farny es un caso especial de este resultado, cuando es el ortocentro del triángulo .${\estilo de visualización P}$${\estilo de visualización T}$

El teorema fue generalizado posteriormente por Dao Thanh Oai, de la siguiente manera:

Primera generalización: Sea ABC un triángulo, P un punto del plano, sean tres segmentos paralelos AA', BB', CC' tales que sus puntos medios y P sean colineales. Entonces PA', PB', PC' se cortan con BC, CA, AB respectivamente en tres puntos colineales. ^[6]

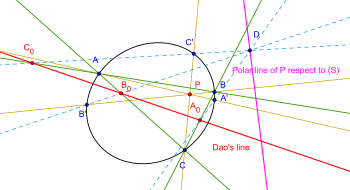
Segunda generalización: Sea una cónica S y un punto P en el plano . Construya tres rectas d _a , d _b , d _c a través de P tales que corten la cónica en A, A'; B, B' ; C, C' respectivamente. Sea D un punto en la polar del punto P con respecto a (S) o D se encuentra en la cónica (S). Sea DA' ∩ BC =A ₀ ; DB' ∩ AC = B ₀ ; DC' ∩ AB= C ₀ . Entonces A ₀ , B ₀ , C ₀ son colineales. ^{[7] [8] [9]}