La kappa de Cohen
El coeficiente kappa de Cohen ( κ , kappa en minúscula del griego ) es una estadística que se utiliza para medir la fiabilidad entre evaluadores (y también la fiabilidad intraevaluador ) para ítems cualitativos (categóricos). [1] En general, se piensa que es una medida más robusta que el simple cálculo del porcentaje de acuerdo, ya que κ tiene en cuenta la posibilidad de que el acuerdo se produzca por casualidad. Existe controversia en torno al kappa de Cohen debido a la dificultad de interpretar los índices de acuerdo. Algunos investigadores han sugerido que es conceptualmente más simple evaluar el desacuerdo entre ítems. [2]
Historia
La primera mención de una estadística similar a kappa se atribuye a Galton en 1892. [3] [4]
El artículo seminal que introdujo kappa como una nueva técnica fue publicado por Jacob Cohen en la revista Educational and Psychological Measurement en 1960. [5]
Definición
La kappa de Cohen mide el acuerdo entre dos evaluadores que clasifican cada uno N elementos en C categorías mutuamente excluyentes. La definición de es
donde p o es el acuerdo relativo observado entre los evaluadores, y p e es la probabilidad hipotética de acuerdo casual, utilizando los datos observados para calcular las probabilidades de que cada observador seleccione aleatoriamente cada categoría. Si los evaluadores están completamente de acuerdo, entonces . Si no hay acuerdo entre los evaluadores más allá de lo que se esperaría por casualidad (como se da por p e ), . Es posible que la estadística sea negativa, [6] lo que puede ocurrir por casualidad si no hay relación entre las calificaciones de los dos evaluadores, o puede reflejar una tendencia real de los evaluadores a dar calificaciones diferentes.
Para k categorías, N observaciones a categorizar y el número de veces que el evaluador i predijo la categoría k :
Esto se deriva de la siguiente construcción:
Donde es la probabilidad estimada de que tanto el evaluador 1 como el evaluador 2 clasifiquen el mismo elemento como k, mientras que es la probabilidad estimada de que el evaluador 1 clasifique un elemento como k (y de manera similar para el evaluador 2). La relación se basa en el uso del supuesto de que la calificación de los dos evaluadores es independiente . El término se estima utilizando el número de elementos clasificados como k por el evaluador 1 ( ) dividido por el total de elementos a clasificar ( ): (y de manera similar para el evaluador 2).
Matriz de confusión de clasificación binaria
En la matriz de confusión 2 × 2 tradicional empleada en el aprendizaje automático y las estadísticas para evaluar clasificaciones binarias , la fórmula Kappa de Cohen se puede escribir como: [7]
donde TP son los verdaderos positivos, FP son los falsos positivos, TN son los verdaderos negativos y FN son los falsos negativos. En este caso, el Kappa de Cohen es equivalente a la puntuación de habilidad de Heidke conocida en meteorología . [8] La medida fue introducida por primera vez por Myrick Haskell Doolittle en 1888. [9]
Ejemplos
Ejemplo sencillo
Supongamos que se analizan los datos relacionados con un grupo de 50 personas que solicitan una subvención. Cada propuesta de subvención es leída por dos lectores y cada uno de ellos responde "Sí" o "No" a la propuesta. Supongamos que los datos de recuento de desacuerdos son los siguientes, donde A y B son los lectores, los datos de la diagonal principal de la matriz (a y d) cuentan el número de acuerdos y los datos fuera de la diagonal (b y c) cuentan el número de desacuerdos:
B A | Sí | No |
|---|---|---|
| Sí | a | b |
| No | do | d |
p.ej
B A | Sí | No |
|---|---|---|
| Sí | 20 | 5 |
| No | 10 | 15 |
El acuerdo proporcional observado es:
Para calcular p e (la probabilidad de acuerdo aleatorio) observamos que:
- El lector A respondió "Sí" a 25 solicitantes y "No" a 25 solicitantes. Por lo tanto, el lector A respondió "Sí" el 50% de las veces.
- El lector B respondió "Sí" a 30 solicitantes y "No" a 20. Por lo tanto, el lector B respondió "Sí" el 60% de las veces.
Entonces la probabilidad esperada de que ambos digan que sí al azar es:
Similarmente:
La probabilidad general de acuerdo aleatorio es la probabilidad de que estén de acuerdo en Sí o No, es decir:
Así que ahora aplicando nuestra fórmula para Kappa de Cohen obtenemos:
Mismos porcentajes pero diferentes números
Un caso que a veces se considera un problema con el Kappa de Cohen ocurre cuando se compara el Kappa calculado para dos pares de evaluadores en los que los dos evaluadores de cada par tienen el mismo porcentaje de acuerdo, pero un par da una cantidad similar de calificaciones en cada clase, mientras que el otro par da una cantidad muy diferente de calificaciones en cada clase. [10] (En los casos siguientes, observe que B tiene 70 síes y 30 noes, en el primer caso, pero esos números están invertidos en el segundo). Por ejemplo, en los dos casos siguientes hay un acuerdo igual entre A y B (60 de 100 en ambos casos) en términos de acuerdo en cada clase, por lo que esperaríamos que los valores relativos del Kappa de Cohen reflejen esto. Sin embargo, al calcular el Kappa de Cohen para cada uno:
B A | Sí | No |
|---|---|---|
| Sí | 45 | 15 |
| No | 25 | 15 |
B A | Sí | No |
|---|---|---|
| Sí | 25 | 35 |
| No | 5 | 35 |
Observamos que en el segundo caso se observa una mayor similitud entre A y B que en el primero. Esto se debe a que, si bien el porcentaje de acuerdo es el mismo, el porcentaje de acuerdo que se daría "por casualidad" es significativamente mayor en el primer caso (0,54 frente a 0,46).
Propiedades
Prueba de hipótesis e intervalo de confianza
El valor p para kappa rara vez se informa, probablemente porque incluso valores relativamente bajos de kappa pueden, no obstante, ser significativamente diferentes de cero pero no de magnitud suficiente para satisfacer a los investigadores. [11] : 66 Aun así, su error estándar ha sido descrito [12] y se calcula mediante varios programas informáticos. [13]
Se pueden construir intervalos de confianza para Kappa, para los valores Kappa esperados si tuviéramos un número infinito de elementos seleccionados, utilizando la siguiente fórmula: [1]
¿Dónde está el percentil normal estándar cuando , y
Esto se calcula ignorando que p e se estima a partir de los datos y tratando p o como una probabilidad estimada de una distribución binomial mientras se utiliza la normalidad asintótica (es decir: asumiendo que el número de elementos es grande y que p o no está cerca de 0 o 1). (y el IC en general) también se puede estimar utilizando métodos bootstrap .
Interpretación de la magnitud

Si la significación estadística no es una guía útil, ¿qué magnitud de kappa refleja un acuerdo adecuado? Serían útiles las pautas, pero otros factores además del acuerdo pueden influir en su magnitud, lo que hace que la interpretación de una magnitud dada sea problemática. Como señalaron Sim y Wright, dos factores importantes son la prevalencia (¿son los códigos equiprobables o varían sus probabilidades?) y el sesgo (¿son las probabilidades marginales para los dos observadores similares o diferentes?). En igualdad de condiciones, los kappas son más altos cuando los códigos son equiprobables. Por otro lado, los kappas son más altos cuando los códigos se distribuyen asimétricamente por los dos observadores. A diferencia de las variaciones de probabilidad, el efecto del sesgo es mayor cuando el kappa es pequeño que cuando es grande. [14] : 261–262
Otro factor es el número de códigos. A medida que aumenta el número de códigos, los kappas se vuelven más altos. Basándose en un estudio de simulación, Bakeman y sus colegas concluyeron que para los observadores falibles, los valores de kappa eran más bajos cuando los códigos eran menos. Y, de acuerdo con la afirmación de Sim & Wrights sobre la prevalencia, los kappas eran más altos cuando los códigos eran aproximadamente equiprobables. Así, Bakeman et al. concluyeron que "ningún valor de kappa puede considerarse universalmente aceptable". [15] : 357 También proporcionan un programa informático que permite a los usuarios calcular valores para kappa especificando el número de códigos, su probabilidad y la precisión del observador. Por ejemplo, dados los códigos equiprobables y los observadores que tienen una precisión del 85%, los valores de kappa son 0,49, 0,60, 0,66 y 0,69 cuando el número de códigos es 2, 3, 5 y 10, respectivamente.
No obstante, en la literatura han aparecido directrices sobre la magnitud. Quizás la primera fue la de Landis y Koch [16] , que caracterizaron los valores < 0 como indicativos de falta de acuerdo, los de 0 a 0,20 como leves, los de 0,21 a 0,40 como regulares, los de 0,41 a 0,60 como moderados, los de 0,61 a 0,80 como sustanciales y los de 0,81 a 1 como casi perfectos. Sin embargo, este conjunto de directrices no es de ninguna manera universalmente aceptado; Landis y Koch no aportaron ninguna evidencia para respaldarlo, sino que lo basaron en su opinión personal. Se ha observado que estas directrices pueden ser más perjudiciales que útiles. [17] Las directrices igualmente arbitrarias de Fleiss [18] : 218 caracterizan los kappas superiores a 0,75 como excelentes, los de 0,40 a 0,75 como regulares a buenos y los inferiores a 0,40 como malos.
Máximo kappa
Kappa asume su valor máximo teórico de 1 solo cuando ambos observadores distribuyen los códigos de la misma manera, es decir, cuando las sumas de filas y columnas correspondientes son idénticas. Cualquier valor menor es una concordancia menos que perfecta. Aun así, el valor máximo que kappa podría alcanzar dadas distribuciones desiguales ayuda a interpretar el valor de kappa realmente obtenido. La ecuación para κ máximo es: [19]
donde , como de costumbre ,
k = número de códigos, son las probabilidades de fila y son las probabilidades de columna.
Limitaciones
Kappa es un índice que considera el acuerdo observado con respecto a un acuerdo de referencia. Sin embargo, los investigadores deben considerar cuidadosamente si el acuerdo de referencia de Kappa es relevante para la pregunta de investigación en particular. La referencia de Kappa se describe con frecuencia como el acuerdo debido al azar, lo cual es solo parcialmente correcto. El acuerdo de referencia de Kappa es el acuerdo que se esperaría debido a la asignación aleatoria, dadas las cantidades especificadas por los totales marginales de la tabla de contingencia cuadrada. Por lo tanto, κ = 0 cuando la asignación observada es aparentemente aleatoria, independientemente del desacuerdo de cantidad según lo restringido por los totales marginales. Sin embargo, para muchas aplicaciones, los investigadores deberían estar más interesados en el desacuerdo de cantidad en los totales marginales que en el desacuerdo de asignación como se describe en la información adicional en la diagonal de la tabla de contingencia cuadrada. Por lo tanto, para muchas aplicaciones, la referencia de Kappa es más una distracción que una aclaración. Considere el siguiente ejemplo:
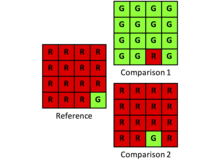
| Referencia | |||
|---|---|---|---|
| GRAMO | R | ||
| Comparación | GRAMO | 1 | 14 |
| R | 0 | 1 | |
La proporción de desacuerdo es 14/16 o 0,875. El desacuerdo se debe a la cantidad porque la asignación es óptima. κ es 0,01.
| Referencia | |||
|---|---|---|---|
| GRAMO | R | ||
| Comparación | GRAMO | 0 | 1 |
| R | 1 | 14 | |
La proporción de desacuerdo es 2/16 o 0,125. El desacuerdo se debe a la asignación porque las cantidades son idénticas. El coeficiente kappa es -0,07.
En este caso, informar sobre el desacuerdo en la cantidad y la asignación es informativo, mientras que Kappa oculta información. Además, Kappa presenta algunos desafíos en el cálculo y la interpretación porque Kappa es un cociente. Es posible que el cociente de Kappa devuelva un valor indefinido debido a que el denominador es cero. Además, un cociente no revela ni su numerador ni su denominador. Es más informativo para los investigadores informar sobre el desacuerdo en dos componentes, cantidad y asignación. Estos dos componentes describen la relación entre las categorías con más claridad que una sola estadística de resumen. Cuando la precisión predictiva es el objetivo, los investigadores pueden comenzar a pensar más fácilmente en formas de mejorar una predicción utilizando dos componentes de cantidad y asignación, en lugar de un cociente de Kappa. [2]
Algunos investigadores han expresado su preocupación por la tendencia de κ a tomar las frecuencias de las categorías observadas como dadas, lo que puede hacer que no sea confiable para medir el acuerdo en situaciones como el diagnóstico de enfermedades raras. En estas situaciones, κ tiende a subestimar el acuerdo sobre la categoría rara. [20] Por esta razón, κ se considera una medida de acuerdo demasiado conservadora. [21] Otros [22] [ cita requerida ] cuestionan la afirmación de que kappa "toma en cuenta" el acuerdo aleatorio. Para hacer esto de manera efectiva, se requeriría un modelo explícito de cómo el azar afecta las decisiones del evaluador. El llamado ajuste aleatorio de las estadísticas kappa supone que, cuando no están completamente seguros, los evaluadores simplemente adivinan, un escenario muy poco realista. Además, algunos trabajos [23] han demostrado cómo las estadísticas kappa pueden llevar a una conclusión errónea para datos desequilibrados.
Estadísticas relacionadas
Pi de Scott
Scott (1955) propuso una estadística similar, denominada pi . El kappa de Cohen y el pi de Scott difieren en cuanto a cómo se calcula p e .
Kappa de Fleiss
Tenga en cuenta que el kappa de Cohen mide el acuerdo entre dos evaluadores únicamente. Para una medida similar de acuerdo ( kappa de Fleiss ) utilizada cuando hay más de dos evaluadores, consulte Fleiss (1971). Sin embargo, el kappa de Fleiss es una generalización de la estadística pi de Scott para varios evaluadores , no el kappa de Cohen. El kappa también se utiliza para comparar el rendimiento en el aprendizaje automático , pero se sostiene que la versión direccional conocida como Informedness o estadística J de Youden es más apropiada para el aprendizaje supervisado. [24]
Kappa ponderado
La kappa ponderada permite ponderar los desacuerdos de forma diferente [25] y es especialmente útil cuando se ordenan los códigos. [11] : 66 Hay tres matrices involucradas, la matriz de puntuaciones observadas, la matriz de puntuaciones esperadas basadas en el acuerdo aleatorio y la matriz de ponderación. Las celdas de la matriz de ponderación ubicadas en la diagonal (de arriba a la izquierda a abajo a la derecha) representan el acuerdo y, por lo tanto, contienen ceros. Las celdas fuera de la diagonal contienen ponderaciones que indican la gravedad de ese desacuerdo. A menudo, las celdas que están una fuera de la diagonal tienen una ponderación de 1, las dos de 2, etc.
La ecuación para κ ponderado es:
donde k = número de códigos y , , y son elementos en las matrices de ponderación, observada y esperada, respectivamente. Cuando las celdas diagonales contienen ponderaciones de 0 y todas las celdas fuera de la diagonal tienen ponderaciones de 1, esta fórmula produce el mismo valor de kappa que el cálculo dado anteriormente.
Véase también
Lectura adicional
- Banerjee, M.; Capozzoli, Michelle; McSweeney, Laura; Sinha, Debajyoti (1999). "Más allá de Kappa: una revisión de las medidas de acuerdo entre evaluadores". Revista Canadiense de Estadística . 27 (1): 3–23. doi :10.2307/3315487. JSTOR 3315487. S2CID 37082712.
- Chicco, D.; Warrens, MJ; Jurman, G. (2021). "El coeficiente de correlación de Matthews (MCC) es más informativo que la puntuación Kappa y Brier de Cohen en la evaluación de la clasificación binaria". IEEE Access . 9 : 78368–81. Bibcode :2021IEEEA...978368C. doi : 10.1109/access.2021.3084050 . hdl : 10281/430460 . S2CID 235308708.
- Cohen, Jacob (1960). "Un coeficiente de acuerdo para escalas nominales". Medición educativa y psicológica . 20 (1): 37–46. doi :10.1177/001316446002000104. hdl : 1942/28116 . S2CID 15926286.
- Cohen, J. (1968). "Kappa ponderada: acuerdo de escala nominal con previsión de desacuerdo escalonado o crédito parcial". Psychological Bulletin . 70 (4): 213–220. doi :10.1037/h0026256. PMID 19673146.
- Fleiss, JL; Cohen, J. (1973). "La equivalencia de kappa ponderado y el coeficiente de correlación intraclase como medidas de fiabilidad". Medición educativa y psicológica . 33 (3): 613–9. doi :10.1177/001316447303300309. S2CID 145183399.
- Sim, J.; Wright, CC (2005). "El estadístico Kappa en estudios de fiabilidad: uso, interpretación y requisitos de tamaño de muestra". Fisioterapia . 85 (3): 257–268. doi : 10.1093/ptj/85.3.257 . PMID 15733050.
- Warrens, J. (2011). "El kappa de Cohen es un promedio ponderado". Metodología estadística . 8 (6): 473–484. doi : 10.1016/j.stamet.2011.06.002 . hdl : 1887/18062 .
Enlaces externos
- Kappa, su significado, problemas y varias alternativas (Enlace inactivo a partir del 16/12/2022)
- Estadísticas Kappa: pros y contras
- Implementaciones de software
- Programa de Windows "ComKappa" para kappa, kappa ponderado y kappa máximo (Error "Acceso denegado (Código de error 1020)" a partir del 16/12/2022)
Referencias
- ^ ab McHugh, Mary L. (2012). "Confiabilidad entre evaluadores: la estadística kappa". Biochemia Medica . 22 (3): 276–282. doi :10.11613/bm.2012.031. PMC 3900052 . PMID 23092060.
- ^ ab Pontius, Robert; Millones, Marco (2011). "Muerte a Kappa: nacimiento del desacuerdo cuantitativo y el desacuerdo en la asignación para la evaluación de la precisión". Revista Internacional de Teledetección . 32 (15): 4407–4429. Bibcode :2011IJRS...32.4407P. doi :10.1080/01431161.2011.552923. S2CID 62883674.
- ^ Galton, F. (1892) Huellas dactilares Macmillan, Londres.
- ^ Smeeton, NC (1985). "Historia temprana de la estadística Kappa". Biometrics . 41 (3): 795. JSTOR 2531300.
- ^ Cohen, Jacob (1960). "Un coeficiente de acuerdo para escalas nominales". Medición educativa y psicológica . 20 (1): 37–46. doi :10.1177/001316446002000104. hdl : 1942/28116 . S2CID 15926286.
- ^ Sim, Julius; Wright, Chris C. (2005). "El estadístico Kappa en estudios de fiabilidad: uso, interpretación y requisitos de tamaño de muestra". Fisioterapia . 85 (3): 257–268. doi : 10.1093/ptj/85.3.257 . ISSN 1538-6724. PMID 15733050.
- ^ Chicco D.; Warrens MJ; Jurman G. (junio de 2021). "El coeficiente de correlación de Matthews (MCC) es más informativo que la puntuación Kappa y Brier de Cohen en la evaluación de la clasificación binaria". IEEE Access . 9 : 78368 - 78381. Bibcode :2021IEEEA...978368C. doi : 10.1109/ACCESS.2021.3084050 . hdl : 10281/430460 .
- ^ Heidke, P. (1 de diciembre de 1926). "Berechnung Des Erfolges Und Der Güte Der Windstärkevorhersagen Im Sturmwarnungsdienst". Geografiska Annaler . 8 (4): 301–349. doi :10.1080/20014422.1926.11881138. ISSN 2001-4422.
- ^ Sociedad Filosófica de Washington (Washington, DC) (1887). Boletín de la Sociedad Filosófica de Washington. Vol. 10. Washington, DC: Publicado con la colaboración del Instituto Smithsoniano. pág. 83.
- ^ Kilem Gwet (mayo de 2002). «Confiabilidad entre evaluadores: dependencia de la prevalencia de rasgos y homogeneidad marginal» (PDF) . Métodos estadísticos para la evaluación de la confiabilidad entre evaluadores . 2 : 1–10. Archivado desde el original (PDF) el 7 de julio de 2011. Consultado el 2 de febrero de 2011 .
- ^ ab Bakeman, R.; Gottman, JM (1997). Observación de la interacción: una introducción al análisis secuencial (2.ª ed.). Cambridge, Reino Unido: Cambridge University Press. ISBN 978-0-521-27593-4.
- ^ Fleiss, JL; Cohen, J.; Everitt, BS (1969). "Errores estándar de kappa y kappa ponderado en muestras grandes". Psychological Bulletin . 72 (5): 323–327. doi :10.1037/h0028106.
- ^ Robinson, BF; Bakeman, R. (1998). "ComKappa: Un programa de Windows 95 para calcular kappa y estadísticas relacionadas". Métodos, instrumentos y computadoras de investigación del comportamiento . 30 (4): 731–732. doi : 10.3758/BF03209495 .
- ^ Sim, J; Wright, C. C (2005). "El estadístico Kappa en estudios de fiabilidad: uso, interpretación y requisitos de tamaño de muestra". Fisioterapia . 85 (3): 257–268. doi : 10.1093/ptj/85.3.257 . PMID 15733050.
- ^ Bakeman, R.; Quera, V.; McArthur, D.; Robinson, BF (1997). "Detección de patrones secuenciales y determinación de su fiabilidad con observadores falibles". Psychological Methods . 2 (4): 357–370. doi :10.1037/1082-989X.2.4.357.
- ^ Landis, JR; Koch, GG (1977). "La medición del acuerdo entre observadores para datos categóricos". Biometrics . 33 (1): 159–174. doi :10.2307/2529310. JSTOR 2529310. PMID 843571. S2CID 11077516.
- ^ Gwet, K. (2010). "Manual de confiabilidad entre evaluadores (segunda edición)" ISBN 978-0-9708062-2-2 [ página necesaria ]
- ^ Fleiss, JL (1981). Métodos estadísticos para tasas y proporciones (2.ª ed.). Nueva York: John Wiley. ISBN 978-0-471-26370-8.
- ^ Umesh, UN; Peterson, RA; Sauber MH (1989). "Acuerdo entre jueces y el valor máximo de kappa". Medición educativa y psicológica . 49 (4): 835–850. doi :10.1177/001316448904900407. S2CID 123306239.
- ^ Viera, Anthony J.; Garrett, Joanne M. (2005). "Entender la concordancia entre observadores: la estadística kappa". Medicina familiar . 37 (5): 360–363. PMID 15883903.
- ^ Strijbos, J.; Martens, R.; Prins, F.; Jochems, W. (2006). "Análisis de contenido: ¿de qué están hablando?". Computers & Education . 46 : 29–48. CiteSeerX 10.1.1.397.5780 . doi :10.1016/j.compedu.2005.04.002. S2CID 14183447.
- ^ Uebersax, JS. (1987). "Diversidad de modelos de toma de decisiones y medición del acuerdo entre evaluadores" (PDF) . Psychological Bulletin . 101 : 140–146. CiteSeerX 10.1.1.498.4965 . doi :10.1037/0033-2909.101.1.140. S2CID 39240770. Archivado desde el original (PDF) el 2016-03-03 . Consultado el 2010-10-16 .
- ^ Delgado, Rosario; Tibau, Xavier-Andoni (2019-09-26). "Por qué se debe evitar el índice Kappa de Cohen como medida de desempeño en la clasificación". PLOS ONE . 14 (9): e0222916. Bibcode :2019PLoSO..1422916D. doi : 10.1371/journal.pone.0222916 . ISSN 1932-6203. PMC 6762152 . PMID 31557204.
- ^ Powers, David MW (2012). "El problema con Kappa" (PDF) . Conferencia del Capítulo Europeo de la Asociación de Lingüística Computacional (EACL2012) Taller conjunto ROBUS-UNSUP . Archivado desde el original (PDF) el 2016-05-18 . Consultado el 2012-07-20 .
- ^ Cohen, J. (1968). "Kappa ponderado: acuerdo de escala nominal con previsión de desacuerdo escalonado o crédito parcial". Psychological Bulletin . 70 (4): 213–220. doi :10.1037/h0026256. PMID 19673146.


































