Fuerza de marea

La fuerza de marea o fuerza generadora de marea es un efecto gravitacional que estira un cuerpo a lo largo de la línea hacia y desde el centro de masa de otro cuerpo debido a las variaciones espaciales en la fuerza del campo gravitacional del otro cuerpo. Es responsable de las mareas y fenómenos relacionados, incluidas las mareas de tierra sólida , el bloqueo de mareas , la ruptura de cuerpos celestes y la formación de sistemas de anillos dentro del límite de Roche y, en casos extremos, la espaguetificación de objetos. Surge porque el campo gravitacional ejercido sobre un cuerpo por otro no es constante en todas sus partes: el lado más cercano es atraído con más fuerza que el lado más lejano. La diferencia es positiva en el lado cercano y negativa en el lado lejano, lo que hace que un cuerpo se estire. Por lo tanto, la fuerza de marea también se conoce como fuerza diferencial, fuerza residual o efecto secundario del campo gravitacional.
En mecánica celeste , la expresión fuerza de marea puede referirse a una situación en la que un cuerpo o material (por ejemplo, el agua de marea) está principalmente bajo la influencia gravitatoria de un segundo cuerpo (por ejemplo, la Tierra), pero también es perturbado por los efectos gravitatorios de un tercer cuerpo (por ejemplo, la Luna). La fuerza perturbadora a veces se denomina en tales casos fuerza de marea [2] (por ejemplo, la fuerza perturbadora sobre la Luna ): es la diferencia entre la fuerza ejercida por el tercer cuerpo sobre el segundo y la fuerza ejercida por el tercer cuerpo sobre el primero. [3]
También se ha demostrado que las fuerzas de marea están fundamentalmente relacionadas con las ondas gravitacionales . [4]
Explicación
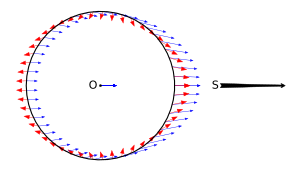
La rotación de la Tierra explica además la aparición de dos mareas altas por día en el mismo lugar. En esta figura, la Tierra es el círculo negro central, mientras que la Luna está muy a la derecha. Muestra tanto el campo de mareas (flechas rojas gruesas) como el campo de gravedad (flechas azules delgadas) ejercidos sobre la superficie y el centro de la Tierra (etiqueta O) por la Luna (etiqueta S). La dirección hacia afuera de las flechas a la derecha y a la izquierda de la Tierra indica dónde está la Luna en el cenit o en el nadir .
Cuando un cuerpo (cuerpo 1) es sometido a la acción de la gravedad de otro cuerpo (cuerpo 2), el campo puede variar significativamente en el cuerpo 1 entre el lado del cuerpo que mira hacia el cuerpo 2 y el lado que mira en dirección opuesta al cuerpo 2. La figura 2 muestra la fuerza diferencial de la gravedad sobre un cuerpo esférico (cuerpo 1) ejercida por otro cuerpo (cuerpo 2).
Estas fuerzas de marea provocan tensiones en ambos cuerpos y pueden distorsionarlos o incluso, en casos extremos, romper uno u otro. [5] El límite de Roche es la distancia a un planeta a la que los efectos de las mareas causarían la desintegración de un objeto porque la fuerza diferencial de gravedad del planeta supera la atracción de las partes del objeto entre sí. [6] Estas tensiones no ocurrirían si el campo gravitatorio fuera uniforme, porque un campo uniforme solo hace que todo el cuerpo se acelere en conjunto en la misma dirección y a la misma velocidad.
Tamaño y distancia
La relación entre el tamaño de un cuerpo astronómico y su distancia a otro cuerpo influye fuertemente en la magnitud de la fuerza de marea. [7] La fuerza de marea que actúa sobre un cuerpo astronómico, como la Tierra, es directamente proporcional al diámetro de la Tierra e inversamente proporcional al cubo de la distancia a otro cuerpo que produce atracción gravitatoria, como la Luna o el Sol. La acción de las mareas sobre bañeras, piscinas, lagos y otros pequeños cuerpos de agua es insignificante. [8]
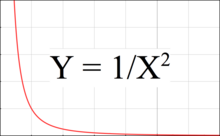
La figura 3 es un gráfico que muestra cómo la fuerza gravitacional disminuye con la distancia. En este gráfico, la fuerza de atracción disminuye en proporción al cuadrado de la distancia ( Y = 1/ X 2 ), mientras que la pendiente ( Y ′ = −2/ X 3 ) es inversamente proporcional al cubo de la distancia.
La fuerza de marea corresponde a la diferencia en Y entre dos puntos del gráfico, uno de ellos en el lado cercano del cuerpo y el otro en el lado lejano. La fuerza de marea aumenta cuando los dos puntos están más separados o cuando están más a la izquierda en el gráfico, es decir, más cerca del cuerpo que los atrae.
Por ejemplo, aunque el Sol tiene una mayor atracción gravitatoria en general sobre la Tierra, la Luna crea un abultamiento de marea más grande porque la Luna está más cerca. Esta diferencia se debe a la forma en que la gravedad se debilita con la distancia: la proximidad de la Luna crea una disminución más pronunciada en su atracción gravitatoria a medida que te mueves a través de la Tierra (en comparación con la disminución muy gradual del Sol desde su gran distancia). Este gradiente más pronunciado en la atracción de la Luna da como resultado una mayor diferencia de fuerza entre los lados cercano y lejano de la Tierra, que es lo que crea el abultamiento de marea más grande.
La atracción gravitatoria es inversamente proporcional al cuadrado de la distancia desde la fuente. La atracción será más fuerte en el lado del cuerpo que mira hacia la fuente y más débil en el lado que está más alejado de ella. La fuerza de marea es proporcional a la diferencia. [8]
Sol, Tierra y Luna
La Tierra es 81 veces más masiva que la Luna y su radio es aproximadamente cuatro veces mayor que el de la Luna. Por lo tanto, a la misma distancia, la fuerza de marea de la Tierra en la superficie de la Luna es aproximadamente 20 veces mayor que la de la Luna en la superficie de la Tierra. [9]
| Cuerpo gravitacional que provoca fuerza de marea | Cuerpo sometido a fuerza de marea | Aceleración de las mareas | |||
|---|---|---|---|---|---|
| Cuerpo | Masa ( ) | Cuerpo | Radio ( ) | Distancia ( ) | |
| Sol | 1,99 × 10 30 kilos | Tierra | 6,37 × 10 6 m | 1,50 × 10 11 m | 5,05 × 10 −7 m⋅s −2 |
| Luna | 7,34 × 10 22 kilogramos | Tierra | 6,37 × 10 6 m | 3,84 × 10 8 m | 1,10 × 10 −6 m⋅s −2 |
| Tierra | 5,97 × 10 24 kilos | Luna | 1,74 × 10 6 m | 3,84 × 10 8 m | 2,44 × 10 −5 m⋅s −2 |
| G es la constante gravitacional =6,674 × 10 −11 m 3 ⋅ kg −1 ⋅ s −2 [ 10] | |||||
Efectos

En el caso de una esfera elástica infinitesimalmente pequeña, el efecto de una fuerza de marea es distorsionar la forma del cuerpo sin ningún cambio en el volumen. La esfera se convierte en un elipsoide con dos protuberancias, que apuntan hacia y desde el otro cuerpo. Los objetos más grandes se distorsionan en un ovoide y se comprimen ligeramente, que es lo que sucede con los océanos de la Tierra bajo la acción de la Luna. Todas las partes de la Tierra están sujetas a las fuerzas gravitacionales de la Luna, lo que hace que el agua de los océanos se redistribuya, formando protuberancias en los lados cercanos a la Luna y alejados de ella. [12]
Cuando un cuerpo gira mientras está sujeto a fuerzas de marea, la fricción interna produce una disipación gradual de su energía cinética rotacional en forma de calor. En el caso de la Tierra y la Luna de la Tierra, la pérdida de energía cinética rotacional produce una ganancia de aproximadamente 2 milisegundos por siglo. Si el cuerpo está lo suficientemente cerca de su cuerpo primario, esto puede producir una rotación que está bloqueada por las mareas con el movimiento orbital, como en el caso de la luna de la Tierra. El calentamiento por marea produce efectos volcánicos dramáticos en la luna de Júpiter, Ío .Las tensiones causadas por las fuerzas de marea también causan un patrón mensual regular de terremotos lunares en la Luna de la Tierra. [7]
Las fuerzas de marea contribuyen a las corrientes oceánicas, que moderan las temperaturas globales al transportar energía térmica hacia los polos. Se ha sugerido que las variaciones en las fuerzas de marea se correlacionan con períodos fríos en el registro de temperatura global en intervalos de 6 a 10 años [13] y que las variaciones armónicas en la fuerza de marea pueden contribuir a los cambios climáticos milenarios. Hasta la fecha, no se ha encontrado un vínculo sólido con los cambios climáticos milenarios [14] .

Los efectos de las mareas se hacen particularmente pronunciados cerca de cuerpos pequeños de gran masa, como estrellas de neutrones o agujeros negros , donde son responsables de la " espaguetificación " de la materia que cae sobre ellos. Las fuerzas de marea crean la marea oceánica de los océanos de la Tierra , donde los cuerpos que atraen son la Luna y, en menor medida, el Sol . Las fuerzas de marea también son responsables del bloqueo de mareas , la aceleración de mareas y el calentamiento de mareas. Las mareas también pueden inducir sismicidad .
Al generar fluidos conductores dentro del interior de la Tierra, las fuerzas de marea también afectan el campo magnético de la Tierra . [15]
Formulación

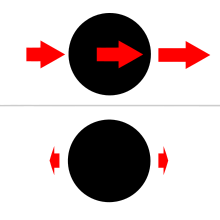
Para un campo gravitatorio dado (generado externamente), la aceleración de marea en un punto con respecto a un cuerpo se obtiene por sustracción vectorial de la aceleración gravitatoria en el centro del cuerpo (debida al campo generado externamente dado) de la aceleración gravitatoria (debida al mismo campo) en el punto dado. En consecuencia, el término fuerza de marea se utiliza para describir las fuerzas debidas a la aceleración de marea. Obsérvese que para estos fines, el único campo gravitatorio considerado es el externo; el campo gravitatorio del cuerpo (como se muestra en el gráfico) no es relevante. (En otras palabras, la comparación se realiza con las condiciones en el punto dado tal como serían si no hubiera un campo generado externamente que actuara de manera desigual en el punto dado y en el centro del cuerpo de referencia. El campo generado externamente suele ser el producido por un tercer cuerpo perturbador, a menudo el Sol o la Luna en los frecuentes casos de ejemplo de puntos sobre o por encima de la superficie de la Tierra en un marco de referencia geocéntrico).
La aceleración de las mareas no requiere rotación ni cuerpos en órbita; por ejemplo, el cuerpo puede estar cayendo libremente en línea recta bajo la influencia de un campo gravitacional y al mismo tiempo estar influenciado por la aceleración de las mareas (cambiante).
Según la ley de gravitación universal de Newton y las leyes del movimiento, un cuerpo de masa m a una distancia R del centro de una esfera de masa M siente una fuerza ,
equivalente a una aceleración ,
donde es un vector unitario que apunta desde el cuerpo M al cuerpo m (aquí, la aceleración de m hacia M tiene signo negativo).
Consideremos ahora la aceleración debida a la esfera de masa M experimentada por una partícula en la vecindad del cuerpo de masa m . Con R como la distancia desde el centro de M al centro de m , sea ∆ r la distancia (relativamente pequeña) de la partícula desde el centro del cuerpo de masa m . Para simplificar, las distancias se consideran primero solo en la dirección que apunta hacia o desde la esfera de masa M . Si el cuerpo de masa m es en sí mismo una esfera de radio ∆ r , entonces la nueva partícula considerada puede estar ubicada en su superficie, a una distancia ( R ± ∆r ) desde el centro de la esfera de masa M , y ∆r puede tomarse como positivo donde la distancia de la partícula desde M es mayor que R . Dejando de lado cualquier aceleración gravitacional que pueda experimentar la partícula hacia m debido a la propia masa de m , tenemos la aceleración sobre la partícula debido a la fuerza gravitacional hacia M como:
Sacando el término R 2 del denominador obtenemos:
La serie de Maclaurin de es la que da una expansión en serie de:
El primer término es la aceleración gravitatoria debida a M en el centro del cuerpo de referencia , es decir, en el punto donde es cero. Este término no afecta a la aceleración observada de las partículas en la superficie de m porque con respecto a M , m (y todo lo que se encuentra en su superficie) está en caída libre. Cuando la fuerza sobre la partícula lejana se resta de la fuerza sobre la partícula cercana, este primer término se cancela, al igual que todos los demás términos de orden par. Los términos restantes (residuales) representan la diferencia mencionada anteriormente y son términos de fuerza de marea (aceleración). Cuando ∆ r es pequeño en comparación con R , los términos después del primer término residual son muy pequeños y se pueden descuidar, lo que da la aceleración de marea aproximada para las distancias ∆ r consideradas, a lo largo del eje que une los centros de m y M :
Cuando se calcula de esta manera para el caso donde ∆ r es una distancia a lo largo del eje que une los centros de m y M , se dirige hacia afuera desde el centro de m (donde ∆ r es cero).
Las aceleraciones de marea también se pueden calcular a partir del eje que une los cuerpos m y M , lo que requiere un cálculo vectorial . En el plano perpendicular a ese eje, la aceleración de marea se dirige hacia adentro (hacia el centro donde ∆ r es cero) y su magnitud es una aproximación lineal como en la Figura 2.
Las aceleraciones de marea en las superficies de los planetas del Sistema Solar son generalmente muy pequeñas. Por ejemplo, la aceleración de marea lunar en la superficie de la Tierra a lo largo del eje Luna-Tierra es de aproximadamente1,1 × 10 −7 g , mientras que la aceleración de las mareas solares en la superficie de la Tierra a lo largo del eje Sol-Tierra es de aproximadamente0,52 × 10 −7 g , donde g es la aceleración gravitacional en la superficie de la Tierra. Por lo tanto, la fuerza de elevación de las mareas (aceleración) debida al Sol es aproximadamente el 45% de la debida a la Luna. [17] La aceleración de las mareas solares en la superficie de la Tierra fue dada por primera vez por Newton en los Principia . [18]
Véase también
- Punto anfidrómico
- Planeta perturbado
- Marea galáctica
- Resonancia de marea
- Despojo por mareas
- Tensor de marea
- Curvatura del espacio-tiempo
Referencias
- ^ "El Hubble observa una interacción cósmica". nasa.gov . NASA. 11 de febrero de 2022 . Consultado el 9 de julio de 2022 .
- ^ "Sobre la fuerza de las mareas", IN Avsiuk, en "Cartas de astronomía soviética", vol. 3 (1977), págs. 96-99.
- ^ Véase p. 509 en "Astronomía: una perspectiva física", ML Kutner (2003).
- ^ arXiv, Tecnología emergente de (14 de diciembre de 2019). "Las fuerzas de marea llevan la firma matemática de las ondas gravitacionales". MIT Technology Review . Consultado el 12 de noviembre de 2023 .
- ^ R Penrose (1999). La nueva mente del emperador: sobre computadoras, mentes y leyes de la física . Oxford University Press . pág. 264. ISBN. 978-0-19-286198-6.
fuerza de marea.
- ^ Teresa Encrenaz ; J-P Bibring; M Blanc (2003). El Sistema Solar. Saltador. pag. 16.ISBN 978-3-540-00241-3.
- ^ ab "La fuerza de las mareas | Neil deGrasse Tyson". www.haydenplanetarium.org . Consultado el 10 de octubre de 2016 .
- ^ ab Sawicki, Mikolaj (1999). "Mitos sobre la gravedad y las mareas". El profesor de física . 37 (7): 438–441. Bibcode :1999PhTea..37..438S. CiteSeerX 10.1.1.695.8981 . doi :10.1119/1.880345. ISSN 0031-921X.
- ^ Schutz, Bernard (2003). Gravedad desde cero: una guía introductoria a la gravedad y la relatividad general (edición ilustrada). Cambridge University Press. pág. 45. ISBN 978-0-521-45506-0.Extracto de la página 45
- ^ "Valor CODATA 2022: constante de gravitación newtoniana". Referencia del NIST sobre constantes, unidades e incertidumbre . NIST . Mayo de 2024. Consultado el 18 de mayo de 2024 .
- ^ RS MacKay; JD Meiss (1987). Sistemas dinámicos hamiltonianos: una selección de reimpresiones. CRC Press . p. 36. ISBN 978-0-85274-205-1.
- ^ Rollin A Harris (1920). La enciclopedia americana: una biblioteca de conocimiento universal. Vol. 26. Encyclopedia Americana Corp. págs. 611–617.
- ^ Keeling, CD; Whorf, TP (5 de agosto de 1997). "Posible forzamiento de la temperatura global por las mareas oceánicas". Actas de la Academia Nacional de Ciencias . 94 (16): 8321–8328. Bibcode :1997PNAS...94.8321K. doi : 10.1073/pnas.94.16.8321 . PMC 33744 . PMID 11607740.
- ^ Munk, Walter; Dzieciuch, Matthew; Jayne, Steven (febrero de 2002). "Variabilidad climática milenaria: ¿existe una conexión con las mareas?". Journal of Climate . 15 (4): 370–385. Bibcode :2002JCli...15..370M. doi : 10.1175/1520-0442(2002)015<0370:MCVITA>2.0.CO;2 .
- ^ "Hambrientos de poder en el espacio". New Scientist . 123 : 52. 23 de septiembre de 1989 . Consultado el 14 de marzo de 2016 .
- ^ "Gemelos galácticos inseparables". Imagen de la semana de la ESA/Hubble . Consultado el 12 de julio de 2013 .
- ^ El Almirantazgo (1987). Manual de navegación del Almirantazgo. Vol. 1. The Stationery Office . pág. 277. ISBN 978-0-11-772880-6., Capítulo 11, pág. 277
- ^ Newton, Isaac (1729). Los principios matemáticos de la filosofía natural. Vol. 2. pág. 307. ISBN 978-0-11-772880-6.Newton estimó la fuerza para deprimir el mar en lugares distantes 90 grados del Sol en "1 a 38604600" (en términos de g ), y escribió que la fuerza para elevar el mar a lo largo del eje Sol-Tierra es "el doble de grande" (es decir, 2 a 38604600), lo que equivale aproximadamente a 0,52 × 10 −7 g, como se expresa en el texto.
Enlaces externos
- Análisis y predicción de mareas: GeoTide
- Mareas gravitacionales por J. Christopher Mihos de la Universidad Case Western Reserve
- Audio: Caín/Gay – Astronomy Cast Tidal Forces – Julio de 2007.
- Gray, Meghan; Merrifield, Michael. "Tidal Forces". Sesenta símbolos . Brady Haran para la Universidad de Nottingham .
- Pau Amaro Seoane. «Colisiones estelares: Disrupción de una estrella por efecto de marea de un agujero negro masivo» . Consultado el 28 de diciembre de 2018 .
- Mitos sobre la gravedad y las mareas por Mikolaj Sawicki del John A. Logan College y la Universidad de Colorado.
- Conceptos erróneos sobre las mareas por Donald E. Simanek
- Mareas y fuerza centrífuga de Paolo Sirtoli


















