Intensidad de la señal en las telecomunicaciones

En telecomunicaciones , ^[1] particularmente en ingeniería de radiofrecuencia , la intensidad de la señal se refiere a la potencia de salida del transmisor recibida por una antena de referencia a una distancia de la antena transmisora. Las transmisiones de alta potencia , como las utilizadas en radiodifusión , se expresan en dB - milivoltios por metro (dBmV/m). Para sistemas de muy baja potencia, como los teléfonos móviles , la intensidad de la señal suele expresarse en dB - microvoltios por metro (dBμV/m) o en decibelios por encima de un nivel de referencia de un milivatio ( dBm ). En la terminología de radiodifusión, 1 mV/m es 1000 μV/m o 60 dBμ (a menudo escrito dBu).

Ejemplos

• 100 dBμ o 100 mV/m: pueden producirse interferencias de cobertura en algunos receptores
• 60 dBμ o 1,0 mV/m: frecuentemente considerado el límite del área protegida de una estación de radio en América del Norte
• 40 dBμ o 0,1 mV/m: la intensidad mínima con la que se puede recibir una estación con una calidad aceptable en la mayoría de los receptores

La intensidad del campo eléctrico en un punto específico se puede determinar a partir de la potencia entregada a la antena transmisora, su geometría y la resistencia a la radiación. Consideremos el caso de una antena dipolo de media onda con alimentación central en el espacio libre , donde la longitud total L es igual a la mitad de la longitud de onda (λ/2). Si se construye a partir de conductores delgados, la distribución de corriente es esencialmente sinusoidal y el campo eléctrico radiante viene dado por

${\displaystyle E_{\theta }(r)={-jI_{\circ } \sobre 2\pi \varepsilon _{0}c\,r}{\cos \left(\scriptstyle {\pi \sobre 2}\cos \theta \right) \sobre \sin \theta }e^{j\left(\omega t-kr\right)}}$

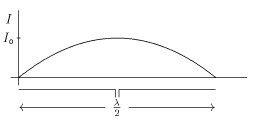
donde es el ángulo entre el eje de la antena y el vector al punto de observación, es la corriente pico en el punto de alimentación, es la permitividad del espacio libre, es la velocidad de la luz en el vacío y es la distancia a la antena en metros. Cuando la antena se ve de lado ( ) el campo eléctrico es máximo y está dado por ${\displaystyle \scriptstyle {\theta}}$${\displaystyle \scriptstyle {I_{\circ }}}$${\displaystyle \scriptstyle {\varepsilon _{0}\,=\,8,85\times 10^{-12}\,F/m}}$${\displaystyle \scriptstyle {c\,=\,3\times 10^{8}\,m/s}}$${\estilo de visualización \estilo de script {r}}$${\displaystyle \scriptstyle {\theta \,=\,\pi /2}}$

${\displaystyle \vert E_{\pi /2}(r)\vert ={I_{\circ } \sobre 2\pi \varepsilon _{0}c\,r}\,.}$

Resolviendo esta fórmula para la corriente pico obtenemos

${\displaystyle I_{\circ }=2\pi \varepsilon _{0}c\,r\vert E_{\pi /2}(r)\vert \,.}$

La potencia media de la antena es

${\displaystyle {P_{avg}={1 \sobre 2}R_{a}\,I_{\circ }^{2}}}$

donde es la resistencia de radiación de la antena de media onda alimentada por el centro. Sustituyendo la fórmula para en la fórmula para y despejando el campo eléctrico máximo se obtiene${\displaystyle \scriptstyle {R_{a}=73,13\,\Omega}}$${\displaystyle \scriptstyle {I_{\circ }}}$${\displaystyle \scriptstyle {P_{promedio}}}$

${\displaystyle \vert E_{\pi /2}(r)\vert \,=\,{1 \over \pi \varepsilon _{0}c\,r}{\sqrt {P_{avg} \over 2R_ {a}}}\,=\,{9.91 \sobre r}{\sqrt {P_{avg}}}\quad (L=\lambda /2)\,.}$

Por lo tanto, si la potencia promedio de una antena dipolo de media onda es 1 mW, entonces el campo eléctrico máximo a 313 m (1027 pies) es 1 mV/m (60 dBμ).

Para un dipolo corto ( ) la distribución de corriente es casi triangular. En este caso, el campo eléctrico y la resistencia de radiación son${\displaystyle \scriptstyle {L\ll \lambda /2}}$

${\displaystyle E_{\theta}(r)={-jI_{\circ}\sin(\theta ) \sobre 4\varepsilon _{0}c\,r}\left({L \sobre \lambda }\right)e^{j\left(\omega t-kr\right)}\,,\quad R_{a}=20\pi ^{2}\left({L \sobre \lambda }\right)^{2}.}$

Utilizando un procedimiento similar al anterior, el campo eléctrico máximo para un dipolo corto alimentado centralmente es

${\displaystyle \vert E_{\pi /2}(r)\vert \,=\,{1 \over \pi \varepsilon _{0}c\,r}{\sqrt {P_{avg} \over 160 }}\,=\,{9.48 \over r}{\sqrt {P_{avg}}}\quad (L\ll \lambda /2)\,.}$

Aunque existen redes de torres de estaciones base de telefonía celular en muchos países del mundo, todavía hay muchas áreas dentro de esos países que no tienen buena recepción. Es poco probable que algunas áreas rurales tengan cobertura efectiva, ya que el costo de erigir una torre celular es demasiado alto para unos pocos clientes. Incluso en áreas con alta intensidad de señal, los sótanos y los interiores de edificios grandes suelen tener mala recepción.

La intensidad de la señal también puede ser débil debido a interferencias destructivas de las señales de torres locales en áreas urbanas o a los materiales de construcción utilizados en algunos edificios que causan una atenuación significativa de la intensidad de la señal. Los edificios grandes, como almacenes, hospitales y fábricas, a menudo no tienen señal utilizable a más de unos pocos metros de las paredes exteriores.

Esto es particularmente cierto para las redes que operan a mayor frecuencia , ya que éstas se atenúan más por los obstáculos que intervienen, aunque son capaces de utilizar la reflexión y la difracción para sortear los obstáculos.

La intensidad estimada de la señal recibida en una etiqueta RFID activa se puede calcular de la siguiente manera:

${\displaystyle \mathrm {dBm_{e}} =-43,0-40,0\ \log _{10}\left({\frac {r}{R}}\right)}$

En general, puedes tener en cuenta el exponente de pérdida de trayectoria : ^[2]

${\displaystyle \mathrm {dBm_{e}} =-43,0-10,0\ \gamma \ \log _{10}\left({\frac {r}{R}}\right)}$

La pérdida de trayectoria efectiva depende de la frecuencia , la topografía y las condiciones ambientales.

En realidad, se podría utilizar cualquier potencia de señal conocida dBm ₀ a cualquier distancia r ₀ como referencia:

${\displaystyle \mathrm {dBm_{e}} =\mathrm {dBm} _{0}-10,0\ \gamma \ \log _{10}\left({\frac {r}{r_{0}}}\right)}$

$Estilo de visualización: log _{10}(R/r)$daría una estimación del número de décadas, que coincide con una pérdida de trayectoria promedio de 40 dB/década.

Cuando medimos la distancia celular r y los pares de potencia recibida dBm _m , podemos estimar el radio celular medio de la siguiente manera:

${\displaystyle R_{e}=\operatorname {promedio} [\ r\ 10^{(\mathrm {dBm_{m}} +43.0)/40.0}\ ]}$

Existen modelos de cálculo especializados para planificar la ubicación de una nueva torre de telefonía celular, teniendo en cuenta las condiciones locales y los parámetros del equipo de radio , además de considerar que las señales de radio móvil tienen propagación en línea de visión , a menos que se produzca reflexión.

• Red celular
• Teléfono móvil
• Repetidor celular
• Llamada interrumpida
• Zona muerta (teléfono móvil)
• Intensidad de campo dipolar en el espacio libre
• Medidor de intensidad de campo
• Indicador de intensidad de la señal recibida
• Medidor S
• Señal
• Señal de teléfono móvil
• Cobertura móvil

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Signal strength in telecommunications" – news · newspapers · books · scholar · JSTOR (January 2017) (Learn how and when to remove this message)