Onda automática

Las ondas automáticas son ondas no lineales autosuficientes en medios activos (es decir, aquellas que proporcionan fuentes de energía distribuidas). El término se utiliza generalmente en procesos en los que las ondas transportan una energía relativamente baja, necesaria para la sincronización o conmutación del medio activo.

Introducción

Relevancia y trascendencia

Las autoondas (AW) son análogos distribuidos de la autooscilación observada en sistemas puntuales. Ejemplos de ellos son las ondas de combustión, los impulsos nerviosos, las ondas de transición de túnel de distribución (en semiconductores), etc. Los procesos de autoondas (AWP) subyacen a la mayoría de los procesos de gestión y transferencia de información en sistemas biológicos. (...) Una característica interesante de los medios activos es que las estructuras de autoondas (AWS) pueden ocurrir en ellos. (...) La importancia de este trabajo es la siguiente
1. Tanto las AW como las AWS pueden ocurrir en sistemas de cualquier naturaleza física, cuya dinámica se describe mediante las ecuaciones (1) .
2. Este es un nuevo tipo de procesos dinámicos que dan lugar a la escala lineal macroscópica a través de interacciones locales, cada una de las cuales no tiene una escala lineal
. 3. Las AWS dan la base de la morfogénesis en los organismos vivos (es decir, en los sistemas biológicos).
4. La aparición de AWS es un nuevo mecanismo de turbulencia en entornos activos.

Haga clic en " mostrar " para ver el texto original (en ruso)
Los automóviles (АВ) se utilizan en sistemas análogos. Их примерами являются волны горения, нервные импульсы, волны распределения туннельных переходов (в полупроводниках) и т.п. Los procesos automáticos (АВП) leen en los últimos procesos de actualización y consulta de información biológica sistemas. (...) Интересной особенностью активных сред является то, что в них могут возникать автоволновые структуры (АВС) (...) Важность АВС Определяется следующим:
1. АВ y АВС pueden utilizarse en sistemas de trabajo físico durante períodos dinámicos descripción уравнениями вида (1).
2. Este nuevo tipo de procesos dinámicos, que permiten una limpieza macroscópica de líneas locales взаимодействий, каждое из которых линейным масштабом не обладает.
3. АВС являются основой морфогенеза в биологических системах.
4. Возникновение АВС — nuevos mecanismos de turbulencia en aplicaciones activas.
—  (1981), [B: 1]

En 1980, los científicos soviéticos GR Ivanitsky, VI Krinsky, AN Zaikin, AM Zhabotinsky , [A: 1] [A: 2] [B: 2] BP Belousov se convirtieron en ganadores del premio estatal más alto de la URSS , el Premio Lenin " por el descubrimiento de una nueva clase de procesos de autoondas y el estudio de ellos en perturbaciones de la estabilidad de los sistemas excitables distribuidos ".

Una breve historia de las investigaciones sobre ondas automáticas

El primero que estudió activamente las autooscilaciones fue el académico AA Andronov , y el término " autooscilaciones " en la terminología rusa fue introducido por AA Andronov en 1928. Sus seguidores [nota 1] de la Universidad Lobachevsky contribuyeron en gran medida al desarrollo de la teoría de autoondas .

Las ecuaciones de autoondas más simples que describen los procesos de combustión fueron estudiadas por A. N. Kolmogorov , [A: 3] I. E. Petrovsky, N. S. Piskunov en 1937, así como por Ya. B. Zel'dovich y D. A. Frank-Kamenetski [A: 4] en 1938.

El modelo axiomático clásico con autoondas en el miocardio fue publicado en 1946 por Norbert Wiener y Arturo Rosenblueth . [A: 5]

En los años 1970-80, los principales esfuerzos para estudiar las autoondas se concentraron en el Instituto de Física Biológica de la Academia de Ciencias de la URSS , situado en la ciudad suburbana de Pushchino , cerca de Moscú. Fue aquí, bajo la dirección de VIKrinsky, donde se formaron y formaron expertos mundialmente famosos en el campo de las investigaciones sobre autoondas como AVPanfilov, IREfimov, RRAliev, KI Agladze, OAMornev, MATsyganov. VVBiktashev, Yu.E. Elkin, AV Moskalenko adquirieron su experiencia con la teoría de las autoondas también en Pushchino, en el vecino Instituto de Problemas Matemáticos de la Biología , bajo la dirección de EEShnoll.

El término "procesos de autoondas" para todos estos (y otros) fenómenos fue acuñado por el físico soviético R. V. Khokhlov. Existen relaciones claras e importantes entre estas autoondas y las ideas de la sinergética y la autoorganización.

—  VA Vasiliev et al. (1987), [B:3]

El término " autoondas " fue propuesto, probablemente, por analogía del término anterior " autooscilaciones ".

Casi inmediatamente después de la disolución de la Unión Soviética , muchos de estos científicos rusos abandonaron su país natal para trabajar en instituciones extranjeras, donde aún continúan sus estudios sobre las autoondas. En particular, EREfimov está desarrollando la teoría del electrodo virtual , [A: 6] que describe algunos efectos que ocurren durante la desfibrilación .

Entre otros científicos notables, que están involucrados en estas investigaciones, se encuentran AN Zaikin y EEShnoll (autoondas y memoria de bifurcación en el sistema de coagulación sanguínea); [A: 7] [A: 8] A.Yu. Loskutov (teoría general de autoondas así como caos dinámico en autoondas); [B: 4] VG Yakhno (teoría general de autoondas así como conexiones entre autoondas y proceso de pensamiento); [A: 9] KI Agladze (autoondas en medios químicos); [A: 10] [A: 11] VNBiktashev (teoría general de autoondas así como diferentes tipos de deriva de autoondas); [A: 12] [A: 13] OAMornev (teoría general de autoondas); [A: 14] [A: 15] MATsyganov (el papel de las autoondas en la dinámica de poblaciones); [A: 16] Yu.E. Elkin, AV Moskalenko, ( memoria de bifurcación en un modelo de tejido cardíaco). [A: 17] [A: 18]

Un papel importante en el estudio de los modelos de autoondas del tejido cardíaco pertenece a Denis Noble y a los miembros de su equipo de la Universidad de Oxford .

Las definiciones básicas

Una de las primeras definiciones de autoondas fue la siguiente:

En la actualidad se acepta considerar una autoonda como un proceso ondulatorio autosostenido en un entorno de no equilibrio que permanece inalterado ante cambios suficientemente pequeños tanto en las condiciones iniciales como en las de contorno. (...) Los aparatos matemáticos para describir las autoondas son a menudo las ecuaciones del tipo de difusión con una no linealidad activa .

Haga clic en " mostrar " para ver el texto original (en ruso)
Под автоволнами принято сейчас понимать самоподдерживающийся волновой процесс в неравновесной среде, остающийся неизменным ри достаточно малых изменениях как начальных, так и граничных условий. (...) El aparato matemático de operación del automóvil busca cualquier tipo de solución de difusión con una red activa.
—  (1981), [B: 1]

A diferencia de las ondas lineales, como las ondas sonoras, las ondas electromagnéticas y otras, que son inherentes a los sistemas conservativos y se describen matemáticamente mediante ecuaciones hiperbólicas lineales de segundo orden ( ecuaciones de onda ), la dinámica de una autoonda en términos de ecuaciones diferenciales se puede describir mediante una ecuación parabólica con un miembro libre no lineal de una forma especial .

La forma concreta del miembro libre es extremadamente importante, porque: F → ( tú → ) {\displaystyle {\vec {f}}({\vec {u}})}

...todos los procesos ondulatorios generados por la dinámica no lineal de un sistema puntual , que es autooscilante o potencialmente autooscilante. tú → ˙ = F → ( tú → ) {\displaystyle {\dot {\vec {u}}}={\vec {f}}({\vec {u}})}

Haga clic en " mostrar " para ver el texto original (en ruso)
все волновые процессы порождаются динамикой нелинейной точечной системы , которая является автоколебательной или потенциально автоколебательной. tú → ˙ = F → ( tú → ) {\displaystyle {\dot {\vec {u}}}={\vec {f}}({\vec {u}})}
—  (1981), [B: 1]

Comúnmente, tienen la forma de dependencia en forma de - de . [ aclaración necesaria ] En este sentido, el sistema de ecuaciones, conocido como el modelo de Aliev-Panfilov, [A: 19] es un ejemplo muy exótico, porque tiene en él una forma muy compleja de dos parábolas que se intersecan, además de más cruzadas con dos líneas rectas, lo que resulta en propiedades no lineales más pronunciadas de este modelo. F {\estilo de visualización f} norte {\estilo de visualización N} tú {\estilo de visualización u} F ( tú ) {\displaystyle f(u)}

Las autoondas son un ejemplo de un proceso ondulatorio autosostenido en sistemas no lineales extensos que contienen fuentes de energía distribuidas. Es correcto que en el caso de las autoondas simples, el período, la longitud de onda, la velocidad de propagación, la amplitud y algunas otras características de una autoonda estén determinadas únicamente por las propiedades locales del medio. Sin embargo, en el siglo XXI, los investigadores comenzaron a descubrir un número creciente de ejemplos de soluciones de autoondas cuando se viola el principio "clásico".

(Véase también información general en la literatura, por ejemplo, en [B: 5] [B: 3] [B: 6] [B: 4] [A: 20] [A: 17] [A: 18] [A: 7] [A: 8] ).

Los ejemplos más simples

Una solución de frente de onda conmutado para la ecuación de Fisher (ver Reacción-difusión para más detalles).

El modelo más simple de onda automática es una fila de fichas de dominó que van cayendo una tras otra, si se deja caer la más alejada (el llamado " efecto dominó "). Este es un ejemplo de una onda de conmutación .

Como otro ejemplo de autoondas, imaginemos que nos encontramos en un campo y prendemos fuego a la hierba. Mientras la temperatura esté por debajo del umbral, la hierba no se incendiará. Al alcanzar la temperatura umbral ( temperatura de autoignición ) comienza el proceso de combustión , con la liberación de calor suficiente para encender las zonas más cercanas. El resultado es que se ha formado el frente de combustión, que se extiende por el campo. Se puede decir en tales casos que surgió la autoonda, que es uno de los resultados de la autoorganización en sistemas termodinámicos de no equilibrio. Después de algún tiempo, la hierba nueva reemplaza a la quemada, y el campo adquiere de nuevo la capacidad de encenderse. Este es un ejemplo de una onda de excitación .

Hay una gran cantidad de otros objetos naturales que también se consideran entre los procesos de autoondas: reacciones químicas oscilatorias en medios activos (por ejemplo, la reacción de Belousov-Zhabotinsky ), la propagación de pulsos de excitación a lo largo de las fibras nerviosas, la señalización química de ondas en las colonias de ciertos microorganismos, las autoondas en películas ferroeléctricas y semiconductoras , las ondas de población, la propagación de epidemias y de genes , y muchos otros fenómenos.

Los impulsos nerviosos, que constituyen un ejemplo típico de autoondas en un medio activo con recuperación, fueron estudiados por Hermann von Helmholtz en 1850. Las propiedades de los impulsos nerviosos que son típicas de las soluciones de autoondas más simples (forma y amplitud universales, independientes de las condiciones iniciales, y aniquilación en caso de colisión) se determinaron en los años 1920 y 1930.

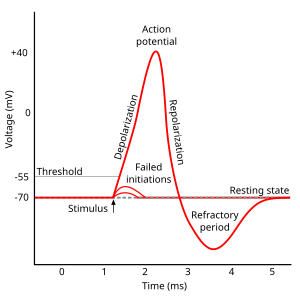
Esquema de un registro electrofisiológico de un potencial de acción que muestra las distintas fases que ocurren cuando la onda pasa por un punto en una membrana celular .

Consideremos un medio activo 2D formado por elementos, cada uno de los cuales se puede encontrar en tres estados diferentes: reposo, excitación y refractariedad . En ausencia de influencia externa, los elementos están en reposo. Como resultado de una influencia sobre él, cuando la concentración del activador alcanza el umbral, el elemento pasará a un estado excitado, adquiriendo la capacidad de excitar a los elementos vecinos. Algún tiempo después de la excitación, el elemento pasa a un estado refractario, en el que no puede ser excitado. Luego, el elemento vuelve a su estado inicial de reposo, ganando de nuevo la capacidad de transformarse en un estado excitado.

Cualquier onda de excitación "clásica" se mueve en un medio excitable sin atenuación, manteniendo su forma y amplitud constantes. A su paso, la pérdida de energía ( disipación ) se compensa completamente con la entrada de energía de los elementos del medio activo. El frente de avance de una autoonda (la transición del estado de reposo al de excitación) suele ser muy pequeño: por ejemplo, la relación entre la duración del frente de avance y la duración total del pulso de una muestra de miocardio es de aproximadamente 1:330.

Los métodos de modelado matemático por ordenador ofrecen posibilidades únicas para estudiar los procesos de autoondas en medios activos bidimensionales y tridimensionales con cinéticas muy diferentes. Para la simulación por ordenador de las autoondas se utiliza el modelo generalizado de Wiener-Rosenblueth, así como un gran número de otros modelos, entre los que ocupan un lugar especial el modelo de FitzHugh-Nagumo (el modelo más simple de un medio activo y sus diversas variantes) y el modelo de Hodgkin-Huxley (impulso nervioso). También existen muchos modelos de autoondas miocárdicas: el modelo de Beeler-Reuter, varios modelos de Noble (desarrollados por Denis Noble ), el modelo de Aliev-Panfilov, el modelo de Fenton-Karma, etc.

Propiedades básicas de las autoondas

También se demostró [A: 21] que los regímenes de ondas automáticas más simples deberían ser comunes a todo sistema de ecuaciones diferenciales de cualquier complejidad que describa un medio activo particular, porque dicho sistema puede simplificarse a dos ecuaciones diferenciales.

Principales objetos de ondas automáticas conocidos

En primer lugar, debemos observar que los elementos de los medios activos pueden ser, al menos, de tres tipos muy diferentes; estos son regímenes autoexcitados , excitables y de disparo (o biestables ). En consecuencia, existen tres tipos de medios activos homogéneos compuestos por estos elementos.

Un elemento biestable tiene dos estados estacionarios estables, entre los cuales se producen transiciones cuando la influencia externa supera un cierto umbral. En los medios de estos elementos, se generan ondas de conmutación que hacen que el medio pase de uno de sus estados al otro. Por ejemplo, un caso clásico de este tipo de ondas automáticas de conmutación (quizás, el fenómeno de ondas automáticas más simple) es la caída de fichas de dominó (el ejemplo ya dado). Otro ejemplo simple de un medio biestable es el papel que se quema: la onda de conmutación se propaga en forma de llama, haciendo que el papel pase del estado normal a sus cenizas.

Un elemento excitable tiene un único estado estacionario estable. Una influencia externa que supere un nivel umbral puede sacar a dicho elemento de su estado estacionario y realizar una evolución antes de que vuelva a su estado estacionario. Durante esta evolución, el elemento activo puede afectar a los elementos adyacentes y, a su vez, sacarlos también del estado estacionario. Como resultado, la onda de excitación se propaga en este medio. Esta es la forma más común de autoondas en medios biológicos, como el tejido nervioso o el miocardio.

Un elemento autooscilante no tiene estados estacionarios y continuamente realiza oscilaciones estables de una forma, amplitud y frecuencia fijas. La influencia externa puede alterar estas oscilaciones. Después de un tiempo de relajación, todas sus características, excepto la fase, vuelven a su valor estable, pero la fase puede cambiar. Como resultado, las ondas de fase se propagan en el medio de tales elementos. Tales ondas de fase se pueden observar en guirnaldas eléctricas o en ciertos medios químicos. Un ejemplo de un medio autooscilante es el nódulo SA en el corazón, en el que surgen impulsos de excitación espontáneamente.

En el esquema de fases del sistema básico de ecuaciones que describe el medio activo (véase la figura) se puede ver claramente que una diferencia significativa entre estos tres tipos de comportamiento de un medio activo se debe a la cantidad y la posición de sus puntos singulares. La forma de las autoondas observadas en la realidad puede ser muy similar entre sí y, por lo tanto, puede ser difícil evaluar el tipo de elemento solo por la forma del pulso de excitación.

Además, los fenómenos de autoondas, que pueden observarse e investigarse, dependen en gran medida de las peculiaridades geométricas y topológicas de un medio activo.

Ondas automáticas unidimensionales

Los casos unidimensionales incluyen la propagación de la autoonda en el cable y su propagación en el anillo, considerándose este último modo como un caso límite de una onda rotatoria en un medio activo bidimensional, mientras que el primer caso se considera como la propagación de la autoonda en el anillo con curvatura cero (es decir, con un radio infinito).

Ondas automáticas bidimensionales

Reverberador de ondas automáticas que se encuentra en el sistema de reacción-difusión de dos componentes del tipo Fitzhugh-Nagumo mencionado anteriormente .

Se conocen varias fuentes de autoondas en los medios activos bidimensionales. De esta manera, se distinguen al menos cinco tipos de reentrada, [nota 2] que son la onda en anillo , la onda espiral , el reverberador (es decir, el vórtice de autoondas bidimensional ) y la fibrilación . La literatura identifica dos tipos de fuentes de autoondas concéntricas en los medios activos 2D; estos son los marcapasos y los centros principales . Tanto los centros principales como los reverberadores son interesantes, porque no están ligados a la estructura del medio y pueden aparecer y desaparecer en sus diferentes partes. Las áreas de mayor automatización también pueden ser un ejemplo de fuentes de autoondas. Actualmente se conocen tres tipos diferentes de mayor automatización: [B: 7]

  1. automatismo inducido
  2. Automatismo de activación con mecanismo de posdespolarización temprana
  3. automatismo de disparo con mecanismo de postdespolarización tardía .

Además de 2D [A: 22] [A: 13]

Consulte también los detalles en el artículo sobre ondas automáticas rotativas, que puede aparecer como onda espiral o reverberador de ondas automáticas .

Se observaron fenómenos de memoria de bifurcación en el comportamiento del reverberador de ondas automáticas en el modelo de Aliev-Panfilov. [A: 17]

Autoondas tridimensionales

3D. [A: 23] [A: 12]

Ejemplos de procesos de autoondas en la naturaleza

Régimen de ebullición de autoondas

Ondas automáticas en soluciones químicas

Un ejemplo de una reacción química que, en determinadas circunstancias, puede producir una autoonda es la reacción de Belousov-Zhabotinsky . [A: 1] [A: 2] [B: 2] [B: 8] [A: 24]

Modelos de autoondas de tejidos biológicos

Modelos de ondas automáticas de la retina

Modelos de ondas automáticas de fibras nerviosas

El elemento principal de la página " Modelo Hodgkin-Huxley "

Modelos de ondas automáticas del miocardio

El modelo clásico de Wiener-Rosenblueth, [A: 5] que, en consecuencia, fue desarrollado por Norbert Wiener y Arturo Rosenblueth .

Entre otros ejemplos se encuentran los siguientes: FitxHue-Nagumo, el modelo Beeler-Reuter. [A: 22] [A: 25]

Está previsto que el artículo principal aparezca en la página especial "Modelos de autoondas del miocardio"

Ondas automáticas en el sistema de coagulación sanguínea

Ver referencias. [A: 7] [A: 8]

La población se comunica automáticamente

Las amebas colectivas Dictyostelium discoideum, con un suministro suficiente, viven como organismos unicelulares . Sin embargo, durante la inanición se arrastran juntas formando un organismo multicelular , que luego produce esporas que pueden sobrevivir en condiciones adversas. Se descubrió que el movimiento de las amebas está controlado por la distribución de una sustancia, el morfógeno AMPc , en el medio ambiente. Estas células de ameba sintetizan y acumulan las moléculas de AMPc y luego son capaces de "liberar" esta reserva en el medio ambiente, si la concentración de AMPc aumenta en él. La cantidad liberada de AMPc se difunde a través del medio ambiente y hace que las amebas celulares siguientes "entren en acción" arrojando su porción del morfógeno al exterior. Como resultado, una onda automática de alta concentración de AMPc se propaga a través del medio ambiente. Después del paso de la onda, las células "descargadas" comienzan a acumular de nuevo una nueva porción de AMPc, debido a la síntesis, y después de un tiempo son capaces de "entrar en acción" nuevamente. Así, la población de las amebas colectivas es un ejemplo típico del medio activo .

Haga clic en " mostrar " para ver el texto original (en ruso)
Las especies colectivas de Dictyostelium discoideum se encuentran en todas partes de organizaciones independientes. Однако при голодании они сползаются и образуют ru:Многоклеточный организм, который впоследствии даёт ru:sporы, способные пережить неблагоприятные условия. Por lo general , esta televisión de pantalla está mejorada según la naturaleza de la televisión . Las cuerdas se sintetizan y se insertan en varias moléculas de energía y se colocan en el interior y se eliminan en funcionamiento. среду, если концентрация цАМФ в ней повысилась. Освободившееся количество цАМФ распространяется за счёт дфузии по среде и заставляет следующие клетки амёб «сработать», выбросив свою порцию морфогена. В результате по среде распространяется автоволна — повышенная концентрация цАМФ. Después de realizar una nueva programación, las llaves se pueden quitar nuevamente para que no se sientan afectadas por el problema. цАМФ y по прошествии некоторого времени способны «срабатывать» вновь. Таким образом, популяция колективных амёб служит типичным примером активной среды.
—  Krinsky y Mikhailov, (1984) [B: 5]

Ejemplos de modelos basados ​​en individuos de ondas automáticas de población

Modelo de autómatas celulares determinista lógico basado en individuos de un ecosistema con una especie. El modelo demuestra un mecanismo de crecimiento poblacional en forma de S.
Modelo de autómatas celulares determinista lógico basado en individuos que muestra la competencia interespecífica por un único recurso limitado. Mecanismo de exclusión competitiva de una especie por otra.

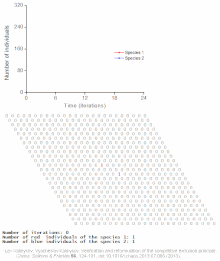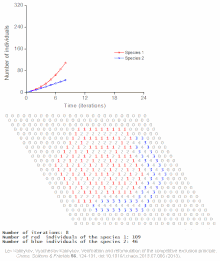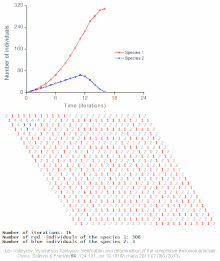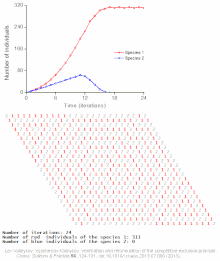
Véase también

Notas

  1. ^ Por ejemplo, la ciudadana honoraria de Nizhny Novgorod y científica honoraria de la RSFSR M. T. Grekhova fue la editora del libro "Procesos de autoondas en sistemas con difusión" (1981) — ver Referencias
  2. ^ Hoy en día se reconoce ampliamente el triste papel de la reentrada como causa de diversas arritmias cardíacas. El esquema básico de la reentrada se propuso ya en 1914, y se obtuvo en estudios de anillos de tejido cardíaco aislados (GR Mines — Trans.R.Soc.Can., 1914, 8, 43). T. Lewis, etc., demostró en 1921 que el aleteo auricular puede estar condicionado por la circulación de la onda de excitación por la aurícula derecha y por la izquierda (Heart, 1921, 8, 361). Este hecho fue confirmado nuevamente experimentalmente a mediados del siglo XX por CE Cabrera y D. Soli-Pollares (Arch. Inst. Cardiol. Mex., 1947, 17,850). En 1928, FOSchmidt y J. Erlanger (Am. J. Physiol. 1928-1929, 87, 326) sugirieron que la reentrada desempeña un papel esencial como mecanismo patogénico de la taquicardia supraventricular. También es responsable de muchos tipos de taquicardia ventricular y fibrilación ventricular.

Referencias

  • Libros
  1. ^ abc Грехова, М. Т., ed. (1981). Procesos automáticos en sistemas con problemas[ Procesos de Autowave en sistemas con difusión ] (en ruso). Горький: Институт прикладной математики АН СССР. pag. 287.
  2. ^ ab Жаботинский, А. M. Концентрационные автоколебания[ Autooscilaciones de concentración ] (en ruso). М.: Наука.
  3. ^ ab Vasiliev, VA; Romanovskii, Yu. M.; Chernavskii, DS; Yakhno, VG (1987). Procesos de autoondas en sistemas cinéticos. Autoorganización espacial y temporal en física, química, biología y medicina . Berlín: Springer Netherlands. doi :10.1007/978-94-009-3751-2. ISBN 978-94-010-8172-6.
  4. ^ ab Loskutov, A.; Mikhailov, AS (1995). Fundamentos de sinergética II. Patrones complejos . Berlín: Springer.
  5. ^ ab Кринский, В. И.; Михайлов, А. С. (1984). Automotrices[ Autowaves ] (en ruso). Moscú: Znanie.
  6. ^ Прохоров, А. М., ed. (1988). Enciclopedia física[ Enciclopedia de Física ] (en ruso). vol. 1. М.: Советская энциклопедия.
  7. ^ Елькин, Ю.Е.; Москаленко, А.В. (2009). "Базовые механизмы аритмий сердца" [Mecanismos básicos de las arritmias cardíacas]. En Ardashev, prof. AV (ed.). Клиническая аритмология [ Arritmología clínica ] (en ruso). Moscú: MedPraktika. pag. 1220.ISBN​ 978-5-98803-198-7.
  8. ^ Field, RJ; Burger, M., eds. (1985). Oscilaciones y ondas viajeras en sistemas químicos . John Wiley and Sons, Inc.
  • Papeles
  1. ^ ab Zaikin, AN; Zhabotinsky, AM (1970). "Propagación de ondas de concentración en un sistema autooscilante de fase líquida bidimensional". Nature . 225 (5232): 535–537. Bibcode :1970Natur.225..535Z. doi :10.1038/225535b0. PMID  16056595. S2CID  4178354.
  2. ^ ab Zhabotinsky, AM; Zaikin, AN (1973). "Procesos de autoondas en un sistema químico distribuido". Revista de biología teórica . 40 (1): 45–56. Bibcode :1973JThBi..40...45Z. doi :10.1016/0022-5193(73)90164-1. ISSN  0022-5193. PMID  4723554.
  3. ^ Kolmogorov, A.; et al. (1937). "Estudio de una ecuación de difusión relacionada con el crecimiento de una cualidad de materia y su aplicación a un problema biológico". Boletín de Matemáticas de la Universidad de Moscú . 1 : 1–26.
  4. ^ Zeldovich, YB; Frank-Kamenetski, DA (1938). "(artículo)". Acta Physicochimica URSS . 9 : 341–.
  5. ^ ab Wiener, N.; Rosenblueth, A. (1946). "La formulación matemática del problema de la conducción de impulsos en una red de elementos excitables conectados, específicamente en el músculo cardiaco". Archivos del Instituto de Cardiología de México . 16 (3–4): 205–265.
  6. ^ Sambelashvili, AT; Nikolski, VP; Efimov, IR (2004). "La teoría de electrodos virtuales explica el aumento del umbral de estimulación causado por daño tisular cardíaco". American Journal of Physiology. Fisiología cardíaca y circulatoria . 286 (6): H2183–H2194. doi :10.1152/ajpheart.00637.2003. PMID  14726298.
  7. ^ abc Ataullakhanov, FI; Zarnitsyn, VI; Kondratovich, A Yu; Lobanova, ES; Sarbash, VI (2002). "Una nueva clase de parada de ondas autosostenidas: un factor que determina la dinámica espacial de la coagulación sanguínea". Física-Uspekhi . 45 (6): 619–636. doi :10.3367/UFNr.0172.200206c.0671. ISSN  0042-1294.
  8. ^ abc Ataullakhanov, FI; Lobanova, ES; Morózova, OL; Shnol', EE; Ermakova, EA; Butilina, AA; Zaikin, AN (2007). "Regímenes intrincados de propagación de una excitación y autoorganización en el modelo de coagulación sanguínea". Física-Uspekhi . 50 : 79–94. doi :10.3367/UFNr.0177.200701d.0087. ISSN  0042-1294.
  9. ^ Vasil'ev, VA; Romanovskii, Yu M; Yakhno, VG (1979). "Procesos de autoondas en sistemas cinéticos distribuidos". Física-Uspekhi . 22 : 615–639. doi :10.3367/UFNr.0128.197908c.0625.
  10. ^ Agladze, KI; Krinsky, VI (1982). "Vórtices multibrazos en un medio químico activo". Nature . 296 (5856): 424–426. Código Bibliográfico :1982Natur.296..424A. doi :10.1038/296424a0. S2CID  4309561.
  11. ^ Agladze, KI; Krinsky, VI; Pertsov, AM (1984). "El caos en la reacción de Belousov-Zhabotinskii no agitada es inducido por la interacción de ondas y estructuras disipativas estacionarias". Nature . 308 (5962): 834–835. Bibcode :1984Natur.308..834A. doi :10.1038/308834a0. S2CID  4336506.
  12. ^ ab Biktashev, VN; Holden, AV; Zhang, H. (1994). "Tensión de los filamentos organizadores de las ondas de desplazamiento". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences . 347 (1685): 611–630. Bibcode :1994RSPTA.347..611B. doi :10.1098/rsta.1994.0070. S2CID  119470489.
  13. ^ ab Biktashev, VN; Holden, AV (1995). "Deriva resonante de vórtices de autoondas en dos dimensiones y el efecto de los límites y las inhomogeneidades". Caos, solitones y fractales . 5 (3–4): 575–622. Bibcode :1995CSF.....5..575B. doi :10.1016/0960-0779(93)E0044-C. ISSN  0960-0779.
  14. ^ Aslanidi, OV; Mornev, OA (1997). "¿Pueden reflejarse los pulsos nerviosos en colisión?". Journal of Experimental and Theoretical Physics Letters . 65 (7). Nauka/Interperiodica: 579–585. doi :10.1134/1.567398. ISSN  0021-3640.
  15. ^ Mornev, OA (2004). "Refracción de autoondas: regla de la tangente". Journal of Experimental and Theoretical Physics Letters . 80 (12). Nauka/Interperiodica: 721–724. doi :10.1134/1.1868793. ISSN  0021-3640.
  16. ^ Agladze, K.; Budrene, L.; Ivanitsky, G.; Krinsky, V.; Shakhbazyan, V.; Tsyganov, M. (1993). "Mecanismos de onda de formación de patrones en la población microbiana". Actas de la Royal Society B: Ciencias Biológicas . 253 (1337): 131–135. doi :10.1098/rspb.1993.0092. PMID  8397413. S2CID  838828.
  17. ^ abc Elkin, Yu. E.; Moskalenko, AV; Starmer, Ch.F. (2007). "Detención espontánea de la deriva de ondas espirales en medios excitables homogéneos". Biología matemática y bioinformática . 2 (1): 1–9. ISSN  1994-6538.
  18. ^ ab Moskalenko, AV; Elkin, Yu. E. (2009). "El lacet: un nuevo tipo de comportamiento de onda espiral". Caos, solitones y fractales . 40 (1): 426–431. Bibcode :2009CSF....40..426M. doi :10.1016/j.chaos.2007.07.081. ISSN  0960-0779.
  19. ^ Aliev, R.; Panfilov, A. (1996). "Un modelo simple de dos variables de la excitación cardíaca". Caos, solitones y fractales . 7 (3): 293–301. Bibcode :1996CSF.....7..293A. CiteSeerX 10.1.1.52.4271 . doi :10.1016/0960-0779(95)00089-5. ISSN  0960-0779. 
  20. ^ Елькин, Ю. Е. (2006). "Procesos de Autowave" Автоволновые процессы [Procesos de Autowave]. Математическая биология и биоинформатика (revista) (en ruso). 1 (1): 27–40. doi : 10.17537/2006.1.27 . ISSN  1994-6538.
  21. ^ Кринский, В. И.; Кокоз, Ю. M. (1973). "Анализ уравнений возбудимых мембран III. Мембрана волокна Пуркинье. Сведение уравнения Нобла к системе второго порядка. Анализ аномалии нуль-изоклин". Биофизика (revista) (en ruso). 18 (6): 1067–1073. ISSN  0006-3029.
  22. ^ ab Winfree, A. (1991). "Variedades del comportamiento de las ondas espirales: un enfoque experimentalista de la teoría de los medios excitables". Chaos . 1 (3): 303–334. Bibcode :1991Chaos...1..303W. doi :10.1063/1.165844. ISSN  1054-1500. PMID  12779929.
  23. ^ Keener, JP (1988). "La dinámica de ondas de desplazamiento tridimensionales en medios excitables". Physica D . 31 (2): 269–276. doi :10.1016/0167-2789(88)90080-2. ISSN  0167-2789.
  24. ^ Manelis, Georgii B; et al. (2012). "Procesos de autoondas en la combustión por filtración en sistemas de contraflujo". Russian Chemical Reviews . 81 (9): 855–. Código Bibliográfico :2012RuCRv..81R...4M. doi :10.1070/RC2012v081n09ABEH004279. ISSN  1468-4837. S2CID  96649671.
  25. ^ Efimov, IR; Krinsky, VI; Jalife, J. (1995). "Dinámica de vórtices rotatorios en el modelo Beeler-Reuter de tejido cardíaco". Caos, solitones y fractales . 5 (3/4): 513–526. Bibcode :1995CSF.....5..513E. doi : 10.1016/0960-0779(95)95761-F . ISSN  0960-0779.
  • Varios modelos clásicos simples de autowaves (JS + WebGL), que se pueden ejecutar directamente en su navegador web; desarrollado por Evgeny Demidov.
Obtenido de "https://es.wikipedia.org/w/index.php?title=Autowave&oldid=1245995639"