Icosaedro

En geometría , un icosaedro ( / ˌ aɪ k ɒ s ə ˈ h iː d r ən , - k ə -, - k oʊ -/ o / aɪ ˌ k ɒ s ə ˈ h iː d r ən / ^[1] ) es un poliedro de 20 caras. El nombre proviene del griego antiguo εἴκοσι (eíkosi)  'veinte' y ἕδρα (hédra)  'asiento'. El plural puede ser "icosaedros" ( /- d r ə / ) o "icosaedros".

Existen infinitas formas de icosaedros no semejantes , algunas de ellas más simétricas que otras. El más conocido es el icosaedro regular ( convexo , no estrellado ), uno de los sólidos platónicos , cuyas caras son 20 triángulos equiláteros .

Hay dos objetos, uno convexo y otro no convexo, que pueden llamarse icosaedros regulares. Cada uno tiene 30 aristas y 20 caras de triángulos equiláteros , cinco de las cuales se encuentran en cada uno de sus doce vértices. Ambos tienen simetría icosaédrica . El término "icosaedro regular" se refiere generalmente a la variedad convexa, mientras que la forma no convexa se denomina gran icosaedro .

El icosaedro regular convexo suele denominarse simplemente icosaedro regular , uno de los cinco sólidos platónicos regulares , y se representa mediante su símbolo Schläfli {3, 5}, que contiene 20 caras triangulares, con 5 caras que se encuentran alrededor de cada vértice.

Su poliedro dual es el dodecaedro regular {5, 3} que tiene tres caras pentagonales regulares alrededor de cada vértice.

El gran icosaedro es uno de los cuatro poliedros estelares regulares de Kepler-Poinsot . Su símbolo de Schläfli es {3, ⁠5/2⁠ }. Al igual que la forma convexa, también tiene 20 caras de triángulos equiláteros, pero su figura de vértice es un pentagrama en lugar de un pentágono, lo que da lugar a caras que se intersecan geométricamente. Las intersecciones de los triángulos no representan nuevas aristas.

Su poliedro dual es el gran dodecaedro estrellado { ⁠5/2⁠ , 3}, que tiene tres caras pentagonales estrelladas regulares alrededor de cada vértice.

La estelación es el proceso de extender las caras o aristas de un poliedro hasta que se juntan para formar un nuevo poliedro. Se realiza de manera simétrica para que la figura resultante conserve la simetría general de la figura original.

En su libro The Fifty-Nine Icosahedra , Coxeter et al. enumeraron 58 estelaciones de este tipo del icosaedro regular.

De ellos, muchos tienen una sola cara en cada uno de los 20 planos de caras y, por lo tanto, también son icosaedros. Entre ellos se encuentra el gran icosaedro.

Otras estelaciones tienen más de una cara en cada plano o forman compuestos de poliedros más simples. No son estrictamente icosaedros, aunque a menudo se los denomina como tales.

Estelaciones notables del icosaedro
Regular	Duelos uniformes			Compuestos regulares			Estrella regular	Otros
Icosaedro (convexo)	Icosaedro triámbico pequeño	Icosaedro triámbico medial	Gran icosaedro triámbico	Compuesto de cinco octaedros	Compuesto de cinco tetraedros	Compuesto de diez tetraedros	Gran icosaedro	Dodecaedro excavado	Estelación final
El proceso de estelación en el icosaedro crea una serie de poliedros y compuestos relacionados con simetría icosaédrica .

Simetrías piritoédricas y tetraédricas
Diagramas de Coxeter	(piritoédrico) (tetraédrico)
Símbolo de Schläfli	s{3,4} sr{3,3} o${\displaystyle s{\begin{Bmatrix}3\\3\end{Bmatrix}}}$
Caras	20 triángulos: 8 equiláteros y 12 isósceles
Bordes	30 (6 cortos + 24 largos)
Vértices	12
Grupo de simetría	T h , [4,3 + ], (3*2), orden 24
Grupo de rotación	T d , [3,3] + , (332), orden 12
Poliedro dual	Piritoedro
Propiedades	convexo
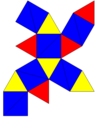
Neto
Un icosaedro regular es topológicamente idéntico a un cuboctaedro con sus 6 caras cuadradas bisecadas en diagonales con simetría piritoédrica. Existe una transformación cinemática entre cuboctaedro e icosaedro .

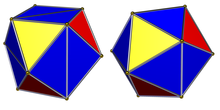
Un icosaedro regular puede distorsionarse o marcarse como una simetría piritoédrica inferior, ^{[2] [3]} y se denomina octaedro romo , tetratetraedro romo , tetraedro romo y pseudoicosaedro . ^[4] Esto puede verse como un octaedro truncado alternado . Si todos los triángulos son equiláteros , la simetría también se puede distinguir coloreando los conjuntos de 8 y 12 triángulos de manera diferente.

La simetría piritoédrica tiene el símbolo (3*2), [3 ⁺ ,4], con orden 24. La simetría tetraédrica tiene el símbolo (332), [3,3] ⁺ , con orden 12. Estas simetrías inferiores permiten distorsiones geométricas a partir de 20 caras triangulares equiláteras, teniendo en su lugar 8 triángulos equiláteros y 12 triángulos isósceles congruentes .

Estas simetrías ofrecen diagramas de Coxeter :yrespectivamente, cada uno representando la simetría inferior al icosaedro regular , (*532), [5,3] simetría icosaédrica de orden 120.

Las coordenadas cartesianas de los 12 vértices se pueden definir mediante los vectores definidos por todas las posibles permutaciones cíclicas y cambios de signo de coordenadas de la forma (2, 1, 0). Estas coordenadas representan el octaedro truncado con los vértices alternados eliminados.

Esta construcción se denomina tetraedro romo en su forma icosaédrica regular, generada por las mismas operaciones realizadas a partir del vector ( ϕ , 1, 0), donde ϕ es la proporción áurea . ^[3]

En el icosaedro de Jessen, a veces llamado icosaedro ortogonal de Jessen , las 12 caras isósceles están dispuestas de manera diferente para que la figura no sea convexa y tenga ángulos diedros rectos .

Es una tijera congruente con un cubo, lo que significa que se puede cortar en pedazos poliédricos más pequeños que se pueden reorganizar para formar un cubo sólido.

Un icosaedro regular es topológicamente idéntico a un cuboctaedro con sus 6 caras cuadradas bisecadas en diagonales con simetría piritoédrica. Los icosaedros con simetría piritoédrica constituyen una familia infinita de poliedros que incluyen el cuboctaedro, el icosaedro regular, el icosaedro de Jessen y el octaedro de doble recubrimiento . Existen transformaciones cinemáticas cíclicas entre los miembros de esta familia.

El icosaedro rómbico es un zonohedro formado por 20 rombos congruentes. Se puede derivar del triacontaedro rómbico eliminando 10 caras intermedias. Aunque todas las caras son congruentes, el icosaedro rómbico no es transitivo en cuanto a caras .

Los icosaedros comunes con simetrías piramidales y prismáticas incluyen:

• Pirámide de 19 lados (más 1 base = 20).
• Prisma de 18 lados (más 2 extremos = 20).
• Antiprisma de 9 lados (2 conjuntos de 9 lados + 2 extremos = 20).
• Bipirámide de 10 lados (2 conjuntos de 10 lados = 20).
• Trapezoedro de 10 lados (2 conjuntos de 10 lados = 20).

Varios sólidos de Johnson son icosaedros: ^[5]

J22	J35	J36	J59	J60	J92
Cúpula triangular giroelongada	Ortobicúpula triangular alargada	Girobicúpula triangular alargada	Dodecaedro parabiaumentado	Dodecaedro metabiaumentado	Hebesfenorrotunda triangular
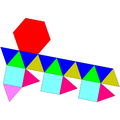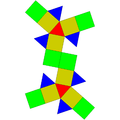16 triángulos 3 cuadrados   1 hexágono	8 triángulos 12 cuadrados	8 triángulos 12 cuadrados	10 triángulos   10 pentágonos	10 triángulos   10 pentágonos	13 triángulos 3 cuadrados 3 pentágonos 1 hexágono

• Icosaedro truncado
• 600 celdas
• Icosoku

Wikimedia Commons tiene medios relacionados con el icosaedro .