Horizonte de eventos

Relatividad general
${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={\kappa }T_{\mu \nu }}$
Introducción Historia Cronología Pruebas Formulación matemática
Conceptos fundamentales Principio de equivalencia Relatividad especial Línea mundial Variedad pseudo-riemanniana
Fenómenos Problema de Kepler Efecto de lente gravitacional Desplazamiento al rojo gravitacional Dilatación del tiempo gravitacional Ondas gravitacionales Arrastre de fotogramas Efecto geodésico Horizonte de eventos Singularidad Agujero negro Espacio-tiempo Diagramas del espacio-tiempo El espacio-tiempo de Minkowski Puente Einstein-Rosen
Ecuaciones Formalismos Ecuaciones Gravedad linealizada Ecuaciones de campo de Einstein Friedman- Geodésicas Mathisson–Papapetrou–Dixon Hamilton-Jacobi-Einstein Formalismos ADM BSSN Post-Newtoniano Teoría avanzada Teoría de Kaluza-Klein Gravedad cuántica
Soluciones Niño Negro ( interior ) Reissner–Nordström Ondas de Einstein-Rosen Agujero de gusano Gödel Kerr Kerr–Newman Kerr–Newman–de Sitter Kasner Lemaître–Tolman Taub–NUT Milne Robertson-Walker Oppenheimer-Snyder onda pp polvo de van Stockum Weyl-Lewis-Papapetrou Hartle–Thorne
Científicos Einstein Lorentz Hilbert Poincaré Niño negro De Sitter Reissner Nordström Weyl Eddington Friedman- Milne Zwicky Lemaître Oppenheimer Gödel Rodador Robertson Bardeen Caminante Kerr Chandrasekhar Síndrome de Ehlers Penrose Halcones Raychaudhuri Taylor Hulse de Stockum Tabaquismo Hombre nuevo Yaú Espina otros
Portal de física  Categoría
en a mi

En astrofísica , un horizonte de sucesos es un límite más allá del cual los sucesos no pueden afectar a un observador. Wolfgang Rindler acuñó el término en la década de 1950. ^[1]

En 1784, John Michell propuso que la gravedad puede ser lo suficientemente fuerte en las proximidades de objetos masivos y compactos como para que ni siquiera la luz pueda escapar. ^[2] En ese momento, la teoría de la gravitación de Newton y la llamada teoría corpuscular de la luz eran dominantes. En estas teorías, si la velocidad de escape de la influencia gravitatoria de un objeto masivo excede la velocidad de la luz , entonces la luz que se origina en su interior o desde él puede escapar temporalmente, pero regresará. En 1958, David Finkelstein utilizó la relatividad general para introducir una definición más estricta de un horizonte de sucesos local de agujero negro como un límite más allá del cual los eventos de cualquier tipo no pueden afectar a un observador externo, lo que conduce a paradojas de información y de cortafuegos , lo que alienta el reexamen del concepto de horizontes de sucesos locales y la noción de agujeros negros. Posteriormente se desarrollaron varias teorías, algunas con y otras sin horizontes de sucesos. Uno de los principales desarrolladores de teorías para describir los agujeros negros, Stephen Hawking , sugirió que se debería utilizar un horizonte aparente en lugar de un horizonte de sucesos, diciendo: "El colapso gravitacional produce horizontes aparentes pero no horizontes de sucesos". Finalmente concluyó que "la ausencia de horizontes de eventos significa que no hay agujeros negros, en el sentido de regímenes de los cuales la luz no puede escapar al infinito ". ^{[3] [4]}

Cualquier objeto que se acerca al horizonte desde el lado del observador parece disminuir su velocidad y nunca llegar a cruzar el horizonte. ^[5] Debido al corrimiento al rojo gravitacional , su imagen se enrojece con el tiempo a medida que el objeto se acerca al horizonte. ^[6]

En un universo en expansión, la velocidad de expansión alcanza —e incluso supera— la velocidad de la luz, lo que impide que las señales viajen a algunas regiones. Un horizonte de sucesos cósmico es un verdadero horizonte de sucesos porque afecta a todo tipo de señales, incluidas las ondas gravitacionales , que viajan a la velocidad de la luz.

Los tipos de horizontes más específicos incluyen los horizontes absoluto y aparente, relacionados pero distintos, que se encuentran alrededor de un agujero negro. Otros tipos distintos incluyen:

• Los horizontes de Cauchy y Killing .
• Las esferas y ergosferas de fotones de la solución de Kerr .
• Partículas y horizontes cosmológicos relevantes para la cosmología .
• Horizontes aislados y dinámicos , que son importantes en la investigación actual de agujeros negros.

En cosmología , el horizonte de sucesos del universo observable es la mayor distancia de comorbilidad desde la que la luz emitida ahora puede llegar al observador en el futuro. Esto difiere del concepto de horizonte de partículas , que representa la mayor distancia de comorbilidad desde la que la luz emitida en el pasado podría llegar al observador en un momento dado. Para los sucesos que ocurren más allá de esa distancia, la luz no ha tenido tiempo suficiente para llegar a nuestra ubicación, incluso si se emitió en el momento en que comenzó el universo. La evolución del horizonte de partículas con el tiempo depende de la naturaleza de la expansión del universo . Si la expansión tiene ciertas características, partes del universo nunca serán observables, sin importar cuánto tiempo espere el observador a que llegue la luz de esas regiones. El límite más allá del cual los eventos nunca pueden observarse es un horizonte de sucesos, y representa la extensión máxima del horizonte de partículas.

El criterio para determinar si existe un horizonte de partículas para el universo es el siguiente. Defina una distancia de comovimiento d _p como

${\displaystyle d_{p}=\int _{0}^{t_{0}}{\frac {c}{a(t)}}\,dt.}$

En esta ecuación, a es el factor de escala , c es la velocidad de la luz y t ₀ es la edad del Universo. Si d _p → ∞ (es decir, apunta arbitrariamente tan lejos como se pueda observar), entonces no existe ningún horizonte de sucesos. Si d _p ≠ ∞ , existe un horizonte.

Ejemplos de modelos cosmológicos sin horizonte de sucesos son los universos dominados por la materia o por la radiación . Un ejemplo de un modelo cosmológico con horizonte de sucesos es un universo dominado por la constante cosmológica (un universo de De Sitter ).

En un artículo sobre el modelo cosmológico FLRW se presentó un cálculo de las velocidades de los horizontes de partículas y eventos cosmológicos , que aproxima el Universo como compuesto de constituyentes que no interactúan, siendo cada uno de ellos un fluido perfecto . ^{[7] [8]}

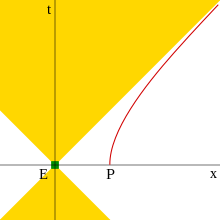
Si una partícula se mueve a una velocidad constante en un universo que no se expande y está libre de campos gravitatorios, cualquier evento que ocurra en ese universo eventualmente será observable por la partícula, porque los conos de luz delanteros de estos eventos intersectan la línea del universo de la partícula . Por otro lado, si la partícula se está acelerando, en algunas situaciones los conos de luz de algunos eventos nunca intersectan la línea del universo de la partícula. Bajo estas condiciones, existe un horizonte aparente en el marco de referencia de la partícula (que se acelera), que representa un límite más allá del cual los eventos son inobservables.

Por ejemplo, esto ocurre con una partícula uniformemente acelerada. En la figura de la derecha se muestra un diagrama espacio-temporal de esta situación. A medida que la partícula acelera, se aproxima, pero nunca alcanza, la velocidad de la luz con respecto a su sistema de referencia original. En el diagrama espacio-temporal, su trayectoria es una hipérbola , que se aproxima asintóticamente a una línea de 45 grados (la trayectoria de un rayo de luz). Un evento cuyo borde del cono de luz sea esta asíntota o esté más alejado que esta asíntota nunca puede ser observado por la partícula en aceleración. En el sistema de referencia de la partícula, hay un límite detrás de ella del cual no pueden escapar señales (un horizonte aparente). La distancia a este límite está dada por , donde a es la aceleración propia constante de la partícula.${\displaystyle c^{2}/a}$

Si bien pueden ocurrir aproximaciones de este tipo de situación en el mundo real ^{[ cita requerida ]} (en aceleradores de partículas , por ejemplo), nunca existe un verdadero horizonte de eventos, ya que esto requiere que la partícula se acelere indefinidamente (lo que requiere cantidades arbitrariamente grandes de energía y un aparato arbitrariamente grande).

En el caso de un horizonte percibido por un observador que acelera uniformemente en el espacio vacío, el horizonte parece permanecer a una distancia fija del observador sin importar cómo se muevan sus alrededores. Variar la aceleración del observador puede hacer que el horizonte parezca moverse con el tiempo o puede impedir que exista un horizonte de sucesos, según la función de aceleración elegida. El observador nunca toca el horizonte y nunca pasa por un lugar en el que parecía estar.

En el caso de un horizonte percibido por un ocupante de un universo de Sitter , el horizonte siempre parece estar a una distancia fija para un observador que no acelera . Nunca entra en contacto con él, ni siquiera un observador que acelera.

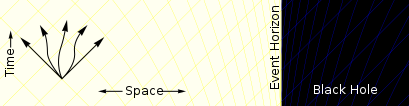Lejos del agujero negro , una partícula puede moverse en cualquier dirección. La única limitación es la velocidad de la luz.

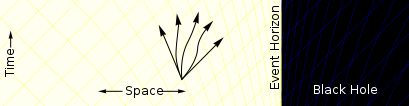A medida que se acerca el agujero negro, el espacio-tiempo comienza a deformarse. En algunos sistemas de coordenadas convenientes, hay más caminos que se dirigen hacia el agujero negro que caminos que se alejan de él. [Nota 1]

Dentro del horizonte de sucesos, todas las trayectorias temporales futuras acercan la partícula al centro del agujero negro. La partícula ya no puede escapar, sin importar la dirección en la que viaje.

Uno de los ejemplos más conocidos de un horizonte de sucesos se deriva de la descripción que hace la relatividad general de un agujero negro, un objeto celeste tan denso que ninguna materia o radiación cercana puede escapar de su campo gravitatorio . A menudo, esto se describe como el límite dentro del cual la velocidad de escape del agujero negro es mayor que la velocidad de la luz . Sin embargo, una descripción más detallada es que dentro de este horizonte, todos los caminos similares a la luz (caminos que la luz podría tomar) (y, por lo tanto, todos los caminos en los conos de luz delanteros de las partículas dentro del horizonte) se deforman para caer más profundamente en el agujero. Una vez que una partícula está dentro del horizonte, moverse hacia el agujero es tan inevitable como moverse hacia adelante en el tiempo, sin importar en qué dirección se esté moviendo la partícula, y puede considerarse equivalente a hacerlo, dependiendo del sistema de coordenadas del espacio-tiempo utilizado. ^{[10] [9] [11] [12]}

La superficie en el radio de Schwarzschild actúa como un horizonte de sucesos en un cuerpo no giratorio que encaja dentro de este radio (aunque un agujero negro giratorio funciona de forma ligeramente diferente). El radio de Schwarzschild de un objeto es proporcional a su masa. Teóricamente, cualquier cantidad de materia se convertirá en un agujero negro si se comprime en un espacio que encaje dentro de su radio de Schwarzschild correspondiente. Para la masa del Sol , este radio es de aproximadamente 3 kilómetros (1,9 millas); para la Tierra , es de unos 9 milímetros (0,35 pulgadas). Sin embargo, en la práctica, ni la Tierra ni el Sol tienen la masa necesaria (y, por lo tanto, la fuerza gravitacional necesaria) para superar la presión de degeneración de electrones y neutrones . La masa mínima requerida para que una estrella colapse más allá de estas presiones es el límite de Tolman-Oppenheimer-Volkoff , que es de aproximadamente tres masas solares.

Según los modelos fundamentales de colapso gravitacional, ^[13] se forma un horizonte de sucesos antes de la singularidad de un agujero negro. Si todas las estrellas de la Vía Láctea se fueran agregando gradualmente hacia el centro galáctico manteniendo las distancias proporcionales entre sí, todas caerían dentro de su radio de Schwarzschild conjunto mucho antes de verse obligadas a colisionar. ^[4] Hasta el colapso en el futuro lejano, los observadores en una galaxia rodeada por un horizonte de sucesos continuarían con sus vidas normalmente.

Los horizontes de sucesos de los agujeros negros son ampliamente malentendidos. Es común, aunque errónea, la idea de que los agujeros negros "aspiran" material en su vecindad, cuando en realidad no son más capaces de buscar material para consumir que cualquier otro atractor gravitacional. Como ocurre con cualquier masa del universo, la materia debe estar dentro de su alcance gravitacional para que exista la posibilidad de captura o consolidación con cualquier otra masa. Igualmente común es la idea de que se puede observar la materia cayendo en un agujero negro. Esto no es posible. Los astrónomos sólo pueden detectar discos de acreción alrededor de los agujeros negros, donde el material se mueve a tal velocidad que la fricción crea una radiación de alta energía que se puede detectar (de manera similar, parte de la materia de estos discos de acreción es expulsada a lo largo del eje de giro del agujero negro, creando chorros visibles cuando estas corrientes interactúan con materia como el gas interestelar o cuando se dirigen directamente a la Tierra). Además, un observador distante nunca verá realmente algo llegar al horizonte. En cambio, a medida que se acerca al agujero, el objeto parecerá moverse cada vez más lentamente, mientras que cualquier luz que emita estará cada vez más desplazada hacia el rojo.

Topológicamente, el horizonte de sucesos se define a partir de la estructura causal como el cono nulo pasado de la infinitud temporal conforme futura. Un horizonte de sucesos de agujero negro es de naturaleza teleológica , lo que significa que está determinado por causas futuras. ^{[14] [15] [16]} Más precisamente, uno necesitaría conocer toda la historia del universo y todo el camino hasta el futuro infinito para determinar la presencia de un horizonte de sucesos, lo que no es posible para los observadores cuasilocales (ni siquiera en principio). ^{[17] [18]} En otras palabras, no hay ningún experimento y/o medición que pueda realizarse dentro de una región de tamaño finito del espacio-tiempo y dentro de un intervalo de tiempo finito que responda a la pregunta de si existe o no un horizonte de sucesos. Debido a la naturaleza puramente teórica del horizonte de sucesos, el objeto que viaja no necesariamente experimenta efectos extraños y, de hecho, pasa a través del límite calculado en una cantidad finita de su tiempo propio . ^[19]

Un error de concepto sobre los horizontes de sucesos, especialmente los de los agujeros negros , es que representan una superficie inmutable que destruye los objetos que se acercan a ellos. En la práctica, todos los horizontes de sucesos parecen estar a cierta distancia de cualquier observador, y los objetos enviados hacia un horizonte de sucesos nunca parecen cruzarlo desde el punto de vista del observador que los envía (ya que el cono de luz del suceso que cruza el horizonte nunca intersecta la línea del mundo del observador ). Intentar hacer que un objeto cercano al horizonte permanezca estacionario con respecto a un observador requiere aplicar una fuerza cuya magnitud aumenta ilimitadamente (hasta volverse infinita) a medida que se acerca.

En el caso del horizonte alrededor de un agujero negro, los observadores estacionarios con respecto a un objeto distante estarán todos de acuerdo en dónde está el horizonte. Si bien esto parece permitir que un observador bajado hacia el agujero en una cuerda (o varilla) entre en contacto con el horizonte, en la práctica esto no se puede hacer. La distancia adecuada al horizonte es finita, ^[20] por lo que la longitud de cuerda necesaria también sería finita, pero si la cuerda se bajara lentamente (de modo que cada punto de la cuerda estuviera aproximadamente en reposo en coordenadas de Schwarzschild ), la aceleración adecuada ( fuerza G ) experimentada por los puntos de la cuerda cada vez más cercanos al horizonte se acercaría al infinito, por lo que la cuerda se rompería. Si la cuerda se baja rápidamente (quizás incluso en caída libre ), entonces, de hecho, el observador en la parte inferior de la cuerda puede tocar e incluso cruzar el horizonte de sucesos. Pero una vez que esto sucede, es imposible sacar la parte inferior de la cuerda del horizonte de sucesos, ya que si se tira de la cuerda con fuerza, las fuerzas a lo largo de la cuerda aumentan sin límite a medida que se acercan al horizonte de sucesos y en algún momento la cuerda debe romperse. Además, la ruptura no debe ocurrir en el horizonte de sucesos, sino en un punto donde el segundo observador pueda observarla.

Suponiendo que el posible horizonte aparente está muy dentro del horizonte de sucesos, o que no hay ninguno, los observadores que cruzan el horizonte de sucesos de un agujero negro en realidad no verían ni sentirían que sucediera nada especial en ese momento. En términos de apariencia visual, los observadores que caen en el agujero perciben el horizonte aparente final como un área negra impermeable que encierra la singularidad. ^[21] Otros objetos que hubieran entrado en el área del horizonte a lo largo del mismo camino radial pero en un momento anterior aparecerían debajo del observador siempre que no ingresen dentro del horizonte aparente, y podrían intercambiar mensajes. Las fuerzas de marea crecientes también son efectos localmente perceptibles, en función de la masa del agujero negro. En los agujeros negros estelares realistas , la espaguetificación ocurre temprano: las fuerzas de marea desgarran los materiales mucho antes del horizonte de sucesos. Sin embargo, en los agujeros negros supermasivos , que se encuentran en los centros de las galaxias, la espaguetificación ocurre dentro del horizonte de sucesos. Un astronauta humano sobreviviría a la caída a través de un horizonte de sucesos solo en un agujero negro con una masa de aproximadamente 10.000 masas solares o más. ^[22]

Un horizonte de eventos cósmico se acepta comúnmente como un horizonte de eventos real, mientras que la descripción de un horizonte de eventos de agujero negro local dada por la relatividad general se considera incompleta y controvertida. ^{[3] [4]} Cuando las condiciones bajo las cuales ocurren los horizontes de eventos locales se modelan utilizando una imagen más completa de cómo funciona el Universo, que incluye tanto la relatividad como la mecánica cuántica , se espera que los horizontes de eventos locales tengan propiedades que sean diferentes de las predichas utilizando solo la relatividad general.

En la actualidad, el mecanismo de radiación de Hawking supone que el principal impacto de los efectos cuánticos es que los horizontes de sucesos posean una temperatura y, por lo tanto, emitan radiación. En el caso de los agujeros negros, esto se manifiesta como radiación de Hawking , y la cuestión más amplia de cómo el agujero negro posee una temperatura forma parte del tema de la termodinámica de los agujeros negros . En el caso de las partículas en aceleración, esto se manifiesta como el efecto Unruh , que hace que el espacio alrededor de la partícula parezca estar lleno de materia y radiación.

Según la controvertida hipótesis del cortafuegos del agujero negro , la materia que cayera en un agujero negro sería quemada por un "cortafuegos" de alta energía en el horizonte de sucesos.

Una alternativa la proporciona el principio de complementariedad , según el cual, en el mapa del observador lejano, la materia que cae se termaliza en el horizonte y se reemite como radiación de Hawking, mientras que en el mapa de un observador que cae la materia continúa sin perturbaciones a través de la región interior y se destruye en la singularidad. Esta hipótesis no viola el teorema de no clonación ya que hay una única copia de la información según cualquier observador dado. La complementariedad de los agujeros negros está sugerida en realidad por las leyes de escala de las cuerdas que se acercan al horizonte de sucesos, lo que sugiere que en el mapa de Schwarzschild se estiran para cubrir el horizonte y se termalizan en una membrana de espesor de longitud de Planck .

Se espera que una descripción completa de los horizontes de eventos locales generados por la gravedad requiera, como mínimo, una teoría de la gravedad cuántica . Una de esas teorías candidatas es la teoría M. Otra teoría candidata de ese tipo es la gravedad cuántica de bucles .

• Fuerza de Abraham-Lorentz
• Métrica acústica
• Más allá de los agujeros negros
• Electrón de agujero negro
• Nave espacial del agujero negro
• Hipótesis de la censura cósmica
• Horizonte dinámico
• Telescopio del Horizonte de Sucesos
• Radiación de Hawking
• Kugelblitz (astrofísica)
• Microagujero negro
• Coordenadas de Rindler

• Misner, Charles W .; Thorne, Kip S .; Wheeler, John Archibald (1973). Gravitación (27.ª edición). Nueva York, NY: Freeman. ISBN 978-0-7167-0344-0.
• Hawking, Stephen W. (2001). El universo en pocas palabras . Nueva York: Bantam. ISBN 978-0-553-80202-3.
• Thorne, Kip S. (1994). Agujeros negros y distorsiones temporales: el escandaloso legado de Einstein . The Commonwealth Fund Book Program. Nueva York/Londres: Norton. ISBN 978-0-393-31276-8.
• Ashtekar, Abhay; Krishnan, Badri (2004). "Horizontes aislados y dinámicos y sus aplicaciones". Living Reviews in Relativity . 7 (1): 10. arXiv : gr-qc/0407042 . Bibcode :2004LRR.....7...10A. doi : 10.12942/lrr-2004-10 . ISSN  2367-3613. PMC  5253930 . PMID  28163644.