Horizonte

El horizonte es la curva aparente que separa la superficie de un cuerpo celeste de su cielo cuando se observa desde la perspectiva de un observador que se encuentra sobre la superficie del cuerpo en cuestión o cerca de ella. Esta curva divide todas las direcciones de observación en función de si intersecta o no la superficie del cuerpo en cuestión.

El horizonte verdadero es una línea teórica, que solo se puede observar con cierto grado de precisión cuando se encuentra a lo largo de una superficie relativamente lisa, como la de los océanos de la Tierra . En muchos lugares, esta línea está oscurecida por el terreno , y en la Tierra también puede estar oscurecida por formas de vida como árboles y/o construcciones humanas como edificios. La intersección resultante de tales obstrucciones con el cielo se llama horizonte visible . En la Tierra, cuando se mira un mar desde una orilla, la parte del mar más cercana al horizonte se llama horizonte visible . ^[1]

El horizonte verdadero rodea al observador y normalmente se supone que es un círculo, dibujado en la superficie de un modelo perfectamente esférico del cuerpo celeste relevante, es decir, un pequeño círculo de la esfera osculadora local . Con respecto a la Tierra, el centro del horizonte verdadero está por debajo del observador y por debajo del nivel del mar . Su radio o distancia horizontal desde el observador varía ligeramente de un día para otro debido a la refracción atmosférica, que se ve muy afectada por las condiciones meteorológicas . Además, cuanto más altos estén los ojos del observador del nivel del mar, más lejos estará el horizonte del observador. Por ejemplo, en condiciones atmosféricas estándar , para un observador con el nivel de los ojos por encima del nivel del mar a 1,8 metros (6 pies), el horizonte está a una distancia de aproximadamente 4,8 kilómetros (3 millas). ^[2] Cuando se observa desde puntos de vista muy altos, como una estación espacial , el horizonte está mucho más lejos y abarca un área mucho más grande de la superficie de la Tierra. En este caso, el horizonte ya no sería un círculo perfecto, ni siquiera una curva plana como una elipse, especialmente cuando el observador está por encima del ecuador, ya que la superficie de la Tierra puede modelarse mejor como un elipsoide achatado que como una esfera.

La palabra horizonte deriva del griego ὁρίζων κύκλος ( horízōn kýklos ) 'círculo separador', ^[3] donde ὁρίζων proviene del verbo ὁρίζω ( horízō ) 'dividir, separar', ^[4] que a su vez deriva de ὅρος ( hóros ) 'límite, hito'. ^[5]

Históricamente, la distancia al horizonte visible ha sido vital para la supervivencia y el éxito de la navegación, especialmente en el mar, porque determinaba el alcance máximo de visión de un observador y, por lo tanto, de comunicación , con todas las consecuencias obvias para la seguridad y la transmisión de información que este alcance implicaba. Esta importancia disminuyó con el desarrollo de la radio y el telégrafo , pero incluso hoy, cuando se vuela una aeronave bajo reglas de vuelo visual , se utiliza una técnica llamada vuelo de actitud para controlar la aeronave, donde el piloto usa la relación visual entre el morro de la aeronave y el horizonte para controlar la aeronave. Los pilotos también pueden conservar su orientación espacial haciendo referencia al horizonte.

En muchos contextos, especialmente en el dibujo en perspectiva , se ignora la curvatura de la Tierra y se considera que el horizonte es la línea teórica a la que convergen los puntos de cualquier plano horizontal (cuando se proyectan sobre el plano de la imagen) a medida que aumenta su distancia del observador. Para los observadores que se encuentran cerca del nivel del mar, la diferencia entre este horizonte geométrico (que supone un plano de tierra infinito y perfectamente plano) y el horizonte verdadero (que supone una superficie terrestre esférica ) es imperceptible a simple vista. Sin embargo, para alguien que se encuentre en una colina de 1000 m (3300 pies) mirando hacia el mar, el horizonte verdadero estará aproximadamente un grado por debajo de una línea horizontal.

En astronomía, el horizonte es el plano horizontal que se ve a través de los ojos del observador. Es el plano fundamental del sistema de coordenadas horizontales , el lugar geométrico de los puntos que tienen una altitud de cero grados. Si bien es similar en algunos aspectos al horizonte geométrico, en este contexto se puede considerar que un horizonte es un plano en el espacio, en lugar de una línea en un plano de imagen.

Ignorando el efecto de la refracción atmosférica, la distancia al horizonte verdadero desde un observador cercano a la superficie de la Tierra es de aproximadamente ^[2]

${\displaystyle d\approx {\sqrt {2\,h\,R}}\,,}$

donde h es la altura sobre el nivel del mar y R es el radio de la Tierra .

La expresión se puede simplificar así:

${\displaystyle d\approx k{\sqrt {h}}\,,}$

donde la constante es igual a k =3,57 km/ ^m½ =1,22 mi/ft ^½ . En esta ecuación, se supone que la superficie de la Tierra es perfectamente esférica, con R igual a aproximadamente 6.371 kilómetros (3.959 mi).

Suponiendo que no hay refracción atmosférica y una Tierra esférica con un radio R=6.371 kilómetros (3.959 millas):

• Para un observador situado en el suelo con h = 1,70 metros (5 pies 7 pulgadas), el horizonte está a una distancia de 4,7 kilómetros (2,9 millas).
• Para un observador situado en el suelo con h = 2 metros (6 pies 7 pulgadas), el horizonte está a una distancia de 5 kilómetros (3,1 millas).
• Para un observador situado en una colina o torre a 30 metros (98 pies) sobre el nivel del mar, el horizonte está a una distancia de 19,6 kilómetros (12,2 millas).
• Para un observador situado en una colina o torre a 100 metros (330 pies) sobre el nivel del mar, el horizonte está a una distancia de 36 kilómetros (22 millas).
• Para un observador situado en el tejado del Burj Khalifa , a 828 metros (2.717 pies) del suelo y a unos 834 metros (2.736 pies) sobre el nivel del mar, el horizonte está a una distancia de 103 kilómetros (64 millas).
• Para un observador en la cima del Monte Everest (8.848 metros (29.029 pies) de altitud), el horizonte está a una distancia de 336 kilómetros (209 millas).
• Para un observador a bordo de un avión comercial de pasajeros que vuela a una altitud típica de 35.000 pies (11.000 m), el horizonte está a una distancia de 369 kilómetros (229 millas).
• Para un piloto de U-2 , mientras vuela a su techo de servicio de 21.000 metros (69.000 pies), el horizonte está a una distancia de 517 kilómetros (321 millas).

En los planetas terrestres y otros cuerpos celestes sólidos con efectos atmosféricos insignificantes, la distancia al horizonte para un "observador estándar" varía según la raíz cuadrada del radio del planeta. Así, el horizonte en Mercurio está a un 62% de la distancia al observador que en la Tierra, en Marte la distancia es del 73%, en la Luna es del 52%, en Mimas es del 18%, y así sucesivamente.

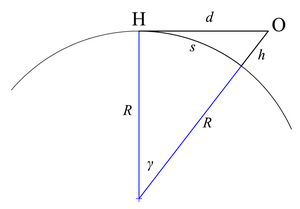
Si se supone que la Tierra es una esfera sin rasgos distintivos (en lugar de un esferoide achatado ) sin refracción atmosférica, entonces la distancia al horizonte se puede calcular fácilmente. ^[6]

El teorema de la tangente-secante establece que

${\displaystyle \mathrm {OC} ^{2}=\mathrm {OA} \times \mathrm {OB} \,.}$

Realice las siguientes sustituciones:

• d = OC = distancia al horizonte
• D = AB = diámetro de la Tierra
• h = OB = altura del observador sobre el nivel del mar
• D+h = OA = diámetro de la Tierra más la altura del observador sobre el nivel del mar,

donde d, D y h se miden en las mismas unidades. La fórmula ahora se convierte en

${\displaystyle d^{2}=h(D+h)\,\!}$

o

${\displaystyle d={\sqrt {h(D+h)}}={\sqrt {h(2R+h)}}\,,}$

donde R es el radio de la Tierra.

La misma ecuación también se puede derivar utilizando el teorema de Pitágoras . En el horizonte, la línea de visión es tangente a la Tierra y también es perpendicular al radio de la Tierra. Esto establece un triángulo rectángulo, con la suma del radio y la altura como hipotenusa.

• d = distancia al horizonte
• h = altura del observador sobre el nivel del mar
• R = radio de la Tierra

Haciendo referencia a la segunda figura de la derecha llegamos a lo siguiente:

${\displaystyle (R+h)^{2}=R^{2}+d^{2}\,\!}$

${\displaystyle R^{2}+2Rh+h^{2}=R^{2}+d^{2}\,\!}$

${\displaystyle d={\sqrt {h(2R+h)}}\,.}$

La fórmula exacta anterior se puede ampliar como:

${\displaystyle d={\sqrt {2Rh+h^{2}}}\,,}$

donde R es el radio de la Tierra ( R y h deben estar en las mismas unidades). Por ejemplo, si un satélite está a una altura de 2000 km, la distancia al horizonte es de 5430 kilómetros (3370 mi); si se descuida el segundo término entre paréntesis, se obtendría una distancia de 5048 kilómetros (3137 mi), un error del 7%.

Si el observador está cerca de la superficie de la Tierra, entonces es válido ignorar h en el término (2 R + h ) , y la fórmula se convierte en:

${\displaystyle d={\sqrt {2Rh}}\,.}$

Usando kilómetros para d y R , y metros para h , y tomando el radio de la Tierra como 6371 km, la distancia al horizonte es

${\displaystyle d\approx {\sqrt {2\cdot 6371\cdot {h/1000}}}\approx 3.570{\sqrt {h}}\,}$.

Usando unidades imperiales , con d y R en millas terrestres (como se usan comúnmente en tierra) y h en pies, la distancia al horizonte es

${\displaystyle d\approx {\sqrt {2\cdot 3963\cdot {h/5280}}}\approx {\sqrt {1.5h}}\approx 1.22{\sqrt {h}}}$.

Si d está en millas náuticas y h en pies, el factor constante es aproximadamente 1,06, que es lo suficientemente cercano a 1 como para que a menudo se ignore, lo que da:

${\displaystyle d\approx {\sqrt {h}}}$

Estas fórmulas se pueden utilizar cuando h es mucho menor que el radio de la Tierra (6371 km o 3959 mi), incluidas todas las vistas desde cimas de montañas, aviones o globos aerostáticos de gran altitud. Con las constantes dadas, tanto las fórmulas métricas como las imperiales tienen una precisión de 1 % (consulte la siguiente sección para obtener mayor precisión). Si h es significativa con respecto a R , como ocurre con la mayoría de los satélites, entonces la aproximación ya no es válida y se requiere la fórmula exacta.

Otra relación involucra la distancia del círculo máximo s a lo largo del arco sobre la superficie curva de la Tierra hasta el horizonte; esto es más directamente comparable a la distancia geográfica en un mapa.

Se puede formular en términos de γ en radianes ,

${\displaystyle s=R\gamma \,;}$

entonces

${\displaystyle \cos \gamma =\cos {\frac {s}{R}}={\frac {R}{R+h}}\,.}$

Resolviendo para s obtenemos

${\displaystyle s=R\cos ^{-1}{\frac {R}{R+h}}\,.}$

La distancia s también se puede expresar en términos de la distancia de línea de visión d ; de la segunda figura a la derecha,

${\displaystyle \tan \gamma ={\frac {d}{R}}\,;}$

Sustituyendo γ y reordenando obtenemos

${\displaystyle s=R\tan ^{-1}{\frac {d}{R}}\,.}$

Las distancias d y s son casi las mismas cuando la altura del objeto es insignificante en comparación con el radio (es decir, h  ≪  R ).

Cuando el observador está elevado, el ángulo cenital del horizonte puede ser mayor de 90°. El ángulo cenital máximo visible se produce cuando el rayo es tangente a la superficie de la Tierra; desde el triángulo OCG en la figura de la derecha,

${\displaystyle \cos \gamma ={\frac {R}{R+h}}}$

donde es la altura del observador sobre la superficie y es la inclinación angular del horizonte. Está relacionada con el ángulo cenital del horizonte por:${\estilo de visualización h}$${\estilo de visualización \gamma}$${\estilo de visualización z}$

${\displaystyle z=\gamma +90{}^{\circ }}$

Para una altura no negativa , el ángulo siempre es ≥ 90°.${\estilo de visualización h}$${\estilo de visualización z}$

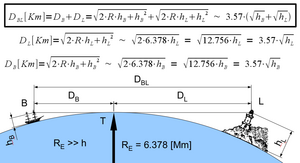
Para calcular la distancia máxima D _BL a la que un observador B puede ver la parte superior de un objeto L sobre el horizonte, simplemente sume las distancias al horizonte desde cada uno de los dos puntos:

DBL = DB + DL_​​​

Por ejemplo, para un observador B con una altura de h _B = 1,70 m de pie en el suelo, el horizonte está a D _B = 4,65 km de distancia. Para una torre con una altura de h _L = 100 m, la distancia al horizonte es D _L = 35,7 km. Por lo tanto, un observador en una playa puede ver la parte superior de la torre siempre que no esté a más de D _BL = 40,35 km de distancia. Por el contrario, si un observador en un barco ( h _B = 1,7  m) puede ver solo las copas de los árboles en una orilla cercana ( h _L = 10  m), los árboles probablemente estén a unos D _BL = 16 km de distancia.

Con referencia a la figura de la derecha y utilizando la aproximación anterior, la parte superior del faro será visible para un vigía en un nido de cuervo en la parte superior de un mástil del barco si

${\displaystyle D_{\mathrm {BL} }<3.57\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,,}$

donde D _BL está en kilómetros y h _B y h _L están en metros.

Como otro ejemplo, supongamos que un observador, cuyos ojos están a dos metros por encima del nivel del suelo, utiliza unos binoculares para mirar a lo lejos un edificio que sabe que consta de treinta pisos , cada uno de 3,5 metros de altura. Cuenta los pisos que puede ver y descubre que sólo hay diez. Por tanto, veinte pisos o 70 metros del edificio quedan ocultos para él por la curvatura de la Tierra. A partir de esto, puede calcular la distancia a la que se encuentra hasta el edificio:

${\displaystyle D\aprox 3,57({\sqrt {2}}+{\sqrt {70}})}$

lo que equivale a unos 35 kilómetros.

De manera similar, es posible calcular qué parte de un objeto distante es visible por encima del horizonte. Supongamos que el ojo de un observador está a 10 metros sobre el nivel del mar y está observando un barco que se encuentra a 20 km de distancia. Su horizonte es:

${\displaystyle 3.57{\sqrt {10}}}$

kilómetros de él, lo que equivale a unos 11,3 kilómetros de distancia. El barco se encuentra a 8,7 kilómetros más. La altura de un punto del barco que es apenas visible para el observador viene dada por:

${\displaystyle h\approx \izquierda({\frac {8.7}{3.57}}\derecha)^{2}}$

lo que equivale a casi exactamente seis metros. El observador puede ver entonces la parte del barco que se encuentra a más de seis metros por encima del nivel del agua. La parte del barco que se encuentra por debajo de esta altura queda oculta a él por la curvatura de la Tierra. En esta situación, se dice que el barco está hull-down (casco hundido) .

Debido a la refracción atmosférica, la distancia hasta el horizonte visible es mayor que la distancia basada en un cálculo geométrico simple. Si la superficie del suelo (o del agua) es más fría que el aire que hay sobre ella, se forma una capa de aire frío y denso cerca de la superficie, lo que hace que la luz se refracte hacia abajo a medida que viaja y, por lo tanto, en cierta medida, rodee la curvatura de la Tierra. Lo contrario ocurre si el suelo es más caliente que el aire que hay sobre él, como suele ocurrir en los desiertos, lo que produce espejismos . Como compensación aproximada por la refracción, los topógrafos que miden distancias superiores a 100 metros restan un 14% del error de curvatura calculado y se aseguran de que las líneas de visión estén al menos a 1,5 metros del suelo, para reducir los errores aleatorios creados por la refracción.

Si la Tierra fuera un mundo sin aire como la Luna, los cálculos anteriores serían precisos. Sin embargo, la Tierra tiene una atmósfera de aire , cuya densidad e índice de refracción varían considerablemente dependiendo de la temperatura y la presión. Esto hace que el aire refracte la luz en diferentes grados, lo que afecta la apariencia del horizonte. Por lo general, la densidad del aire justo por encima de la superficie de la Tierra es mayor que su densidad a mayores altitudes. Esto hace que su índice de refracción sea mayor cerca de la superficie que a mayores altitudes, lo que hace que la luz que viaja aproximadamente en horizontal se refracte hacia abajo. ^[7] Esto hace que la distancia real al horizonte sea mayor que la distancia calculada con fórmulas geométricas. Con condiciones atmosféricas estándar, la diferencia es de aproximadamente el 8%. Esto cambia el factor de 3,57, en las fórmulas métricas utilizadas anteriormente, a aproximadamente 3,86. ^[2] Por ejemplo, si un observador está de pie en la orilla del mar, con los ojos a 1,70 m sobre el nivel del mar, de acuerdo con las fórmulas geométricas simples dadas, el horizonte debería estar a 4,7 km de distancia. En realidad, la refracción atmosférica permite al observador ver 300 metros más lejos, alejando el horizonte verdadero 5 km del observador.

Esta corrección puede aplicarse, y a menudo se aplica, como una aproximación bastante buena cuando las condiciones atmosféricas están cerca de las estándar . Cuando las condiciones son inusuales, esta aproximación falla. La refracción se ve fuertemente afectada por los gradientes de temperatura, que pueden variar considerablemente de un día para otro, especialmente sobre el agua. En casos extremos, generalmente en primavera, cuando el aire cálido se superpone al agua fría, la refracción puede permitir que la luz siga la superficie de la Tierra durante cientos de kilómetros. Las condiciones opuestas ocurren, por ejemplo, en los desiertos, donde la superficie es muy caliente, por lo que el aire caliente y de baja densidad está debajo del aire más frío. Esto hace que la luz se refracte hacia arriba, causando efectos de espejismo que hacen que el concepto de horizonte carezca de algún sentido. Por lo tanto, los valores calculados para los efectos de la refracción en condiciones inusuales son solo aproximados. ^[2] Sin embargo, se han realizado intentos para calcularlos con mayor precisión que la simple aproximación descrita anteriormente.

Fuera del rango de longitud de onda visual, la refracción será diferente. Para el radar (por ejemplo, para longitudes de onda de 300 a 3 mm, es decir, frecuencias entre 1 y 100 GHz), el radio de la Tierra se puede multiplicar por 4/3 para obtener un radio efectivo que da un factor de 4,12 en la fórmula métrica, es decir, el horizonte del radar estará un 15 % más allá del horizonte geométrico o un 7 % más allá del visual. El factor 4/3 no es exacto, ya que en el caso visual la refracción depende de las condiciones atmosféricas.

Método de integración—Sweer

Si se conoce el perfil de densidad de la atmósfera, la distancia d al horizonte viene dada por ^[8]

${\displaystyle d={{R}_{\text{E}}}\left(\psi +\delta \right)\,,}$

donde R _E es el radio de la Tierra, ψ es la inclinación del horizonte y δ es la refracción del horizonte. La inclinación se determina de manera bastante simple a partir de

${\displaystyle \cos \psi ={\frac {{R}_{\text{E}}{\mu }_{0}}{\left({{R}_{\text{E}}}+h\right)\mu }}\,,}$

donde h es la altura del observador sobre la Tierra, μ es el índice de refracción del aire a la altura del observador y μ ₀ es el índice de refracción del aire en la superficie de la Tierra.

La refracción debe encontrarse mediante la integración de

${\displaystyle \delta =-\int _{0}^{h}{\tan \phi {\frac {{\text{d}}\mu }{\mu }}}\,,}$

donde es el ángulo entre el rayo y una línea que pasa por el centro de la Tierra. Los ángulos ψ y están relacionados por${\estilo de visualización \phi \,\!}$${\estilo de visualización \phi \,\!}$

${\displaystyle \phi =90{}^{\circ }-\psi \,.}$

Método sencillo: Young

Un enfoque mucho más simple, que produce esencialmente los mismos resultados que la aproximación de primer orden descrita anteriormente, utiliza el modelo geométrico pero utiliza un radio R′ = 7/6 R _E . La distancia al horizonte es entonces ^[2]

${\displaystyle d={\sqrt {2R^{\prime }h}}\,.}$

Tomando el radio de la Tierra como 6371 km, con d en km y h en m,

${\displaystyle d\approx 3,86{\sqrt {h}}\,;}$

con d en mi y h en ft,

${\displaystyle d\approx 1,32{\sqrt {h}}\,.}$

En el caso del radar, normalmente se tiene R′ = 4/3 R _E , lo que resulta (con d en km y h en m) en

${\displaystyle d\approx 4,12{\sqrt {h}}\,;}$

Los resultados del método de Young son bastante similares a los del método de Sweer y son suficientemente precisos para muchos propósitos.

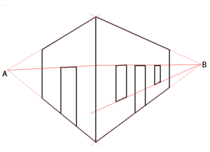
El horizonte es una característica clave del plano de la imagen en la ciencia de la perspectiva gráfica . Suponiendo que el plano de la imagen se encuentra vertical al suelo y que P es la proyección perpendicular del punto de observación O sobre el plano de la imagen, el horizonte se define como la línea horizontal que pasa por P. El punto P es el punto de fuga de las líneas perpendiculares a la imagen. Si S es otro punto en el horizonte, entonces es el punto de fuga de todas las líneas paralelas a OS . Pero Brook Taylor (1719) indicó que el plano del horizonte determinado por O y el horizonte eran como cualquier otro plano :

El término de línea horizontal, por ejemplo, tiende a confinar las nociones de un estudiante al plano del horizonte y a hacerle imaginar que ese plano goza de algunos privilegios particulares que hacen que las figuras que contiene sean más fáciles y más convenientes de describir por medio de esa línea horizontal que las figuras de cualquier otro plano... Pero en este libro no hago ninguna diferencia entre el plano del horizonte y cualquier otro plano... ^{[9] [10]}

La peculiar geometría de la perspectiva, en la que las líneas paralelas convergen en la distancia, estimuló el desarrollo de la geometría proyectiva , que postula un punto en el infinito donde se encuentran las líneas paralelas. En su libro Geometry of an Art (2007), Kirsti Andersen describió la evolución del dibujo en perspectiva y la ciencia hasta 1800, señalando que los puntos de fuga no necesitan estar en el horizonte. En un capítulo titulado "Horizonte", John Stillwell relató cómo la geometría proyectiva ha llevado a la geometría de incidencia , el estudio abstracto moderno de la intersección de líneas. Stillwell también se aventuró en los fundamentos de las matemáticas en una sección titulada "¿Cuáles son las leyes del álgebra?". El "álgebra de puntos", originalmente propuesta por Karl von Staudt para derivar los axiomas de un campo, fue deconstruida en el siglo XX, lo que produjo una amplia variedad de posibilidades matemáticas. Stillwell afirma

Este descubrimiento, de hace 100 años, parece capaz de poner patas arriba las matemáticas, aunque todavía no ha sido totalmente asimilado por la comunidad matemática. No sólo desafía la tendencia de convertir la geometría en álgebra, sino que sugiere que tanto la geometría como el álgebra tienen una base más simple de lo que se creía anteriormente. ^[11]

• Young, Andrew T. "Dip of the Horizon". Sitio web Green Flash (Secciones: Refracción astronómica, Agrupamiento del horizonte) . Departamento de Astronomía de la Universidad Estatal de San Diego . Consultado el 16 de abril de 2011 .