Hexominó

Un hexominó (o 6-ominó ) es un poliominó de orden 6, es decir, un polígono en el plano formado por 6 cuadrados de igual tamaño conectados borde con borde. ^[1] El nombre de este tipo de figura se forma con el prefijo hex(a)-. Cuando las rotaciones y las reflexiones no se consideran formas distintas, hay 35 hexominós libres diferentes . Cuando las reflexiones se consideran distintas, hay 60 hexominós de un solo lado . Cuando las rotaciones también se consideran distintas, hay 216 hexominós fijos . ^{[2] [3]}

La figura de arriba muestra los 35 hexominós libres posibles, coloreados según sus grupos de simetría :

• Los veinte hexominós grises no tienen simetría . Su grupo de simetría consiste únicamente en la función identidad .
• Los seis hexóminos rojos tienen un eje de simetría especular paralelo a las líneas de la cuadrícula. Su grupo de simetría tiene dos elementos, la identidad y una reflexión en una línea paralela a los lados de los cuadrados.
• Los dos hexóminos verdes tienen un eje de simetría especular a 45° de las líneas de la cuadrícula. Su grupo de simetría tiene dos elementos, la identidad y una reflexión diagonal.
• Los cinco hexominós azules tienen simetría puntual, también conocida como simetría rotacional de orden 2. Su grupo de simetría tiene dos elementos, la identidad y la rotación de 180°.
• Los dos hexóminos morados tienen dos ejes de simetría especular, ambos paralelos a las líneas de la cuadrícula (es decir, un eje horizontal y un eje vertical). Su grupo de simetría tiene cuatro elementos. Es el grupo diedro de orden 2, también conocido como el grupo de cuatro de Klein .

Si las reflexiones de un hexominó se consideran distintas, como ocurre con los hexominós unilaterales, entonces la primera y la cuarta categoría mencionadas anteriormente duplicarían su tamaño, lo que daría como resultado 25 hexominós adicionales para un total de 60. Si las rotaciones también se consideran distintas, entonces los hexominós de la primera categoría cuentan ocho veces, los de las siguientes tres categorías cuentan cuatro veces y los de la última categoría cuentan dos veces. Esto da como resultado 20 × 8 + (6 + 2 + 5) × 4 + 2 × 2 = 216 hexominós fijos.

Cada uno de los 35 hexominós satisface el criterio de Conway ; por lo tanto, cada hexominó es capaz de teselar el plano. ^[4]

Aunque un conjunto completo de 35 hexominós tiene un total de 210 cuadrados, no es posible empaquetarlos en un rectángulo . (Tal disposición es posible con los 12 pentominós , que se pueden empaquetar en cualquiera de los rectángulos 3 × 20, 4 × 15, 5 × 12 y 6 × 10). Una forma sencilla de demostrar que tal empaquetamiento de hexominós no es posible es mediante un argumento de paridad . Si los hexominós se colocan en un patrón de tablero de ajedrez , entonces 11 de los hexominós cubrirán un número par de cuadrados negros (ya sea 2 blancos y 4 negros o viceversa) y los otros 24 hexominós cubrirán un número impar de cuadrados negros (3 blancos y 3 negros). En general, un número par de cuadrados negros estarán cubiertos en cualquier disposición. Sin embargo, cualquier rectángulo de 210 cuadrados tendrá 105 cuadrados negros y 105 cuadrados blancos, y por lo tanto no puede ser cubierto por los 35 hexominós.

Sin embargo, existen otras figuras sencillas de 210 casillas que se pueden empaquetar con los hexominós. Por ejemplo, un cuadrado de 15 × 15 con un rectángulo de 3 × 5 eliminado del centro tiene 210 casillas. Con el coloreado en tablero de ajedrez, tiene 106 casillas blancas y 104 casillas negras (o viceversa), por lo que la paridad no impide un empaquetamiento, y un empaquetamiento es de hecho posible. ^[5] También es posible que dos conjuntos de piezas encajen en un rectángulo de tamaño 420, o que el conjunto de 60 hexominós de un solo lado (18 de los cuales cubren un número par de casillas negras) encaje en un rectángulo de tamaño 360. ^[6]

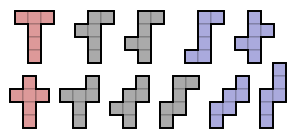
Un desarrollo poliédrico para el cubo es necesariamente un hexominó, con 11 hexominós (mostrados a la derecha) que en realidad son desarrollos. Aparecen a la derecha, nuevamente coloreados de acuerdo con sus grupos de simetría.

Una red poliédrica para el cubo no puede contener el O-tetrominó, ni el I-pentominó, ni el U-pentominó, ni el V-pentominó.

• Página de Jürgen Köller sobre hexóminos, incluyendo simetría, empaquetamiento y otros aspectos
• Página de poliominós del Geometry Junkyard de David Eppstein
• Once animaciones que muestran los patrones del cubo (en francés)
• Teselas de polipolígonos Archivado el 18 de octubre de 2007 en Wayback Machine , Steven Dutch.