Dodecaedro de Disdyakis

Figura geométrica con 48 caras

Dodecaedro de Disdyakis
( modelo giratorio y 3D )
Tipo	Catalán sólido
Notación de Conway	mC
Diagrama de Coxeter
Polígono de cara	triángulo escaleno
Caras	48
Bordes	72
Vértices	26 = 6 + 8 + 12
Configuración de la cara	V4.6.8
Grupo de simetría	Oh , B3 _{, [4,3],}_* 432
Ángulo diedro	155° 4' 56" $\arccos(-{\frac {71+12{\sqrt {2}}}{97}})$
Poliedro dual	cuboctaedro truncado
Propiedades	convexo, transitivo de caras
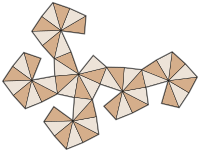neto

En geometría , un dodecaedro disdyakis (también hexoctaedro , ^[1] hexakis octaedro , cubo octakis , hexaedro octakis , dodecaedro kisrómbico ^[2] ) es un sólido catalán con 48 caras y el dual del cuboctaedro truncado de Arquímedes . Como tal, es transitivo en cuanto a las caras, pero con polígonos de caras irregulares. Se parece a un dodecaedro rómbico aumentado . Reemplazar cada cara del dodecaedro rómbico por una pirámide plana crea un poliedro que se parece casi al dodecaedro disdyakis y es topológicamente equivalente a él.

Más formalmente, el dodecaedro disdyakis es el Kleetope del dodecaedro rómbico y la subdivisión baricéntrica del cubo o del octaedro regular . ^[3] La red de la pirámide dodecaédrica rómbica también comparte la misma topología.

Simetría

Tiene simetría octaédrica O _h . Sus aristas colectivas representan los planos de reflexión de la simetría. También se puede ver en la triangulación de las esquinas y aristas medias del cubo regular y del octaedro, y del dodecaedro rómbico.

Dodecaedro de Disdyakis	Icositetraedro deltoidal	Dodecaedro rómbico	Hexaedro	Octaedro

Poliedro esférico

(ver modelo rotatorio )	Proyecciones ortográficas a partir de 2, 3 y 4 ejes

Las aristas de un disdyakis dodecaedro esférico pertenecen a 9 círculos máximos . Tres de ellos forman un octaedro esférico (gris en las imágenes de abajo). Los seis restantes forman tres hosoedros cuadrados (rojo, verde y azul en las imágenes de abajo). Todos ellos corresponden a planos especulares : el primero en simetría diedra [2,2] y el segundo en simetría tetraédrica [3,3].

Proyecciones estereográficas
	Doble pliegue	3 veces	Cuádruple

Coordenadas cartesianas

Sea . Entonces las coordenadas cartesianas para los vértices de un dodecaedro disdyakis centrado en el origen son: $~a={\frac {1}{1+2{\sqrt {2}}}}~{\color {Gris}\aprox 0,261},~~b={\frac {1}{2+3{\sqrt {2}}}}~{\color {Gris}\aprox 0,160},~~c={\frac {1}{3+3{\sqrt {2}}}}~{\color {Gris}\aprox 0,138}$

● permutaciones de (± a , 0, 0) (vértices de un octaedro) ● permutaciones de (± b , ± b , 0) (vértices de un cuboctaedro ) ● (± c , ± c , ± c ) (vértices de un cubo)

Cáscaras convexas
Combinando un octaedro, un cubo y un cuboctaedro para formar el disdyakis dodecaedro. Las envolturas convexas para estos vértices ^[4] escaladas por dan como resultado coordenadas cartesianas de circunradio unitario , que se visualizan en la figura siguiente: ${\estilo de visualización 1/a}$

Dimensiones

Si sus aristas más pequeñas tienen una longitud a , su área superficial y su volumen son

{\begin{aligned}A&={\tfrac {6}{7}}{\sqrt {783+436{\sqrt {2}}}}\,a^{2}\\V&={\tfrac {1}{7}}{\sqrt {3\left(2194+1513{\sqrt {2}}\right)}}a^{3}\end{aligned}}

Las caras son triángulos escalenos. Sus ángulos son , y . $\arccos {\biggl (}{\frac {1}{6}}-{\frac {1}{12}}{\sqrt {2}}{\biggr )}~{\color {Gris}\approx 87.201^{\circ }}$ $\arccos {\biggl (}{\frac {3}{4}}-{\frac {1}{8}}{\sqrt {2}}{\biggr )}~{\color {Gris}\approx 55.024^{\circ }}$ $\arccos {\biggl (}{\frac {1}{12}}+{\frac {1}{2}}{\sqrt {2}}{\biggr )}~{\color {Gris}\approx 37.773^{\circ }}$

Proyecciones ortogonales

El cuboctaedro truncado y su dual, el disdyakisdodecaedro, pueden dibujarse en varias orientaciones proyectivas ortogonales simétricas. Entre un poliedro y su dual, los vértices y las caras están intercambiados en sus posiciones y las aristas son perpendiculares.

Simetría proyectiva	[4]	[3]	[2]	[2]	[2]	[2]	[2] ⁺
Imagen
Imagen dual

Poliedros y teselaciones relacionados


Los poliedros similares al dodecaedro disdyakis son duales del octaedro Bowtie y del cubo , y contienen pares adicionales de caras triangulares. ^[5]

El dodecaedro disdyakis pertenece a una familia de duales de los poliedros uniformes relacionados con el cubo y el octaedro regular.

Poliedros octaédricos uniformes
Simetría : [4,3], (*432)							[4,3] ⁺ (432)	[1 ⁺ ,4,3] = [3,3] (*332)		[3 ⁺ ,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3 ^1,1 }	t{3,4} t{3 ^1,1 }	{3,4} {3 ^1,1 }	_{rr {}4,3} s2 {3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2 {4,3} t _{ 3,3}	s{3,4} s{3 ^1,1 }

		=	=	=				= o	= o	=

De poliedros duales a uniformes
V4 ³	Versión 3.8 ²	V(3.4) ²	Versión 4.6 ²	Versión 3 ⁴	Versión 3.4 ³	V4.6.8	Versión 3 ⁴ .4	V3 ³	Versión 3.6 ²	V3 ⁵

Se trata de un poliedro de una sucesión definida por la configuración de caras V4.6.2 n . Este grupo es especial por tener todos los números pares de aristas por vértice y formar planos biseccionales a través de los poliedros y líneas infinitas en el plano, y continuar en el plano hiperbólico para cualquier n ≥ 7.

Con un número par de caras en cada vértice, estos poliedros y teselas se pueden mostrar alternando dos colores para que todas las caras adyacentes tengan colores diferentes.

Cada cara de estos dominios también corresponde al dominio fundamental de un grupo de simetría con orden 2,3, n espejos en cada vértice de la cara del triángulo.

* n 32 mutación de simetría de teselaciones omnitruncadas: 4.6.2n en a mi
Sím. * n 32 [ n ,3]	Esférico				Euclides.	Hiperb. compacta.		Paraíso.	Hiperbólica no compacta
Sím. * n 32 [ n ,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Cifras
Configuración.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duales
Configuración.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	Versión 4.6.24i	Versión 4.6.18i	Versión 4.6.12i	Versión 4.6.6i

* n 42 mutación de simetría de teselaciones omnitruncadas: 4.8.2n en a mi
Simetría * n 42 [n,4]	Esférico		Euclidiano	Hiperbólica compacta				Paracomp.
Simetría * n 42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Figura omnitruncada	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Duales omnitruncados	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

Véase también

Primera estelación del dodecaedro rómbico
Triacontaedro de Disdyakis
Azulejos de kisrhombille
Gran rombihexacrono : un poliedro dual uniforme con la misma topología de superficie

Referencias

^ "Palabra clave: "formularios" | ClipArt ETC".
^ Conway, Simetrías de las cosas, p.284
^ Langer, Joel C.; Singer, David A. (2010), "Reflexiones sobre la lemniscata de Bernoulli: las cuarenta y ocho caras de una joya matemática", Milan Journal of Mathematics , 78 (2): 643–682, doi :10.1007/s00032-010-0124-5, MR 2781856
^ Koca, Mehmet; Ozdes Koca, Nazife; Koc, Ramazon (2010). "Sólidos Catalanes Derivados de Sistemas de Raíces 3D y Cuaterniones". Journal of Mathematical Physics . 51 (4). arXiv : 0908.3272 . doi :10.1063/1.3356985.
^ Symmetrohedra: Poliedros a partir de la colocación simétrica de polígonos regulares Craig S. Kaplan

Williams, Robert (1979). La base geométrica de la estructura natural: un libro de consulta sobre diseño . Dover Publications, Inc. ISBN 0-486-23729-X.(Sección 3-9)
Las simetrías de las cosas 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 [1] (Capítulo 21, Denominación de los poliedros y teselaciones de Arquímedes y de Catalán, página 285, kisDodecaedro rómbico)

Enlaces externos

Weisstein, Eric W. , "Dodecaedro de Disdyakis" ("Sólido catalán") en MathWorld .
Modelo poliedro interactivo del dodecaedro de Disdyakis (octaedro de Hexakis)

[1] "Palabra clave: "formularios" | ClipArt ETC".

[2] Conway, Simetrías de las cosas, p.284

[3] Langer, Joel C.; Singer, David A. (2010), "Reflexiones sobre la lemniscata de Bernoulli: las cuarenta y ocho caras de una joya matemática", Milan Journal of Mathematics , 78 (2): 643–682, doi :10.1007/s00032-010-0124-5, MR 2781856

[4] Koca, Mehmet; Ozdes Koca, Nazife; Koc, Ramazon (2010). "Sólidos Catalanes Derivados de Sistemas de Raíces 3D y Cuaterniones". Journal of Mathematical Physics . 51 (4). arXiv : 0908.3272 . doi :10.1063/1.3356985.

[5] Symmetrohedra: Poliedros a partir de la colocación simétrica de polígonos regulares Craig S. Kaplan