Familia de cristales hexagonales
| Sistema de cristal | Trigonal | Hexagonal | |
|---|---|---|---|
| Sistema de celosía |  Romboédrico |  Hexagonal | |
| Ejemplo | .jpg/440px-Dolomite_sur_mimétite_(Maroc).jpg) Dolomita (blanca) |  α- Cuarzo |  Berilo |
En cristalografía , la familia de cristales hexagonales es una de las seis familias de cristales , que incluye dos sistemas cristalinos (hexagonal y trigonal ) y dos sistemas reticulares (hexagonal y romboédrico ). Aunque suelen confundirse, el sistema cristalino trigonal y el sistema reticular romboédrico no son equivalentes (véase la sección sobre sistemas cristalinos a continuación). [1] En particular, hay cristales que tienen simetría trigonal pero pertenecen al sistema reticular hexagonal (como el cuarzo α ).
La familia de cristales hexagonales está formada por los 12 grupos puntuales tales que al menos uno de sus grupos espaciales tiene la red hexagonal como red subyacente, y es la unión del sistema cristalino hexagonal y el sistema cristalino trigonal. [2] Hay 52 grupos espaciales asociados a ella, que son exactamente aquellos cuya red de Bravais es hexagonal o romboédrica.
Sistemas de celosía
La familia de cristales hexagonales consta de dos sistemas reticulares : hexagonal y romboédrico. Cada sistema reticular consta de una red de Bravais .

| Celosía de Bravais | Hexagonal | Romboédrico |
|---|---|---|
| Símbolo de Pearson | persona de edad avanzada | hora |
Celda unitaria hexagonal |  | 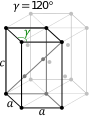 |
Celda unitaria romboédrica |  | 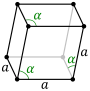 |
En la familia hexagonal, el cristal se describe convencionalmente mediante una celda unitaria de prisma rómbico recto con dos ejes iguales ( a por a ), un ángulo incluido de 120° ( γ ) y una altura ( c , que puede ser diferente de a ) perpendicular a los dos ejes de la base.
La celda unitaria hexagonal para la red de Bravais romboédrica es la celda centrada en R, que consta de dos puntos de red adicionales que ocupan una diagonal del cuerpo de la celda unitaria. Hay dos formas de hacer esto, que pueden considerarse como dos notaciones que representan la misma estructura. En la configuración habitual denominada anverso, los puntos de red adicionales están en las coordenadas ( 2 ⁄ 3 , 1 ⁄ 3 , 1 ⁄ 3 ) y ( 1 ⁄ 3 , 2 ⁄ 3 , 2 ⁄ 3 ), mientras que en la configuración inversa alternativa están en las coordenadas ( 1 ⁄ 3 , 2 ⁄ 3 , 1 ⁄ 3 ) y ( 2 ⁄ 3 , 1 ⁄ 3 , 2 ⁄ 3 ). [3] En cualquier caso, hay 3 puntos reticulares por celda unitaria en total y la red no es primitiva.
Las redes de Bravais en la familia de cristales hexagonales también pueden describirse mediante ejes romboédricos. [4] La celda unitaria es un romboedro (que da el nombre a la red romboédrica). Esta es una celda unitaria con parámetros a = b = c ; α = β = γ ≠ 90°. [5] En la práctica, la descripción hexagonal se utiliza más comúnmente porque es más fácil tratar con un sistema de coordenadas con dos ángulos de 90°. Sin embargo, los ejes romboédricos se muestran a menudo (para la red romboédrica) en los libros de texto porque esta celda revela la simetría de 3 m de la red cristalina.
La celda unitaria romboédrica para la red hexagonal de Bravais es la celda centrada en D [1] , que consta de dos puntos de red adicionales que ocupan una diagonal del cuerpo de la celda unitaria con coordenadas ( 1 ⁄ 3 , 1 ⁄ 3 , 1 ⁄ 3 ) y ( 2 ⁄ 3 , 2 ⁄ 3 , 2 ⁄ 3 ). Sin embargo, dicha descripción rara vez se utiliza.
Sistemas de cristal
| Sistema de cristal | Simetrías requeridas del grupo de puntos | Grupos de puntos | Grupos espaciales | Celosías de Bravais | Sistema de celosía |
|---|---|---|---|---|---|
| Trigonal | 1 eje de rotación triple | 5 | 7 | 1 | Romboédrico |
| 18 | 1 | Hexagonal | |||
| Hexagonal | 1 eje de rotación séxtuple | 7 | 27 |
La familia de cristales hexagonales consta de dos sistemas cristalinos : trigonométrico y hexagonal. Un sistema cristalino es un conjunto de grupos puntuales en el que los propios grupos puntuales y sus correspondientes grupos espaciales están asignados a un sistema reticular (véase la tabla en Sistema cristalino#Clases de cristales ).
El sistema cristalino trigonal consta de 5 grupos puntuales que tienen un único eje de rotación triple, que incluye los grupos espaciales 143 a 167. Estos 5 grupos puntuales tienen 7 grupos espaciales correspondientes (indicados por R) asignados al sistema reticular romboédrico y 18 grupos espaciales correspondientes (indicados por P) asignados al sistema reticular hexagonal. Por lo tanto, el sistema cristalino trigonal es el único sistema cristalino cuyos grupos puntuales tienen más de un sistema reticular asociado a sus grupos espaciales.
El sistema cristalino hexagonal consta de 7 grupos puntuales que tienen un único eje de rotación séxtuple. Estos 7 grupos puntuales tienen 27 grupos espaciales (168 a 194), todos ellos asignados al sistema reticular hexagonal.
Sistema cristalino trigonal
A continuación se enumeran los 5 grupos puntuales de este sistema cristalino, con su número y notación internacionales, sus grupos espaciales en nombre y cristales de ejemplo. [6] [7] [8]
| Grupo espacial no. | Grupo de puntos | Tipo | Ejemplos | Grupos espaciales | |||||
|---|---|---|---|---|---|---|---|---|---|
| Nombre [1] | Internacional | Schoen. | Orbe. | Timonel. | Hexagonal | Romboédrico | |||
| 143–146 | Pirámide trigonal | 3 | C 3 | 33 | [3] + | polar enantiomórfico | carlinita, jarosita | P3, P31 , P32 | R3 |
| 147–148 | Romboédrico | 3 | C3i ( S6 ) | 3× | [2 + ,6 + ] | centrosimétrico | dolomita , ilmenita | Pág. 3 | R3 |
| 149–155 | Trapezoedro trigonal | 32 | D3 | 223 | [2,3] + | enantiomórfico | abhurita , cuarzo alfa (152, 154), cinabrio | P312, P321, P3 1 12, P3 1 21, P3 2 12, P3 2 21 | R32 |
| 156–161 | Pirámide ditrigonal | 3 m | C 3v | *33 | [3] | polar | Schorl , cerita , turmalina , alunita , tantalato de litio | P3m1, P31m, P3c1, P31c | R3m, R3c |
| 162–167 | Escalenoédrico ditrigonal | 3 metros | D 3d | 2*3 | [2 + ,6] | centrosimétrico | antimonio , hematita , corindón , calcita , bismuto | P3 1m , P3 1c , P3 m1 , P3 c1 | R3m , R3c |
Sistema cristalino hexagonal
A continuación se enumeran los 7 grupos de puntos ( clases de cristales ) en este sistema cristalino, seguidos de sus representaciones en notación Hermann-Mauguin o internacional y notación de Schoenflies , y ejemplos minerales , si existen. [2] [9]
| Grupo espacial no. | Grupo de puntos | Tipo | Ejemplos | Grupos espaciales | ||||
|---|---|---|---|---|---|---|---|---|
| Nombre [1] | Internacional | Schoen. | Orbe. | Timonel. | ||||
| 168–173 | Pirámide hexagonal | 6 | C 6 | 66 | [6] + | polar enantiomórfico | nefelina , cancrinita | P6, P6 1 , P6 5 , P6 2 , P6 4 , P6 3 |
| 174 | Bipiramidal trigonal | 6 | C 3 horas | 3* | [2,3 + ] | cesanita , laurelita | Pág. 6 | |
| 175–176 | Bipiramidal hexagonal | 6/m | C 6 horas | 6* | [2,6 + ] | centrosimétrico | apatita , vanadinita | P6/metro, P6 3 /metro |
| 177–182 | Trapezoedro hexagonal | 622 | D6 | 226 | [2,6] + | enantiomórfico | kalsilita , cuarzo beta | P622 , P6122 , P6522 , P6222 , P6422 , P6322 |
| 183–186 | Pirámide dihexagonal | 6 mm | C 6v | *66 | [6] | polar | Greenockita , wurtzita [10] | P6 mm, P6 cc, P6 3 cm, P6 3 mc |
| 187–190 | Bipiramidal ditrigonal | 6m2 | D 3 horas | *223 | [2,3] | benitoíta | P 6 m2, P 6 c2, P 6 2m, P 6 2c | |
| 191–194 | Bipiramidal dihexagonal | 6/mmm | D 6 horas | *226 | [2,6] | centrosimétrico | berilo | P6/mmm, P6/mcc, P6 3 /mcm, P6 3 /mmc |
El volumen de la celda unitaria está dado por 2 c •sin ( 60°)
Empaquetado hexagonal compacto

El empaquetamiento hexagonal compacto (hcp) es uno de los dos tipos simples de empaquetamiento atómico con mayor densidad, siendo el otro el cúbico centrado en las caras (fcc). Sin embargo, a diferencia del fcc, no es una red de Bravais, ya que hay dos conjuntos no equivalentes de puntos de la red. En cambio, se puede construir a partir de la red de Bravais hexagonal utilizando un motivo de dos átomos (el átomo adicional en aproximadamente ( 2 ⁄ 3 , 1 ⁄ 3 , 1 ⁄ 2 )) asociado con cada punto de la red. [11]
Estructuras multielementos
Los compuestos que constan de más de un elemento (por ejemplo, compuestos binarios ) suelen tener estructuras cristalinas basadas en la familia de cristales hexagonales. Aquí se enumeran algunos de los más comunes. Estas estructuras pueden considerarse como dos o más subredes interpenetrantes, donde cada subred ocupa los sitios intersticiales de las otras.
Estructura de la wurtzita



La estructura cristalina de la wurtzita se designa con la designación Strukturbericht B4 y el símbolo de Pearson hP4. El grupo espacial correspondiente es el n.° 186 (en la clasificación de la Unión Internacional de Cristalografía) o P6 3 mc (en la notación de Hermann-Mauguin ). Los símbolos de Hermann-Mauguin en P6 3 mc se pueden leer de la siguiente manera: [13]
- 6 3 .. : una rotación de tornillo de seis vueltas alrededor del eje c
- .m .: un plano de espejo con normal {100}
- ..c : plano de planeo en las direcciones c con normal {120}.
Entre los compuestos que pueden adoptar la estructura de wurtzita se encuentran la propia wurtzita ( ZnS con hasta un 8% de hierro en lugar de zinc ), yoduro de plata (AgI), óxido de zinc (ZnO), sulfuro de cadmio (CdS), seleniuro de cadmio (CdSe), carburo de silicio (α-SiC), nitruro de galio (GaN), nitruro de aluminio (AlN), nitruro de boro (w-BN) y otros semiconductores . [14] En la mayoría de estos compuestos, la wurtzita no es la forma favorecida del cristal a granel, pero la estructura puede verse favorecida en algunas formas nanocristalinas del material.
En materiales con más de una estructura cristalina, a veces se agrega el prefijo "w-" a la fórmula empírica para denotar la estructura cristalina de wurtzita, como en w-BN .
Cada uno de los dos tipos de átomos individuales forma una subred de empaquetamiento hexagonal compacto (tipo HCP). Cuando se observan todos juntos, las posiciones atómicas son las mismas que en la lonsdaleíta ( diamante hexagonal ). Cada átomo está coordinado tetraédricamente . La estructura también se puede describir como una red HCP de zinc con átomos de azufre que ocupan la mitad de los huecos tetraédricos o viceversa.
La estructura de la wurtzita no es centrosimétrica (es decir, carece de simetría de inversión ). Debido a esto, los cristales de wurtzita pueden tener (y generalmente lo hacen) propiedades como piezoelectricidad y piroelectricidad , de las que carecen los cristales centrosimétricos. [ cita requerida ]
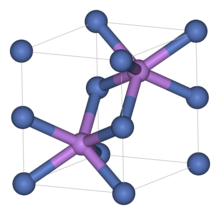
Estructura del arseniuro de níquel
La estructura del arseniuro de níquel consta de dos subredes interpenetrantes: una subred hexagonal primitiva de níquel y una subred hexagonal compacta de arsénico. Cada átomo de níquel está coordinado octaédricamente con seis átomos de arsénico, mientras que cada átomo de arsénico está coordinado prismáticamente trigonalmente con seis átomos de níquel. [15] La estructura también se puede describir como una red HCP de arsénico con níquel ocupando cada vacío octaédrico .
Los compuestos que adoptan la estructura NiAs son generalmente los calcogenuros , arseniuros , antimonuros y bismuturos de los metales de transición . [ cita requerida ]
Los siguientes son los miembros del grupo de la niquelina: [16]
- Achavalita : FeSe
- Breithauptita : NiSb
- Freboldita: CoSe
- Kotulskita: Pd(Te,Bi)
- Langistita: (Co,Ni)As
- Níquel: NiAs
- Sobolevskita: Pd(Bi,Te)
- Sudburyita: (Pd,Ni)Sb
En dos dimensiones
Sólo existe una red de Bravais hexagonal en dos dimensiones: la red hexagonal.
| Celosía de Bravais | Hexagonal |
|---|---|
| Símbolo de Pearson | caballos de fuerza |
| Celda unitaria |  |
Véase también
Referencias
- ^ abcd Hahn, Theo, ed. (2005). Tablas internacionales para cristalografía (5.ª ed.). Dordrecht, Países Bajos: Publicado para la Unión Internacional de Cristalografía por Springer. ISBN 978-0-7923-6590-7.
- ^ ab Dana, James Dwight; Hurlbut, Cornelius Searle (1959). Manual de mineralogía de Dana (17.ª ed.). Nueva York: Chapman Hall. págs. 78–89.
- ^ Edward Prince (2004). Técnicas matemáticas en cristalografía y ciencia de los materiales . Springer Science & Business Media. pág. 41.
- ^ "Diagramas y tablas de grupos espaciales de resolución media". img.chem.ucl.ac.uk .
- ^ Ashcroft, Neil W.; Mermin, N. David (1976). Física del estado sólido (1.ª ed.). Holt, Rinehart y Winston. pág. 119. ISBN 0-03-083993-9.
- ^ Pough, Frederick H.; Peterson, Roger Tory (1998). Una guía de campo para rocas y minerales. Houghton Mifflin Harcourt. pág. 62. ISBN 0-395-91096-X.
- ^ Hurlbut, Cornelius S.; Klein, Cornelis (1985). Manual de mineralogía (20.ª edición). Wiley. Págs. 78-89. ISBN. 0-471-80580-7.
- ^ "Cristalografía y minerales ordenados por forma cristalina". Webmineral .
- ^ "Cristalografía". Webmineral.com . Consultado el 3 de agosto de 2014 .
- ^ "Minerales en el sistema cristalino hexagonal, clase piramidal dihexagonal (6 mm)". Mindat.org . Consultado el 3 de agosto de 2014 .
- ^ Jaswon, Maurice Aaron (1 de enero de 1965). Introducción a la cristalografía matemática. American Elsevier Pub. Co.
- ^ De Graef, Marc; McHenry, Michael E. (2012). Estructura de los materiales: Introducción a la cristalografía, la difracción y la simetría (PDF) . Cambridge University Press. pág. 16.
- ^ Hitchcock, Peter B (1988). Tablas internacionales para cristalografía volumen A.
- ^ Togo, Atsushi; Chaput, Laurent; Tanaka, Isao (20 de marzo de 2015). "Distribuciones de tiempos de vida de fonones en zonas de Brillouin". Physical Review B . 91 (9): 094306. arXiv : 1501.00691 . Código Bibliográfico :2015PhRvB..91i4306T. doi :10.1103/PhysRevB.91.094306. S2CID 118851924.
- ^ Química inorgánica de Duward Shriver y Peter Atkins, 3.ª edición, WH Freeman and Company, 1999, págs. 47, 48.
- ^ http://www.mindat.org/min-2901.html Mindat.org
