Gráfico semilogarítmico


En ciencia e ingeniería , un gráfico semilogarítmico o semilogarítmico tiene un eje en una escala logarítmica y el otro en una escala lineal . Es útil para datos con relaciones exponenciales, donde una variable cubre un amplio rango de valores. [ 1]
Todas las ecuaciones de la forma forman líneas rectas cuando se trazan de forma semilogarítmica, ya que al tomar los logaritmos de ambos lados se obtiene
Se trata de una línea con pendiente y corte vertical. La escala logarítmica suele expresarse en base 10; ocasionalmente, en base 2:
Un gráfico log-lineal (a veces log-lin) tiene la escala logarítmica en el eje y y una escala lineal en el eje x ; un gráfico lineal-log (a veces lin-log) es lo opuesto. La denominación es salida-entrada ( y – x ), el orden opuesto a ( x , y ).
En un gráfico semilogarítmico, el espaciado de la escala en el eje y (o eje x ) es proporcional al logaritmo del número, no al número en sí. Es equivalente a convertir los valores y (o valores x ) a su logaritmo y representar los datos en escalas lineales. Un gráfico logarítmico-logarítmico utiliza la escala logarítmica para ambos ejes y, por lo tanto, no es un gráfico semilogarítmico.
Ecuaciones
La ecuación de una línea en un gráfico logarítmico-lineal, donde el eje de abscisas está escalado logarítmicamente (con una base logarítmica de n ), sería
La ecuación para una línea en un gráfico log-lineal, con un eje de ordenadas escalado logarítmicamente (con una base logarítmica de n ), sería:
Encontrar la función a partir del gráfico semilogarítmico
Gráfica logarítmica lineal
En un gráfico lineal-logarítmico, elija un punto fijo ( x 0 , F 0 ), donde F 0 es la abreviatura de F ( x 0 ), en algún lugar de la línea recta en el gráfico anterior, y además otro punto arbitrario ( x 1 , F 1 ) en el mismo gráfico. La fórmula de pendiente del gráfico es:
Lo que conduce a
o
Lo que significa que
En otras palabras, F es proporcional al logaritmo de x por la pendiente de la línea recta de su gráfico lin-log, más una constante. Específicamente, una línea recta en un gráfico lin-log que contiene los puntos ( F 0 , x 0 ) y ( F 1 , x 1 ) tendrá la función:
gráfico log-lineal
En un gráfico log-lineal (escala logarítmica en el eje y), elija un punto fijo ( x 0 , F 0 ), donde F 0 es la abreviatura de F ( x 0 ), en algún lugar de la línea recta en el gráfico anterior, y además algún otro punto arbitrario ( x 1 , F 1 ) en el mismo gráfico. La fórmula de pendiente del gráfico es:
Lo que conduce a
Observe que n log n ( F 1 ) = F 1 . Por lo tanto, los logaritmos se pueden invertir para encontrar:
o
Esto se puede generalizar para cualquier punto, en lugar de solo F 1 :
Ejemplos del mundo real
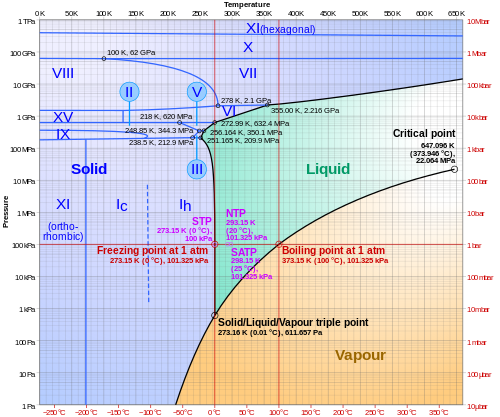
Diagrama de fases del agua
En física y química , se puede utilizar un gráfico del logaritmo de la presión frente a la temperatura para ilustrar las distintas fases de una sustancia, como en el siguiente caso del agua :
La progresión de la "gripe porcina" en 2009
Si bien diez es la base más común , hay ocasiones en que otras bases son más apropiadas, como en este ejemplo: [ se necesita más explicación ]

Observe que, si bien el eje horizontal (tiempo) es lineal, con las fechas espaciadas uniformemente, el eje vertical (casos) es logarítmico, y las divisiones espaciadas uniformemente se etiquetan con potencias sucesivas de dos. El gráfico semilogarítmico permite ver con mayor facilidad cuándo la infección ha dejado de propagarse a su ritmo máximo, es decir, la línea recta en este gráfico exponencial, y comienza a curvarse para indicar un ritmo más lento. Esto podría indicar que alguna forma de acción de mitigación está funcionando, por ejemplo, el distanciamiento social.
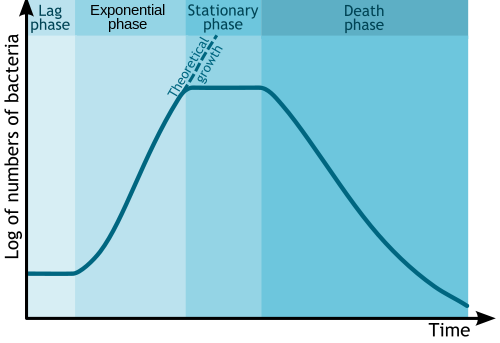
Crecimiento microbiano
En biología e ingeniería biológica , el cambio en la cantidad de microbios debido a la reproducción asexual y al agotamiento de nutrientes se suele ilustrar mediante un gráfico semilogarítmico. El tiempo suele ser el eje independiente, con el logaritmo de la cantidad o masa de bacterias u otros microbios como variable dependiente. Esto forma un gráfico con cuatro fases distintas, como se muestra a continuación.
Véase también
- Nomograma , gráficos más complicados
- Regresión no lineal#Transformación , para convertir una forma no lineal en una forma semilogarítmica susceptible de cálculo no iterativo
- Gráfica logarítmica
Referencias
- ^ (1) Bourne, M. "Gráficos sobre papel logarítmico y semilogarítmico". Interactive Mathematics . www.intmath.com. Archivado desde el original el 6 de agosto de 2021 . Consultado el 26 de octubre de 2021 .
(2) Bourne, Murray (25 de enero de 2007). «Gráfico semilogarítmico interesante: ranking de tráfico de YouTube». SquareCirclez: el blog de IntMath . www.intmath.com. Archivado desde el original el 26 de febrero de 2021. Consultado el 26 de octubre de 2021 .












![{\displaystyle F(x)=(F_{1}-F_{0}){\left[{\frac {\log _{n}(x/x_{0})}{\log _{n}(x_{1}/x_{0})}}\right]}+F_{0}=(F_{1}-F_{0})\log _{\frac {x_{1}}{x_{0}}}{\left({\frac {x}{x_{0}}}\right)}+F_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da143562dac9e25d0e2a741861ef66bb7077d6f6)




