Espacio de color LMS

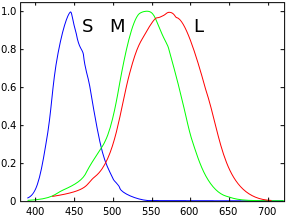
LMS (largo, medio, corto) es un espacio de color que representa la respuesta de los tres tipos de conos del ojo humano , llamados así por sus picos de respuesta (sensibilidad) en longitudes de onda largas, medias y cortas.

El rango numérico no suele especificarse, excepto que el extremo inferior suele estar limitado por cero. Es habitual utilizar el espacio de color LMS cuando se realiza una adaptación cromática (estimación de la apariencia de una muestra bajo un iluminante diferente). También es útil en el estudio del daltonismo , cuando uno o más tipos de conos son defectuosos.

Las funciones de respuesta de cono son las funciones de correspondencia de color para el espacio de color LMS. Las coordenadas de cromaticidad (L, M, S) para una distribución espectral se definen como:${\displaystyle {\bar {l}}(\lambda ),{\bar {m}}(\lambda ),{\bar {s}}(\lambda )}$${\displaystyle J(\lambda )}$

${\displaystyle L=\int _{0}^{\infty }J(\lambda ){\bar {l}}(\lambda )d\lambda }$

${\displaystyle M=\int _{0}^{\infty }J(\lambda ){\bar {m}}(\lambda )d\lambda }$

${\displaystyle S=\int _{0}^{\infty }J(\lambda ){\bar {s}}(\lambda )d\lambda }$

Las funciones de respuesta del cono se normalizan para que sus máximos sean iguales a la unidad.

Por lo general, los colores que se van a adaptar cromáticamente se especificarán en un espacio de color distinto de LMS (por ejemplo, sRGB ). Sin embargo, la matriz de adaptación cromática en el método de transformación de von Kries diagonal opera sobre valores triestímulo en el espacio de color LMS. Dado que los colores en la mayoría de los espacios de color se pueden transformar al espacio de color XYZ , solo se requiere una matriz de transformación adicional para cualquier espacio de color que se vaya a adaptar cromáticamente: transformar colores del espacio de color XYZ al espacio de color LMS. ^[3]

Además, muchos métodos de adaptación de color, o modelos de apariencia de color (CAMs) , ejecutan una transformación matricial diagonal al estilo de von Kries en un espacio ligeramente modificado, similar al LMS. Pueden referirse a él simplemente como LMS, como RGB o como ργβ. El siguiente texto utiliza la denominación "RGB", pero tenga en cuenta que el espacio resultante no tiene nada que ver con el modelo de color aditivo llamado RGB. ^[3]

Se presentan aquí las matrices de transformación de adaptación cromática (CAT) para algunas CAM en términos de coordenadas CIEXYZ . Las matrices, junto con los datos XYZ definidos para el observador estándar , definen implícitamente una respuesta de "cono" para cada tipo de célula.

Notas :

• Todos los valores triestímulo se calculan normalmente utilizando el observador colorimétrico estándar CIE 1931 2° . ^[3]
• A menos que se especifique lo contrario, las matrices CAT están normalizadas (los elementos de una fila suman 1) por lo que los valores triestímulo para un iluminante de igual energía (X=Y=Z), como el iluminante CIE E , producen valores LMS iguales. ^[3]

En este artículo falta información sobre cómo se obtuvo la matriz HPE; parece la más "fisiológica" de las XYZ, pero ¿dónde están los datos? Amplíe el artículo para incluir esta información. Puede que existan más detalles en la página de discusión . ( Octubre de 2021 )

Los modelos de apariencia de color Hunt y RLAB utilizan la matriz de transformación Hunt–Pointer–Estevez ( _MHPE ) para la conversión de CIE XYZ a LMS. ^{[4] [5] [6]} Esta es la matriz de transformación que se utilizó originalmente junto con el método de transformación de von Kries y, por lo tanto, también se denomina matriz de transformación de von Kries (M _vonKries ).

• Iluminadores de igual energía:$${\displaystyle {\begin{bmatrix}L\\M\\S\end{bmatrix}}_{\text{E}}=\left[{\begin{array}{lll}{\phantom {-}}0,38971&{\phantom {-}}0,68898&-0,07868\\-0,22981&{\phantom {-}}1,18340&{\phantom {-}}0,04641\\{\phantom {-}}0&{\phantom {-}}0&{\phantom {-}}1\end{array}}\right]{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}}$$
• Normalizado ^[7] a D65 :$${\displaystyle {\begin{bmatrix}L\\M\\S\end{bmatrix}}_{\text{D65}}=\left[{\begin{array}{lll}{\phantom {-}}0,4002&{\phantom {-}}0,7076&-0,0808\\-0,2263&{\phantom {-}}1,1653&{\phantom {-}}0,0457\\{\phantom {-}}0&{\phantom {-}}0&{\phantom {-}}0,9182\end{array}}\right]{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}}$$

El modelo de apariencia de color original de CIECAM97s utiliza la matriz de transformación de Bradford (MBFD ₎ (al igual que el modelo de apariencia de color de LLAB ). ^[3] Esta es una matriz de transformación “espectralmente agudizada” (es decir, las curvas de respuesta de los conos L y M son más estrechas y más distintas entre sí). Se suponía que la matriz de transformación de Bradford funcionaría junto con un método de transformación de von Kries modificado que introdujo una pequeña no linealidad en el canal S (azul). Sin embargo, fuera de CIECAM97s y LLAB esto a menudo se descuida y la matriz de transformación de Bradford se utiliza junto con el método de transformación de von Kries lineal, explícitamente en los perfiles ICC . ^[8]$${\displaystyle {\begin{bmatrix}R\\G\\B\end{bmatrix}}_{\text{BFD}}=\left[{\begin{array}{lll}{\phantom {-}}0,8951&{\phantom {-}}0,2664&-0,1614\\-0,7502&{\phantom {-}}1,7135&{\phantom {-}}0,0367\\{\phantom {-}}0,0389&-0,0685&{\phantom {-}}1,0296\end{array}}\right]{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}}$$

Se cree que una matriz "espectralmente nítida" mejora la adaptación cromática, especialmente para los colores azules, pero no funciona como un espacio LMS de descripción de conos real para el posterior procesamiento de la visión humana. Aunque los resultados se denominan "LMS" en la versión LLAB original, CIECAM97s utiliza un nombre "RGB" diferente para destacar que este espacio no refleja realmente las células cónicas; de ahí los diferentes nombres aquí.

LLAB procede a tomar los valores XYZ posteriores a la adaptación y realiza un tratamiento similar al de CIELAB para obtener los correlatos visuales. Por otro lado, CIECAM97s toma el valor XYZ posterior a la adaptación y lo vuelve a introducir en el espacio LMS de Hunt, y trabaja a partir de ahí para modelar el cálculo de las propiedades del color del sistema de visión.

Una versión revisada de CIECAM97s vuelve a un método de transformación lineal e introduce una matriz de transformación correspondiente (M _CAT97s ): ^[9]$${\displaystyle {\begin{bmatrix}R\\G\\B\end{bmatrix}}_{\text{97}}=\left[{\begin{array}{lll}{\phantom {-}}0,8562&{\phantom {-}}0,3372&-0,1934\\-0,8360&{\phantom {-}}1,8327&{\phantom {-}}0,0033\\{\phantom {-}}0,0357&-0,0469&{\phantom {-}}1,0112\end{array}}\right]{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}}$$

La matriz de transformación agudizada en CIECAM02 (M _CAT02 ) es: ^{[10] [3]}$${\displaystyle {\begin{bmatrix}R\\G\\B\end{bmatrix}}_{\text{02}}=\left[{\begin{array}{lll}{\phantom {-}}0.7328&{\phantom {-}}0.4296&-0.1624\\-0.7036&{\phantom {-}}1.6975&{\phantom {-}}0.0061\\{\phantom {-}}0.0030&{\phantom {-}}0.0136&{\phantom {-}}0.9834\end{array}}\right]{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}}$$

CAM16 utiliza una matriz diferente: ^[11]$${\displaystyle {\begin{bmatrix}R\\G\\B\end{bmatrix}}_{\text{16}}=\left[{\begin{array}{lll}{\phantom {-}}0.401288&{\phantom {-}}0.650173&-0.051461\\-0.250268&{\phantom {-}}1.204414&{\phantom {-}}0.045854\\-0.002079&{\phantom {-}}0.048952&{\phantom {-}}0.953127\end{array}}\right]{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}}$$

Al igual que en CIECAM97, después de la adaptación, los colores se convierten al LMS tradicional Hunt–Pointer–Estévez para la predicción final de los resultados visuales.

Desde un punto de vista fisiológico, el espacio de color LMS describe un nivel más fundamental de respuesta visual humana, por lo que tiene más sentido definir el XYZ fisiopsicológico por LMS, en lugar de al revés.

En 2000, Stockman y Sharpe propusieron un conjunto de funciones LMS basadas en la fisiología. Las funciones se publicaron en un informe técnico de la CIE en 2006 (CIE 170). ^{[12] [13]} Las funciones se derivan de los datos CMF RGB de Stiles y Burch ^[1] , combinados con mediciones más recientes sobre la contribución de cada cono en las funciones RGB. Para ajustar los datos de 10° a 2°, se utilizan suposiciones sobre la diferencia de densidad de fotopigmentos y datos sobre la absorción de luz por el pigmento en el cristalino y la mácula lútea . ^[14]

Las funciones Stockman y Sharpe pueden luego convertirse en un conjunto de tres funciones de coincidencia de colores similares a las funciones CIE 1931. ^[15]

Sean las tres funciones de respuesta del cono y sean las nuevas funciones de coincidencia de color XYZ. Entonces, por definición, las nuevas funciones de coincidencia de color XYZ son:${\displaystyle {\mathcal {P}}_{i}(\lambda )=({\bar {l}}(\lambda ),{\bar {m}}(\lambda ),{\bar {s}}(\lambda ))}$${\displaystyle {\mathcal {Q}}_{i}(\lambda )=({\bar {x}}_{\text{F}}(\lambda ),{\bar {y}}_{\text{F}}(\lambda ),{\bar {z}}_{\text{F}}(\lambda ))}$

${\displaystyle {\mathcal {Q}}_{i}(\lambda )=\sum _{j=1}^{3}T_{ij}{\mathcal {P}}_{j}(\lambda )}$

donde la matriz de transformación se define como:${\displaystyle T_{ij}}$$${\displaystyle T_{ij}=\left[\,{\begin{array}{lll}1.94735469&-1.41445123&{\phantom {-}}0.36476327\\0.68990272&{\phantom {-}}0.34832189&{\phantom {-}}0\\0&{\phantom {-}}0&{\phantom {-}}1.93485343\end{array}}\right]}$$

La derivación de esta transformación es relativamente sencilla. ^[16] La CMF es la función de eficiencia luminosa propuesta originalmente por Sharpe et al. (2005), ^[17] pero luego corregida (Sharpe et al., 2011 ^{[18] [a]} ). La CMF es igual a la fundamental del cono propuesta originalmente por Stockman, Sharpe y Fach (1999) ^[19] escalada para tener una integral igual a la CMF. La definición de la CMF se deriva de las siguientes restricciones:${\displaystyle {\bar {y}}_{\text{F}}(\lambda )}$${\displaystyle {\bar {z}}_{\text{F}}(\lambda )}$${\displaystyle {\bar {s}}(\lambda )}$${\displaystyle {\bar {y}}_{\text{F}}(\lambda )}$${\displaystyle {\bar {x}}_{\text{F}}(\lambda )}$

1. Al igual que los otros CMF, los valores de son todos positivos.${\displaystyle {\bar {x}}_{\text{F}}(\lambda )}$
2. La integral de es idéntica a las integrales de y .${\displaystyle {\bar {x}}_{\text{F}}(\lambda )}$${\displaystyle {\bar {y}}_{\text{F}}(\lambda )}$${\displaystyle {\bar {z}}_{\text{F}}(\lambda )}$
3. Los coeficientes de la transformación obtenida se optimizan para minimizar las diferencias euclidianas entre las funciones de coincidencia de color y resultantes y las funciones de coincidencia de color y de CIE 1931 .${\displaystyle {\bar {x}}_{\text{F}}(\lambda )}$${\displaystyle {\bar {x}}_{\text{F}}(\lambda )}$${\displaystyle {\bar {y}}_{\text{F}}(\lambda )}$${\displaystyle {\bar {z}}_{\text{F}}(\lambda )}$${\displaystyle {\bar {x}}(\lambda )}$${\displaystyle {\bar {y}}(\lambda )}$${\displaystyle {\bar {z}}(\lambda )}$
   — Descripción CVRL para 'Funciones de coincidencia de color "fisiológicamente relevantes" de 2 grados XYZ de CIE (2012)' ^[15]

Para cualquier distribución espectral , sean las coordenadas de cromaticidad LMS para y sean las nuevas coordenadas de cromaticidad XYZ correspondientes. Entonces:${\displaystyle J(\lambda )}$${\displaystyle P_{i}=(L,M,S)}$${\displaystyle J(\lambda )}$${\displaystyle Q_{i}=(X,Y,Z)_{\text{F}}}$

${\displaystyle Q_{i}=\int _{0}^{\infty }J(\lambda ){\mathcal {Q}}_{i}(\lambda )d\lambda =\int _{0}^{\infty }J(\lambda )\sum _{j=1}^{3}T_{ij}{\mathcal {P}}_{j}(\lambda )d\lambda =\sum _{j=1}^{3}T_{ij}P_{j}}$

o, explícitamente:$${\displaystyle {\begin{bmatrix}X\\Y\\Z\end{bmatrix}}_{\text{F}}=\left[\,{\begin{array}{lll}1.94735469&-1.41445123&{\phantom {-}}0.36476327\\0.68990272&{\phantom {-}}0.34832189&{\phantom {-}}0\\0&{\phantom {-}}0&{\phantom {-}}1.93485343\end{array}}\right]{\begin{bmatrix}L\\M\\S\end{bmatrix}}}$$

La matriz inversa se muestra aquí para compararla con las del XYZ tradicional:$${\displaystyle {\begin{bmatrix}L\\M\\S\end{bmatrix}}=\left[{\begin{array}{lll}{\phantom {-}}0.210576&{\phantom {-}}0.855098&-0.0396983\\-0.417076&{\phantom {-}}1.177260&{\phantom {-}}0.0786283\\{\phantom {-}}0&{\phantom {-}}0&{\phantom {-}}0.5168350\\\end{array}}\right]{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}_{\text{F}}}$$

El desarrollo anterior tiene la ventaja de basar las nuevas funciones de correspondencia de color X _F Y _F Z _{F en las funciones de respuesta del cono LMS basadas en la fisiología. Además, ofrece una relación uno a uno entre las coordenadas de cromaticidad LMS y las nuevas coordenadas de cromaticidad X F} Y _F Z _F , lo que no era el caso para las funciones de correspondencia de color CIE 1931. La transformación para un color particular entre LMS y el espacio XYZ CIE 1931 no es única. Más bien depende en gran medida de la forma particular de la distribución espectral que produce el color dado. No existe una matriz fija de 3x3 que transforme entre las coordenadas XYZ CIE 1931 y las coordenadas LMS, incluso para un color particular, y mucho menos para toda la gama de colores. Cualquier transformación de este tipo será una aproximación en el mejor de los casos, y generalmente requerirá ciertas suposiciones sobre las distribuciones espectrales que producen el color. Por ejemplo, si las distribuciones espectrales se limitan a ser el resultado de mezclar tres fuentes monocromáticas (como se hizo en la medición de las funciones de correspondencia de color CIE 1931 y Stiles y Burch ^[1] ), entonces habrá una relación uno a uno entre las coordenadas XYZ LMS y CIE 1931 de un color en particular.${\displaystyle J(\lambda )}$

Al 28 de noviembre de 2023, los CMF CIE 170-2 son propuestas que aún deben ser ratificadas por el comité TC 1-36 en pleno o por la CIE.

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (June 2024) (Learn how and when to remove this message)

Para fines teóricos, suele ser conveniente caracterizar la radiación en términos de fotones en lugar de energía. La energía E de un fotón viene dada por la relación de Planck.

${\displaystyle E=h\nu =hc/\lambda }$

donde E es la energía por fotón, h es la constante de Planck , c es la velocidad de la luz , ν es la frecuencia de la radiación y λ es la longitud de onda. Una cantidad radiativa espectral en términos de energía, JE ( λ ), se convierte a su forma cuántica JQ ( λ ) dividiendo por la energía por fotón:

${\displaystyle JQ(\lambda )=JE(\lambda )(\lambda /hc)}$

Por ejemplo, si JE ( λ ) es radiancia espectral con la unidad W/m ² /sr/m, entonces el equivalente cuántico JQ ( λ ) caracteriza esa radiación con la unidad fotones/s/m ² /sr/m.

Si CE _λi ( λ ) ( i =1,2,3) son las tres funciones de correspondencia de color basadas en energía para un espacio de color particular (espacio de color LMS para los fines de este artículo), entonces los valores triestímulo se pueden expresar en términos de la cantidad radiativa cuántica mediante:

${\displaystyle CE_{i}=\int _{0}^{\infty }JE(\lambda )CE_{\lambda i}(\lambda )d\lambda =\int _{0}^{\infty }JQ(\lambda )(hc/\lambda )CE_{\lambda i}(\lambda )d\lambda }$

Defina las funciones de correspondencia de colores cuánticos:

${\displaystyle CQ_{\lambda i}(\lambda )=(CE_{\lambda i}(\lambda )/\lambda )/(CE_{\lambda i}(\lambda _{i\,{\text{max}}})/\lambda _{i\,{\text{max}}})}$

donde λ _{i max} es la longitud de onda en la que CE _{λ i} ( λ )/ λ se maximiza. Defina los valores triestímulo cuánticos:

${\displaystyle CQ_{i}=\int _{0}^{\infty }JQ(\lambda )CQ_{\lambda i}(\lambda )d\lambda }$

Tenga en cuenta que, al igual que con las funciones basadas en energía, el valor pico de CQ _λi ( λ ) será igual a la unidad. Utilizando la ecuación anterior para los valores triestímulo de energía CE _i

${\displaystyle CE_{i}=(hc/\lambda _{i\,max})\,CE_{\lambda i}(\lambda _{i\,max})\,CQ_{i}}$

Para el espacio de color LMS, ≈ {566, 541, 441} nm y ${\displaystyle \lambda _{i\,{\text{max}}}}$

${\displaystyle CE_{i}/CQ_{i}=\{3.49694,3.1253,0.144944\}\times 10^{-19}}$J/fotón

El espacio de color LMS se puede utilizar para emular la forma en que las personas daltónicas ven el color. Brettel et al. (1997) produjeron una primera emulación de dicromáticos que fue valorada favorablemente por pacientes reales. Un ejemplo de un método de última generación es el de Machado et al. (2009). ^[20]

Una aplicación relacionada es la creación de filtros de color para que las personas daltónicas puedan notar más fácilmente las diferencias de color, un proceso conocido como daltonización . ^[21]

JPEG XL utiliza un espacio de color XYB derivado de LMS. Su matriz de transformación se muestra aquí:$${\displaystyle {\begin{bmatrix}X\\Y\\B\end{bmatrix}}={\begin{bmatrix}1&-1&{\phantom {-}}0\\1&{\phantom {-}}1&{\phantom {-}}0\\0&{\phantom {-}}0&{\phantom {-}}1\end{bmatrix}}{\begin{bmatrix}L\\M\\S\end{bmatrix}}}$$

Esto puede interpretarse como una teoría de color híbrida donde L y M son oponentes pero S se maneja de manera tricromática, justificada por la menor densidad espacial de los conos S. En términos prácticos, esto permite utilizar menos datos para almacenar señales azules sin perder mucha calidad percibida. ^[22]

El espacio de color se origina en la métrica butteraugli de Guetzli , ^[23] y se transmitió a JPEG XL a través del proyecto Pik de Google.

• Balance de color
• Visión del color
• Función de eficiencia luminosa
• Tricromacia