Beta termodinámica

En termodinámica estadística , la beta termodinámica , también conocida como frialdad , ^[1] es el recíproco de la temperatura termodinámica de un sistema: (donde T es la temperatura y k _B es la constante de Boltzmann ). ^[2]$${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}}$$

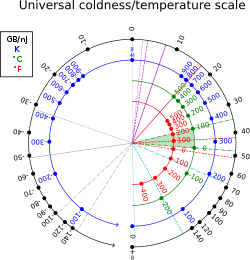
La beta termodinámica tiene unidades recíprocas a las de la energía (en unidades del SI , julios recíprocos , ). En unidades no térmicas, también se puede medir en bytes por julio, o más convenientemente, gigabytes por nanojulio; ^[3] 1 K ⁻¹ es equivalente a aproximadamente 13.062 gigabytes por nanojulio; a temperatura ambiente: T = 300 K, β ≈${\displaystyle [\beta ]={\textrm {J}}^{-1}}$44 GB/nJ ≈39  eV ⁻¹ ≈2,4 × 10 ²⁰  J ⁻¹ . El factor de conversión es 1 GB/nJ = J ⁻¹ .${\displaystyle 8\ln 2\times 10^{18}}$

La beta termodinámica es esencialmente la conexión entre la teoría de la información y la interpretación de la mecánica estadística de un sistema físico a través de su entropía y la termodinámica asociada con su energía . Expresa la respuesta de la entropía a un aumento de energía. Si se agrega una pequeña cantidad de energía al sistema, entonces β describe la cantidad en que el sistema se aleatorizará.

A través de la definición estadística de la temperatura como función de la entropía, la función de frío se puede calcular en el conjunto microcanónico a partir de la fórmula

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}\,={\frac {1}{k_{\rm {B}}}}\left({\frac {\partial S}{\partial E}}\right)_{V,N}}$

(es decir, la derivada parcial de la entropía S con respecto a la energía E a volumen constante V y número de partículas N ).

Aunque es completamente equivalente en contenido conceptual a la temperatura, β generalmente se considera una cantidad más fundamental que la temperatura debido al fenómeno de temperatura negativa , en el que β es continua cuando cruza cero mientras que T tiene una singularidad. ^[4]

Además, β tiene la ventaja de ser más fácil de entender causalmente: si se añade una pequeña cantidad de calor a un sistema, β es el aumento de entropía dividido por el aumento de calor. La temperatura es difícil de interpretar en el mismo sentido, ya que no es posible "añadir entropía" a un sistema excepto de forma indirecta, modificando otras magnitudes como la temperatura, el volumen o el número de partículas.

Desde el punto de vista estadístico, β es una cantidad numérica que relaciona dos sistemas macroscópicos en equilibrio. La formulación exacta es la siguiente. Considérese dos sistemas, 1 y 2, en contacto térmico, con energías respectivas E ₁ y E ₂ . Suponemos que E ₁ + E ₂ = alguna constante E . El número de microestados de cada sistema se denotará por Ω ₁ y Ω ₂ . Bajo nuestras suposiciones, Ω _i depende solo de E _i . También suponemos que cualquier microestado del sistema 1 consistente con E ₁ puede coexistir con cualquier microestado del sistema 2 consistente con E ₂ . Por lo tanto, el número de microestados para el sistema combinado es

${\displaystyle \Omega =\Omega _{1}(E_{1})\Omega _{2}(E_{2})=\Omega _{1}(E_{1})\Omega _{2}( E-E_{1}).\,}$

Derivaremos β del supuesto fundamental de la mecánica estadística :

Cuando el sistema combinado alcanza el equilibrio, el número Ω se maximiza.

(En otras palabras, el sistema busca naturalmente el número máximo de microestados). Por lo tanto, en equilibrio,

${\displaystyle {\frac {d}{dE_{1}}}\Omega =\Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})+\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})\cdot {\frac {dE_{2}}{dE_{1}}}=0.}$

Pero E ₁ + E ₂ = E implica

${\displaystyle {\frac {dE_{2}}{dE_{1}}}=-1.}$

Entonces

${\displaystyle \Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})-\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})=0}$

es decir

${\displaystyle {\frac {d}{dE_{1}}}\ln \Omega _{1}={\frac {d}{dE_{2}}}\ln \Omega _{2}\quad {\mbox{at equilibrium.}}}$

La relación anterior motiva una definición de β :

${\displaystyle \beta ={\frac {d\ln \Omega }{dE}}.}$

Cuando dos sistemas están en equilibrio, tienen la misma temperatura termodinámica T . Por lo tanto, intuitivamente, se esperaría que β (tal como se define a través de microestados) esté relacionada con T de alguna manera. Este vínculo lo proporciona el supuesto fundamental de Boltzmann escrito como

${\displaystyle S=k_{\rm {B}}\ln \Omega ,}$

donde k _B es la constante de Boltzmann , S es la entropía termodinámica clásica y Ω es el número de microestados.

${\displaystyle d\ln \Omega ={\frac {1}{k_{\rm {B}}}}dS.}$

Sustituyendo en la definición de β la definición estadística anterior se obtiene

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}}}{\frac {dS}{dE}}.}$

Comparando con la fórmula termodinámica

${\displaystyle {\frac {dS}{dE}}={\frac {1}{T}},}$

tenemos

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}={\frac {1}{\tau }}}$

donde se llama temperatura fundamental del sistema, y ​​tiene unidades de energía.${\displaystyle \tau }$

This section's factual accuracy is disputed. Relevant discussion may be found on the talk page. Please help to ensure that disputed statements are reliably sourced. (September 2024) (Learn how and when to remove this message)

La beta termodinámica fue introducida originalmente en 1971 (como Kältefunktion "función de frío") por Ingo Müller  [de] , uno de los defensores de la escuela de pensamiento de la termodinámica racional , ^{[5] [6]} basándose en propuestas anteriores de una función de "temperatura recíproca". ^{[1] [7] [ se necesita una fuente no primaria ]}

• Distribución de Boltzmann
• Conjunto canónico
• Modelo de Ising