Problema de flujo máximo

En la teoría de optimización , los problemas de flujo máximo implican encontrar un flujo factible a través de una red de flujo que obtenga el máximo caudal posible.

El problema del flujo máximo puede verse como un caso especial de problemas de flujo de red más complejos, como el problema de circulación . El valor máximo de un flujo st (es decir, flujo desde la fuente s hasta el sumidero t) es igual a la capacidad mínima de un corte st (es decir, corte que separa s de t) en la red, como se indica en el teorema de flujo máximo y corte mínimo .

El problema del flujo máximo fue formulado por primera vez en 1954 por TE Harris y FS Ross como un modelo simplificado del flujo de tráfico ferroviario soviético. ^{[1] [2] [3]}

En 1955, Lester R. Ford, Jr. y Delbert R. Fulkerson crearon el primer algoritmo conocido, el algoritmo Ford-Fulkerson . ^{[4] [5]} En su artículo de 1955, ^[4] Ford y Fulkerson escribieron que el problema de Harris y Ross se formula de la siguiente manera (ver ^[1] p. 5):

Consideremos una red ferroviaria que conecta dos ciudades a través de una serie de ciudades intermedias, donde cada enlace de la red tiene un número asignado que representa su capacidad. Suponiendo una condición de estado estable, encuentre un flujo máximo desde una ciudad dada a la otra.

En su libro Flows in Network , ^[5] en 1962, Ford y Fulkerson escribieron:

Fue planteado a los autores en la primavera de 1955 por TE Harris, quien, junto con el general FS Ross (retirado), había formulado un modelo simplificado del flujo de tráfico ferroviario y señaló este problema particular como el central sugerido por el modelo [11].

donde [11] se refiere al informe secreto de 1955 Fundamentos de un método para evaluar las capacidades de la red ferroviaria de Harris y Ross ^[3] (véase ^[1] pág. 5).

A lo largo de los años, se descubrieron varias soluciones mejoradas al problema del flujo máximo, en particular el algoritmo de ruta de aumento más corta de Edmonds y Karp e independientemente de Dinitz; el algoritmo de flujo de bloqueo de Dinitz; el algoritmo push-relabel de Goldberg y Tarjan ; y el algoritmo de flujo de bloqueo binario de Goldberg y Rao. Los algoritmos de Sherman ^[6] y Kelner, Lee, Orecchia y Sidford, ^{[7] [8]} respectivamente, encuentran un flujo máximo aproximadamente óptimo pero solo funcionan en grafos no dirigidos.

En 2013, James B. Orlin publicó un artículo que describe un algoritmo. ^[9]${\displaystyle O(|V||E|)}$

En 2022, Li Chen, Rasmus Kyng, Yang P. Liu, Richard Peng, Maximilian Probst Gutenberg y Sushant Sachdeva publicaron un algoritmo de tiempo casi lineal que se ejecuta en el problema de flujo de costo mínimo , del cual el problema de flujo máximo es un caso particular. ^{[10] [11]} Para el problema de la ruta más corta de una sola fuente (SSSP) con pesos negativos, también se ha informado de otro caso particular de problema de flujo de costo mínimo: un algoritmo en tiempo casi lineal. ^{[12] [13] Ambos algoritmos fueron considerados los mejores artículos en el} Simposio sobre Fundamentos de la Ciencia de la Computación de 2022. ^{[14] [15]}${\displaystyle O(|E|^{1+o(1)})}$

Primero establecemos alguna notación:

• Sea una red con siendo la fuente y el sumidero de respectivamente.${\displaystyle N=(V,E)}$${\displaystyle s,t\en V}$${\estilo de visualización N}$
• Si es una función en los bordes de entonces su valor en se denota por o${\estilo de visualización g}$${\estilo de visualización N}$${\displaystyle (u,v)\en E}$${\displaystyle g_{uv}}$${\displaystyle g(u,v).}$

Definición. La capacidad de un borde es la cantidad máxima de flujo que puede pasar a través de un borde. Formalmente es un mapa.${\displaystyle c:E\to \mathbb {R} ^{+}.}$

Definición. Un flujo es un mapa que cumple con lo siguiente:${\displaystyle f:E\to \mathbb {R} }$

• Restricción de capacidad . El flujo de un borde no puede exceder su capacidad, en otras palabras: para todos${\displaystyle f_{uv}\leq c_{uv}}$${\displaystyle (u,v)\in E.}$
• Conservación de flujos. La suma de los flujos que entran en un nodo debe ser igual a la suma de los flujos que salen de ese nodo, excepto el de origen y el de destino. O bien:

${\displaystyle \forall v\in V\setminus \{s,t\}:\quad \sum _{u:(u,v)\in E,f_{uv}>0}f_{uv}=\sum _{u:(v,u)\in E,f_{vu}>0}f_{vu}.}$

Observación . Los flujos son asimétricos: para todos${\displaystyle f_{uv}=-f_{vu}}$${\displaystyle (u,v)\in E.}$

Definición. El valor del caudal es la cantidad de flujo que pasa desde la fuente hasta el sumidero. Formalmente, para un caudal, viene dado por:${\displaystyle f:E\to \mathbb {R} ^{+}}$

${\displaystyle |f|=\sum _{v:\ (s,v)\in E}f_{sv}=\sum _{u:\ (u,t)\in E}f_{ut}.}$

Definición. El problema del caudal máximo consiste en dirigir la mayor cantidad de caudal posible desde la fuente hasta el sumidero, es decir, encontrar el caudal con valor máximo.${\displaystyle f_{\textrm {max}}}$

Obsérvese que pueden existir varios caudales máximos y, si se permiten valores reales arbitrarios (o incluso racionales arbitrarios) de caudal (en lugar de solo números enteros), existe exactamente un caudal máximo o infinitos, ya que existen infinitas combinaciones lineales de los caudales máximos de base. En otras palabras, si enviamos unidades de caudal en el borde en un caudal máximo y unidades de caudal en en otro caudal máximo, entonces para cada uno podemos enviar unidades en y enrutar el flujo en los bordes restantes en consecuencia, para obtener otro caudal máximo. Si los valores de caudal pueden ser cualquier número real o racional, entonces existen infinitos valores de este tipo para cada par .${\displaystyle x}$${\displaystyle u}$${\displaystyle y>x}$${\displaystyle u}$${\displaystyle \Delta \in [0,y-x]}$${\displaystyle x+\Delta }$${\displaystyle u}$${\displaystyle \Delta }$${\displaystyle x,y}$

La siguiente tabla enumera algoritmos para resolver el problema de flujo máximo. Aquí, y denotan el número de vértices y aristas de la red. El valor se refiere a la capacidad de arista más grande después de reescalar todas las capacidades a valores enteros (si la red contiene capacidades irracionales , puede ser infinita).${\displaystyle V}$${\displaystyle E}$${\displaystyle U}$${\displaystyle U}$

Método	Año	Complejidad	Descripción
Programación lineal			Restricciones dadas por la definición de un flujo legal . Vea el programa lineal aquí.
Algoritmo de Ford-Fulkerson	1955	${\displaystyle O(EU)}$	Mientras haya un camino abierto a través del gráfico residual, envíe el mínimo de las capacidades residuales en ese camino.
Algoritmo de Edmonds-Karp	1970	${\displaystyle O(VE^{2})}$	Una especialización de Ford–Fulkerson, encontrar caminos de aumento con búsqueda en amplitud .
Algoritmo de Dinic	1970	${\displaystyle O(V^{2}E)}$	En cada fase, el algoritmo construye un gráfico en capas con búsqueda en amplitud en el gráfico residual . El caudal máximo en un gráfico en capas se puede calcular en tiempo y el número máximo de fases es . En redes con capacidades unitarias, el algoritmo de Dinic termina en el tiempo.${\displaystyle O(VE)}$${\displaystyle V-1}$${\displaystyle O(\min\{V^{2/3},E^{1/2}\}E)}$
Algoritmo MKM (Malhotra, Kumar, Maheshwari) [16]	1978	${\displaystyle O(V^{3})}$	Una modificación del algoritmo de Dinic con un enfoque diferente para construir flujos de bloqueo. Consulte el artículo original.
Algoritmo de Dinic con árboles dinámicos	1983	${\displaystyle O(VE\log V)}$	La estructura de datos de árboles dinámicos acelera el cálculo del flujo máximo en el gráfico en capas .${\displaystyle O(VE\log V)}$
Algoritmo general de inserción y reetiquetado [17]	1986	${\displaystyle O(V^{2}E)}$	El algoritmo push reetiquetado mantiene un preflujo, es decir, una función de flujo con posibilidad de exceso en los vértices. El algoritmo se ejecuta mientras haya un vértice con exceso positivo, es decir, un vértice activo en el grafo. La operación push aumenta el flujo en una arista residual, y una función de altura en los vértices controla a través de qué aristas residuales se puede empujar el flujo. La función de altura se modifica mediante la operación reetiquetado. Las definiciones adecuadas de estas operaciones garantizan que la función de flujo resultante sea un flujo máximo.
Algoritmo de inserción y reetiquetado con regla de selección de vértices FIFO [17]	1988	${\displaystyle O(V^{3})}$	Variante del algoritmo push-relabel que siempre selecciona el vértice activo más recientemente y realiza operaciones push mientras el exceso sea positivo y haya aristas residuales admisibles de este vértice.
Algoritmo de inserción y reetiquetado con regla de selección de vértices de distancia máxima [18]	1988	${\displaystyle O(V^{2}{\sqrt {E}})}$	Variante del algoritmo push-relabel que siempre selecciona el vértice más distante de o (es decir, el vértice de etiqueta más alto) pero por lo demás procede como el algoritmo FIFO.${\displaystyle s}$${\displaystyle t}$
Algoritmo push-relabel con árboles dinámicos [17]	1988	${\displaystyle O\left(VE\log {\frac {V^{2}}{E}}\right)}$	El algoritmo construye árboles de tamaño limitado en el gráfico residual en relación con la función de altura. Estos árboles proporcionan operaciones de empuje de varios niveles, es decir, empujan a lo largo de toda una ruta de saturación en lugar de un solo borde.
Algoritmo de KRT (King, Rao, Tarjan) [19]	1994	${\displaystyle O\left(VE\log _{\frac {E}{V\log V}}V\right)}$
Algoritmo de flujo de bloqueo binario [20]	1998	${\displaystyle O\left(E\cdot \min\{V^{2/3},E^{1/2}\}\cdot \log {\frac {V^{2}}{E}}\cdot \log U\right)}$
Algoritmo de James B Orlin + KRT (King, Rao, Tarjan) [9]	2013	${\displaystyle O(VE)}$	El algoritmo de Orlin resuelve el flujo máximo en el tiempo para mientras que KRT lo resuelve en para .${\displaystyle O(VE)}$${\displaystyle E\leq O(V^{{\frac {16}{15}}-\epsilon })}$${\displaystyle O(VE)}$${\displaystyle E>V^{1+\epsilon }}$
Algoritmo de Kathuria-Liu-Sidford [21]	2020	${\displaystyle E^{4/3+o(1)}U^{1/3}}$	Métodos de puntos interiores y refuerzo de bordes mediante flujos de norma. Se basa en un algoritmo anterior de Madry, que logró un tiempo de ejecución de . [22]${\displaystyle \ell _{p}}$${\displaystyle {\tilde {O}}(E^{10/7}U^{1/7})}$
Algoritmo BLNPSSSW / BLLSSSW [23] [24]	2020	${\displaystyle {\tilde {O}}((E+V^{3/2})\log U)}$	Métodos de puntos interiores y mantenimiento dinámico de flujos eléctricos con descomposiciones de expansores.
Algoritmo de Gao-Liu-Peng [25]	2021	${\displaystyle {\tilde {O}}(E^{{\frac {3}{2}}-{\frac {1}{328}}}\log U)}$	El algoritmo de Gao, Liu y Peng gira en torno al mantenimiento dinámico de los flujos eléctricos crecientes en el núcleo del algoritmo basado en el método del punto interior de [Mądry JACM '16]. Esto implica diseñar estructuras de datos que, en entornos limitados, devuelvan bordes con gran energía eléctrica en un gráfico que experimenta actualizaciones de resistencia.
Algoritmo de Chen, Kyng, Liu, Peng, Gutenberg y Sachdeva [10]	2022	${\displaystyle O(E^{1+o(1)}\log U)}$ La complejidad exacta no se indica claramente en el documento, pero parece ser${\displaystyle E\exp O(\log ^{7/8}E\log \log E)\log U}$	El algoritmo de Chen, Kyng, Liu, Peng, Gutenberg y Sachdeva resuelve el flujo máximo y el flujo de costo mínimo en un tiempo casi lineal construyendo el flujo a través de una secuencia de ciclos aproximados de relación mínima no dirigidos, cada uno de los cuales se calcula y procesa en tiempo amortizado utilizando una estructura de datos dinámica.${\displaystyle E^{1+o(1)}}$${\displaystyle E^{o(1)}}$
Bernstein, Blikstad, Saranurak, Tu [26]	2024	${\displaystyle O(n^{2+o(1)}\log U)}$Algoritmo aleatorio cuando las capacidades de borde provienen del conjunto${\displaystyle \{1,\dots ,U\}}$	El algoritmo es una variante del algoritmo push-relabel que introduce la variante ponderada . El artículo establece una función de peso en gráficos dirigidos y acíclicos (DAG), e intenta imitarla en gráficos generales utilizando jerarquías de expansores dirigidos, que inducen un ordenamiento de vértices natural que produce la función de peso similar a la del caso especial de DAG. El aspecto de aleatorización (y, posteriormente, el factor) proviene de la dificultad de aplicar jerarquías de expansores dirigidos al cálculo de cortes dispersos , que no permiten una actualización dinámica natural.${\displaystyle n^{o(1)}}$

Para algoritmos adicionales, consulte Goldberg y Tarjan (1988).

El teorema de flujo integral establece que

Si cada borde de una red de flujo tiene capacidad integral, entonces existe un flujo máximo integral.

La afirmación no es sólo que el valor del flujo es un entero, lo que se desprende directamente del teorema de flujo máximo y corte mínimo , sino que el flujo en cada arista es entero. Esto es crucial para muchas aplicaciones combinatorias (ver más abajo), donde el flujo a través de una arista puede codificar si el elemento correspondiente a esa arista debe incluirse en el conjunto buscado o no.

Dada una red con un conjunto de fuentes y un conjunto de sumideros en lugar de solo una fuente y un sumidero, debemos encontrar el flujo máximo a través de . Podemos transformar el problema de múltiples fuentes y múltiples sumideros en un problema de flujo máximo agregando una fuente consolidada que se conecta a cada vértice en y un sumidero consolidado conectado por cada vértice en (también conocido como superfuente y supersumidero ) con capacidad infinita en cada borde (ver Figura 4.1.1).${\displaystyle N=(V,E)}$${\displaystyle S=\{s_{1},\ldots ,s_{n}\}}$${\displaystyle T=\{t_{1},\ldots ,t_{m}\}}$${\displaystyle N}$${\displaystyle S}$${\displaystyle T}$

Dado un grafo bipartito , debemos encontrar una correspondencia de cardinalidad máxima en , es decir, una correspondencia que contenga el mayor número posible de aristas. Este problema se puede transformar en un problema de flujo máximo construyendo una red , donde${\displaystyle G=(X\cup Y,E)}$${\displaystyle G}$${\displaystyle N=(X\cup Y\cup \{s,t\},E')}$

1. ${\displaystyle E'}$contiene los bordes en dirección desde a .${\displaystyle G}$${\displaystyle X}$${\displaystyle Y}$
2. ${\displaystyle (s,x)\in E'}$para cada uno y para cada .${\displaystyle x\in X}$${\displaystyle (y,t)\in E'}$${\displaystyle y\in Y}$
3. ${\displaystyle c(e)=1}$para cada uno (ver figura 4.3.1).${\displaystyle e\in E'}$

Entonces, el valor del flujo máximo en es igual al tamaño de la coincidencia máxima en , y se puede encontrar una coincidencia de cardinalidad máxima tomando aquellos bordes que tienen flujo en un flujo máximo integral.${\displaystyle N}$${\displaystyle G}$${\displaystyle 1}$

Dado un grafo acíclico dirigido , debemos encontrar el número mínimo de caminos disjuntos en sus vértices para cubrir cada vértice en . Podemos construir un grafo bipartito a partir de , donde${\displaystyle G=(V,E)}$${\displaystyle V}$${\displaystyle G'=(V_{\textrm {out}}\cup V_{\textrm {in}},E')}$${\displaystyle G}$

1. ${\displaystyle V_{\textrm {out}}=\{v_{\textrm {out}}\mid v\in V\land v{\text{ has outgoing edge(s)}}\}}$
2. ${\displaystyle V_{\textrm {in}}=\{v_{\textrm {in}}\mid v\in V\land v{\text{ has incoming edge(s)}}\}}$
3. ${\displaystyle E'=\{(u_{\textrm {out}},v_{\textrm {in}})\in V_{out}\times V_{in}\mid (u,v)\in E\}}$.

Entonces se puede demostrar que tiene una coincidencia de tamaño si y solo si tiene una cubierta de caminos disjuntos en vértices que contiene aristas y caminos, donde es el número de vértices en . Por lo tanto, el problema se puede resolver encontrando la coincidencia de cardinalidad máxima en en su lugar.${\displaystyle G'}$${\displaystyle M}$${\displaystyle m}$${\displaystyle G}$${\displaystyle C}$${\displaystyle m}$${\displaystyle n-m}$${\displaystyle n}$${\displaystyle G}$${\displaystyle G'}$

Supongamos que hemos encontrado una coincidencia de , y hemos construido la cubierta a partir de ella. Intuitivamente, si dos vértices coinciden en , entonces la arista está contenida en . Claramente, el número de aristas en es . Para ver que es disjunto en cuanto a vértices, considere lo siguiente:${\displaystyle M}$${\displaystyle G'}$${\displaystyle C}$${\displaystyle u_{\mathrm {out} },v_{\mathrm {in} }}$${\displaystyle M}$${\displaystyle (u,v)}$${\displaystyle C}$${\displaystyle C}$${\displaystyle m}$${\displaystyle C}$

1. Cada vértice en puede no coincidir en , en cuyo caso no hay aristas que salgan en ; o puede coincidir en , en cuyo caso hay exactamente una arista que sale en . En cualquier caso, no más de una arista sale de ningún vértice en .${\displaystyle v_{\textrm {out}}}$${\displaystyle G'}$${\displaystyle M}$${\displaystyle v}$${\displaystyle C}$${\displaystyle v}$${\displaystyle C}$${\displaystyle v}$${\displaystyle C}$
2. De manera similar, para cada vértice en – si coincide, hay un único borde entrante en en ; de lo contrario, no tiene bordes entrantes en .${\displaystyle v_{\textrm {in}}}$${\displaystyle G'}$${\displaystyle v}$${\displaystyle C}$${\displaystyle v}$${\displaystyle C}$

Por lo tanto, ningún vértice tiene dos aristas entrantes o dos salientes en , lo que significa que todos los caminos en son disjuntos en sus vértices.${\displaystyle C}$${\displaystyle C}$

Para demostrar que la cubierta tiene un tamaño , comenzamos con una cubierta vacía y la construimos de forma incremental. Para agregar un vértice a la cubierta, podemos agregarlo a una ruta existente o crear una nueva ruta de longitud cero que comience en ese vértice. El primer caso es aplicable siempre que y alguna ruta en la cubierta comience en , o y alguna ruta termine en . El último caso es siempre aplicable. En el primer caso, el número total de aristas en la cubierta se incrementa en 1 y el número de rutas permanece igual; en el último caso, el número de rutas aumenta y el número de aristas permanece igual. Ahora está claro que después de cubrir todos los vértices, la suma del número de rutas y aristas en la cubierta es . Por lo tanto, si el número de aristas en la cubierta es , el número de rutas es .${\displaystyle C}$${\displaystyle n-m}$${\displaystyle u}$${\displaystyle (u,v)\in E}$${\displaystyle v}$${\displaystyle (v,u)\in E}$${\displaystyle v}$${\displaystyle n}$${\displaystyle n}$${\displaystyle m}$${\displaystyle n-m}$

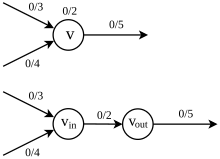
Sea una red. Supongamos que en cada nodo existe capacidad además de la capacidad de los bordes, es decir, una asignación tal que el flujo debe satisfacer no solo la restricción de capacidad y la conservación de flujos, sino también la restricción de capacidad de los vértices.${\displaystyle N=(V,E)}$${\displaystyle c:V\to \mathbb {R} ^{+},}$${\displaystyle f}$

${\displaystyle \sum _{i\in V}f_{iv}\leq c(v)\qquad \forall v\in V\backslash \{s,t\}.}$

En otras palabras, la cantidad de flujo que pasa a través de un vértice no puede exceder su capacidad. Para encontrar el flujo máximo a través de , podemos transformar el problema en el problema de flujo máximo en el sentido original expandiendo . Primero, cada uno se reemplaza por y , donde está conectado por aristas que entran y está conectado a aristas que salen de , luego asigna capacidad a la arista que conecta y (ver Fig. 4.4.1). En esta red expandida, se elimina la restricción de capacidad del vértice y, por lo tanto, el problema puede tratarse como el problema de flujo máximo original.${\displaystyle N}$${\displaystyle N}$${\displaystyle v\in V}$${\displaystyle v_{\text{in}}}$${\displaystyle v_{\text{out}}}$${\displaystyle v_{\text{in}}}$${\displaystyle v}$${\displaystyle v_{\text{out}}}$${\displaystyle v}$${\displaystyle c(v)}$${\displaystyle v_{\text{in}}}$${\displaystyle v_{\text{out}}}$

Dado un grafo dirigido y dos vértices y , debemos hallar el número máximo de caminos desde hasta . Este problema tiene varias variantes:${\displaystyle G=(V,E)}$${\displaystyle s}$${\displaystyle t}$${\displaystyle s}$${\displaystyle t}$

1. Los caminos deben estar separados por aristas. Este problema se puede transformar en un problema de flujo máximo construyendo una red a partir de , donde y son la fuente y el sumidero de respectivamente, y asignando a cada arista una capacidad de . En esta red, el flujo máximo es si y solo si hay caminos separados por aristas.${\displaystyle N=(V,E)}$${\displaystyle G}$${\displaystyle s}$${\displaystyle t}$${\displaystyle N}$${\displaystyle 1}$${\displaystyle k}$${\displaystyle k}$

2. Los caminos deben ser independientes, es decir, disjuntos en sus vértices (excepto y ). Podemos construir una red a partir de con capacidades de vértice, donde las capacidades de todos los vértices y todas las aristas son . Entonces el valor del flujo máximo es igual al número máximo de caminos independientes desde hasta .${\displaystyle s}$${\displaystyle t}$${\displaystyle N=(V,E)}$${\displaystyle G}$${\displaystyle 1}$${\displaystyle s}$${\displaystyle t}$

3. Además de que los caminos no tienen aristas unidas o vértices unidas, también tienen una restricción de longitud: contamos solo los caminos cuya longitud sea exactamente , o como máximo . La mayoría de las variantes de este problema son NP-completas, excepto para valores pequeños de . ^[27]${\displaystyle k}$${\displaystyle k}$${\displaystyle k}$

Un cierre de un grafo dirigido es un conjunto de vértices C , de modo que ninguna arista salga de C . El problema de cierre es la tarea de encontrar el cierre de peso máximo o peso mínimo en un grafo dirigido ponderado por vértices. Puede resolverse en tiempo polinómico utilizando una reducción al problema de flujo máximo.

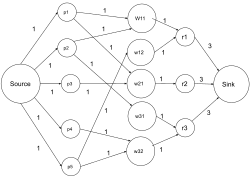
En el problema de eliminación del béisbol hay n equipos compitiendo en una liga. En una etapa específica de la temporada de la liga, w _i es el número de victorias y r _i es el número de juegos que quedan por jugar para el equipo i y r _ij es el número de juegos que quedan contra el equipo j . Un equipo es eliminado si no tiene ninguna posibilidad de terminar la temporada en primer lugar. La tarea del problema de eliminación del béisbol es determinar qué equipos son eliminados en cada punto durante la temporada. Schwartz ^[28] propuso un método que reduce este problema al flujo máximo de red. En este método se crea una red para determinar si el equipo k es eliminado.

Sea G = ( V , E ) una red con s , t ∈ V siendo la fuente y el sumidero respectivamente. Se agrega un nodo de juego _ij – que representa el número de jugadas entre estos dos equipos. También agregamos un nodo de equipo para cada equipo y conectamos cada nodo de juego { i , j } con i < j a V , y conectamos cada uno de ellos desde s por un borde con capacidad r _ij – que representa el número de jugadas entre estos dos equipos. También agregamos un nodo de equipo para cada equipo y conectamos cada nodo de juego { i , j } con dos nodos de equipo i y j para asegurar que uno de ellos gane. No es necesario restringir el valor del flujo en estos bordes. Finalmente, se crean bordes desde el nodo de equipo i hasta el nodo sumidero t y se establece la capacidad de w _k + r _k – w _i para evitar que el equipo i gane más de w _k + r _k . Sea S el conjunto de todos los equipos que participan en la liga y sea

${\displaystyle r(S-\{k\})=\sum _{i,j\in \{S-\{k\}\} \atop i<j}r_{ij}}$.

En este método se afirma que el equipo k no se elimina si y solo si existe un valor de flujo de tamaño r ( S − { k }) en la red G . En el artículo mencionado se demuestra que este valor de flujo es el valor de flujo máximo desde s hasta t .

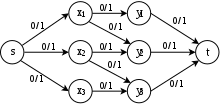
En la industria de las aerolíneas, un problema importante es la programación de las tripulaciones de vuelo. El problema de la programación de vuelos puede considerarse como una aplicación del flujo máximo de red extendido. La entrada de este problema es un conjunto de vuelos F que contiene la información sobre dónde y cuándo sale y llega cada vuelo. En una versión de la programación de vuelos, el objetivo es producir un programa factible con un máximo de k tripulaciones.

Para resolver este problema se utiliza una variación del problema de circulación llamada circulación limitada, que es la generalización de los problemas de flujo de red , con la restricción adicional de un límite inferior en los flujos de borde.

Sea G = ( V , E ) una red con s , t ∈ V como nodos de origen y destino. Para el origen y el destino de cada vuelo i , se suman dos nodos a V , el nodo s _i como origen y el nodo d _i como nodo de destino del vuelo i . También se suman las siguientes aristas a E :

1. Un borde con capacidad [0, 1] entre s y cada s _i .
2. Un borde con capacidad [0, 1] entre cada d _i y t .
3. Una arista con capacidad [1, 1] entre cada par de s _i y d _i .
4. Un borde con capacidad [0, 1] entre cada d _i y s _j , si la fuente s _j es alcanzable con una cantidad de tiempo y un costo razonables desde el destino del vuelo i .
5. Una arista con capacidad [0, ∞ ] entre s y t .

En el método mencionado, se afirma y demuestra que encontrar un valor de flujo de k en G entre s y t es igual a encontrar un programa factible para el conjunto de vuelos F con un máximo de k tripulaciones. ^[29]

Otra versión de la programación de aerolíneas es encontrar las tripulaciones mínimas necesarias para realizar todos los vuelos. Para encontrar una respuesta a este problema, se crea un grafo bipartito G' = ( A ∪ B , E ) donde cada vuelo tiene una copia en el conjunto A y el conjunto B . Si el mismo avión puede realizar el vuelo j después del vuelo i , i ∈ A está conectado a j ∈ B . Una coincidencia en G' induce un cronograma para F y obviamente la coincidencia bipartita máxima en este grafo produce un cronograma de aerolíneas con un número mínimo de tripulaciones. ^[29] Como se menciona en la parte de Aplicación de este artículo, la coincidencia bipartita de cardinalidad máxima es una aplicación del problema de flujo máximo.

Existen algunas fábricas que producen bienes y algunos pueblos a los que se deben entregar los bienes. Están conectados por una red de carreteras, cada una de las cuales tiene una capacidad c para el máximo de bienes que pueden circular por ella. El problema es encontrar si existe una circulación que satisfaga la demanda. Este problema se puede transformar en un problema de flujo máximo.

1. Agregue un nodo de origen s y agregue aristas desde él a cada nodo de fábrica f _i con capacidad p _i, donde p _i es la tasa de producción de la fábrica f _i .
2. Agregue un nodo sumidero t y agregue aristas de todas las aldeas v _i a t con capacidad d _i donde d _i es la tasa de demanda de la aldea v _i .

Sea G = ( V , E ) esta nueva red. Existe una circulación que satisface la demanda si y sólo si:

Valor máximo de caudal ( G ) .${\displaystyle =\sum _{i\in v}d_{i}}$

Si existe una circulación, mirar la solución de flujo máximo daría la respuesta de cuántas mercancías deben enviarse por una ruta particular para satisfacer las demandas.

El problema se puede ampliar añadiendo un límite inferior al flujo en algunos bordes. ^[30]

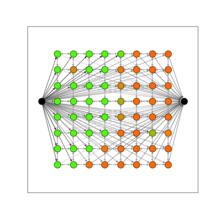
En su libro, Kleinberg y Tardos presentan un algoritmo para segmentar una imagen. ^[32] Presentan un algoritmo para encontrar el fondo y el primer plano en una imagen. Más precisamente, el algoritmo toma un mapa de bits como entrada modelado de la siguiente manera: a _i ≥ 0 es la probabilidad de que el píxel i pertenezca al primer plano, b _i ≥ 0 en la probabilidad de que el píxel i pertenezca al fondo, y p _ij es la penalización si dos píxeles adyacentes i y j se colocan uno en el primer plano y el otro en el fondo. El objetivo es encontrar una partición ( A , B ) del conjunto de píxeles que maximice la siguiente cantidad

${\displaystyle q(A,B)=\sum _{i\in A}a_{i}+\sum _{i\in B}b_{i}-\sum _{\begin{matrix}i,j{\text{ adjacent}}\\|A\cap \{i,j\}|=1\end{matrix}}p_{ij}}$,

En efecto, para los píxeles de A (considerados como primer plano), ganamos a _i ; para todos los píxeles de B (considerados como el fondo), ganamos b _i . En el borde, entre dos píxeles adyacentes i y j , perdemos p _ij . Es equivalente a minimizar la cantidad

${\displaystyle q'(A,B)=\sum _{i\in A}b_{i}+\sum _{i\in B}a_{i}+\sum _{\begin{matrix}i,j{\text{ adjacent}}\\|A\cap \{i,j\}|=1\end{matrix}}p_{ij}}$

porque

${\displaystyle q(A,B)=\sum _{i\in A\cup B}a_{i}+\sum _{i\in A\cup B}b_{i}-q'(A,B).}$

Ahora construimos la red cuyos nodos son el píxel, más una fuente y un sumidero, ver Figura a la derecha. Conectamos la fuente al píxel i mediante un borde de peso a _i . Conectamos el píxel i al sumidero mediante un borde de peso b _i . Conectamos el píxel i al píxel j con peso p _ij . Ahora, queda calcular un corte mínimo en esa red (o equivalentemente un flujo máximo). La última figura muestra un corte mínimo.

_1. En el problema de flujo de costo mínimo , cada arista ( u _, v) también tiene un coeficiente _de costo auv además de su capacidad. Si el flujo a través de la arista es fuv , entonces el costo total es auv _fuv . Se requiere encontrar un flujo de un tamaño dado d , con el menor costo. En la mayoría de las variantes, los coeficientes de costo pueden ser positivos o negativos. Existen varios algoritmos de tiempo polinomial para este problema.

2. El problema del flujo máximo puede ampliarse con restricciones disyuntivas : una restricción disyuntiva negativa dice que un cierto par de aristas no puede tener simultáneamente un flujo distinto de cero; una restricción disyuntiva positiva dice que, en un cierto par de aristas, al menos una debe tener un flujo distinto de cero. Con restricciones negativas, el problema se vuelve fuertemente NP-difícil incluso para redes simples. Con restricciones positivas, el problema es polinomial si se permiten flujos fraccionarios, pero puede ser fuertemente NP-difícil cuando los flujos deben ser integrales. ^[33]

• Joseph Cheriyan y Kurt Mehlhorn (1999). "Análisis de la regla de selección de nivel más alto en el algoritmo de flujo máximo de preflujo-empuje". Information Processing Letters . 69 (5): 239–242. CiteSeerX  10.1.1.42.8563 . doi :10.1016/S0020-0190(99)00019-8.
• Daniel D. Sleator y Robert E. Tarjan (1983). "Una estructura de datos para árboles dinámicos" (PDF) . Revista de Ciencias de la Computación y de Sistemas . 26 (3): 362–391. doi :10.1016/0022-0000(83)90006-5. ISSN  0022-0000.
• Eugene Lawler (2001). "4. Flujos de red". Optimización combinatoria: redes y matroides . Dover. págs. 109-177. ISBN 978-0-486-41453-9.