Flujo óptico

El flujo óptico o flujo óptico es el patrón de movimiento aparente de objetos, superficies y bordes en una escena visual causado por el movimiento relativo entre un observador y una escena. ^{[1] [2]} El flujo óptico también se puede definir como la distribución de velocidades aparentes de movimiento del patrón de brillo en una imagen. ^[3]

El concepto de flujo óptico fue introducido por el psicólogo estadounidense James J. Gibson en la década de 1940 para describir el estímulo visual proporcionado a los animales que se mueven por el mundo. ^[4] Gibson destacó la importancia del flujo óptico para la percepción de posibilidades de acción dentro del entorno. Los seguidores de Gibson y su enfoque ecológico de la psicología han demostrado además el papel del estímulo del flujo óptico para la percepción del movimiento por parte del observador en el mundo; la percepción de la forma, la distancia y el movimiento de los objetos en el mundo; y el control de la locomoción . ^[5]

El término flujo óptico también es utilizado por los expertos en robótica, abarcando técnicas relacionadas con el procesamiento de imágenes y el control de la navegación, incluyendo la detección de movimiento , la segmentación de objetos , la información de tiempo de contacto, los cálculos de enfoque de expansión, la luminancia, la codificación con compensación de movimiento y la medición de disparidad estéreo. ^{[6] [7]}

Las secuencias de imágenes ordenadas permiten estimar el movimiento como velocidades de imagen instantáneas o desplazamientos de imagen discretos. ^[7] Fleet y Weiss ofrecen una introducción didáctica al flujo óptico basado en gradientes. ^[8] John L. Barron, David J. Fleet y Steven Beauchemin ofrecen un análisis del rendimiento de una serie de técnicas de flujo óptico. Se hace hincapié en la precisión y la densidad de las mediciones. ^[9]

Los métodos de flujo óptico intentan calcular el movimiento entre dos fotogramas de imágenes que se toman en momentos y en cada posición de vóxel . Estos métodos se denominan diferenciales porque se basan en aproximaciones locales de la serie de Taylor de la señal de la imagen; es decir, utilizan derivadas parciales con respecto a las coordenadas espaciales y temporales.${\displaystyle t}$${\displaystyle t+\Delta t}$

Para un caso (2D +  t )-dimensional (los casos 3D o n -D son similares), un vóxel en una ubicación con intensidad se habrá movido , y entre los dos cuadros de imagen, y se puede dar la siguiente restricción de constancia de brillo : ${\displaystyle (x,y,t)}$${\displaystyle I(x,y,t)}$${\displaystyle \Delta x}$${\displaystyle \Delta y}$${\displaystyle \Delta t}$

${\displaystyle I(x,y,t)=I(x+\Delta x,y+\Delta y,t+\Delta t)}$

Suponiendo que el movimiento es pequeño, la restricción de imagen con series de Taylor se puede desarrollar para obtener:${\displaystyle I(x,y,t)}$

${\displaystyle I(x+\Delta x,y+\Delta y,t+\Delta t)=I(x,y,t)+{\frac {\partial I}{\partial x}}\,\Delta x+{\frac {\partial I}{\partial y}}\,\Delta y+{\frac {\partial I}{\partial t}}\,\Delta t+{}}$términos de orden superior

Al truncar los términos de orden superior (lo que realiza una linealización) se deduce que:

${\displaystyle {\frac {\partial I}{\partial x}}\Delta x+{\frac {\partial I}{\partial y}}\Delta y+{\frac {\partial I}{\partial t}}\Delta t=0}$

o, dividiendo por ,${\displaystyle \Delta t}$

${\displaystyle {\frac {\partial I}{\partial x}}{\frac {\Delta x}{\Delta t}}+{\frac {\partial I}{\partial y}}{\frac {\Delta y}{\Delta t}}+{\frac {\partial I}{\partial t}}{\frac {\Delta t}{\Delta t}}=0}$

Lo que resulta en

${\displaystyle {\frac {\partial I}{\partial x}}V_{x}+{\frac {\partial I}{\partial y}}V_{y}+{\frac {\partial I}{\partial t}}=0}$

donde son los componentes y de la velocidad o flujo óptico de y , y son las derivadas de la imagen en en las direcciones correspondientes. , y se pueden escribir para las derivadas en lo siguiente.${\displaystyle V_{x},V_{y}}$${\displaystyle x}$${\displaystyle y}$${\displaystyle I(x,y,t)}$${\displaystyle {\tfrac {\partial I}{\partial x}}}$${\displaystyle {\tfrac {\partial I}{\partial y}}}$${\displaystyle {\tfrac {\partial I}{\partial t}}}$${\displaystyle (x,y,t)}$${\displaystyle I_{x}}$${\displaystyle I_{y}}$${\displaystyle I_{t}}$

De este modo:

${\displaystyle I_{x}V_{x}+I_{y}V_{y}=-I_{t}}$

o

${\displaystyle \nabla I\cdot {\vec {V}}=-I_{t}}$

Se trata de una ecuación con dos incógnitas y no se puede resolver como tal. Se la conoce como el problema de apertura de los algoritmos de flujo óptico. Para encontrar el flujo óptico se necesita otro conjunto de ecuaciones, determinado por alguna restricción adicional. Todos los métodos de flujo óptico introducen condiciones adicionales para estimar el flujo real.

• Correlación de fase : inversa del espectro de potencia cruzada normalizado
• Métodos basados ​​en bloques: minimización de la suma de las diferencias al cuadrado o la suma de las diferencias absolutas , o maximización de la correlación cruzada normalizada
• Métodos diferenciales de estimación del flujo óptico, basados ​​en derivadas parciales de la señal de imagen y/o del campo de flujo buscado y derivadas parciales de orden superior, tales como:
  • Método de Lucas-Kanade : sobre parches de imagen y un modelo afín para el campo de flujo ^[10]
  • Método de Horn-Schunck : optimización de un funcional basado en residuos de la restricción de constancia de brillo y un término de regularización particular que expresa la suavidad esperada del campo de flujo ^[10]
  • Método Buxton-Buxton, basado en un modelo del movimiento de los bordes en secuencias de imágenes ^[11]
  • Método de Black-Jepson: flujo óptico grueso mediante correlación ^[7]
  • Métodos variacionales generales : una gama de modificaciones/extensiones de Horn–Schunck, utilizando otros términos de datos y otros términos de suavidad.
• Métodos de optimización discreta: se cuantifica el espacio de búsqueda y luego se aborda la coincidencia de imágenes mediante la asignación de etiquetas en cada píxel, de modo que la deformación correspondiente minimice la distancia entre la imagen de origen y la de destino. ^[12] La solución óptima a menudo se recupera mediante algoritmos de teorema de corte mínimo de flujo máximo , programación lineal o métodos de propagación de creencias .

Muchos de estos, además de los algoritmos de última generación actuales, se evalúan en el conjunto de datos de referencia de Middlebury. ^{[13] [14]} Otros conjuntos de datos de referencia populares son KITTI y Sintel .

La estimación del movimiento y la compresión de vídeo se han convertido en un aspecto importante de la investigación del flujo óptico. Si bien el campo de flujo óptico es superficialmente similar a un campo de movimiento denso derivado de las técnicas de estimación de movimiento, el flujo óptico es el estudio no solo de la determinación del campo de flujo óptico en sí, sino también de su uso para estimar la naturaleza y la estructura tridimensionales de la escena, así como el movimiento 3D de los objetos y del observador en relación con la escena, la mayoría de ellos utilizando el jacobiano de imagen. ^[15]

Los investigadores en robótica han utilizado el flujo óptico en muchas áreas, como detección y seguimiento de objetos, extracción del plano dominante de la imagen, detección de movimiento, navegación robótica y odometría visual . ^[6] La información del flujo óptico ha sido reconocida como útil para controlar microvehículos aéreos. ^[16]

La aplicación del flujo óptico incluye el problema de inferir no sólo el movimiento del observador y de los objetos en la escena, sino también la estructura de los objetos y del entorno. Dado que la conciencia del movimiento y la generación de mapas mentales de la estructura de nuestro entorno son componentes críticos de la visión animal (y humana) , la conversión de esta capacidad innata en una capacidad informática es igualmente crucial en el campo de la visión artificial . ^[17]

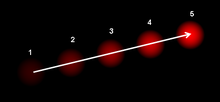
Consideremos un clip de cinco fotogramas de una pelota que se mueve desde la parte inferior izquierda de un campo de visión hasta la parte superior derecha. Las técnicas de estimación de movimiento pueden determinar que en un plano bidimensional la pelota se mueve hacia arriba y hacia la derecha y los vectores que describen este movimiento se pueden extraer de la secuencia de fotogramas. Para los fines de la compresión de vídeo (por ejemplo, MPEG ), la secuencia ahora se describe tan bien como debe ser. Sin embargo, en el campo de la visión artificial, la cuestión de si la pelota se mueve hacia la derecha o si el observador se mueve hacia la izquierda es una información incognoscible pero crítica. Ni siquiera si hubiera un fondo estático y con patrones en los cinco fotogramas, podríamos afirmar con seguridad que la pelota se mueve hacia la derecha, porque el patrón podría tener una distancia infinita hasta el observador.

Existen varias configuraciones de sensores de flujo óptico. Una configuración es un chip sensor de imagen conectado a un procesador programado para ejecutar un algoritmo de flujo óptico. Otra configuración utiliza un chip de visión, que es un circuito integrado que tiene tanto el sensor de imagen como el procesador en el mismo chip, lo que permite una implementación compacta. ^{[18] [19]} Un ejemplo de esto es un sensor de ratón óptico genérico utilizado en un ratón óptico . En algunos casos, el circuito de procesamiento se puede implementar utilizando circuitos analógicos o de señal mixta para permitir un cálculo rápido del flujo óptico utilizando un consumo de corriente mínimo.

Un área de investigación contemporánea es el uso de técnicas de ingeniería neuromórfica para implementar circuitos que responden al flujo óptico y, por lo tanto, pueden ser apropiados para su uso en un sensor de flujo óptico. ^[20] Dichos circuitos pueden inspirarse en circuitos neuronales biológicos que responden de manera similar al flujo óptico.

Los sensores de flujo óptico se utilizan ampliamente en los ratones ópticos de computadora , como el principal componente de detección para medir el movimiento del ratón a través de una superficie.

Los sensores de flujo óptico también se utilizan en aplicaciones robóticas , principalmente cuando es necesario medir el movimiento visual o el movimiento relativo entre el robot y otros objetos en las proximidades del robot. El uso de sensores de flujo óptico en vehículos aéreos no tripulados (UAV) , para estabilidad y evitación de obstáculos, también es un área de investigación actual. ^[21]

• Matriz óptica ambiental
• Ratón óptico
• Imágenes de alcance
• Unidad de procesamiento de visión
• Ecuación de continuidad
• Campo de movimiento

Wikimedia Commons alberga una categoría multimedia sobre Flujo óptico .

• Encontrar el flujo óptico
• Artículo sobre el arte del flujo óptico en fxguide.com (utilizando el flujo óptico en efectos visuales)
• Evaluación de flujo óptico y secuencias de verdad fundamental.
• Evaluación del flujo óptico de Middlebury y secuencias de verdad fundamental.
• mrf-registration.net - Estimación del flujo óptico mediante MRF
• Laboratorio Aeroespacial Francés: Implementación en GPU de un flujo óptico basado en Lucas-Kanade
• Implementación de CUDA por CUVI (CUDA Vision & Imaging Library)
• Flujo óptico de Horn y Schunck: demostración en línea y código fuente del método de Horn y Schunck
• Flujo óptico TV-L1: demostración en línea y código fuente del método de Zach et al.
• Flujo óptico robusto: demostración en línea y código fuente del método de Brox et al.