Teoría de vigas de Euler-Bernoulli

La teoría de vigas de Euler-Bernoulli (también conocida como teoría de vigas de ingeniero o teoría clásica de vigas ) [1] es una simplificación de la teoría lineal de elasticidad que proporciona un medio para calcular las características de carga y deflexión de las vigas . Cubre el caso correspondiente a pequeñas deflexiones de una viga que está sujeta solo a cargas laterales. Al ignorar los efectos de la deformación cortante y la inercia rotatoria, es un caso especial de la teoría de vigas de Timoshenko-Ehrenfest . Se enunció por primera vez alrededor de 1750, [2] pero no se aplicó a gran escala hasta el desarrollo de la Torre Eiffel y la noria a fines del siglo XIX. Después de estas demostraciones exitosas, rápidamente se convirtió en una piedra angular de la ingeniería y un facilitador de la Segunda Revolución Industrial .
Se han desarrollado modelos matemáticos adicionales , como la teoría de placas , pero la simplicidad de la teoría de vigas la convierte en una herramienta importante en las ciencias, especialmente en la ingeniería estructural y mecánica .
Historia

El consenso predominante es que Galileo Galilei hizo los primeros intentos de desarrollar una teoría de vigas, pero estudios recientes sostienen que Leonardo da Vinci fue el primero en hacer las observaciones cruciales. Da Vinci carecía de la ley de Hooke y del cálculo para completar la teoría, mientras que Galileo se vio frenado por una suposición incorrecta que hizo. [3]
La viga de Bernoulli recibe su nombre de Jacob Bernoulli , quien realizó importantes descubrimientos. Leonhard Euler y Daniel Bernoulli fueron los primeros en desarrollar una teoría útil alrededor de 1750. [4]
Ecuación de viga estática
La ecuación de Euler-Bernoulli describe la relación entre la desviación de la viga y la carga aplicada: [5]
La curva describe la desviación de la viga en la dirección en alguna posición (recuerde que la viga se modela como un objeto unidimensional). es una carga distribuida, en otras palabras, una fuerza por unidad de longitud (análoga a la presión que es una fuerza por área); puede ser una función de , u otras variables. es el módulo elástico y es el segundo momento del área de la sección transversal de la viga. debe calcularse con respecto al eje que es perpendicular a la carga aplicada. [N 1] Explícitamente, para una viga cuyo eje está orientado a lo largo de una carga a lo largo de , la sección transversal de la viga está en el plano y el segundo momento del área relevante es
donde se supone que el centroide de la sección transversal se encuentra en .
A menudo, el producto (conocido como rigidez a la flexión ) es una constante, de modo que
Esta ecuación, que describe la deflexión de una viga estática uniforme, se utiliza ampliamente en la práctica de la ingeniería. Las expresiones tabuladas para la deflexión para configuraciones de vigas comunes se pueden encontrar en manuales de ingeniería. Para situaciones más complicadas, la deflexión se puede determinar resolviendo la ecuación de Euler-Bernoulli utilizando técnicas como " integración directa ", " método de Macaulay ", " método del área de momento " , " método de viga conjugada ", " principio del trabajo virtual ", " método de Castigliano ", " método de flexibilidad ", " método de deflexión de pendiente ", " método de distribución de momentos " o " método de rigidez directa ".
Aquí se definen las convenciones de signos, ya que se pueden encontrar diferentes convenciones en la literatura. [5] En este artículo, se utiliza un sistema de coordenadas diestro con el eje a la derecha, el eje apuntando hacia arriba y el eje apuntando hacia la figura. El signo del momento flector se toma como positivo cuando el vector de torsión asociado con el momento flector en el lado derecho de la sección está en la dirección positiva, es decir, un valor positivo de produce tensión de compresión en la superficie inferior. Con esta elección de la convención de signos del momento flector, para tener , es necesario que la fuerza cortante que actúa en el lado derecho de la sección sea positiva en la dirección para lograr el equilibrio estático de momentos. Si la intensidad de carga se toma positiva en la dirección positiva, entonces es necesario para el equilibrio de fuerzas.
Las derivadas sucesivas de la desviación tienen significados físicos importantes: es la pendiente de la viga, que es el ángulo de rotación en sentido antihorario alrededor del eje en el límite de pequeños desplazamientos;
es el momento flector en la viga; y
es la fuerza cortante en la viga.
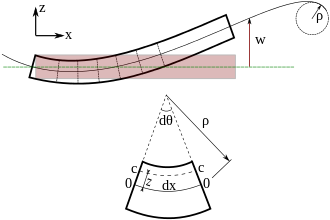
Las tensiones en una viga se pueden calcular a partir de las expresiones anteriores después de determinar la desviación debida a una carga dada.
Derivación de la ecuación de flexión
Debido a la importancia fundamental de la ecuación del momento flector en ingeniería, proporcionaremos una breve derivación. Pasamos a coordenadas polares. La longitud del eje neutro en la figura es La longitud de una fibra con una distancia radial por debajo del eje neutro es Por lo tanto, la deformación de esta fibra es
La tensión de esta fibra es donde es el módulo elástico de acuerdo con la Ley de Hooke . El vector de fuerza diferencial, resultante de esta tensión, viene dado por
Este es el vector de fuerza diferencial ejercido en el lado derecho de la sección que se muestra en la figura. Sabemos que está en la dirección ya que la figura muestra claramente que las fibras en la mitad inferior están en tensión. es el elemento diferencial de área en la ubicación de la fibra. El vector de momento flector diferencial, asociado con, está dado por
Esta expresión es válida para las fibras de la mitad inferior de la viga. La expresión para las fibras de la mitad superior de la viga será similar, excepto que el vector del brazo de momento estará en la dirección positiva y el vector de fuerza estará en la dirección ya que las fibras superiores están en compresión. Pero el vector de momento flector resultante seguirá estando en la dirección ya que Por lo tanto, integramos sobre toda la sección transversal de la viga y obtenemos para el vector de momento flector ejercido sobre la sección transversal derecha de la viga la expresión
donde es el segundo momento del área . A partir del cálculo, sabemos que cuando es pequeño, como lo es para una viga de Euler-Bernoulli, podemos hacer la aproximación , donde es el radio de curvatura . Por lo tanto,
Esta ecuación vectorial se puede separar en la definición del vector unitario de flexión ( está orientada como ), y en la ecuación de flexión:
Ecuación de viga dinámica

La ecuación de la viga dinámica es la ecuación de Euler-Lagrange para la siguiente acción
El primer término representa la energía cinética, donde es la masa por unidad de longitud, el segundo término representa la energía potencial debida a las fuerzas internas (cuando se considera con un signo negativo) y el tercer término representa la energía potencial debida a la carga externa . La ecuación de Euler-Lagrange se utiliza para determinar la función que minimiza la funcional . Para una viga dinámica de Euler-Bernoulli, la ecuación de Euler-Lagrange es
| Derivación de la ecuación de Euler-Lagrange para vigas |
|---|
| Dado que el Lagrangiano es La ecuación de Euler-Lagrange correspondiente es Ahora, Al introducirlo en la ecuación de Euler-Lagrange se obtiene o, que es la ecuación que gobierna la dinámica de una viga de Euler-Bernoulli. |
Cuando la viga es homogénea, y son independientes de , y la ecuación de la viga es más simple:
Vibración libre
En ausencia de una carga transversal, , tenemos la ecuación de vibración libre . Esta ecuación se puede resolver utilizando una descomposición de Fourier del desplazamiento en la suma de vibraciones armónicas de la forma
donde es la frecuencia de vibración. Entonces, para cada valor de frecuencia, podemos resolver una ecuación diferencial ordinaria
La solución general de la ecuación anterior es
donde son constantes. Estas constantes son únicas para un conjunto dado de condiciones de contorno. Sin embargo, la solución para el desplazamiento no es única y depende de la frecuencia. Estas soluciones se escriben típicamente como
Las cantidades se denominan frecuencias naturales del haz. Cada una de las soluciones de desplazamiento se denomina modo y la forma de la curva de desplazamiento se denomina forma de modo .
Ejemplo: Viga en voladizo

Las condiciones de contorno para una viga en voladizo de longitud (fijada en ) son
Si aplicamos estas condiciones, se encuentra que existen soluciones no triviales solo si Esta ecuación no lineal se puede resolver numéricamente. Las primeras cuatro raíces son , , y .
Las frecuencias naturales de vibración correspondientes son
Las condiciones de contorno también se pueden utilizar para determinar las formas modales a partir de la solución para el desplazamiento:

La constante desconocida (en realidad constantes ya que hay una para cada ) , que en general es compleja, está determinada por las condiciones iniciales en la velocidad y los desplazamientos de la viga. Normalmente se utiliza un valor de al trazar formas modales. Las soluciones al problema forzado no amortiguado tienen desplazamientos ilimitados cuando la frecuencia de excitación coincide con una frecuencia natural , es decir, la viga puede resonar . Por lo tanto, las frecuencias naturales de una viga corresponden a las frecuencias en las que puede producirse resonancia .
Ejemplo: viga libre-libre (sin soporte)

Una viga libre-libre es una viga sin ningún soporte. [6] Las condiciones de contorno para una viga libre-libre de longitud que se extiende de a están dadas por:
Si aplicamos estas condiciones, se descubre que existen soluciones no triviales sólo si
Esta ecuación no lineal se puede resolver numéricamente. Las primeras cuatro raíces son , , , y .
Las frecuencias naturales de vibración correspondientes son:
Las condiciones de contorno también se pueden utilizar para determinar las formas modales a partir de la solución para el desplazamiento:
Al igual que con la viga en voladizo, las constantes desconocidas están determinadas por las condiciones iniciales en la velocidad y los desplazamientos de la viga. Además, las soluciones al problema forzado no amortiguado tienen desplazamientos ilimitados cuando la frecuencia de excitación coincide con una frecuencia natural .
Ejemplo: viga sujetada-sujetada
Las condiciones de contorno de una viga doblemente sujeta [7] de longitud (fijada en y ) son
Esto implica que existen soluciones para la configuración que impone esta condición. La reorganización para la frecuencia natural da
Estrés
Además de la deflexión, la ecuación de vigas describe fuerzas y momentos y, por lo tanto, se puede utilizar para describir tensiones . Por este motivo, la ecuación de vigas de Euler-Bernoulli se utiliza ampliamente en ingeniería , especialmente civil y mecánica, para determinar la resistencia (así como la deflexión) de las vigas bajo flexión.
Tanto el momento flector como la fuerza cortante provocan tensiones en la viga. La tensión debida a la fuerza cortante es máxima a lo largo del eje neutro de la viga (cuando el ancho de la viga, t, es constante a lo largo de la sección transversal de la viga; de lo contrario, se debe evaluar una integral que involucre el primer momento y el ancho de la viga para la sección transversal particular), y la tensión de tracción máxima se encuentra en las superficies superior o inferior. Por lo tanto, la tensión principal máxima en la viga puede no estar ni en la superficie ni en el centro, sino en un área general. Sin embargo, las tensiones de fuerza cortante son insignificantes en comparación con las tensiones de momento flector en todas las vigas, excepto en las más robustas, así como el hecho de que las concentraciones de tensión ocurren comúnmente en las superficies, lo que significa que es probable que la tensión máxima en una viga esté en la superficie.
Curvado simple o simétrico

Para secciones transversales de vigas que son simétricas respecto de un plano perpendicular al plano neutro, se puede demostrar que la tensión de tracción experimentada por la viga se puede expresar como:
Aquí, es la distancia desde el eje neutro hasta un punto de interés; y es el momento de flexión. Nótese que esta ecuación implica que la flexión pura (de signo positivo) causará tensión cero en el eje neutro, tensión positiva (de tracción) en la "parte superior" de la viga y tensión negativa (de compresión) en la parte inferior de la viga; y también implica que la tensión máxima estará en la superficie superior y la mínima en la parte inferior. Esta tensión de flexión puede superponerse con tensiones aplicadas axialmente, lo que causará un desplazamiento en el eje neutro (tensión cero).
Tensiones máximas en una sección transversal

La tensión máxima de tracción en una sección transversal está en la posición y la tensión máxima de compresión está en la posición donde la altura de la sección transversal es . Estas tensiones son
Las cantidades son los módulos de sección [5] y se definen como
El módulo de sección combina toda la información geométrica importante sobre la sección de una viga en una sola cantidad. Para el caso en que una viga es doblemente simétrica, tenemos un módulo de sección .
Deformación en una viga de Euler-Bernoulli
Necesitamos una expresión para la deformación en términos de la deflexión de la superficie neutra para relacionar las tensiones en una viga de Euler-Bernoulli con la deflexión. Para obtener esa expresión, utilizamos la suposición de que las normales a la superficie neutra permanecen normales durante la deformación y que las deflexiones son pequeñas. Estas suposiciones implican que la viga se dobla en un arco de círculo de radio (ver Figura 1) y que la superficie neutra no cambia de longitud durante la deformación. [5]
Sea la longitud de un elemento de la superficie neutra en estado no deformado. Para desviaciones pequeñas, el elemento no cambia su longitud después de doblarse, sino que se deforma en un arco de círculo de radio . Si es el ángulo subtendido por este arco, entonces .
Consideremos ahora otro segmento del elemento a una distancia por encima de la superficie neutra. La longitud inicial de este elemento es . Sin embargo, después de doblarlo, la longitud del elemento se convierte en . La deformación en ese segmento de la viga está dada por
donde es la curvatura de la viga. Esto nos da la deformación axial en la viga como función de la distancia desde la superficie neutra. Sin embargo, todavía necesitamos encontrar una relación entre el radio de curvatura y la deflexión de la viga .
Relación entre la curvatura y la deflexión del haz
Sea P un punto de la superficie neutra de la viga a una distancia del origen del sistema de coordenadas. La pendiente de la viga es aproximadamente igual al ángulo que forma la superficie neutra con el eje para los ángulos pequeños que se encuentran en la teoría de vigas. Por lo tanto, con esta aproximación,
Por lo tanto, para un elemento infinitesimal , la relación se puede escribir como
Por lo tanto, la deformación en la viga puede expresarse como
Relaciones tensión-deformación
Para un material elástico lineal isótropo homogéneo , la tensión está relacionada con la deformación mediante , donde es el módulo de Young . Por lo tanto, la tensión en una viga de Euler-Bernoulli está dada por
Obsérvese que la relación anterior, cuando se compara con la relación entre la tensión axial y el momento flector, conduce a
Dado que la fuerza cortante está dada por , también tenemos
Consideraciones sobre límites
La ecuación de la viga contiene una derivada de cuarto orden en . Para encontrar una solución única necesitamos cuatro condiciones de contorno. Las condiciones de contorno normalmente modelan apoyos , pero también pueden modelar cargas puntuales, cargas distribuidas y momentos. Las condiciones de contorno de apoyo o desplazamiento se utilizan para fijar valores de desplazamiento ( ) y rotaciones ( ) en el contorno. Dichas condiciones de contorno también se denominan condiciones de contorno de Dirichlet . Las condiciones de contorno de carga y momento implican derivadas más altas de y representan el flujo de momento . Las condiciones de contorno de flujo también se denominan condiciones de contorno de Neumann .
Como ejemplo, considere una viga en voladizo que está incorporada en un extremo y libre en el otro, como se muestra en la figura adyacente. En el extremo incorporado de la viga no puede haber ningún desplazamiento o rotación de la viga. Esto significa que en el extremo izquierdo tanto la deflexión como la pendiente son cero. Dado que no se aplica ningún momento de flexión externo en el extremo libre de la viga, el momento de flexión en esa ubicación es cero. Además, si no se aplica ninguna fuerza externa a la viga, la fuerza de corte en el extremo libre también es cero.
Tomando la coordenada del extremo izquierdo como y la del extremo derecho como (la longitud de la viga), estas afirmaciones se traducen al siguiente conjunto de condiciones de contorno (supongamos que es una constante):

Un soporte simple (pasador o rodillo) es equivalente a una fuerza puntual sobre la viga que se ajusta de tal manera que fija la posición de la viga en ese punto. Un soporte fijo o abrazadera, es equivalente a la combinación de una fuerza puntual y un torque puntual que se ajusta de tal manera que fija tanto la posición como la pendiente de la viga en ese punto. Las fuerzas y torques puntuales, ya sea de soportes o aplicados directamente, dividirán una viga en un conjunto de segmentos, entre los cuales la ecuación de la viga producirá una solución continua, dadas cuatro condiciones de contorno, dos en cada extremo del segmento. Suponiendo que el producto EI es una constante, y definiendo donde F es la magnitud de una fuerza puntual, y donde M es la magnitud de un torque puntual, las condiciones de contorno apropiadas para algunos casos comunes se dan en la tabla a continuación. El cambio en una derivada particular de w a través del límite a medida que x aumenta se denota por seguido de esa derivada. Por ejemplo, donde es el valor de en el límite inferior del segmento superior, mientras que es el valor de en el límite superior del segmento inferior. Cuando los valores de la derivada particular no sólo son continuos a través del límite, sino también fijos, la condición de límite se escribe eg, que en realidad constituye dos ecuaciones separadas (eg, = fijo).
Límite Abrazadera Soporte simple Fuerza puntual Punto de torsión Extremo libre Abrazadera en el extremo fijado fijado Extremo simplemente apoyado fijado Fuerza puntual al final Punto de torsión al final
Obsérvese que en los primeros casos, en los que las fuerzas y los pares puntuales se encuentran entre dos segmentos, existen cuatro condiciones de contorno, dos para el segmento inferior y dos para el superior. Cuando se aplican fuerzas y pares a un extremo de la viga, se dan dos condiciones de contorno que se aplican en ese extremo. El signo de las fuerzas y los pares puntuales en un extremo será positivo para el extremo inferior y negativo para el extremo superior.
Consideraciones sobre la carga
Las cargas aplicadas pueden representarse mediante condiciones de contorno o mediante la función que representa una carga distribuida externa. El uso de cargas distribuidas suele ser favorable para la simplicidad. Sin embargo, las condiciones de contorno se utilizan a menudo para modelar cargas según el contexto; esta práctica es especialmente común en el análisis de vibraciones.
Por naturaleza, la carga distribuida se representa muy a menudo de manera fragmentaria, ya que en la práctica una carga no suele ser una función continua. Las cargas puntuales se pueden modelar con la ayuda de la función delta de Dirac . Por ejemplo, considere una viga voladiza estática uniforme de longitud con una carga puntual ascendente aplicada en el extremo libre. Usando condiciones de contorno, esto se puede modelar de dos maneras. En el primer enfoque, la carga puntual aplicada se aproxima mediante una fuerza de corte aplicada en el extremo libre. En ese caso, la ecuación gobernante y las condiciones de contorno son:
Alternativamente, podemos representar la carga puntual como una distribución utilizando la función de Dirac. En ese caso, la ecuación y las condiciones de contorno son
Nótese que se elimina la condición de contorno de fuerza de corte (tercera derivada), de lo contrario habría una contradicción. Estos son problemas de valor de contorno equivalentes y ambos arrojan la solución
La aplicación de varias cargas puntuales en diferentes ubicaciones dará lugar a una función por partes. El uso de la función de Dirac simplifica enormemente estas situaciones; de lo contrario, la viga tendría que dividirse en secciones, cada una con cuatro condiciones de contorno resueltas por separado. Una familia bien organizada de funciones denominadas funciones de singularidad se utilizan a menudo como una abreviatura de la función de Dirac, su derivada y sus antiderivadas .
Los fenómenos dinámicos también se pueden modelar utilizando la ecuación estática de la viga, eligiendo formas adecuadas de distribución de carga. Por ejemplo, la vibración libre de una viga se puede tener en cuenta utilizando la función de carga:
donde es la densidad de masa lineal de la viga, no necesariamente constante. Con esta carga dependiente del tiempo, la ecuación de la viga será una ecuación diferencial parcial :
Otro ejemplo interesante describe la desviación de una viga que gira con una frecuencia angular constante de :
Esta es una distribución de fuerza centrípeta . Nótese que en este caso, es una función del desplazamiento (la variable dependiente), y la ecuación de la viga será una ecuación diferencial ordinaria autónoma .
Ejemplos
Flexión de tres puntos
El ensayo de flexión en tres puntos es un experimento clásico en mecánica. Representa el caso de una viga apoyada sobre dos apoyos de rodillos y sometida a una carga concentrada aplicada en el centro de la viga. El esfuerzo cortante es constante en valor absoluto: es la mitad de la carga central, P/2. Cambia de signo en el centro de la viga. El momento flector varía linealmente desde un extremo, donde es 0, y el centro donde su valor absoluto es PL/4, es donde el riesgo de ruptura es más importante. La deformación de la viga se describe mediante un polinomio de tercer grado sobre una media viga (siendo la otra mitad simétrica). Los momentos flectores ( ), las fuerzas cortantes ( ) y las deflexiones ( ) para una viga sometida a una carga puntual central y una carga puntual asimétrica se dan en la siguiente tabla. [5]
| Distribución | Valor máximo | |
|---|---|---|
| Viga simplemente apoyada con carga central |  | |
| Viga simplemente apoyada con carga asimétrica | 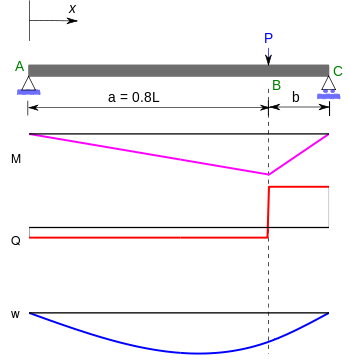 | |
en | ||
Vigas en voladizo
Otra clase importante de problemas involucra vigas en voladizo . Los momentos de flexión ( ), fuerzas de corte ( ) y deflexiones ( ) para una viga en voladizo sometida a una carga puntual en el extremo libre y una carga uniformemente distribuida se dan en la siguiente tabla. [5]
| Distribución | Valor máximo | |
|---|---|---|
| Viga en voladizo con carga en el extremo |  | |
| Viga en voladizo con carga distribuida uniformemente | 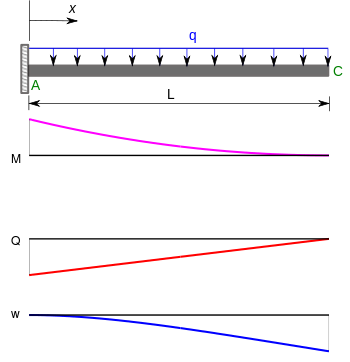 | |
Las soluciones para otras configuraciones comúnmente encontradas están disponibles en libros de texto sobre mecánica de materiales y manuales de ingeniería.
Vigas estáticamente indeterminadas
Los momentos de flexión y las fuerzas de corte en vigas de Euler-Bernoulli a menudo se pueden determinar directamente utilizando el equilibrio estático de fuerzas y momentos . Sin embargo, para ciertas condiciones de contorno, el número de reacciones puede superar el número de ecuaciones de equilibrio independientes. [5] Estas vigas se denominan estáticamente indeterminadas .
Las vigas empotradas que se muestran en la figura siguiente son estáticamente indeterminadas. Para determinar las tensiones y deflexiones de dichas vigas, el método más directo es resolver la ecuación de vigas de Euler-Bernoulli con las condiciones de contorno adecuadas. Sin embargo, las soluciones analíticas directas de la ecuación de vigas solo son posibles para los casos más simples. Por lo tanto, a menudo se utilizan técnicas adicionales, como la superposición lineal, para resolver problemas de vigas estáticamente indeterminadas.
El método de superposición implica sumar las soluciones de una serie de problemas estáticamente determinados que se eligen de manera que las condiciones de contorno para la suma de los problemas individuales se sumen a las del problema original.
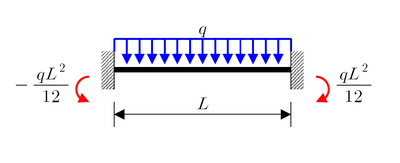 (a) Carga uniformemente distribuida q . | 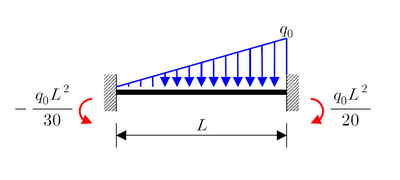 (b) Carga distribuida linealmente con q máximo 0 |
 (c) Carga concentrada P |  (d) Momento M 0 |
Otro problema de viga estáticamente indeterminada que se presenta con frecuencia es el de la viga en voladizo con el extremo libre apoyado sobre un rodillo. [5] Los momentos de flexión, las fuerzas de corte y las deflexiones de dicha viga se enumeran a continuación:
| Distribución | Valor máximo |  |
|---|---|---|
Extensiones
Las suposiciones cinemáticas sobre las que se basa la teoría de vigas de Euler-Bernoulli permiten extenderla a análisis más avanzados. La superposición simple permite la carga transversal tridimensional. El uso de ecuaciones constitutivas alternativas puede permitir la deformación viscoelástica o plástica de la viga. La teoría de vigas de Euler-Bernoulli también se puede extender al análisis de vigas curvas, pandeo de vigas , vigas compuestas y deflexión de vigas geométricamente no lineal.
La teoría de vigas de Euler-Bernoulli no tiene en cuenta los efectos de la deformación cortante transversal . Como resultado, subestima las deflexiones y sobreestima las frecuencias naturales. Para vigas delgadas (relaciones entre la longitud de la viga y el espesor del orden de 20 o más), estos efectos son de menor importancia. Sin embargo, para vigas gruesas, estos efectos pueden ser significativos. Se han desarrollado teorías de vigas más avanzadas, como la teoría de vigas de Timoshenko (desarrollada por el científico nacido en Rusia Stephen Timoshenko ), para tener en cuenta estos efectos.
Grandes desviaciones

La teoría original de Euler-Bernoulli es válida únicamente para deformaciones infinitesimales y rotaciones pequeñas. La teoría puede extenderse de manera sencilla a problemas que impliquen rotaciones moderadamente grandes, siempre que la deformación se mantenga pequeña, utilizando las deformaciones de von Kármán . [8]
Las hipótesis de Euler-Bernoulli de que las secciones planas permanecen planas y normales al eje de la viga conducen a desplazamientos de la forma
Utilizando la definición de la deformación de Green lagrangiana de la teoría de deformaciones finitas , podemos encontrar las deformaciones de von Kármán para la viga que son válidas para rotaciones grandes pero deformaciones pequeñas descartando todos los términos de orden superior (que contienen más de dos campos) excepto Las deformaciones resultantes toman la forma:
A partir del principio del trabajo virtual , el equilibrio de fuerzas y momentos en las vigas nos da las ecuaciones de equilibrio
donde es la carga axial, es la carga transversal, y
Para cerrar el sistema de ecuaciones necesitamos las ecuaciones constitutivas que relacionan las tensiones con las deformaciones (y por tanto las tensiones con los desplazamientos). Para grandes rotaciones y pequeñas deformaciones estas relaciones son
dónde
La cantidad es la rigidez extensional , es la rigidez extensional-flectiva acoplada y es la rigidez flectora .
Para la situación en la que la viga tiene una sección transversal uniforme y no tiene carga axial, la ecuación gobernante para una viga de Euler-Bernoulli de gran rotación es
Véase también
- Mecánica aplicada
- Doblado
- Momento flector
- Pandeo
- Rigidez flexural
- Teoría generalizada de vigas
- Teoría de placas
- Teoría del sándwich
- Diagrama de esfuerzo cortante y de momento
- Función de singularidad
- Deformación (ciencia de los materiales)
- Teoría de la viga de Timoshenko
- Teorema de los tres momentos (teorema de Clapeyron)
- Prueba de flexión de tres puntos
Referencias
Notas
- ^ Para una viga de Euler-Bernoulli que no está bajo ninguna carga axial, este eje se denomina eje neutro .
Citas
- ^ Timoshenko, S. (1953). Historia de la resistencia de los materiales . Nueva York: McGraw-Hill.
- ^ Truesdell, C. (1960). La mecánica racional de cuerpos flexibles o elásticos 1638-1788 . Venditioni Exponunt Orell Fussli Turici.
- ^ Ballarini, Roberto (18 de abril de 2003). "The Da Vinci-Euler-Bernoulli Beam Theory?". Revista de Ingeniería Mecánica en Línea . Archivado desde el original el 23 de junio de 2006. Consultado el 22 de julio de 2006 .
- ^ Han, Seon M.; Benaroya, Haym; Wei, Timothy (22 de marzo de 1999). "Dinámica de vigas que vibran transversalmente utilizando cuatro teorías de ingeniería" (PDF) . Journal of Sound and Vibration . 225 (5). Academic Press: 935. Bibcode :1999JSV...225..935H. doi :10.1006/jsvi.1999.2257. Archivado desde el original (PDF) el 20 de julio de 2011 . Consultado el 15 de abril de 2007 .
- ^ abcdefgh Gere, JM; Timoshenko, SP (1997). Mecánica de materiales . PWS.
- ^ Caresta, Mauro. "Vibraciones de una viga libre-libre" (PDF) . Consultado el 20 de marzo de 2019 .
- ^ Irvine, Tom. "Viga fijada con pasadores" . Consultado el 13 de octubre de 2024 .
- ^ Reddy, JN (2007). Análisis de elementos finitos no lineales . Oxford University Press.
Lectura adicional
- EA Witmer (1991–1992). "Teoría elemental de vigas de Bernoulli-Euler". Apuntes del curso de ingeniería unificada del MIT . págs. 5–114 a 5–164.
Enlaces externos
- Tensión y deflexión de vigas, tablas de deflexión de vigas











































![{\displaystyle S=\int _{t_{1}}^{t_{2}}\int _{0}^{L}\left[{\frac {1}{2}}\mu \left({\frac {\parcial w}{\parcial t}}\right)^{2}-{\frac {1}{2}}EI\left({\frac {\parcial ^{2}w}{\parcial x^{2}}}\right)^{2}+q(x)w(x,t)\right]dxdt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/344adbcade0f3dddbc62314c2f884550f7288ec8)










![{\displaystyle w(x,t)={\text{Re}}[{\hat {w}}(x)~e^{-i\omega t}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9107e40d745b3d23b0e79b6ee1620bbf6f123cc)















![{\displaystyle {\hat {w}}_{n}=A_{1}\left[(\cosh \beta _{n}x-\cos \beta _{n}x)+{\frac {\cos \beta _{n}L+\cosh \beta _{n}L}{\sin \beta _{n}L+\sinh \beta _{n}L}}(\sin \beta _{n}x-\sinh \beta _{n}x)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62ed25555fac4df06030b671816f9f935e80b796)












![{\displaystyle {\hat {w}}_{n}=A_{1}{\Bigl [}(\cos \beta _ {n}x+\cosh \beta _ {n}x)-{\frac {\ cos \beta _{n}L-\cosh \beta _{n}L}{\sin \beta _{n}L-\sinh \beta _{n}L}}(\sin \beta _{n} x+\sinh \beta _{n}x){\Bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9490c324727f67e03fc51eef592533fba83c755f)



























































































![{\displaystyle M_{\mathrm {máx}}={\cfrac {qL^{2}}{300}}[3{\sqrt {30}}-10]~;~~w_{\mathrm {máx}}={\cfrac {qL^{4}}{2500EI}}[75-7{\sqrt {105}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c645a45da08a7383e7f7cfccc1fe79f26642657)








![{\displaystyle {\begin{aligned}\varepsilon _{11}&={\cfrac {\mathrm {d} {u_{0}}}{\mathrm {d} {x}}}-z{\cfrac { \mathrm {d} ^{2}{w_{0}}}{\mathrm {d} {x^{2}}}}+{\frac {1}{2}}\left[\left({\ cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}-z{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{ 2}}}\right)^{2}+\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]\aprox {\cfrac {\mathrm {d} {u_{0}}}{\mathrm {d} {x}}}-z{\cfrac {\mathrm {d} ^{2}{w_{0}}}{\mathrm {d} {x^{ 2}}}}+{\frac {1}{2}}\left({\frac {\mathrm {d} {w_{0}}}{\mathrm {d} {x}}}\right)^ {2}\\[0.25em]\varepsilon _{22}&=0\\[0.25em]\varepsilon _{33}&={\frac {1}{2}}\left({\frac {\ mathrm {d} {w_{0}}}{\mathrm {d} {x}}}\right)^{2}\\[0.25em]\varepsilon _{23}&=0\\[0.25em] \varepsilon _{31}&=-{\frac {1}{2}}\left[\left({\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}-z{\ cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\derecha)\izquierda({\cfrac {\mathrm {d} w_{0}}{ \mathrm {d} x}}\right)\right]\aproximadamente 0\\[0,25em]\varepsilon _{12}&=0.\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bae862e70eea1ec7856a6c9913cec5d0247e999e)



![{\displaystyle {\begin{aligned}N_{xx}&=A_{xx}[{\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}+{\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]-B_{xx}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\\M_{xx}&=B_{xx}[{\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}+{\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]-D_{xx}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf5963b78c161027653b39e6d907f2624d711419)





