Función ext.
En matemáticas , los funtores Ext son los funtores derivados del funtor Hom . Junto con el funtor Tor , Ext es uno de los conceptos centrales del álgebra homológica , en la que se utilizan ideas de la topología algebraica para definir invariantes de estructuras algebraicas. La cohomología de grupos , las álgebras de Lie y las álgebras asociativas se pueden definir en términos de Ext. El nombre proviene del hecho de que el primer grupo Ext Ext 1 clasifica las extensiones de un módulo por otro.
En el caso especial de los grupos abelianos , Ext fue introducido por Reinhold Baer (1934). Fue nombrado por Samuel Eilenberg y Saunders MacLane (1942), y aplicado a la topología (el teorema del coeficiente universal para cohomología ). Para módulos sobre cualquier anillo , Ext fue definido por Henri Cartan y Eilenberg en su libro de 1956 Homological Algebra . [1]
Definición
Sea R un anillo y sea R -Mod la categoría de módulos sobre R . (Esto puede significar tanto R -módulos izquierdos como R -módulos derechos.) Para un R -módulo fijo A , sea T ( B ) = Hom R ( A , B ) para B en R -Mod. (Aquí Hom R ( A , B ) es el grupo abeliano de funciones R -lineales de A a B ; este es un R -módulo si R es conmutativo .) Este es un funtor exacto izquierdo de R -Mod a la categoría de grupos abelianos Ab, y por lo tanto tiene funtores derivados derechos R i T . Los grupos Ext son los grupos abelianos definidos por
para un entero i . Por definición, esto significa: tomar cualquier resolución inyectiva
elimina el término B y forma el complejo de cocadena :
Para cada entero i , ExtYo
R( A , B ) es la cohomología de este complejo en la posición i . Es cero para i negativo. Por ejemplo, Ext0
R( A , B ) es el núcleo del mapa Hom R ( A , I 0 ) → Hom R ( A , I 1 ), que es isomorfo a Hom R ( A , B ).
Una definición alternativa utiliza el funtor G ( A )=Hom R ( A , B ), para un R -módulo B fijo . Este es un funtor contravariante , que puede verse como un funtor exacto por la izquierda de la categoría opuesta ( R -Mod) op a Ab. Los grupos Ext se definen como los funtores derivados por la derecha R i G :
Es decir, elija cualquier resolución proyectiva.
elimina el término A y forma el complejo de cocadena:
Luego ExtYo
R( A , B ) es la cohomología de este complejo en la posición i .
Uno podría preguntarse por qué la elección de la resolución se ha dejado tan vaga. De hecho, Cartan y Eilenberg demostraron que estas construcciones son independientes de la elección de la resolución proyectiva o inyectiva, y que ambas construcciones producen los mismos grupos Ext. [2] Además, para un anillo fijo R , Ext es un funtor en cada variable (contravariante en A , covariante en B ).
Para un anillo conmutativo R y R -módulos A y B , ExtYo
R( A , B ) es un módulo R (usando que Hom R ( A , B ) es un módulo R en este caso). Para un anillo no conmutativo R , ExtYo
R( A , B ) es sólo un grupo abeliano, en general. Si R es un álgebra sobre un anillo S (lo que significa en particular que S es conmutativo), entonces ExtYo
R( A , B ) es al menos un módulo S.
Propiedades de Ext
A continuación se presentan algunas de las propiedades y cálculos básicos de los grupos Ext. [3]
- Extensión0
R( A , B ) ≅ Hom R ( A , B ) para cualesquiera R -módulos A y B .
- ExtensiónYo
R( A , B ) = 0 para todo i > 0 si el R -módulo A es proyectivo (por ejemplo, libre ) o si B es inyectivo .
- Los recíprocos también son válidos:
- Si Ext1
R( A , B ) = 0 para todo B , entonces A es proyectiva (y por lo tanto ExtYo
R( A , B ) = 0 para todo i > 0). - Si Ext1
R( A , B ) = 0 para todo A , entonces B es inyectiva (y por lo tanto ExtYo
R( A , B ) = 0 para todo i > 0).
- Si Ext1
- para todo i ≥ 2 y todos los grupos abelianos A y B. [4 ]
- Generalizando el ejemplo anterior, para todo i ≥ 2 si R es un dominio ideal principal .
- Si R es un anillo conmutativo y u en R no es un divisor de cero , entonces
- para cualquier módulo R B . Aquí B [ u ] denota el subgrupo de u -torsión de B , { x ∈ B : ux = 0}. Si tomamos R como el anillo de números enteros, este cálculo se puede utilizar para calcular cualquier grupo abeliano A finitamente generado .
- Generalizando el ejemplo anterior, se pueden calcular grupos Ext cuando el primer módulo es el cociente de un anillo conmutativo por cualquier secuencia regular , utilizando el complejo de Koszul . [5] Por ejemplo, si R es el anillo polinomial k [ x 1 ,..., x n ] sobre un cuerpo k , entonces Ext*
R( k , k ) es el álgebra exterior S sobre k en n generadores en Ext 1 . Además, Ext*
S( k , k ) es el anillo polinomial R ; este es un ejemplo de dualidad de Koszul .
- Por las propiedades generales de los funtores derivados, hay dos secuencias exactas básicas para Ext. [6] Primero, una secuencia exacta corta 0 → K → L → M → 0 de R -módulos induce una secuencia exacta larga de la forma
- para cualquier R -módulo A . Además, una secuencia exacta corta 0 → K → L → M → 0 induce una secuencia exacta larga de la forma
- para cualquier R -módulo B .
- Ext toma sumas directas (posiblemente infinitas) en la primera variable y productos en la segunda variable para convertirlos en productos. [7] Es decir:
- Sea A un módulo finitamente generado sobre un anillo noetheriano conmutativo R . Entonces Ext conmuta con localización , en el sentido de que para cada conjunto multiplicativamente cerrado S en R , cada R -módulo B , y cada entero i , [8]
Extensión y extensiones
Equivalencia de extensiones
Los grupos Ext derivan su nombre de su relación con las extensiones de módulos. Dados los R -módulos A y B , una extensión de A por B es una secuencia corta y exacta de R -módulos.
Dos extensiones
Se dice que son equivalentes (como extensiones de A por B ) si existe un diagrama conmutativo :
Nótese que el lema de los cinco implica que la flecha del medio es un isomorfismo. Una extensión de A por B se llama división si es equivalente a la extensión trivial
Existe una correspondencia biunívoca entre las clases de equivalencia de extensiones de A por B y elementos de Ext.1
R( A , B ). [9] La extensión trivial corresponde al elemento cero de Ext1
R( A , B ).
La suma de extensiones de Baer
La suma de Baer es una descripción explícita de la estructura del grupo abeliano en Ext1
R( A , B ), visto como el conjunto de clases de equivalencia de extensiones de A por B . [10] Es decir, dadas dos extensiones
y
primero forma el retroceso sobre ,
Luego forma el módulo del cociente
La suma de Baer de E y E′ es la extensión
donde esta el primer mapa y el segundo es .
Hasta equivalencia de extensiones, la suma de Baer es conmutativa y tiene como elemento identidad la extensión trivial. El negativo de una extensión 0 → B → E → A → 0 es la extensión que involucra el mismo módulo E , pero con el homomorfismo B → E reemplazado por su negativo.
Construcción de Ext en categorías abelianas
Nobuo Yoneda definió los grupos abelianos Exten
C( A , B ) para objetos A y B en cualquier categoría abeliana C ; esto concuerda con la definición en términos de resoluciones si C tiene suficientes proyectivas o suficientes inyectivas . Primero, Ext0
C( A , B ) = Hom C ( A , B ). A continuación, Ext1
C( A , B ) es el conjunto de clases de equivalencia de extensiones de A por B , formando un grupo abeliano bajo la suma de Baer. Finalmente, los grupos Ext superiores Exten
C( A , B ) se definen como clases de equivalencia de n-extensiones , que son secuencias exactas
bajo la relación de equivalencia generada por la relación que identifica dos extensiones
si hay mapas para todos los m en {1, 2, ..., n } de modo que cada cuadrado resultante conmuta , es decir, si hay un mapa de cadena que es la identidad en A y B.
La suma de Baer de dos n -extensiones como las anteriores se forma dejando que sea el retroceso de y sobre A , y sea el empuje de y debajo de B . [11] Entonces la suma de Baer de las extensiones es
La categoría derivada y el producto Yoneda
Un punto importante es que los grupos Ext en una categoría abeliana C pueden verse como conjuntos de morfismos en una categoría asociada a C , la categoría derivada D ( C ). [12] Los objetos de la categoría derivada son complejos de objetos en C . Específicamente, uno tiene
donde un objeto de C se considera un complejo concentrado en grado cero, y [ i ] significa desplazar un complejo i pasos hacia la izquierda. A partir de esta interpretación, existe una función bilineal , a veces llamada producto de Yoneda :
que es simplemente la composición de morfismos en la categoría derivada.
El producto de Yoneda también se puede describir en términos más elementales. Para i = j = 0, el producto es la composición de funciones en la categoría C. En general, el producto se puede definir uniendo dos extensiones de Yoneda.
Alternativamente, el producto de Yoneda se puede definir en términos de resoluciones. (Esto se acerca a la definición de la categoría derivada). Por ejemplo, sea R un anillo, con R -módulos A , B , C , y sean P , Q y T resoluciones proyectivas de A , B , C . Entonces ExtYo
R( A , B ) se puede identificar con el grupo de clases de homotopía de cadenas de mapas de cadena P → Q [ i ]. El producto de Yoneda se da componiendo mapas de cadena:
Por cualquiera de estas interpretaciones, el producto de Yoneda es asociativo. Como resultado, es un anillo graduado , para cualquier R -módulo A . Por ejemplo, esto da la estructura de anillo en cohomología de grupo ya que esto puede verse como . También por asociatividad del producto de Yoneda: para cualquier R -módulo A y B , es un módulo sobre .
Casos especiales importantes
- La cohomología de grupos se define por , donde G es un grupo, M es una representación de G sobre los números enteros y es el anillo de grupo de G.
- Para un álgebra A sobre un cuerpo k y un A - bimódulo M , la cohomología de Hochschild se define por
- La cohomología del álgebra de Lie se define por , donde es un álgebra de Lie sobre un anillo conmutativo k , M es un -módulo y es el álgebra envolvente universal .
- Para un espacio topológico X , la cohomología de haces se puede definir como Aquí Ext se toma en la categoría abeliana de haces de grupos abelianos en X , y es el haz de funciones de valor localmente constante .
- Para un anillo local noetheriano conmutativo R con cuerpo de residuos k , es el álgebra envolvente universal de un álgebra de Lie graduada π*( R ) sobre k , conocida como el álgebra de Lie de homotopía de R . (Para ser precisos, cuando k tiene característica 2, π*( R ) tiene que ser visto como un "álgebra de Lie ajustada". [13] ) Hay un homomorfismo natural de álgebras de Lie graduadas desde la cohomología de André–Quillen D *( k / R , k ) a π*( R ), que es un isomorfismo si k tiene característica cero. [14]
Véase también
Notas
- ^ Weibel (1999); Cartan y Eilenberg (1956), sección VI.1.
- ^ Weibel (1994), secciones 2.4 y 2.5 y Teorema 2.7.6.
- ^ Weibel (1994), Capítulos 2 y 3.
- ^ Weibeil (1994), Lema 3.3.1.
- ^ Weibel (1994), sección 4.5.
- ^ Weibel (1994), Definición 2.1.1.
- ^ Weibel (1994), Proposición 3.3.4.
- ^ Weibel (1994), Proposición 3.3.10.
- ^ Weibel (1994), Teorema 3.4.3.
- ^ Weibel (1994), Corolario 3.4.5.
- ^ Weibel (1994), Vists 3.4.6. Se incluyen algunas correcciones menores en la sección de erratas.
- ^ Weibel (1994), secciones 10.4 y 10.7; Gelfand y Manin (2003), Capítulo III.
- ^ Sjödin (1980), Notación 14.
- ^ Avramov (2010), sección 10.2.
Referencias
- Avramov, Luchezar (2010), "Resoluciones libres infinitas", Seis conferencias sobre álgebra conmutativa , Birkhäuser , pp. 1–108, doi :10.1007/978-3-0346-0329-4_1, ISBN 978-3-7643-5951-5, Sr. 2641236
- Baer, Reinhold (1934), "Erweiterung von Gruppen und ihren Isomorphismen", Mathematische Zeitschrift , 38 (1): 375–416, doi :10.1007/BF01170643, Zbl 0009.01101
- Cartan, Henri ; Eilenberg, Samuel (1999) [1956], Álgebra homológica , Princeton: Princeton University Press , ISBN 0-691-04991-2, Sr. 0077480
- Eilenberg, Samuel ; MacLane, Saunders (1942), "Extensiones de grupo y homología", Anales de Matemáticas , 43 (4): 757–931, doi :10.2307/1968966, JSTOR 1968966, MR 0007108
- Gelfand, Serguéi I.; Manin, Yuri Ivanovich (2003), Métodos de álgebra homológica , Berlín, Nueva York: Springer-Verlag , doi :10.1007/978-3-662-12492-5, ISBN 978-3-540-43583-9, Sr. 1950475
- Sjödin, Gunnar (1980), "Álgebras y derivaciones de Hopf", Journal of Algebra , 64 : 218–229, doi : 10.1016/0021-8693(80)90143-X , MR 0575792
- Weibel, Charles A. (1994). Introducción al álgebra homológica . Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. Sr. 1269324. OCLC 36131259.
- Weibel, Charles A. (1999), "Historia del álgebra homológica" (PDF) , Historia de la topología , Ámsterdam: Holanda Septentrional, pp. 797–836, ISBN 9780444823755, Sr. 1721123








![{\displaystyle \operatorname {Ext} _{R}^{i}(R/(u),B)\cong {\begin{cases}B[u]&i=0\\B/uB&i=1\\0&{\text{de lo contrario,}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d29b19b92e3188770f876e89fe5d69f61f2bb030)









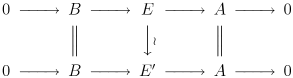

![{\displaystyle 0\to B{\xrightarrow[{f}]{}}E{\xrightarrow[{g}]{}}A\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99b91ef9769c22705bb158052b57276636e7906c)
![{\displaystyle 0\to B{\xrightarrow[{f'}]{}}E'{\xrightarrow[{g'}]{}}A\to 0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3c3b1f07bd8dcc1d933bb0a1b72b397a6e885e9)




![{\displaystyle b\mapsto [(f(b),0)]=[(0,f'(b))]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee75b87481bf9de19754e30ff4b98f9e3a93c53f)













![{\displaystyle \operatorname {Ext} _{\mathbf {C} }^{i}(A,B)=\operatorname {Hom} _{D({\mathbf {C} })}(A,B[i]),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd4f0a89006dc8d51c99160bf062be7b92891c2f)

![{\displaystyle P\a Q[i]\a T[i+j].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e1db5574c44feacd2e3448b888bb92c98bb8c17)


![{\displaystyle \operatorname {Ext} _{\mathbb {Z} [G]}^{*}(\mathbb {Z} ,\mathbb {Z} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caa2d03e117e399c9fc5a96b1e4383be50277a2b)

![{\displaystyle H^{*}(G,M)=\nombredeloperador {Ext} _{\mathbb {Z} [G]}^{*}(\mathbb {Z} ,M)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75ea5c28b67c0bc2f3dea33b55aa97d33977f830)
![{\displaystyle \mathbb {Z} [G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f40260c366fc309a5872899d2ea34cf094855857)






