Modelado de diodos

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Modelado de diodos» – noticias  · periódicos  · libros  · académico  · JSTOR ( octubre de 2014 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En electrónica , el modelado de diodos se refiere a los modelos matemáticos utilizados para aproximar el comportamiento real de los diodos reales y permitir los cálculos y el análisis de circuitos. La curva I - V de un diodo no es lineal .

Un modelo físico muy preciso, pero complicado, compone la curva IV a partir de tres exponenciales con una pendiente ligeramente diferente (es decir, factor de idealidad ), que corresponden a diferentes mecanismos de recombinación en el dispositivo; ^[1] para corrientes muy grandes y muy pequeñas, la curva puede continuar mediante segmentos lineales (es decir, comportamiento resistivo).

En una aproximación relativamente buena, un diodo se modela mediante la ley de diodos de Shockley monoexponencial . Esta no linealidad aún complica los cálculos en circuitos que involucran diodos, por lo que a menudo se utilizan modelos aún más simples.

Este artículo analiza el modelado de diodos de unión pn , pero las técnicas pueden generalizarse a otros diodos de estado sólido .

La ecuación del diodo Shockley relaciona la corriente del diodo de una unión pn con el voltaje del diodo . Esta relación es la característica IV del diodo :${\displaystyle I}$$Estilo de visualización VD$

${\displaystyle I=I_{S}\left(e^{\frac {V_{D}}{nV_{\text{T}}}}-1\right)}$,

donde es la corriente de saturación o corriente de escala del diodo (la magnitud de la corriente que fluye para valores negativos superiores a unos pocos , típicamente 10 ⁻¹² A). La corriente de escala es proporcional al área de la sección transversal del diodo. Continuando con los símbolos: es el voltaje térmico ( , aproximadamente 26 mV a temperaturas normales),${\displaystyle I_{S}}$$Estilo de visualización VD$${\displaystyle V_{\text{T}}}$ ${\displaystyle V_{\text{T}}}$${\displaystyle kT/q}$y se conoce como factor de idealidad del diodo (para los diodos de silicio es aproximadamente 1 a 2).${\estilo de visualización n}$${\estilo de visualización n}$

Cuando la fórmula se puede simplificar a:${\displaystyle V_{D}\gg nV_{\text{T}}}$

${\displaystyle I\approx I_{S}\cdot e^{\frac {V_{D}}{nV_{\text{T}}}}}$.

Sin embargo, esta expresión es sólo una aproximación de una característica IV más compleja. Su aplicabilidad es particularmente limitada en el caso de uniones ultra superficiales, para las cuales existen mejores modelos analíticos. ^[2]

Para ilustrar las complicaciones en el uso de esta ley, considere el problema de encontrar el voltaje a través del diodo en la Figura 1.

Como la corriente que fluye a través del diodo es la misma que la corriente que circula por todo el circuito, podemos plantear otra ecuación. Según las leyes de Kirchhoff , la corriente que fluye en el circuito es

${\displaystyle I={\frac {V_{S}-V_{D}}{R}}}$.

Estas dos ecuaciones determinan la corriente y el voltaje del diodo. Para resolver estas dos ecuaciones, podríamos sustituir la corriente de la segunda ecuación en la primera ecuación y luego intentar reorganizar la ecuación resultante para obtener en términos de . Una dificultad con este método es que la ley del diodo no es lineal. No obstante, se puede obtener una fórmula que exprese directamente en términos de sin involucrar utilizando la función W de Lambert , que es la función inversa de , es decir, . Esta solución se analiza a continuación.${\displaystyle I}$$Estilo de visualización VD$${\displaystyle V_{S}}$${\displaystyle I}$${\displaystyle V_{S}}$$Estilo de visualización VD$${\displaystyle f(w)=nosotros^{w}}$${\displaystyle w=W(f)}$

Se puede obtener una expresión explícita para la corriente del diodo en términos de la función W de Lambert (también llamada función Omega). ^[3] A continuación se presenta una guía para estas manipulaciones. Se introduce una nueva variable como${\estilo de visualización w}$

${\displaystyle w={\frac {I_{S}R}{nV_{\text{T}}}}({\frac {I}{I_{S}}}+1\right)}$.

A continuación las sustituciones :${\displaystyle I/I_{S}=e^{V_{D}/nV_{\text{T}}}-1}$

${\displaystyle we^{w}={\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{D}}{nV_{\text{T}}}}e^{{\frac {I_{S}R}{nV_{\text{T}}}}\left({\frac {I}{I_{S}}}+1\right)}}$

y :${\displaystyle V_{D}=V_{S}-IR}$

${\displaystyle we^{w}={\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{S}}{nV_{\text{T}}}}e^{\frac {-IR}{nV_{\text{T}}}}e^{\frac {IRI_{S}}{nV_{\text{T}}I_{S}}}e^{\frac {I_{S}R}{nV_{\text{T}}}}}$

La reordenación de la ley del diodo en términos de w se convierte en:

${\displaystyle we^{w}={\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{s}+I_{s}R}{nV_{\text{T}}}}}$,

que utilizando la función Lambert se convierte en${\estilo de visualización W}$

${\displaystyle w=W\left({\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{s}+I_{s}R}{nV_{\text{T}}}}\right)}$.

La solución explícita final es

${\displaystyle I={\frac {nV_{\text{T}}}{R}}W\left({\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{s}+I_{s}R}{nV_{\text{T}}}}\right)-I_{S}}$.

Con las aproximaciones (válidas para los valores más comunes de los parámetros) y , esta solución se convierte en${\displaystyle I_{s}R\ll V_{S}}$${\displaystyle I/I_{S}\gg 1}$

${\displaystyle I\approx {\frac {nV_{\text{T}}}{R}}W\left({\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{s}}{nV_{\text{T}}}}\right)}$.

Una vez determinada la corriente, el voltaje del diodo se puede encontrar utilizando cualquiera de las otras ecuaciones.

Para valores grandes de x, se puede aproximar mediante . Para parámetros físicos y resistencias comunes, será del orden de 10 ⁴⁰ .${\displaystyle W(x)}$${\displaystyle W(x)=\ln x-\ln \ln x+o(1)}$${\displaystyle {\frac {I_{S}R}{nV_{\text{T}}}}e^{\frac {V_{s}}{nV_{\text{T}}}}}$

El voltaje del diodo se puede encontrar en términos de para cualquier conjunto particular de valores mediante un método iterativo utilizando una calculadora o computadora. ^[4] La ley del diodo se reorganiza dividiendo por y sumando 1. La ley del diodo se convierte en${\displaystyle V_{D}}$${\displaystyle V_{S}}$${\displaystyle I_{S}}$

${\displaystyle e^{\frac {V_{D}}{nV_{\text{T}}}}={\frac {I}{I_{S}}}+1}$.

Al tomar los logaritmos naturales de ambos lados se elimina el exponencial y la ecuación se convierte en

${\displaystyle {\frac {V_{D}}{nV_{\text{T}}}}=\ln \left({\frac {I}{I_{S}}}+1\right)}$.

Para cualquier , esta ecuación determina . Sin embargo, también debe satisfacer la ecuación de la ley de Kirchhoff, dada anteriormente. Esta expresión se sustituye por para obtener${\displaystyle I}$${\displaystyle V_{D}}$${\displaystyle I}$${\displaystyle I}$

${\displaystyle {\frac {V_{D}}{nV_{\text{T}}}}=\ln \left({\frac {V_{S}-V_{D}}{RI_{S}}}+1\right)}$,

o

${\displaystyle V_{D}=nV_{\text{T}}\ln \left({\frac {V_{S}-V_{D}}{RI_{S}}}+1\right)}$.

El voltaje de la fuente es un valor dado conocido, pero está en ambos lados de la ecuación, lo que obliga a una solución iterativa: se adivina un valor inicial para y se coloca en el lado derecho de la ecuación. Al realizar las diversas operaciones en el lado derecho, obtenemos un nuevo valor para . Este nuevo valor ahora se sustituye en el lado derecho, y así sucesivamente. Si esta iteración converge , los valores de se acercan cada vez más entre sí a medida que continúa el proceso, y podemos detener la iteración cuando la precisión sea suficiente. Una vez que se encuentra, se puede encontrar a partir de la ecuación de la ley de Kirchhoff.${\displaystyle V_{S}}$${\displaystyle V_{D}}$${\displaystyle V_{D}}$${\displaystyle V_{D}}$${\displaystyle V_{D}}$${\displaystyle V_{D}}$${\displaystyle I}$

A veces, un procedimiento iterativo depende críticamente de la primera aproximación. En este ejemplo, casi cualquier aproximación servirá, digamos . A veces, un procedimiento iterativo no converge en absoluto: en este problema, una iteración basada en la función exponencial no converge, y es por eso que las ecuaciones se reorganizaron para utilizar un logaritmo. Encontrar una formulación iterativa convergente es un arte, y cada problema es diferente.${\displaystyle V_{D}=600\,{\text{mV}}}$

El análisis gráfico es una forma sencilla de obtener una solución numérica de las ecuaciones trascendentales que describen el diodo. Como ocurre con la mayoría de los métodos gráficos, tiene la ventaja de que es fácil de visualizar. Al trazar las curvas I - V , es posible obtener una solución aproximada con cualquier grado arbitrario de precisión. Este proceso es el equivalente gráfico de los dos enfoques anteriores, que son más fáciles de implementar en la computadora.

Este método representa gráficamente las dos ecuaciones de corriente y tensión y el punto de intersección de las dos curvas satisface ambas ecuaciones, lo que da el valor de la corriente que fluye a través del circuito y la tensión a través del diodo. La figura ilustra dicho método.

En la práctica, el método gráfico es complicado y poco práctico para circuitos complejos. Otro método para modelar un diodo se denomina modelado lineal por partes (PWL) . En matemáticas, esto significa tomar una función y descomponerla en varios segmentos lineales. Este método se utiliza para aproximar la curva característica del diodo como una serie de segmentos lineales. El diodo real se modela como 3 componentes en serie: un diodo ideal, una fuente de voltaje y una resistencia .

La figura muestra una curva IV de diodo real que se aproxima mediante un modelo lineal por partes de dos segmentos. Normalmente, el segmento de línea inclinado se elegiría tangente a la curva del diodo en el punto Q. Luego, la pendiente de esta línea está dada por el recíproco de la resistencia de pequeña señal del diodo en el punto Q.

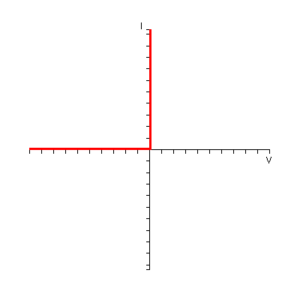
En primer lugar, consideremos un diodo idealizado matemáticamente. En un diodo ideal de este tipo, si el diodo está polarizado inversamente, la corriente que fluye a través de él es cero. Este diodo ideal comienza a conducir a 0 V y para cualquier voltaje positivo fluye una corriente infinita y el diodo actúa como un cortocircuito. Las características IV de un diodo ideal se muestran a continuación:

Consideremos ahora el caso en el que agregamos una fuente de voltaje en serie con el diodo en la forma que se muestra a continuación:

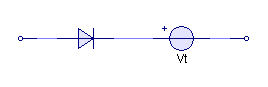
Cuando está polarizado directamente, el diodo ideal es simplemente un cortocircuito y cuando está polarizado inversamente, un circuito abierto.

Si el ánodo del diodo está conectado a 0  V, el voltaje en el cátodo será Vt y, por lo tanto, el potencial en el cátodo será mayor que el potencial en el ánodo y el diodo estará polarizado en forma inversa. Para que el diodo conduzca, el voltaje en el ánodo deberá llevarse a Vt . Este circuito se aproxima al voltaje de corte presente en los diodos reales. La característica IV combinada de este circuito se muestra a continuación:

El modelo de diodo Shockley se puede utilizar para predecir el valor aproximado de .${\displaystyle V_{t}}$

${\displaystyle {\begin{aligned}&I=I_{S}\left(e^{\frac {V_{D}}{n\cdot V_{\text{T}}}}-1\right)\\\Leftrightarrow {}&\ln \left(1+{\frac {I}{I_{S}}}\right)={\frac {V_{D}}{n\cdot V_{\text{T}}}}\\\Leftrightarrow {}&V_{D}=n\cdot V_{\text{T}}\ln \left(1+{\frac {I}{I_{S}}}\right)\approx n\cdot V_{\text{T}}\ln \left({\frac {I}{I_{S}}}\right)\\\Leftrightarrow {}&V_{D}\approx n\cdot V_{\text{T}}\cdot \ln {10}\cdot \log _{10}{\left({\frac {I}{I_{S}}}\right)}\end{aligned}}}$

Usando y :${\displaystyle n=1}$${\displaystyle T=25\,{\text{°C}}}$

${\displaystyle V_{D}\approx 0.05916\cdot \log _{10}{\left({\frac {I}{I_{S}}}\right)}}$

Los valores típicos de la corriente de saturación a temperatura ambiente son:

• ${\displaystyle I_{S}=10^{-12}}$para diodos de silicio;
• ${\displaystyle I_{S}=10^{-6}}$para diodos de germanio.

Como la variación de va con el logaritmo del cociente , su valor varía muy poco para una gran variación del cociente. El uso de logaritmos de base 10 hace que sea más fácil pensar en órdenes de magnitud.${\displaystyle V_{D}}$${\displaystyle {\frac {I}{I_{S}}}}$

Para una corriente de 1,0  mA:

• ${\displaystyle V_{D}\approx 0.53\,{\text{V}}}$para diodos de silicio (9 órdenes de magnitud);
• ${\displaystyle V_{D}\approx 0.18\,{\text{V}}}$para diodos de germanio (3 órdenes de magnitud).

Para una corriente de 100  mA:

• ${\displaystyle V_{D}\approx 0.65\,{\text{V}}}$para diodos de silicio (11 órdenes de magnitud);
• ${\displaystyle V_{D}\approx 0.30\,{\text{V}}}$para diodos de germanio (5 órdenes de magnitud).

Normalmente se utilizan valores de 0,6 o 0,7 voltios para los diodos de silicio. ^[5]

Lo último que se necesita es una resistencia para limitar la corriente, como se muestra a continuación:

La característica IV del circuito final se ve así:

Ahora, el diodo real se puede reemplazar por el diodo ideal combinado, la fuente de voltaje y la resistencia, y el circuito se modela utilizando solo elementos lineales. Si el segmento de línea inclinada es tangente a la curva del diodo real en el punto Q , este circuito aproximado tiene el mismo circuito de pequeña señal en el punto Q que el diodo real.

Cuando se desea una mayor precisión en el modelado de la característica de encendido del diodo, el modelo se puede mejorar duplicando el modelo PWL estándar. Este modelo utiliza dos diodos lineales por partes en paralelo, como una forma de modelar un solo diodo con mayor precisión.

Utilizando la ecuación de Shockley, la resistencia del diodo de pequeña señal del diodo se puede derivar sobre algún punto operativo ( punto Q ) donde la corriente de polarización de CC es y el voltaje aplicado en el punto Q es . ^{[6] Para comenzar, se encuentra la} conductancia de pequeña señal del diodo , es decir, el cambio en la corriente en el diodo causado por un pequeño cambio en el voltaje a través del diodo, dividido por este cambio de voltaje, es decir:${\displaystyle r_{D}}$${\displaystyle I_{Q}}$${\displaystyle V_{Q}}$ ${\displaystyle g_{D}}$

${\displaystyle g_{D}=\left.{\frac {dI}{dV}}\right|_{Q}={\frac {I_{s}}{n\cdot V_{\text{T}}}}e^{\frac {V_{Q}}{n\cdot V_{\text{T}}}}\approx {\frac {I_{Q}}{n\cdot V_{\text{T}}}}}$.

La última aproximación supone que la corriente de polarización es lo suficientemente grande como para que se pueda ignorar el factor 1 entre paréntesis de la ecuación del diodo Shockley. Esta aproximación es precisa incluso con voltajes bastante pequeños, porque el voltaje térmico a 300 K tiende a ser grande, lo que significa que la exponencial es muy grande.${\displaystyle I_{Q}}$ ${\displaystyle V_{\text{T}}\approx 25\,{\text{mV}}}$ ${\displaystyle V_{Q}/V_{\text{T}}}$

Teniendo en cuenta que la resistencia de pequeña señal es el recíproco de la conductancia de pequeña señal que se acaba de encontrar, la resistencia del diodo es independiente de la corriente alterna, pero depende de la corriente continua y se expresa como${\displaystyle r_{D}}$

${\displaystyle r_{D}={\frac {n\cdot V_{\text{T}}}{I_{Q}}}}$.

Se sabe que la carga en el diodo que transporta corriente es${\displaystyle I_{Q}}$

${\displaystyle Q=I_{Q}\tau _{F}+Q_{J}}$,

donde es el tiempo de tránsito hacia adelante de los portadores de carga: ^[6] El primer término en la carga es la carga en tránsito a través del diodo cuando fluye la corriente. El segundo término es la carga almacenada en la unión misma cuando se ve como un capacitor simple ; es decir, como un par de electrodos con cargas opuestas en ellos. Es la carga almacenada en el diodo en virtud de simplemente tener un voltaje a través de él, independientemente de cualquier corriente que conduzca.${\displaystyle \tau _{F}}$${\displaystyle I_{Q}}$

De manera similar a la anterior, la capacitancia del diodo es el cambio en la carga del diodo con el voltaje del diodo:

${\displaystyle C_{D}={\frac {dQ}{dV_{Q}}}={\frac {dI_{Q}}{dV_{Q}}}\tau _{F}+{\frac {dQ_{J}}{dV_{Q}}}\approx {\frac {I_{Q}}{V_{\text{T}}}}\tau _{F}+C_{J}}$,

donde es la capacitancia de la unión y el primer término se llama capacitancia de difusión , porque está relacionado con la corriente que se difunde a través de la unión.${\displaystyle C_{J}={\frac {dQ_{J}}{dV_{Q}}}}$

La ecuación del diodo Shockley tiene una exponencial de , lo que llevaría a esperar que el voltaje directo aumente con la temperatura. De hecho, este no suele ser el caso: a medida que aumenta la temperatura, aumenta la corriente de saturación y este efecto predomina. Por lo tanto, a medida que el diodo se calienta , el voltaje directo (para una corriente dada) disminuye .${\displaystyle V_{D}/(kT/q)}$${\displaystyle I_{S}}$

A continuación se presentan algunos datos experimentales detallados ^[7] que demuestran esto para un diodo de silicio 1N4005. De hecho, algunos diodos de silicio se utilizan como sensores de temperatura; por ejemplo, la serie CY7 de OMEGA tiene una tensión directa de 1,02  V en nitrógeno líquido (77  K), 0,54  V a temperatura ambiente y 0,29  V a 100 °C. ^[8]

Además, se produce un pequeño cambio en la banda prohibida de los parámetros del material con la temperatura. En el caso de los LED, este cambio en la banda prohibida también modifica su color: se desplazan hacia el extremo azul del espectro cuando se enfrían.

Dado que el voltaje directo del diodo cae a medida que aumenta su temperatura, esto puede provocar una fuga térmica debido al acaparamiento de corriente cuando se conecta en paralelo en circuitos de transistores bipolares (ya que la unión base-emisor de un BJT actúa como un diodo), donde una reducción en el voltaje directo base-emisor conduce a un aumento en la disipación de potencia del colector, lo que a su vez reduce aún más el voltaje directo base-emisor requerido.

• Transistor de unión bipolar
• Modelado de dispositivos semiconductores