Excentricidad (matemáticas)
Caracteristicas de las secciones cónicas
Una familia de secciones cónicas de excentricidad variable comparten un punto focal y una línea directriz, incluyendo una elipse (roja, e = 1/2 ), una parábola (verde, e = 1 ) y una hipérbola (azul, e = 2 ). La cónica de excentricidad 0 en esta figura es un círculo infinitesimal centrado en el foco, y la cónica de excentricidad ∞ es un par de líneas separadas infinitesimalmente.
Un círculo de radio finito tiene una directriz infinitamente distante, mientras que un par de líneas de separación finita tienen un foco infinitamente distante.

En matemáticas , la excentricidad de una sección cónica es un número real no negativo que caracteriza de forma única su forma.

Se puede pensar en la excentricidad como una medida de cuánto se desvía una sección cónica de ser circular. En particular:

  • La excentricidad de un círculo es 0.
  • La excentricidad de una elipse que no es un círculo está entre 0 y 1.
  • La excentricidad de una parábola es 1.
  • La excentricidad de una hipérbola es mayor que 1.
  • La excentricidad de un par de líneas es ∞ {\estilo de visualización\infty}

Dos secciones cónicas con la misma excentricidad son similares .

Definiciones

Sección plana de un cono

Cualquier sección cónica puede definirse como el lugar geométrico de los puntos cuyas distancias a un punto (el foco) y a una línea (la directriz) guardan una relación constante. Esa relación se denomina excentricidad, comúnmente denotada como e .

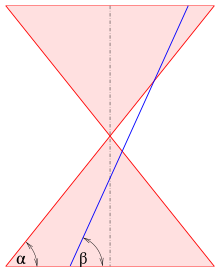
La excentricidad también se puede definir en términos de la intersección de un plano y un cono de doble filo asociado con la sección cónica. Si el cono está orientado con su eje vertical, la excentricidad es [1]

mi = pecado ⁡ β pecado ⁡ alfa ,     0 < alfa < 90 ∘ ,   0 ≤ β ≤ 90 ∘   , {\displaystyle e={\frac {\sin \beta }{\sin \alpha }},\ \ 0<\alpha <90^{\circ },\ 0\leq \beta \leq 90^{\circ }\ ,}

donde β es el ángulo entre el plano y la horizontal y α es el ángulo entre la generatriz de inclinación del cono y la horizontal. Para el plano la sección es un círculo, para una parábola. (El plano no debe encontrarse con el vértice del cono). β = 0 {\displaystyle \beta = 0} β = alfa {\displaystyle \beta =\alpha}

La excentricidad lineal de una elipse o hipérbola, denotada c (o a veces f o e ), es la distancia entre su centro y cualquiera de sus dos focos . La excentricidad puede definirse como la relación entre la excentricidad lineal y el semieje mayor a : es decir, (al carecer de un centro, la excentricidad lineal de las parábolas no está definida). Vale la pena señalar que una parábola puede tratarse como una elipse o una hipérbola, pero con un punto focal en el infinito . mi = do a {\displaystyle e={\frac {c}{a}}}

Nombres alternativos

La excentricidad a veces se denomina primera excentricidad para distinguirla de la segunda y la tercera excentricidad definidas para las elipses (ver más abajo). La excentricidad también se denomina a veces excentricidad numérica .

En el caso de elipses e hipérbolas, la excentricidad lineal a veces se denomina separación semifocal .

Notación

Se utilizan comúnmente tres convenciones de notación:

  1. e para la excentricidad y c para la excentricidad lineal.
  2. ε para la excentricidad y e para la excentricidad lineal.
  3. e o ϵ< para la excentricidad y f para la excentricidad lineal (mnemónico para separación semifocal ) .

Este artículo utiliza la primera notación.

Valores

Formulario estándar

Sección cónicaEcuaciónExcentricidad ( e )Excentricidad lineal ( c )
Círculo incógnita 2 + y 2 = a 2 {\displaystyle x^{2}+y^{2}=r^{2}} 0 {\displaystyle 0} 0 {\displaystyle 0}
Elipse x 2 a 2 + y 2 b 2 = 1 {\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1} o donde y 2 a 2 + x 2 b 2 = 1 {\displaystyle {\frac {y^{2}}{a^{2}}}+{\frac {x^{2}}{b^{2}}}=1} a > b {\displaystyle a>b} 1 − b 2 a 2 {\displaystyle {\sqrt {1-{\frac {b^{2}}{a^{2}}}}}} a 2 − b 2 {\displaystyle {\sqrt {a^{2}-b^{2}}}}
Parábola x 2 = 4 a y {\displaystyle x^{2}=4ay} 1 {\displaystyle 1} indefinido ( ) ∞ {\displaystyle \infty }
Hipérbola x 2 a 2 − y 2 b 2 = 1 {\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1} o y 2 a 2 − x 2 b 2 = 1 {\displaystyle {\frac {y^{2}}{a^{2}}}-{\frac {x^{2}}{b^{2}}}=1} 1 + b 2 a 2 {\displaystyle {\sqrt {1+{\frac {b^{2}}{a^{2}}}}}} a 2 + b 2 {\displaystyle {\sqrt {a^{2}+b^{2}}}}

Aquí, para la elipse y la hipérbola, a es la longitud del semieje mayor y b es la longitud del semieje menor.

Forma general

Cuando la sección cónica se da en la forma cuadrática general

A x 2 + B x y + C y 2 + D x + E y + F = 0 , {\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,}

La siguiente fórmula da la excentricidad e si la sección cónica no es una parábola (que tiene excentricidad igual a 1), ni una hipérbola degenerada ni una elipse degenerada , ni una elipse imaginaria: [2]

e = 2 ( A − C ) 2 + B 2 η ( A + C ) + ( A − C ) 2 + B 2 {\displaystyle e={\sqrt {\frac {2{\sqrt {(A-C)^{2}+B^{2}}}}{\eta (A+C)+{\sqrt {(A-C)^{2}+B^{2}}}}}}}

donde si el determinante de la matriz 3×3 η = 1 {\displaystyle \eta =1}

[ A B / 2 D / 2 B / 2 C E / 2 D / 2 E / 2 F ] {\displaystyle {\begin{bmatrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{bmatrix}}}

es negativo o si ese determinante es positivo. η = − 1 {\displaystyle \eta =-1}

Elipse e hipérbola con a constante y excentricidad cambiante e .

Elipses

La excentricidad de una elipse es estrictamente menor que 1. Cuando los círculos (que tienen excentricidad 0) se cuentan como elipses, la excentricidad de una elipse es mayor o igual a 0; si a los círculos se les da una categoría especial y se excluyen de la categoría de elipses, entonces la excentricidad de una elipse es estrictamente mayor que 0.

Para cualquier elipse, sea a la longitud de su semieje mayor y b la longitud de su semieje menor . En el sistema de coordenadas con origen en el centro de la elipse y eje x alineado con el eje mayor, los puntos de la elipse satisfacen la ecuación

x 2 a 2 + y 2 b 2 = 1 , {\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,}

con focos en coordenadas para ( ± c , 0 ) {\displaystyle (\pm c,0)} c = a 2 − b 2 . {\textstyle c={\sqrt {a^{2}-b^{2}}}.}

Definimos una serie de conceptos adicionales relacionados (sólo para elipses):

NombreSímboloen términos de a y ben términos de e
Primera excentricidad e {\displaystyle e} 1 − b 2 a 2 {\displaystyle {\sqrt {1-{\frac {b^{2}}{a^{2}}}}}} e {\displaystyle e}
Segunda excentricidad e ′ {\displaystyle e'} a 2 b 2 − 1 {\displaystyle {\sqrt {{\frac {a^{2}}{b^{2}}}-1}}} e 1 − e 2 {\displaystyle {\frac {e}{\sqrt {1-e^{2}}}}}
Tercera excentricidad e ″ = m {\displaystyle e''={\sqrt {m}}} a 2 − b 2 a 2 + b 2 {\displaystyle {\frac {\sqrt {a^{2}-b^{2}}}{\sqrt {a^{2}+b^{2}}}}} e 2 − e 2 {\displaystyle {\frac {e}{\sqrt {2-e^{2}}}}}
Excentricidad angular α {\displaystyle \alpha } cos − 1 ⁡ ( b a ) {\displaystyle \cos ^{-1}\left({\frac {b}{a}}\right)} sin − 1 ⁡ e {\displaystyle \sin ^{-1}e}

Otras fórmulas para la excentricidad de una elipse

La excentricidad de una elipse es, simplemente, la relación entre la excentricidad lineal c (distancia entre el centro de la elipse y cada foco) y la longitud del semieje mayor a .

e = c a . {\displaystyle e={\frac {c}{a}}.}

La excentricidad es también la relación entre el semieje mayor a y la distancia d del centro a la directriz:

e = a d . {\displaystyle e={\frac {a}{d}}.}

La excentricidad se puede expresar en términos del aplanamiento f (definido para el semieje mayor a y el semieje menor b ): f = 1 − b / a {\displaystyle f=1-b/a}

e = 1 − ( 1 − f ) 2 = f ( 2 − f ) . {\displaystyle e={\sqrt {1-(1-f)^{2}}}={\sqrt {f(2-f)}}.}

(El aplanamiento puede denotarse con g en algunas áreas temáticas si f es excentricidad lineal).

Defina los radios máximo y mínimo y como las distancias máxima y mínima desde cualquiera de los focos a la elipse (es decir, las distancias desde cualquiera de los focos a los dos extremos del eje mayor). Entonces, con semieje mayor a , la excentricidad está dada por r max {\displaystyle r_{\text{max}}} r min {\displaystyle r_{\text{min}}}

e = r max − r min r max + r min = r max − r min 2 a , {\displaystyle e={\frac {r_{\text{max}}-r_{\text{min}}}{r_{\text{max}}+r_{\text{min}}}}={\frac {r_{\text{max}}-r_{\text{min}}}{2a}},}

que es la distancia entre los focos dividida por la longitud del eje mayor.

Hipérbolas

La excentricidad de una hipérbola puede ser cualquier número real mayor que 1, sin límite superior. La excentricidad de una hipérbola rectangular es . 2 {\displaystyle {\sqrt {2}}}

Cuadrárica

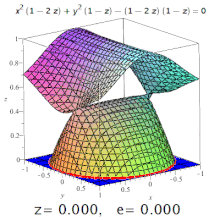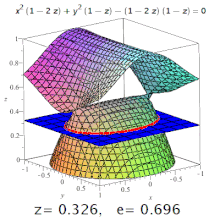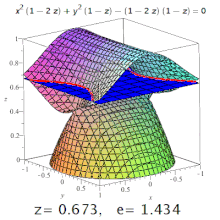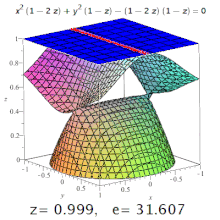
Elipses, hipérbolas con todas las excentricidades posibles desde cero hasta infinito y una parábola sobre una superficie cúbica.

La excentricidad de una cuadrática tridimensional es la excentricidad de una sección designada de la misma. Por ejemplo, en un elipsoide triaxial, la excentricidad meridional es la de la elipse formada por una sección que contiene tanto el eje más largo como el más corto (uno de los cuales será el eje polar), y la excentricidad ecuatorial es la excentricidad de la elipse formada por una sección que pasa por el centro, perpendicular al eje polar (es decir, en el plano ecuatorial). Pero: las secciones cónicas también pueden darse en superficies de orden superior (ver imagen).

Mecánica celeste

En mecánica celeste , para órbitas ligadas en un potencial esférico, la definición anterior se generaliza informalmente. Cuando la distancia del apocentro es cercana a la distancia del pericentro , se dice que la órbita tiene baja excentricidad; cuando son muy diferentes, se dice que la órbita es excéntrica o que tiene una excentricidad cercana a la unidad. Esta definición coincide con la definición matemática de excentricidad para elipses, en kepler, es decir, potenciales. 1 / r {\displaystyle 1/r}

Clasificaciones análogas

Varias clasificaciones en matemáticas utilizan terminología derivada de la clasificación de secciones cónicas por excentricidad:

Véase también

Referencias

  1. ^ Thomas, George B.; Finney, Ross L. (1979), Cálculo y geometría analítica (quinta edición), Addison-Wesley, pág. 434. ISBN  0-201-07540-7
  2. ^ Ayoub, Ayoub B., "La excentricidad de una sección cónica", The College Mathematics Journal 34(2), marzo de 2003, 116-121.
  3. ^ "Clasificación de ecuaciones diferenciales parciales lineales en dos variables independientes" . Consultado el 2 de julio de 2013 .
Wikimedia Commons tiene medios relacionados con Excentricidad .
  • MathWorld: Excentricidad
Retrieved from "https://en.wikipedia.org/w/index.php?title=Eccentricity_(mathematics)&oldid=1248081914"