Fuente de corriente de Widlar

Una fuente de corriente Widlar es una modificación del espejo de corriente básico de dos transistores que incorpora una resistencia de degeneración del emisor solo para el transistor de salida, lo que permite que la fuente de corriente genere corrientes bajas utilizando solo valores de resistencia moderados. ^{[1] [2] [3]}

El circuito de Widlar se puede utilizar con transistores bipolares , transistores MOS e incluso tubos de vacío . Un ejemplo de aplicación es el amplificador operacional 741 ^[4] , y Widlar utilizó el circuito como parte de muchos diseños. ^[5]

Este circuito lleva el nombre de su inventor, Bob Widlar , y fue patentado en 1967. ^{[6] [7]}

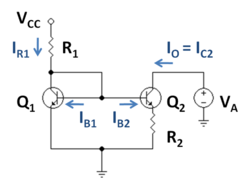
La figura 1 es un ejemplo de fuente de corriente Widlar que utiliza transistores bipolares, donde la resistencia del emisor R ₂ está conectada al transistor de salida Q ₂ y tiene el efecto de reducir la corriente en Q ₂ en relación con Q _1. La clave de este circuito es que la caída de voltaje a través de la resistencia R ₂ se resta del voltaje base-emisor del transistor Q ₂ , apagando así este transistor en comparación con el transistor Q ₁ . Esta observación se expresa igualando las expresiones de voltaje base que se encuentran en ambos lados del circuito en la figura 1 como:

${\displaystyle {\begin{aligned}&V_{\text{B}}=V_{\text{BE1}}=V_{\text{BE2}}+(\beta _{2}+1)I_{\text{B2}}R_{2}\\\Rightarrow {}&{\frac {1}{R_{2}}}\left(V_{\text{BE1}}-V_{\text{BE2}}\right)=(\beta _{2}+1)I_{\text{B2}}\ ,\end{aligned}}}$

donde β ₂ es el valor beta del transistor de salida, que no es el mismo que el del transistor de entrada, en parte porque las corrientes en los dos transistores son muy diferentes. ^[8] La variable I _B2 es la corriente de base del transistor de salida, V _BE se refiere al voltaje base-emisor. Esta ecuación implica (usando la ecuación del diodo Shockley ):

Ecuación 1

${\displaystyle {\begin{aligned}(\beta _{2}+1)I_{\text{B2}}&=\left(1+{\frac {1}{\beta _{2}}}\right)I_{\text{C2}}={\frac {1}{R_{2}}}\left(V_{\text{BE1}}-V_{\text{BE2}}\right)\\&={\frac {V_{\text{T}}}{R_{2}}}\left[\ln \left(I_{\text{C1}}/I_{\text{S1}}\right)-\ln \left(I_{\text{C2}}/I_{\text{S2}}\right)\right]={\frac {V_{\text{T}}}{R_{2}}}\ln \left({\frac {I_{\text{C1}}I_{\text{S2}}}{I_{\text{C2}}I_{\text{S1}}}}\right)\ ,\end{aligned}}}$

donde V _T es el voltaje térmico .

Esta ecuación permite la aproximación de que las corrientes son mucho mayores que las corrientes de escala , I _S1 e I _S2 ; una aproximación válida excepto para niveles de corriente cercanos al corte . En lo sucesivo, se supone que las corrientes de escala son idénticas; en la práctica, esto debe organizarse específicamente.

Para diseñar el espejo, la corriente de salida debe estar relacionada con los dos valores de resistencia R ₁ y R ₂ . Una observación básica es que el transistor de salida está en modo activo solo mientras su voltaje colector-base no sea cero. Por lo tanto, la condición de polarización más simple para el diseño del espejo establece el voltaje aplicado V _A para que sea igual al voltaje base V _B . Este valor útil mínimo de V _A se denomina voltaje de cumplimiento de la fuente de corriente. Con esa condición de polarización, el efecto Early no juega ningún papel en el diseño. ^[9]

Estas consideraciones sugieren el siguiente procedimiento de diseño:

• Seleccione la corriente de salida deseada, I _O = I _C2 .
• Seleccione la corriente de referencia, I _R1 , que se supone que es mayor que la corriente de salida, probablemente considerablemente mayor (ese es el propósito del circuito).
• Determinar la corriente del colector de entrada de Q ₁ , I _C1 :

  ${\displaystyle I_{\text{C1}}={\frac {\beta _{1}}{\beta _{1}+1}}\left(I_{\text{R1}}-{\frac {I_{\text{C2}}}{\beta _{2}}}\right)\ .}$

• Determinar el voltaje base V _BE1 utilizando la ley del diodo Shockley

  ${\displaystyle V_{\text{BE1}}=V_{\text{T}}\ln \left({\frac {I_{\text{C1}}}{I_{\text{S}}}}\right)=V_{\text{A}}\ .}$

donde IS es un parámetro del dispositivo a veces llamado corriente de _escala .

El valor del voltaje base también establece el voltaje de cumplimiento V _A = V _BE1 . Este voltaje es el voltaje más bajo para el cual el espejo funciona correctamente.

• Determinar R ₁ :

  ${\displaystyle R_{1}={\frac {V_{\text{CC}}-V_{\text{A}}}{I_{\text{R1}}}}\ .}$

• Determine la resistencia de la pata del emisor R ₂ utilizando la ecuación 1 (para reducir el desorden, las corrientes de escala se eligen iguales):

  ${\displaystyle R_{2}={\frac {V_{\text{T}}}{\left(1+{\frac {1}{\beta _{2}}}\right)I_{\text{C2}}}}\ln \left({\frac {I_{\text{C1}}}{I_{\text{C2}}}}\right)\ .}$

El problema inverso del diseño es encontrar la corriente cuando se conocen los valores de las resistencias. A continuación se describe un método iterativo. Suponga que la fuente de corriente está polarizada, de modo que el voltaje colector-base del transistor de salida Q ₂ es cero. La corriente a través de R ₁ es la corriente de entrada o de referencia dada como,

${\displaystyle {\begin{aligned}I_{\text{R1}}&=I_{\text{C1}}+I_{\text{B1}}+I_{\text{B2}}\\&=I_{\text{C1}}+{\frac {I_{\text{C1}}}{\beta _{1}}}+{\frac {I_{\text{C2}}}{\beta _{2}}}\\&={\frac {1}{R_{1}}}\left(V_{\text{CC}}-V_{\text{BE1}}\right)\end{aligned}}}$

Reordenando, I _C1 se encuentra como:

Ecuación 2

${\displaystyle I_{\text{C1}}={\frac {\beta _{1}}{\beta _{1}+1}}\left({\frac {V_{\text{CC}}-V_{\text{BE1}}}{R_{1}}}-{\frac {I_{\text{C2}}}{\beta _{2}}}\right)}$

La ecuación del diodo proporciona:

Ecuación 3

${\displaystyle V_{\text{BE1}}=V_{\text{T}}\ln \left({\frac {I_{\text{C1}}}{I_{\text{S1}}}}\right)\ .}$

La ecuación 1 proporciona:

${\displaystyle I_{\text{C2}}={\frac {V_{\text{T}}}{\left(1+{\frac {1}{\beta _{2}}}\right)R_{2}}}\ln \left({\frac {I_{\text{C1}}}{I_{\text{C2}}}}\right)\ .}$

Estas tres relaciones son una determinación implícita no lineal para las corrientes que se pueden resolver mediante iteración.

• Suponemos valores iniciales para I _C1 y I _C2 .
• Encontramos un valor para V _BE1 :

  ${\displaystyle V_{\text{BE1}}=V_{\text{T}}\ln \left({\frac {I_{\text{C1}}}{I_{\text{S1}}}}\right)\ .}$

• Encontramos un nuevo valor para I _C1 :

  ${\displaystyle I_{\text{C1}}={\frac {\beta _{1}}{\beta _{1}+1}}\left({\frac {V_{\text{CC}}-V_{\text{BE1}}}{R_{1}}}-{\frac {I_{\text{C2}}}{\beta _{2}}}\right)}$

• Encontramos un nuevo valor para I _C2 :

  ${\displaystyle I_{\text{C2}}={\frac {V_{\text{T}}}{\left(1+{\frac {1}{\beta _{2}}}\right)R_{2}}}\ln \left({\frac {I_{\text{C1}}}{I_{\text{C2}}}}\right)\ .}$

Este procedimiento se repite hasta la convergencia y se configura de forma práctica en una hoja de cálculo. Basta con utilizar una macro para copiar los nuevos valores en las celdas de la hoja de cálculo que contienen los valores iniciales para obtener la solución en poco tiempo.

Tenga en cuenta que con el circuito que se muestra, si V _CC cambia, la corriente de salida cambiará. Por lo tanto, para mantener la corriente de salida constante a pesar de las fluctuaciones en V _CC , el circuito debe ser accionado por una fuente de corriente constante en lugar de usar la resistencia R ₁ .

Las ecuaciones trascendentales anteriores se pueden resolver exactamente en términos de la función W de Lambert .

Una propiedad importante de una fuente de corriente es su pequeña impedancia de salida incremental de señal, que idealmente debería ser infinita. El circuito de Widlar introduce retroalimentación de corriente local para el transistor . Cualquier aumento en la corriente en Q ₂ aumenta la caída de voltaje a través de R ₂ , reduciendo el V _BE para Q ₂ , contrarrestando así el aumento de corriente. Esta retroalimentación significa que la impedancia de salida del circuito aumenta, porque la retroalimentación que involucra a R ₂ fuerza el uso de un voltaje mayor para impulsar una corriente dada.${\displaystyle \scriptstyle Q_{2}}$

La resistencia de salida se encuentra utilizando un modelo de pequeña señal para el circuito, que se muestra en la Figura 2. El transistor Q ₁ se reemplaza por su resistencia de emisor de pequeña señal r _E porque está conectado a un diodo. ^[10] El transistor Q ₂ se reemplaza con su modelo híbrido-pi . Se aplica una corriente de prueba I _{x en la salida.}

Utilizando la figura, la resistencia de salida se determina utilizando las leyes de Kirchhoff. Utilizando la ley de voltaje de Kirchhoff desde la tierra de la izquierda hasta la conexión a tierra de R ₂ :

${\displaystyle I_{\text{b}}\left[(R_{1}\parallel r_{\text{E}})+r_{\pi }\right]+[I_{\text{x}}+I_{\text{b}}]R_{2}=0\ .}$

Reorganizando:

${\displaystyle I_{\text{b}}=-I_{\text{x}}{\frac {R_{2}}{(R_{1}\parallel r_{\text{E}})+r_{\pi }+R_{2}}}\ .}$

Utilizando la ley de voltaje de Kirchhoff desde la conexión a tierra de R ₂ a la tierra de la corriente de prueba:

${\displaystyle V_{\text{x}}=I_{\text{x}}(R_{2}+r_{\text{O}})+I_{\text{b}}(R_{2}-\beta r_{\text{O}})\ ,}$

o, sustituyendo por I _b :

Ecuación 4

${\displaystyle R_{\text{O}}={\frac {V_{\text{x}}}{I_{\text{x}}}}=r_{\text{O}}\left[1+{\frac {\beta R_{2}}{(R_{1}\parallel r_{\text{E}})+r_{\pi }+R_{2}}}\right]}$ ${\displaystyle +\ R_{2}\left[{\frac {(R_{1}\parallel r_{\text{E}})+r_{\pi }}{(R_{1}\parallel r_{\text{E}})+r_{\pi }+R_{2}}}\right]\ .}$

Según la ecuación 4 , la resistencia de salida de la fuente de corriente de Widlar aumenta con respecto a la del propio transistor de salida (que es r _O ) siempre que R ₂ sea lo suficientemente grande en comparación con el r _π del transistor de salida (las resistencias grandes R ₂ hacen que el factor que multiplica r _O se acerque al valor ( β + 1)). El transistor de salida transporta una corriente baja, lo que hace que r _π sea grande, y el aumento de R ₂ tiende a reducir aún más esta corriente, lo que provoca un aumento correlacionado de r _π . Por lo tanto, un objetivo de R ₂ ≫ r _π puede ser poco realista y se proporciona una discusión más detallada a continuación. La resistencia R ₁ ∥ r _E generalmente es pequeña porque la resistencia del emisor r _E generalmente es de solo unos pocos ohmios.

La dependencia actual de las resistencias r _π y r _O se analiza en el artículo Modelo híbrido-pi . La dependencia actual de los valores de las resistencias es:

${\displaystyle r_{\pi }={\frac {v_{\text{be}}}{i_{\text{b}}}}{\Bigg |}_{v_{\text{ce}}=0}={\frac {V_{\text{T}}}{I_{\text{B2}}}}=\beta _{2}{\frac {V_{\text{T}}}{I_{\text{C2}}}}\ ,}$

y

${\displaystyle r_{\text{O}}={\frac {v_{\text{ce}}}{i_{\text{c}}}}{\Bigg |}_{v_{\text{be}}=0}={\frac {V_{\text{A}}}{I_{\text{C2}}}}}$

es la resistencia de salida debido al efecto Early cuando V _CB = 0 V (el parámetro del dispositivo V _A es el voltaje Early).

De antes en este artículo (estableciendo las corrientes de escala iguales para mayor comodidad):Ecuación 5

${\displaystyle R_{2}={\frac {V_{\text{T}}}{\left(1+{\frac {1}{\beta _{2}}}\right)I_{\text{C2}}}}\ln \left({\frac {I_{\text{C1}}}{I_{\text{C2}}}}\right)\ .}$

En consecuencia, para el caso habitual de r _E pequeño , y descuidando el segundo término en R _O con la expectativa de que el término principal que involucra a r _O sea mucho más grande:Ecuación 6

${\displaystyle {\begin{aligned}R_{\text{O}}&\approx r_{\text{O}}\left(1+{\frac {\beta _{2}R_{2}}{r_{\pi }+R_{2}}}\right)\\&=r_{\text{O}}\left(1+{\frac {\beta _{2}\ln \left({\frac {I_{\text{C1}}}{I_{\text{C2}}}}\right)}{\beta _{2}+1+\ln \left({\frac {I_{\text{C1}}}{I_{\text{C2}}}}\right)}}\right)\end{aligned}}}$

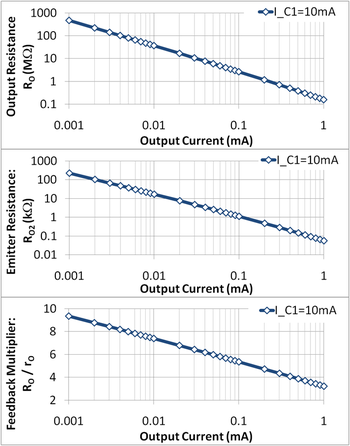
donde la última forma se encuentra sustituyendo la ecuación 5 por R ₂ . La ecuación 6 muestra que un valor de resistencia de salida mucho mayor que r _O del transistor de salida resulta solo para diseños con I _C1 >> I _C2 . La figura 3 muestra que la resistencia de salida del circuito R _O no está determinada tanto por la retroalimentación como por la dependencia de la corriente de la resistencia r _O del transistor de salida (la resistencia de salida en la figura 3 varía cuatro órdenes de magnitud, mientras que el factor de retroalimentación varía solo en un orden de magnitud).

El aumento de I _C1 para aumentar el factor de retroalimentación también da como resultado un aumento de la tensión de cumplimiento, lo que no es bueno, ya que significa que la fuente de corriente opera en un rango de tensión más restringido. Por ejemplo, con un objetivo de tensión de cumplimiento establecido, colocando un límite superior en I _C1 y con un objetivo de resistencia de salida que se debe cumplir, el valor máximo de la corriente de salida I _C2 es limitado.

El panel central de la Figura 3 muestra la compensación de diseño entre la resistencia de la pata del emisor y la corriente de salida: una corriente de salida más baja requiere una resistencia de pata más grande y, por lo tanto, un área más grande para el diseño. Por lo tanto, un límite superior del área establece un límite inferior para la corriente de salida y un límite superior para la resistencia de salida del circuito.

La ecuación 6 para R _O depende de la selección de un valor de R ₂ según la ecuación 5. Esto significa que la ecuación 6 no es una fórmula de comportamiento del circuito , sino una ecuación de valor de diseño . Una vez que se selecciona R _{2 para un objetivo de diseño particular utilizando} la ecuación 5 , a partir de entonces su valor se fija. Si la operación del circuito hace que las corrientes, voltajes o temperaturas se desvíen de los valores diseñados, entonces para predecir los cambios en R _O causados ​​por dichas desviaciones, se debe utilizar la ecuación 4 , no la ecuación 6 .

• Fuente actual
• Espejo actual
• Fuente de corriente de Wilson

• Linden T. Harrison (2005). Referencias de fuentes de corriente y voltaje: una referencia de diseño para ingenieros electrónicos. Elsevier-Newnes. ISBN 0-7506-7752-X.
• Sundaram Natarajan (2005). Microelectrónica: análisis y diseño. Tata McGraw-Hill. pág. 319. ISBN 0-07-059096-6.
• Espejos actuales y cargas activas: Mu-Huo Cheng