Cálculo de escala temporal

En matemáticas , el cálculo a escala temporal es una unificación de la teoría de ecuaciones diferenciales con la de ecuaciones diferenciales , unificando el cálculo integral y diferencial con el cálculo de diferencias finitas , ofreciendo un formalismo para estudiar sistemas híbridos . Tiene aplicaciones en cualquier campo que requiera modelado simultáneo de datos discretos y continuos. Da una nueva definición de derivada tal que si uno diferencia una función definida en los números reales entonces la definición es equivalente a la diferenciación estándar, pero si uno usa una función definida en los números enteros entonces es equivalente al operador de diferencia hacia adelante .

El cálculo a escala de tiempo fue introducido en 1988 por el matemático alemán Stefan Hilger. ^[1] Sin embargo, se han utilizado ideas similares antes y se remontan al menos a la introducción de la integral de Riemann-Stieltjes , que unifica sumas e integrales.

Muchos resultados relativos a ecuaciones diferenciales se trasladan con bastante facilidad a los resultados correspondientes para ecuaciones de diferencia, mientras que otros resultados parecen ser completamente diferentes de sus contrapartes continuas . ^[2] El estudio de ecuaciones dinámicas en escalas de tiempo revela tales discrepancias y ayuda a evitar demostrar los resultados dos veces: una para ecuaciones diferenciales y otra para ecuaciones de diferencia. La idea general es demostrar un resultado para una ecuación dinámica donde el dominio de la función desconocida es una denominada escala de tiempo (también conocida como conjunto de tiempo), que puede ser un subconjunto cerrado arbitrario de los números reales. De esta manera, los resultados se aplican no solo al conjunto de números reales o al conjunto de números enteros , sino a escalas de tiempo más generales, como un conjunto de Cantor .

Los tres ejemplos más populares de cálculo en escalas de tiempo son el cálculo diferencial , el cálculo de diferencias y el cálculo cuántico . Las ecuaciones dinámicas en una escala de tiempo tienen potencial para aplicaciones como la dinámica de poblaciones . Por ejemplo, pueden modelar poblaciones de insectos que evolucionan continuamente durante la temporada, mueren en invierno mientras sus huevos están incubando o en estado latente y luego eclosionan en una nueva temporada, dando lugar a una población que no se superpone.

Una escala de tiempo (o cadena de medida ) es un subconjunto cerrado de la línea real . La notación común para una escala de tiempo general es .${\displaystyle \mathbb {R}}$${\displaystyle \mathbb {T}}$

Los dos ejemplos de escalas de tiempo más comunes son los números reales y la escala de tiempo discreta .${\displaystyle \mathbb {R}}$${\displaystyle h\mathbb {Z}}$

Un solo punto en una escala de tiempo se define como:

${\displaystyle t:t\in \mathbb {T}}$

Los operadores de salto hacia adelante y salto hacia atrás representan el punto más cercano en la escala de tiempo a la derecha y a la izquierda de un punto dado , respectivamente. Formalmente:${\estilo de visualización t}$

${\displaystyle \sigma(t)=\inf\{s\in \mathbb {T} :s>t\}}$(operador de cambio/salto hacia adelante)

${\displaystyle \rho (t)=\sup\{s\in \mathbb {T} :s<t\}}$(operador de salto/desplazamiento hacia atrás)

La granulosidad es la distancia desde un punto hasta el punto más cercano a la derecha y viene dada por:${\displaystyle \mu }$

${\displaystyle \mu (t)=\sigma (t)-t.}$

Para un denso a la derecha , y . Para un denso a la izquierda ,${\displaystyle t}$${\displaystyle \sigma (t)=t}$${\displaystyle \mu (t)=0}$
${\displaystyle t}$${\displaystyle \rho (t)=t.}$

Para cualquier , es:${\displaystyle t\in \mathbb {T} }$${\displaystyle t}$

• queda denso si${\displaystyle \rho (t)=t}$
• derecho denso si${\displaystyle \sigma (t)=t}$
• se dejó disperso si${\displaystyle \rho (t)<t}$
• derecho disperso si${\displaystyle \sigma (t)>t}$
• denso si tanto la izquierda como la derecha son densas
• aislado si tanto la izquierda como la derecha están dispersas

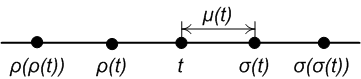
Como lo ilustra la figura de la derecha:

• El punto es denso${\displaystyle t_{1}}$
• El punto está a la izquierda denso y a la derecha disperso.${\displaystyle t_{2}}$
• El punto está aislado${\displaystyle t_{3}}$
• El punto está a la izquierda disperso y a la derecha denso.${\displaystyle t_{4}}$

La continuidad de una escala de tiempo se redefine como equivalente a la densidad. Se dice que una escala de tiempo es continua por la derecha en el punto${\displaystyle t}$ si es densa por la derecha en el punto . De manera similar, se dice que una escala de tiempo es continua por la izquierda en el punto si es densa por la izquierda en el punto .${\displaystyle t}$${\displaystyle t}$${\displaystyle t}$

Tome una función:

${\displaystyle f:\mathbb {T} \to \mathbb {R} ,}$

(donde R podría ser cualquier espacio de Banach , pero se establece en la línea real para simplificar).

Definición: La derivada delta (también derivada de Hilger) existe si y sólo si:${\displaystyle f^{\Delta }(t)}$

Para cada existe un vecindario de tal que:${\displaystyle \varepsilon >0}$${\displaystyle U}$${\displaystyle t}$

${\displaystyle \left|f(\sigma (t))-f(s)-f^{\Delta }(t)(\sigma (t)-s)\right|\leq \varepsilon \left|\sigma (t)-s\right|}$

Para todos en .${\displaystyle s}$${\displaystyle U}$

Tome entonces , , ; es la derivada utilizada en el cálculo estándar . Si (los enteros ), , , es el operador de diferencia hacia adelante utilizado en ecuaciones diferenciales.${\displaystyle \mathbb {T} =\mathbb {R} .}$${\displaystyle \sigma (t)=t}$${\displaystyle \mu (t)=0}$${\displaystyle f^{\Delta }=f'}$${\displaystyle \mathbb {T} =\mathbb {Z} }$${\displaystyle \sigma (t)=t+1}$${\displaystyle \mu (t)=1}$${\displaystyle f^{\Delta }=\Delta f}$

La integral delta se define como la antiderivada con respecto a la derivada delta. Si tiene una derivada continua, se establece${\displaystyle F(t)}$${\displaystyle f(t)=F^{\Delta }(t)}$

${\displaystyle \int _{r}^{s}f(t)\Delta (t)=F(s)-F(r).}$

Se puede definir una transformada de Laplace para funciones en escalas de tiempo, que utiliza la misma tabla de transformadas para cualquier escala de tiempo arbitraria. Esta transformada se puede utilizar para resolver ecuaciones dinámicas en escalas de tiempo. Si la escala de tiempo son los números enteros no negativos, entonces la transformada es igual ^[2] a una transformada Z modificada :$${\displaystyle {\mathcal {Z}}'\{x[z]\}={\frac {{\mathcal {Z}}\{x[z+1]\}}{z+1}}}$$

Las ecuaciones diferenciales parciales y las ecuaciones en diferencias parciales se unifican como ecuaciones dinámicas parciales en escalas de tiempo. ^{[3] [4] [5]}

La integración múltiple en escalas de tiempo se trata en Bohner (2005). ^[6]

Las ecuaciones diferenciales estocásticas y las ecuaciones de diferencias estocásticas se pueden generalizar a ecuaciones dinámicas estocásticas en escalas de tiempo. ^[7]

Asociada a cada escala de tiempo hay una medida natural ^{[8] [9]} definida mediante

${\displaystyle \mu ^{\Delta }(A)=\lambda (\rho ^{-1}(A)),}$

donde denota la medida de Lebesgue y es el operador de desplazamiento hacia atrás definido en . La integral delta resulta ser la integral de Lebesgue-Stieltjes habitual con respecto a esta medida${\displaystyle \lambda }$${\displaystyle \rho }$${\displaystyle \mathbb {R} }$

${\displaystyle \int _{r}^{s}f(t)\Delta t=\int _{[r,s)}f(t)d\mu ^{\Delta }(t)}$

y la derivada delta resulta ser la derivada de Radon-Nikodym con respecto a esta medida ^[10]

${\displaystyle f^{\Delta }(t)={\frac {df}{d\mu ^{\Delta }}}(t).}$

El delta de Dirac y el delta de Kronecker se unifican en escalas de tiempo como el delta de Hilger : ^{[11] [12]}

${\displaystyle \delta _{a}^{\mathbb {H} }(t)={\begin{cases}{\dfrac {1}{\mu (a)}},&t=a\\0,&t\neq a\end{cases}}}$

El cálculo fraccional en escalas de tiempo se trata en Bastos, Mozyrska y Torres. ^[13]

• Análisis de fractales para ecuaciones dinámicas en un conjunto de Cantor .
• Análisis de múltiples escalas
• Método de promediar
• Método de promediado de Krylov-Bogoliubov

• Agarwal, Ravi; Bohner, Martin; O'Regan, Donal; Peterson, Allan (2002). "Ecuaciones dinámicas en escalas de tiempo: un estudio". Revista de Matemática Computacional y Aplicada . 141 (1–2): 1–26. Bibcode :2002JCoAM.141....1A. doi : 10.1016/S0377-0427(01)00432-0 .
• Ecuaciones dinámicas en escalas de tiempo Número especial de Journal of Computational and Applied Mathematics (2002)
• Ecuaciones dinámicas y aplicaciones Número especial de Advances in Difference Equations (2006)
• Ecuaciones dinámicas en escalas de tiempo: análisis cualitativo y aplicaciones Número especial de Nonlinear Dynamics And Systems Theory (2009)

• El grupo de escalas de tiempo de la Universidad de Baylor
• Escala de tiempowiki.org