Grupos de puntos en tres dimensiones
 Simetría involutiva C s , (*) [ ] =  |  Simetría cíclica C nv , (*nn) [n] =    |  Simetría diedro D nh , (*n22) [n,2] =      | |
| Grupo poliédrico , [n,3], (*n32) | |||
|---|---|---|---|
 Simetría tetraédrica T d , (*332) [3,3] =      |  Simetría octaédrica O h , (*432) [4,3] =      |  Simetría icosaédrica I h , (*532) [5,3] =      | |
Este artículo necesita ser editado para cumplir con el Manual de estilo de Wikipedia . En particular, tiene problemas con MOS:MATHSPECIAL - Use <math>... \setminus ...</math>or <math>... \smallsetminus ...</math>en lugar de U+2216 ∖ SET MINUS orU+005C \ SOLIDUS INVERSO para resta de conjuntos. ( febrero de 2024 ) |
En geometría , un grupo de puntos en tres dimensiones es un grupo de isometría en tres dimensiones que deja fijo el origen, o correspondientemente, un grupo de isometría de una esfera . Es un subgrupo del grupo ortogonal O(3), el grupo de todas las isometrías que dejan fijo el origen, o correspondientemente, el grupo de matrices ortogonales . O(3) a su vez es un subgrupo del grupo euclidiano E(3) de todas las isometrías.
Los grupos de simetría de objetos geométricos son grupos de isometría. Por consiguiente, el análisis de los grupos de isometría es un análisis de posibles simetrías . Todas las isometrías de un objeto 3D acotado (finito) tienen uno o más puntos fijos comunes. Seguimos la convención habitual eligiendo el origen como uno de ellos.
El grupo de simetría de un objeto a veces también se denomina su grupo de simetría completo , en oposición a su grupo de simetría propio , la intersección de su grupo de simetría completo con E + (3) , que consiste en todas las isometrías directas , es decir, isometrías que preservan la orientación . Para un objeto acotado, el grupo de simetría propio se denomina su grupo de rotación . Es la intersección de su grupo de simetría completo con SO(3) , el grupo de rotación completo del espacio 3D. El grupo de rotación de un objeto acotado es igual a su grupo de simetría completo si y solo si el objeto es quiral .
Los grupos de puntos que se generan puramente mediante un conjunto finito de planos de reflexión que pasan por el mismo punto son los grupos de Coxeter finitos , representados por la notación de Coxeter .
Los grupos puntuales en tres dimensiones son muy utilizados en química , especialmente para describir las simetrías de una molécula y de los orbitales moleculares que forman enlaces covalentes , y en este contexto también se denominan grupos puntuales moleculares .
Isometrías 3D que dejan el origen fijo
Las operaciones de grupo de simetría ( symmetry operations ) son las isometrías del espacio tridimensional R 3 que dejan fijo el origen, formando el grupo O(3). Estas operaciones se pueden categorizar como:
- Las operaciones de simetría directa (que preservan la orientación), que forman el grupo SO(3):
- La operación identidad, denotada por E o la matriz identidad I.
- Rotación sobre un eje que pasa por el origen en un ángulo θ. La rotación en θ = 360°/ n para cualquier entero positivo n se denota C n (de la notación de Schoenflies para el grupo C n que genera ). La operación de identidad, también escrita C 1 , es un caso especial del operador de rotación.
- Las operaciones indirectas (de inversión de orientación):
- Inversión, denotada por i o C i , es decir, rotación de 180° sobre un eje de coordenadas seguida de una reflexión en el plano de coordenadas ortogonal. La notación matricial es −I .
- Reflexión en un plano que pasa por el origen, denotado σ.
- Rotación impropia , también llamada rotación-reflexión: rotación sobre un eje en un ángulo θ, combinada con reflexión en el plano que pasa por el origen perpendicular al eje. La rotación-reflexión en θ = 360°/ n para cualquier entero positivo n se denota S n (de la notación de Schoenflies para el grupo S n que genera si n es par).
La inversión es un caso especial de rotación-reflexión (i = S 2 ), al igual que la reflexión (σ = S 1 ), por lo que estas operaciones a menudo se consideran rotaciones impropias.
A veces se añade un circunflejo al símbolo para indicar un operador, como en Ĉ n y Ŝ n .
Conjugación
Al comparar el tipo de simetría de dos objetos, el origen se elige para cada uno por separado, es decir, no es necesario que tengan el mismo centro. Además, se considera que dos objetos son del mismo tipo de simetría si sus grupos de simetría son subgrupos conjugados de O(3) (dos subgrupos H 1 , H 2 de un grupo G son conjugados , si existe g ∈ G tal que H 1 = g −1 H 2 g ).
Por ejemplo, dos objetos 3D tienen el mismo tipo de simetría:
- si ambos tienen simetría especular, pero con respecto a un plano especular diferente
- si ambos tienen simetría rotacional triple, pero con respecto a un eje diferente.
En el caso de múltiples planos especulares y/o ejes de rotación, dos grupos de simetría son del mismo tipo de simetría si y solo si hay una rotación que mapea toda la estructura del primer grupo de simetría a la del segundo. (De hecho, habrá más de una rotación de este tipo, pero no un número infinito como cuando hay solo un espejo o eje). La definición de conjugación también permitiría una imagen especular de la estructura, pero esto no es necesario, la estructura en sí es aquiral. Por ejemplo, si un grupo de simetría contiene un eje de rotación triple, contiene rotaciones en dos direcciones opuestas. (La estructura es quiral para 11 pares de grupos espaciales con un eje helicoidal).
Grupos de isometría infinitos
Existen muchos grupos de isometría infinitos ; por ejemplo, el " grupo cíclico " (que significa que es generado por un elemento, no debe confundirse con un grupo de torsión ) generado por una rotación de un número irracional de vueltas alrededor de un eje. Podemos crear grupos abelianos no cíclicos agregando más rotaciones alrededor del mismo eje. El conjunto de puntos en un círculo a números racionales de grados alrededor del círculo ilustra un grupo de puntos que requiere un número infinito de generadores . También existen grupos no abelianos generados por rotaciones alrededor de diferentes ejes. Estos suelen ser grupos libres (genéricamente) . Serán infinitos a menos que las rotaciones se elijan especialmente.
Todos los grupos infinitos mencionados hasta ahora no son cerrados como subgrupos topológicos de O(3). Ahora analizaremos los subgrupos topológicamente cerrados de O(3).

El grupo de simetría de la simetría esférica es O(3) ; SO(3) es el grupo de rotación correspondiente. Los otros grupos de isometría infinitos consisten en todas las rotaciones alrededor de un eje que pasa por el origen, y aquellas con reflexión adicional en los planos que pasan por el eje, y/o reflexión en el plano que pasa por el origen, perpendicular al eje. Aquellos con reflexión en los planos que pasan por el eje, con o sin reflexión en el plano que pasa por el origen perpendicular al eje, son los grupos de simetría para los dos tipos de simetría cilíndrica . Cualquier forma 3D (subconjunto de R 3 ) que tenga simetría rotacional infinita también debe tener simetría especular para cada plano que pase por el eje. Los objetos físicos que tienen simetría rotacional infinita también tendrán la simetría de los planos especulares que pasan por el eje, pero los campos vectoriales pueden no tenerla, por ejemplo, los vectores de velocidad de un cono que gira alrededor de su eje, o el campo magnético que rodea un cable. [1]
Existen siete grupos continuos que, en cierto sentido, son todos ellos límites de los grupos de isometría finitos. Estos llamados grupos puntuales límite o grupos límite de Curie reciben su nombre de Pierre Curie, que fue el primero en investigarlos. [1] [2] Las siete series infinitas de grupos axiales dan lugar a cinco grupos límite (dos de ellos son duplicados), y los siete grupos puntuales restantes producen dos grupos continuos más. En notación internacional, la lista es ∞, ∞2, ∞/m, ∞mm, ∞/mm, ∞∞ y ∞∞m. [3] No todos estos son posibles para los objetos físicos; por ejemplo, los objetos con simetría ∞∞ también tienen simetría ∞∞m. Véase a continuación otras designaciones y más detalles.
Grupos de isometría finitos
Las simetrías en 3D que dejan el origen fijo se caracterizan completamente por simetrías en una esfera centrada en el origen. Para grupos de puntos finitos en 3D, véase también grupos de simetría esférica .
Hasta la conjugación, el conjunto de grupos de puntos finitos 3D consta de:
- § Las siete series infinitas de grupos axiales, que tienen como máximo un eje de rotación de más de dos ejes; son los grupos de simetría finitos sobre un cilindro infinito , o equivalentemente, los de un cilindro finito. A veces se les llama grupos puntuales axiales o prismáticos.
- § Los siete grupos de puntos restantes, que tienen múltiples ejes de rotación de 3 o más pliegues; estos grupos también pueden caracterizarse como grupos de puntos que tienen múltiples ejes de rotación de 3 pliegues. Las combinaciones posibles son:
- Cuatro ejes triples (las tres simetrías tetraédricas T , T h y T d )
- Cuatro ejes triples y tres ejes cuádruples ( simetrías octaédricas O y Oh )
- Diez ejes triples y seis ejes quíntuples ( simetrías icosaédricas I e I h )
Según el teorema de restricción cristalográfico , sólo un número limitado de grupos puntuales son compatibles con la simetría traslacional discreta : 27 de las 7 series infinitas y 5 de las otras 7. En conjunto, estos forman los 32 denominados grupos puntuales cristalográficos .
Las siete series infinitas de grupos axiales
Las series infinitas de grupos axiales o prismáticos tienen un índice n , que puede ser cualquier entero; en cada serie, el n -ésimo grupo de simetría contiene n -veces de simetría rotacional alrededor de un eje, es decir, simetría con respecto a una rotación de un ángulo 360°/ n . n = 1 cubre los casos de ninguna simetría rotacional en absoluto. Hay cuatro series sin otros ejes de simetría rotacional (ver simetrías cíclicas ) y tres con ejes adicionales de simetría doble (ver simetría diedral ). Pueden entenderse como grupos puntuales en dos dimensiones extendidos con una coordenada axial y reflexiones en ella. Están relacionados con los grupos de frisos ; [4] pueden interpretarse como patrones de grupos de frisos repetidos n veces alrededor de un cilindro.
La siguiente tabla enumera varias notaciones para grupos puntuales: notación de Hermann-Mauguin (usada en cristalografía ), notación de Schönflies (usada para describir la simetría molecular ), notación orbifold y notación de Coxeter . Las últimas tres no solo están relacionadas convenientemente con sus propiedades, sino también con el orden del grupo. La notación orbifold es una notación unificada, también aplicable para grupos de papel tapiz y grupos de frisos . Los grupos cristalográficos tienen n restringido a 1, 2, 3, 4 y 6; eliminar la restricción cristalográfica permite cualquier número entero positivo. Las series son:
| Internacional | Moscas Schoen | Plegado orbi | Coxeter | Friso | Estructura. | Orden | Ejemplo | Comentarios | |
|---|---|---|---|---|---|---|---|---|---|
| Incluso n | N impar | (cilindro) | |||||||
| norte | C n | nn | [n] +   | pág. 1 | Zn | norte |  | Simetría rotacional de n pliegues | |
| 2 n | norte | S 2 n | n × | [2n + , 2 + ]      | pág. 11g | Z2n | 2 n |  | Simetría de reflexión rotatoria de 2 n pliegues |
| m /n | 2 n | Cnh | a * | [n + ,2]     | p11m | Zn × Z2 | 2 n |  | |
| En milímetros | nuevo | Cnv | * nn | [ n ]   | p1m1 | Dih n | 2 n |  | Simetría piramidal ; en biología, simetría birradial |
| número 22 | número 2 | Dn | 22 n | [ n ,2] +     | pág. 211 | Dih n | 2 n |  | Simetría diedral |
| 2 y 2 m | nuevo | D y d | 2* n | [2n , 2 + ]      | p2mg | Dih 2 n | 4 n |  | Simetría antiprismática |
| n /mmm | 2 y 2 m | D y H | *22 en | [ n ,2]     | p2mm | Dih n ×Z 2 | 4 n |  | Simetría prismática |
Para n impar tenemos Z 2 n = Z n × Z 2 y Dih 2 n = Dih n × Z 2 .
Los grupos C n (incluido el trivial C 1 ) y D n son quirales, los demás son aquirales.
Los términos horizontal (h) y vertical (v), y los subíndices correspondientes, se refieren al plano de espejo adicional, que puede ser paralelo al eje de rotación (vertical) o perpendicular al eje de rotación (horizontal).
Los grupos axiales no triviales más simples son equivalentes al grupo abstracto Z 2 :
- C i (equivalente a S 2 ) – simetría de inversión
- C 2 – simetría rotacional doble
- C s (equivalente a C 1h y C 1v ) – simetría de reflexión , también llamada simetría bilateral .

El segundo de ellos es el primero de los grupos uniaxiales ( grupos cíclicos ) C n de orden n (también aplicable en 2D), que se generan por una única rotación de ángulo 360°/ n . Además de esto, se puede añadir un plano de simetría perpendicular al eje, dando el grupo C n h de orden 2 n , o un conjunto de n planos de simetría que contienen el eje, dando el grupo C n v , también de orden 2 n . Este último es el grupo de simetría para una pirámide regular de n lados . Un objeto típico con grupo de simetría C n o D n es una hélice .
Si se suman los planos de reflexión horizontales y verticales, sus intersecciones dan n ejes de rotación de 180°, por lo que el grupo ya no es uniaxial. Este nuevo grupo de orden 4 n se llama D n h . Su subgrupo de rotaciones es el grupo diedro D n de orden 2 n , que todavía tiene los ejes de rotación dobles perpendiculares al eje de rotación primario, pero no tiene planos de simetría.
Nota: en 2D, D n incluye reflexiones, que también pueden verse como dar vuelta objetos planos sin distinción entre el lado frontal y el posterior; pero en 3D, las dos operaciones se distinguen: D n contiene "dar vuelta", no reflexiones.
Hay un grupo más en esta familia, llamado D n d (o D n v ), que tiene planos de simetría verticales que contienen el eje de rotación principal, pero en lugar de tener un plano de simetría horizontal, tiene una isometría que combina una reflexión en el plano horizontal y una rotación en un ángulo de 180°/ n . D n h es el grupo de simetría para un prisma n -gonal "regular" y también para una bipirámide n -gonal "regular" . D n d es el grupo de simetría para un antiprisma n -gonal "regular" , y también para un trapezoedro n -gonal "regular" . D n es el grupo de simetría de un prisma parcialmente rotado ("torcido").
Los grupos D 2 y D 2h son notables porque no tienen un eje de rotación especial, sino tres ejes perpendiculares de doble filo. D 2 es un subgrupo de todas las simetrías poliédricas (ver más abajo) y D 2h es un subgrupo de los grupos poliédricos T h y O h . D 2 se encuentra en moléculas como el twistano y en homotetrámeros como la concanavalina A . Los elementos de D 2 están en correspondencia 1 a 2 con las rotaciones dadas por los cuaterniones de Lipschitz unitarios .
El grupo S n se genera por la combinación de una reflexión en el plano horizontal y una rotación en un ángulo de 360°/n. Para n impar es igual al grupo generado por los dos por separado, C n h de orden 2 n , y por lo tanto no se necesita la notación S n ; sin embargo, para n par es distinto, y de orden n . Al igual que D n d contiene un número de rotaciones impropias sin contener las rotaciones correspondientes.
Todos los grupos de simetría en las 7 series infinitas son diferentes, excepto los siguientes cuatro pares de grupos mutuamente iguales:
- C 1h y C 1v : grupo de orden 2 con una única reflexión ( C s )
- D 1 y C 2 : grupo de orden 2 con una única rotación de 180°
- D 1h y C 2v : grupo de orden 4 con una reflexión en un plano y una rotación de 180° a través de una línea en ese plano
- D 1d y C 2h : grupo de orden 4 con una reflexión en un plano y una rotación de 180° a través de una línea perpendicular a ese plano.
S 2 es el grupo de orden 2 con una sola inversión ( C i ).
"Igual" se entiende aquí como lo mismo hasta la conjugación en el espacio. Esto es más fuerte que "hasta el isomorfismo algebraico". Por ejemplo, hay tres grupos diferentes de orden dos en el primer sentido, pero sólo hay uno en el segundo sentido. De manera similar, p. ej. S 2 n es algebraicamente isomorfo con Z 2 n .
Los grupos pueden construirse de la siguiente manera:
- C n . Generada por un elemento también llamado C n , que corresponde a una rotación de un ángulo 2π/ n alrededor del eje. Sus elementos son E (la identidad), C n , C n 2 , ..., C n n −1 , correspondientes a los ángulos de rotación 0, 2π/ n , 4π/ n , ..., 2( n − 1)π/ n .
- S 2 n . Generado por el elemento C 2 n σ h , donde σ h es una reflexión en la dirección del eje. Sus elementos son los elementos de C n con C 2 n σ h , C 2 n 3 σ h , ..., C 2 n 2 n −1 σ h añadido.
- C n h . Generado por el elemento C n y la reflexión σ h . Sus elementos son los elementos del grupo C n , con los elementos σ h , C n σ h , C n 2 σ h , ..., C n n −1 σ h añadidos.
- C n v . Generada por el elemento C n y la reflexión σ v en una dirección en el plano perpendicular al eje. Sus elementos son los elementos del grupo C n , con los elementos σ v , C n σ v , C n 2 σ v , ..., C n n −1 σ v añadidos.
- D n . Generado por el elemento C n y rotación de 180° U = σ h σ v alrededor de una dirección en el plano perpendicular al eje. Sus elementos son los elementos del grupo C n , con elementos U, C n U, C n 2 U, ..., C n n − 1 U añadidos.
- D n d . Generado por los elementos C 2 n σ h y σ v . Sus elementos son los elementos del grupo C n y los elementos adicionales de S 2 n y C n v , con los elementos C 2 n σ h σ v , C 2 n 3 σ h σ v , ..., C 2 n 2 n − 1 σ h σ v añadidos.
- D n h . Generado por los elementos C n , σ h y σ v . Sus elementos son los elementos del grupo C n y los elementos adicionales de C n h , C n v y D n .
Los grupos con rotaciones axiales continuas se designan poniendo ∞ en lugar de n . Sin embargo, tenga en cuenta que C ∞ aquí no es lo mismo que el grupo cíclico infinito (también designado a veces C ∞ ), que es isomorfo a los números enteros. La siguiente tabla muestra los cinco grupos de rotación axial continua. Son límites de los grupos finitos solo en el sentido de que surgen cuando la rotación principal se reemplaza por una rotación de un ángulo arbitrario, por lo que no necesariamente un número racional de grados como con los grupos finitos. Los objetos físicos solo pueden tener simetría C ∞v o D ∞h , pero los campos vectoriales pueden tener las otras.
| H-M | Moscas de Schön | Plegado orbi | Coxeter | Límite de | Grupo abstracto | |
|---|---|---|---|---|---|---|
| ∞ | C ∞ | ∞∞ | [∞] + |    | C n | SO(2) |
| ∞ , ∞/m | C∞h | ∞* | [2,∞ + ] |      | C n h , S 2 n | SO(2)× Z2 |
| ∞m | C∞v | *∞∞ | [∞] |    | Cnv | O(2) |
| ∞2 | D∞ | 22∞ | [2,∞] + |      | Dn | O(2) |
| ∞ metros, ∞/mm | D ∞h | *22∞ | [2,∞] |      | D n h , D n d | O(2)×Z 2 |
Los siete grupos de puntos restantes
Se dice que los grupos de puntos restantes son de simetría muy alta o poliédrica porque tienen más de un eje de rotación de orden mayor que 2. Aquí, C n denota un eje de rotación a través de 360°/n y S n denota un eje de rotación impropia a través del mismo. En líneas sucesivas están la notación orbifold , la notación de Coxeter y el diagrama de Coxeter , y la notación de Hermann-Mauguin (completa y abreviada si es diferente) y el orden (número de elementos) del grupo de simetría. Los grupos son:
| T , (332) [3,3] + (      ) ) 23 orden 12 | simetría tetraédrica quiral | Hay cuatro ejes C 3 , cada uno a través de dos vértices de un cubo circunscrito (cubo rojo en imágenes), o a través de un vértice de un tetraedro regular , y tres ejes C 2 , a través de los centros de las caras del cubo, o los puntos medios de las aristas del tetraedro. Este grupo es isomorfo a A 4 , el grupo alternante en 4 elementos, y es el grupo de rotación para un tetraedro regular. Es un subgrupo normal de T d , T h y las simetrías octaédricas. Los elementos del grupo corresponden 1 a 2 a las rotaciones dadas por los cuaterniones de Hurwitz de 24 unidades (el " grupo tetraédrico binario "). |
| T d , (*332) [3,3] (      ) ) 4 3m orden 24 | simetría tetraédrica completa | Este grupo es el grupo de simetría de un tetraedro regular . Este grupo tiene los mismos ejes de rotación que T , y los ejes C 2 son ahora ejes D 2d , mientras que los cuatro ejes triples dan lugar ahora a cuatro subgrupos C 3v . Este grupo tiene seis planos especulares, cada uno de los cuales contiene dos aristas del cubo o una arista del tetraedro, un solo eje S 4 y dos ejes C 3. T d es isomorfo a S 4 , el grupo simétrico de 4 letras, porque hay una correspondencia biunívoca entre los elementos de T d y las 24 permutaciones de los cuatro ejes triples. Un objeto de simetría C 3v bajo uno de los ejes triples da lugar, bajo la acción de T d, a una órbita que consta de cuatro de estos objetos, y T d corresponde al conjunto de permutaciones de estos cuatro objetos. T d es un subgrupo normal de O h . Véase también las isometrías del tetraedro regular . |
| T h , (3*2) [3 + ,4] (      ) ) 2/m 3 , m 3 orden 24 | simetría piritoédrica |  |
| O , (432) [4,3] + (      ) ) 432 orden 24 | simetría octaédrica quiral | Este grupo es como T , pero los ejes C 2 son ahora ejes C 4 , y además hay ejes de rotación dobles a través de los puntos medios de las aristas del cubo, dando lugar a tres subgrupos D 2 . Los ejes triples dan lugar ahora a cuatro subgrupos D 3 . Este grupo también es isomorfo a S 4 porque sus elementos están en correspondencia 1 a 1 con las 24 permutaciones de los ejes triples, como con T . Un objeto de simetría D 3 bajo uno de los ejes triples da lugar bajo la acción de O a una órbita que consta de cuatro de estos objetos, y O corresponde al conjunto de permutaciones de estos cuatro objetos. Es el grupo de rotación del cubo y el octaedro . Representando rotaciones con cuaterniones , O está formado por los 24 cuaterniones de Hurwitz unitarios y los 24 cuaterniones de Lipschitz de norma al cuadrado 2 normalizados al dividir por . Como antes, se trata de una correspondencia de 1 a 2. |
| Oh , ( * 432) [4,3] (      ) ) 4/m 3 2/m, m 3 m orden 48 | simetría octaédrica completa | Este grupo tiene los mismos ejes de rotación que O , pero con planos de simetría, que comprenden tanto los planos de simetría de T d como de T h . Los ejes triples dan lugar a cuatro subgrupos D 3d . Los tres ejes cuádruples perpendiculares de O dan ahora subgrupos D 4h , mientras que los seis ejes dobles dan seis subgrupos D 2h . Este grupo es isomorfo a S 4 × Z 2 (porque tanto O como C i son subgrupos normales), y es el grupo de simetría del cubo y del octaedro . Véase también las isometrías del cubo . |
| Yo , (532) [5,3] + (      ) ) 532 orden 60 | simetría icosaédrica quiral | Este es el grupo de rotación del icosaedro y el dodecaedro . Es un subgrupo normal de índice 2 en el grupo completo de simetrías I h . El grupo contiene 10 versiones de D 3 y 6 versiones de D 5 (simetrías rotacionales como prismas y antiprismas). También contiene cinco versiones de T (ver Compuesto de cinco tetraedros ). El grupo I es isomorfo a A 5 , el grupo alternado en 5 letras, ya que sus elementos se corresponden 1 a 1 con permutaciones pares de las cinco simetrías T (o los cinco tetraedros recién mencionados). Representando rotaciones con cuaterniones , I está formado por las 120 unidades icosianas . Como antes, esta es una correspondencia 1 a 2. |
| Yo soy , (*532) [5,3] (      ) ) 5 3 2/m, 5 3 m orden 120 | simetría icosaédrica completa | Este es el grupo de simetría del icosaedro y el dodecaedro. El grupo I h es isomorfo a A 5 × Z 2 porque I y C i son ambos subgrupos normales. El grupo contiene 10 versiones de D 3d , 6 versiones de D 5d (simetrías como antiprismas) y 5 versiones de T h . |
Los grupos continuos relacionados con estos grupos son:
- ∞∞, K o SO(3) , todas las rotaciones posibles.
- ∞∞m, K h , o O(3) , todas las rotaciones y reflexiones posibles.
Como se señaló anteriormente para los grupos de isometría infinitos, cualquier objeto físico que tenga simetría K también tendrá simetría K h .
Grupos reflexivos de Coxeter
Los grupos puntuales reflectantes en tres dimensiones también se denominan grupos de Coxeter y pueden representarse mediante un diagrama de Coxeter-Dynkin y representan un conjunto de espejos que se intersecan en un punto central. La notación de Coxeter ofrece una notación entre corchetes equivalente al diagrama de Coxeter, con símbolos de marcado para grupos puntuales de subsimetría rotacional y de otro tipo. En la notación de Schoenflies, los grupos puntuales reflectantes en 3D son C n v , D n h y los grupos poliédricos completos T , O e I .
Los planos especulares delimitan un conjunto de dominios de triángulos esféricos en la superficie de una esfera. Un grupo de Coxeter de rango n tiene n planos especulares. Los grupos de Coxeter que tienen menos de 3 generadores tienen dominios de triángulos esféricos degenerados, como un lunes o un hemisferio . En la notación de Coxeter, estos grupos son simetría tetraédrica [3,3], simetría octaédrica [4,3], simetría icosaédrica [5,3] y simetría diedra [p,2]. El número de espejos para un grupo irreducible es nh/2 , donde h es el número de Coxeter del grupo de Coxeter , n es la dimensión (3). [5]
Grupo Weyl | Notación de Coxeter | Orden | Número de Coxeter (h) | Espejos (m) | |
|---|---|---|---|---|---|
| Grupos poliédricos | |||||
| Un 3 |      | [3,3] | 24 | 4 | 6 |
| B3 |      | [4,3] | 48 | 6 | 3+6 |
| H3 |      | [5,3] | 120 | 10 | 15 |
| Grupos diedros | |||||
| 2 un 1 |    | [1,2] | 4 | 1+1 | |
| 3 un 1 |      | [2,2] | 8 | 2+1 | |
| Yo 2 (pág. 1) A 1 |      | [pág. 2] | 4p | pág. +1 | |
| Grupos cíclicos | |||||
| 2 un 1 |    | [2] | 4 | 2 | |
| Yo 2 (pág.) |    | [pag] | 2p | pag | |
| Espejo simple | |||||
| Un 1 |  | [ ] | 2 | 1 | |
Grupos de rotación
Los grupos de rotación, es decir, los subgrupos finitos de SO(3), son: los grupos cíclicos C n (el grupo de rotación de una pirámide canónica ), los grupos diedros D n (el grupo de rotación de un prisma uniforme, o bipirámide canónica ), y los grupos de rotación T , O e I de un tetraedro regular , octaedro / cubo e icosaedro / dodecaedro .
En particular, los grupos diedros D 3 , D 4 , etc. son los grupos de rotación de polígonos regulares planos insertos en el espacio tridimensional, y una figura de este tipo puede considerarse como un prisma regular degenerado. Por lo tanto, también se le llama diedro (del griego: sólido con dos caras), lo que explica el nombre de grupo diedro .
- Un objeto que tiene grupo de simetría C n , C n h , C n v o S 2 n tiene grupo de rotación C n .
- Un objeto que tiene un grupo de simetría D n , D n h o D n d tiene un grupo de rotación D n .
- Un objeto que tiene simetría poliédrica ( T , T d , T h , O , Oh h , I o I h ) tiene como grupo de rotación el correspondiente sin subíndice: T , O o I.
El grupo de rotación de un objeto es igual a su grupo de simetría completo si y solo si el objeto es quiral . En otras palabras, los objetos quirales son aquellos cuyo grupo de simetría se encuentra en la lista de grupos de rotación.
Dados en notación de Schönflies , notación de Coxeter ( notación orbifold ), los subgrupos de rotación son:
| Reflexión | Reflexión/rotación | Rotación incorrecta | Rotación |
|---|---|---|---|
| C n v , [n], (*nn) | C n h , [n + ,2], (n*) | S 2 n , [2n + ,2 + ], (n×) | C n , [n] + , (nn) |
| D n h , [2,n], (*n22) | D n d , [2 + ,2n], (2*n) | D n , [2,n] + , (n22) | |
| T d , [3,3], (*332) | T , [3,3] + , (332) | ||
| Oh , [4,3], (*432 ) | T h , [3 + ,4], (3*2) | O , [4,3] + , (432) | |
| Yo soy , [5,3], (*532) | Yo , [5,3] + , (532) |
Correspondencia entre grupos de rotación y otros grupos
Grupos que contienen inversión
El grupo de rotación SO(3) es un subgrupo de O(3), el grupo de rotación de puntos completo del espacio euclidiano 3D. En consecuencia, O(3) es el producto directo de SO(3) y el grupo de inversión C i (donde la inversión se denota por su matriz − I ):
- O(3) = SO(3) × { yo , − yo }
Por lo tanto, existe una correspondencia biunívoca entre todas las isometrías directas y todas las isometrías indirectas, mediante inversión. También existe una correspondencia biunívoca entre todos los grupos H de isometrías directas en SO(3) y todos los grupos K de isometrías en O(3) que contienen inversión:
- K = H × { yo , − yo }
- H = K ∩ SO(3)
donde la isometría ( A , I ) se identifica con A .
Para grupos finitos, la correspondencia es:
| Grupo de rotación H | Paridad de n | Grupo que contiene la inversión K |
|---|---|---|
| C n | incluso | Cnh |
| extraño | S 2 n | |
| Dn | incluso | D y H |
| extraño | D y d | |
| yo | El | |
| Oh | Oh | |
| I | Yo soy |
Grupos que contienen isometrías indirectas pero sin inversión
Si un grupo de isometrías directas H tiene un subgrupo L de índice 2, entonces hay un grupo correspondiente que contiene isometrías indirectas pero ninguna inversión:
Por ejemplo, H = C 4 corresponde a M = S 4 .
Por lo tanto, M se obtiene a partir de H invirtiendo las isometrías en . Este grupo M es, cuando se considera como un grupo abstracto , isomorfo a H . Por el contrario, para todos los grupos puntuales M que contienen isometrías indirectas pero ninguna inversión, podemos obtener un grupo de rotación H invirtiendo las isometrías indirectas.
Para grupos finitos, la correspondencia es:
| Grupo de rotación H | Índice-2 subgrupo L | Paridad de n | Grupo que contiene isometrías indirectas M |
|---|---|---|---|
| C2n | C n | incluso | S 2 n |
| extraño | Cnh | ||
| D 2 n | Dn | incluso | D y H |
| extraño | D y d | ||
| Dn | C n | cualquier | Cnv |
| Oh | yo | T.D. |
Subgrupos normales
En 2D, el grupo cíclico de rotaciones k -fold C k es para cada entero positivo k un subgrupo normal de O(2) y SO(2). En consecuencia, en 3D, para cada eje el grupo cíclico de rotaciones k -fold alrededor de ese eje es un subgrupo normal del grupo de todas las rotaciones alrededor de ese eje. Como cualquier subgrupo de índice dos es normal, el grupo de rotaciones ( C n ) es normal tanto en el grupo ( C n v ) obtenido sumando a ( C n ) planos de reflexión a través de su eje como en el grupo ( C n h ) obtenido sumando a ( C n ) un plano de reflexión perpendicular a su eje.
Simetrías máximas
Existen dos grupos puntuales discretos con la propiedad de que ningún grupo puntual discreto los tiene como subgrupo propio: O h e I h . Su mayor subgrupo común es T h . Los dos grupos se obtienen a partir de él cambiando la simetría rotacional de 2 veces a 4 veces y agregando simetría de 5 veces, respectivamente.
Existen dos grupos puntuales cristalográficos con la propiedad de que ningún grupo puntual cristalográfico los tiene como subgrupo propio: O h y D 6h . Sus subgrupos comunes máximos, dependiendo de la orientación, son D 3d y D 2h .
Los grupos ordenados por tipo de grupo abstracto
A continuación se organizan los grupos explicados anteriormente por tipo de grupo abstracto.
Los grupos abstractos más pequeños que no son ningún grupo de simetría en 3D, son el grupo de cuaterniones (de orden 8), Z 3 × Z 3 (de orden 9), el grupo dicíclico Dic 3 (de orden 12), y 10 de los 14 grupos de orden 16.
La columna "# de elementos de orden 2" en las siguientes tablas muestra el número total de subgrupos de isometría de los tipos C 2 , C i , C s . Este número total es una de las características que ayudan a distinguir los diversos tipos de grupos abstractos, mientras que su tipo de isometría ayuda a distinguir los diversos grupos de isometría de un mismo grupo abstracto.
Dentro de las posibilidades de los grupos de isometría en 3D, existen infinitos tipos de grupos abstractos con 0, 1 y 3 elementos de orden 2, hay dos con 4 n + 1 elementos de orden 2, y hay tres con 4 n + 3 elementos de orden 2 (para cada n ≥ 8). Nunca existe un número par positivo de elementos de orden 2.
Grupos de simetría en 3D que son cíclicos como grupo abstracto
El grupo de simetría para la simetría rotacional de n pliegues es C n ; su tipo de grupo abstracto es el grupo cíclico Z n , que también se denota por C n . Sin embargo, existen dos series infinitas más de grupos de simetría con este tipo de grupo abstracto:
- Para el orden par 2 n existe el grupo S 2 n (notación de Schoenflies) generado por una rotación de un ángulo de 180°/n alrededor de un eje, combinada con una reflexión en el plano perpendicular al eje. Para S 2 se utiliza la notación C i ; se genera por inversión.
- Para cualquier orden 2 n donde n es impar, tenemos C n h ; tiene un eje de rotación de n pliegues y un plano de reflexión perpendicular. Se genera por una rotación de un ángulo de 360°/ n alrededor del eje, combinada con la reflexión. Para C 1h se utiliza la notación C s ; se genera por reflexión en un plano.
Así tenemos, con negrita de los 10 grupos puntuales cristalográficos cíclicos, para los cuales se aplica la restricción cristalográfica :
| Orden | Grupos de isometría | Grupo abstracto | # de elementos de orden 2 | Diagrama de ciclo |
|---|---|---|---|---|
| 1 | C 1 | El 1 | 0 |  |
| 2 | C2 , C1 , Cs | El 2 | 1 |  |
| 3 | C 3 | Z3 | 0 | 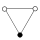 |
| 4 | C 4 , S 4 | Z4 | 1 |  |
| 5 | C 5 | Z5 | 0 |  |
| 6 | C6 , S6 , C3h | Z6 = Z3 × Z2 | 1 |  |
| 7 | C 7 | Z7 | 0 | 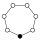 |
| 8 | C 8 , S 8 | Z8 | 1 | 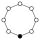 |
| 9 | C 9 | Z9 | 0 |  |
| 10 | C10 , S10 , C5h | Z10 = Z5 × Z2 | 1 |  |
etc.
Grupos de simetría en 3D que son diedros como grupo abstracto
En el grupo diedro 2D D n incluye reflexiones, que también pueden verse como giros de objetos planos sin distinción entre el lado frontal y el posterior.
Sin embargo, en 3D se distinguen las dos operaciones: el grupo de simetría denotado por D n contiene n ejes de 2 pliegues perpendiculares al eje de n pliegues, no reflexiones. D n es el grupo de rotación del prisma de n lados con base regular, y de la bipirámide de n lados con base regular, y también de un antiprisma regular de n lados y de un trapezoedro regular de n lados . El grupo es también el grupo de simetría completo de tales objetos después de hacerlos quirales mediante, por ejemplo, una marca quiral idéntica en cada cara, o alguna modificación en la forma.
El tipo de grupo abstracto es el grupo diedro Dih n , que también se denota por D n . Sin embargo, existen tres series infinitas más de grupos de simetría con este tipo de grupo abstracto:
- C n v de orden 2 n , el grupo de simetría de una pirámide regular de n lados
- D n d de orden 4 n , el grupo de simetría de un antiprisma regular de n lados
- D n h de orden 4 n para n impar . Para n = 1 obtenemos D 2 , ya tratado anteriormente, por lo que n ≥ 3.
Tenga en cuenta la siguiente propiedad:
- Dih 4 n + 2 Dih 2 n + 1 × Z 2
Así tenemos, con los 12 grupos puntuales cristalográficos en negrita y escribiendo D 1d como el C 2h equivalente :
| Orden | Grupos de isometría | Grupo abstracto | # de elementos de orden 2 | Diagrama de ciclo |
|---|---|---|---|---|
| 4 | re 2 , C 2v , C 2h | Dih2 = Z2 × Z2 | 3 |  |
| 6 | re 3 , do 3v | Di 3 | 3 |  |
| 8 | Re 4 , C 4v , Re 2d | Di 4 | 5 |  |
| 10 | re 5 , do 5v | Día 5 | 5 |  |
| 12 | D6 , C6v , D3d , D3h | Dih6 = Dih3 × Z2 | 7 | 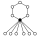 |
| 14 | Re 7 , Do 7v | Día 7 | 7 |  |
| 16 | Re 8 , C 8v , Re 4d | Día 8 | 9 |  |
| 18 | D 9 , C 9v | Día 9 | 9 | |
| 20 | D 10 , C 10 v , D 5 h , D 5 d | Dih 10 = D 5 × Z 2 | 11 |  |
etc.
Otro
C 2 n ,h de orden 4 n es del tipo de grupo abstracto Z 2 n × Z 2 . Para n = 1 obtenemos Dih 2 , ya tratado anteriormente, por lo que n ≥ 2.
Así tenemos, con negrita de los 2 grupos puntuales cristalográficos cíclicos:
| Orden | Grupo de isometría | Grupo abstracto | # de elementos de orden 2 | Diagrama de ciclo |
|---|---|---|---|---|
| 8 | C 4 horas | Z4 × Z2 | 3 |  |
| 12 | C 6 horas | Z 6 × Z 2 = Z 3 × Z 2 2 = Z 3 × Dih 2 | 3 |  |
| 16 | C 8 horas | Z8 × Z2 | 3 |  |
| 20 | C 10 horas | Z 10 × Z 2 = Z 5 × Z 2 2 = Z 5 × Dih 2 | 3 |  |
etc.
D n h de orden 4 n es de tipo de grupo abstracto Dih n × Z 2 . Para n impar esto ya se trató anteriormente, por lo que tenemos aquí D 2 n h de orden 8 n , que es de tipo de grupo abstracto Dih 2 n × Z 2 ( n ≥1).
Así tenemos, con negrita de los 3 grupos puntuales cristalográficos diedros:
| Orden | Grupo de isometría | Grupo abstracto | # de elementos de orden 2 | Diagrama de ciclo |
|---|---|---|---|---|
| 8 | D 2 horas | El 2 3 | 7 | 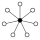 |
| 16 | D 4 horas | Di 4 × Z 2 | 11 | 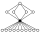 |
| 24 | D 6 horas | Dih 6 × Z 2 = Dih 3 × Z 2 2 | 15 | |
| 32 | D 8 horas | Dih 8 × Z 2 | 19 |
etc.
Los siete restantes son, con los 5 grupos puntuales cristalográficos resaltados en negrita (ver también arriba):
| Orden | Grupo de isometría | Grupo abstracto | # de elementos de orden 2 | Diagrama de ciclo |
|---|---|---|---|---|
| 12 | yo | Un 4 | 3 |  |
| 24 | T d , O | S 4 | 9 |  |
| 24 | El | Un 4 × Z 2 | 7 |  |
| 48 | Oh | S4 × Z2 | 19 | |
| 60 | I | Un 5 | 15 | |
| 120 | Yo soy | A 5 × Z 2 | 31 |
Dominio fundamental
 |  |
| Los planos de reflexión para la simetría icosaédrica intersecan la esfera en círculos máximos , con dominios fundamentales de triángulos esféricos rectángulos. | |
El dominio fundamental de un grupo de puntos es un sólido cónico . Un objeto con una simetría dada en una orientación dada se caracteriza por el dominio fundamental. Si el objeto es una superficie, se caracteriza por una superficie en el dominio fundamental que continúa hasta sus caras o superficies radiales bordales. Si las copias de la superficie no encajan, se pueden agregar caras o superficies radiales. De todos modos, encajan si el dominio fundamental está limitado por planos de reflexión.
Para un poliedro, esta superficie en el dominio fundamental puede ser parte de un plano arbitrario. Por ejemplo, en el triacontaedro de Disdyakis, una cara completa es un dominio fundamental de simetría icosaédrica . Ajustar la orientación del plano da varias posibilidades de combinar dos o más caras adyacentes en una, dando lugar a varios otros poliedros con la misma simetría. El poliedro es convexo si la superficie se ajusta a sus copias y la línea radial perpendicular al plano está en el dominio fundamental.
También la superficie en el dominio fundamental puede estar compuesta de múltiples caras.
Grupos poliédricos binarios
La función Spin(3) → SO(3) es la doble cobertura del grupo de rotación por el grupo de espín en 3 dimensiones. (Esta es la única cobertura conexa de SO(3), ya que Spin(3) es simplemente conexo.) Por el teorema de red , existe una conexión de Galois entre subgrupos de Spin(3) y subgrupos de SO(3) (grupos puntuales rotacionales): la imagen de un subgrupo de Spin(3) es un grupo puntual rotacional, y la preimagen de un grupo puntual es un subgrupo de Spin(3). (Obsérvese que Spin(3) tiene descripciones alternativas como el grupo unitario especial SU(2) y como el grupo de cuaterniones unitarios . Topológicamente, este grupo de Lie es la esfera tridimensional S 3 .)
La preimagen de un grupo puntual finito se denomina grupo poliédrico binario , representado como ⟨l,n,m⟩, y recibe el mismo nombre que su grupo puntual, con el prefijo binario , con el doble del orden del grupo poliédrico relacionado (l,m,n). Por ejemplo, la preimagen del grupo icosaédrico (2,3,5) es el grupo icosaédrico binario , ⟨2,3,5⟩.
Los grupos poliédricos binarios son:
- : grupo cíclico binario de un ( n + 1)-gono, orden 2 n
- : grupo diedro binario de un n -gono, ⟨2,2, n ⟩, orden 4 n
- : grupo tetraédrico binario , ⟨2,3,3⟩, orden 24
- : grupo octaédrico binario , ⟨2,3,4⟩, orden 48
- : grupo icosaédrico binario , ⟨2,3,5⟩, orden 120
Estos se clasifican mediante la clasificación ADE , y el cociente de C 2 por la acción de un grupo poliédrico binario es una singularidad de Du Val . [6]
Para los grupos de puntos que invierten la orientación, la situación es más complicada, ya que hay dos grupos de pines , por lo que hay dos grupos binarios posibles correspondientes a un grupo de puntos dado.
Nótese que se trata de una cobertura de grupos, no de espacios : la esfera está simplemente conexa y, por lo tanto, no tiene espacios de cobertura . Por lo tanto, no existe la noción de un "poliedro binario" que cubra un poliedro tridimensional. Los grupos poliédricos binarios son subgrupos discretos de un grupo de espín y, bajo una representación del grupo de espín, actúan sobre un espacio vectorial y pueden estabilizar un poliedro en esta representación: bajo la función Spin(3) → SO(3), actúan sobre el mismo poliedro sobre el que actúa el grupo subyacente (no binario), mientras que, bajo representaciones de espín u otras representaciones, pueden estabilizar otros poliedros.
Esto contrasta con los poliedros proyectivos : la esfera cubre el espacio proyectivo (y también los espacios lenticulares ) y, por lo tanto, una teselación del espacio proyectivo o del espacio lenticular produce una noción distinta de poliedro.
Véase también
- Lista de grupos de simetría esférica
- Lista de tablas de caracteres para grupos de puntos 3D de importancia química
- Grupos de puntos en dos dimensiones
- Grupos de puntos en cuatro dimensiones
- Simetría
- Isometría del plano euclidiano
- Acción grupal
- Grupo de puntos
- Sistema de cristal
- Grupo espacial
- Lista de grupos pequeños
- Simetría molecular
Notas al pie
- ^ ab Curie, Pierre (1894). "Sur la symétrie dans les phénomènes physiques, symétrie d'un champ électrique et d'un champ magnétique" [Sobre la simetría en los fenómenos físicos, simetría de un campo eléctrico y de un campo magnético] (PDF) . Journal de Physique (en francés). 3 (1): 393–415. doi :10.1051/jphystap:018940030039300.
- ^ Shubnikov, AV (1988). "Sobre los trabajos de Pierre Curie sobre simetría". Simetrías de cristales: artículos del centenario de Shubnikov . Pergamon Press. págs. 357–364. doi :10.1016/B978-0-08-037014-9.50007-8. ISBN . 0-08-037014-4.
- ^ Vainshtein., BK (1994). Cristalografía moderna, vol. 1. Fundamentos de cristales. Simetría y métodos de cristalografía estructural (2.ª edición ampliada). Springer-Verlag Berlin. pág. 93. ISBN 978-3-642-08153-8.
- ^ Fisher, GL; Mellor, B. (2007), "Grupos puntuales finitos tridimensionales y simetría de cuentas" (PDF) , Journal of Mathematics and the Arts , 1 (2): 85–96, doi :10.1080/17513470701416264, S2CID 40755219
- ^ Coxeter , Politopos regulares , §12.6 El número de reflexiones, ecuación 12.61
- ^ Burban, Igor. "Singularidades de Du Val" (PDF) .
Referencias
Este artículo necesita citas adicionales para su verificación . ( mayo de 2010 ) |
- Coxeter, HSM (1974), "7 Los grupos poliédricos binarios", Regular Complex Polytopes , Cambridge University Press, págs. 73–82.
- Coxeter, HSM y Moser, WOJ (1980). Generadores y relaciones para grupos discretos, 4.ª edición . Nueva York: Springer-Verlag. ISBN 0-387-09212-9.6.5 Los grupos poliédricos binarios, pág. 68
- Conway, John Horton ; Huson, Daniel H. (2002), "La notación orbifold para grupos bidimensionales", Química estructural , 13 (3), Springer Netherlands: 247–257, doi :10.1023/A:1015851621002, S2CID 33947139
Enlaces externos
- Resumen gráfico de los 32 grupos puntuales cristalográficos: forman las primeras partes (aparte de omitir n = 5) de las 7 series infinitas y 5 de los 7 grupos puntuales 3D separados
- Descripción general de las propiedades de los grupos de puntos
- Poliedros canónicos más simples de cada tipo de simetría (usa Java)
- Grupos puntuales y sistemas cristalinos, por Yi-Shu Wei, págs. 4-6
- El Centro de Geometría: 10.1 Fórmulas para Simetrías en Coordenadas Cartesianas (tres dimensiones)