Balística externa
La balística externa o balística exterior es la parte de la balística que estudia el comportamiento de un proyectil en vuelo. El proyectil puede ser propulsado o no, guiado o no, estabilizado por giro o por aletas, volar a través de una atmósfera o en el vacío del espacio, pero con toda seguridad volar bajo la influencia de un campo gravitatorio. [1]
Los proyectiles lanzados con cañones pueden no tener motor, y derivar toda su velocidad de la ignición del propulsor hasta que el proyectil sale del cañón del cañón . [2] Sin embargo, el análisis balístico externo también se ocupa de las trayectorias de los proyectiles lanzados con cañones asistidos por cohetes y los cohetes lanzados con cañones; y de los cohetes que adquieren toda su velocidad de trayectoria de la balística interior de su sistema de propulsión de a bordo, ya sea un motor de cohete o un motor de aire, tanto durante su fase de impulso como después de que el motor se queme. La balística externa también se ocupa del vuelo libre de otros proyectiles, como bolas , flechas , etc.
Fuerzas que actúan sobre el proyectil
Durante el vuelo, las fuerzas principales que actúan sobre el proyectil son la gravedad , la resistencia y, si está presente, el viento ; si está en vuelo propulsado, el empuje; y si está guiado, las fuerzas impartidas por las superficies de control.
En las aplicaciones de balística externa de armas pequeñas, la gravedad imparte una aceleración hacia abajo sobre el proyectil, lo que hace que caiga de la línea de visión . La resistencia al avance , o la resistencia del aire, desacelera el proyectil con una fuerza proporcional al cuadrado de la velocidad. El viento hace que el proyectil se desvíe de su trayectoria. Durante el vuelo, la gravedad, la resistencia al avance y el viento tienen un gran impacto en la trayectoria del proyectil y deben tenerse en cuenta al predecir cómo viajará el proyectil.
Para distancias y tiempos de vuelo medianos y largos, además de la gravedad, la resistencia del aire y el viento, se deben tener en cuenta varias variables intermedias o meso descritas en el párrafo de factores externos para las armas pequeñas. Las variables meso pueden resultar significativas para los usuarios de armas de fuego que tienen que lidiar con escenarios de disparos en ángulo o distancias extendidas, pero rara vez son relevantes en las distancias comunes de caza y tiro al blanco.
En el caso de los blancos de armas pequeñas con alcances y tiempos de vuelo largos o muy largos, los efectos y fuerzas menores, como los descritos en el párrafo sobre los factores de largo alcance, se vuelven importantes y deben tenerse en cuenta. Los efectos prácticos de estas variables menores son generalmente irrelevantes para la mayoría de los usuarios de armas de fuego, ya que la dispersión normal del grupo a distancias cortas y medias prevalece sobre la influencia que estos efectos ejercen sobre las trayectorias de los proyectiles .
A distancias extremadamente largas, la artillería debe disparar proyectiles a lo largo de trayectorias que ni siquiera son aproximadamente rectas; son más cercanas a las parabólicas , aunque la resistencia del aire afecta esto. Los proyectiles de alcance extremadamente largo están sujetos a desviaciones significativas, según las circunstancias, de la línea hacia el objetivo; y todos los factores externos y de largo alcance deben tenerse en cuenta al apuntar. En casos de artillería de calibre muy grande , como el cañón de París , efectos muy sutiles que no se tratan en este artículo pueden refinar aún más las soluciones de puntería.
En el caso de los misiles balísticos , las altitudes involucradas también tienen un efecto significativo, ya que parte del vuelo se lleva a cabo en un pozo casi al vacío sobre una Tierra en rotación, moviendo constantemente el objetivo desde donde estaba en el momento del lanzamiento.
Estabilización de proyectiles no esféricos durante el vuelo
Se pueden emplear dos métodos para estabilizar proyectiles no esféricos durante el vuelo:
- Los proyectiles como flechas o sabots similares a flechas , como el M829 Armor-Piercing, Fin-Stabilized, Discarding Sabot (APFSDS) logran estabilidad al forzar su centro de presión (CP) detrás de su centro de masa (CM) con superficies de cola. La condición CP detrás del CM produce un vuelo estable del proyectil, lo que significa que el proyectil no se volcará durante el vuelo a través de la atmósfera debido a las fuerzas aerodinámicas.
- Los proyectiles, como las balas de armas pequeñas y los proyectiles de artillería, deben lidiar con el hecho de que su CP está delante de su CM, lo que desestabiliza estos proyectiles durante el vuelo. Para estabilizar estos proyectiles, el proyectil gira alrededor de su eje longitudinal (de entrada a salida). La masa giratoria crea fuerzas giroscópicas que mantienen el eje longitudinal de la bala resistente al par de vuelco desestabilizador del CP que está delante del CM.
Efectos principales en balística externa
Caída del proyectil/bala y trayectoria del proyectil

El efecto de la gravedad sobre un proyectil en vuelo se conoce a menudo como caída del proyectil o caída de la bala. Es importante comprender el efecto de la gravedad al poner a cero los componentes de puntería de un arma. Para planificar la caída del proyectil y compensarla adecuadamente, uno debe comprender las trayectorias con forma parabólica .
Caída de proyectil/bala
Para que un proyectil impacte en un objetivo distante, el cañón debe estar inclinado en un ángulo de elevación positivo con respecto al objetivo. Esto se debe al hecho de que el proyectil comenzará a responder a los efectos de la gravedad en el instante en que se libere de las restricciones mecánicas del ánima. La línea imaginaria que baja por el eje central del ánima y se extiende hasta el infinito se denomina línea de salida y es la línea por la que el proyectil sale del cañón. Debido a los efectos de la gravedad, un proyectil nunca puede impactar en un objetivo que se encuentre por encima de la línea de salida. Cuando un proyectil con inclinación positiva se desplaza hacia abajo, describe un arco por debajo de la línea de salida, ya que la gravedad lo desvía de su trayectoria inicial. La caída del proyectil/bala se define como la distancia vertical del proyectil por debajo de la línea de salida desde el ánima. Incluso cuando la línea de salida está inclinada hacia arriba o hacia abajo, la caída del proyectil se define como la distancia entre la bala y la línea de salida en cualquier punto a lo largo de la trayectoria. La caída del proyectil no describe la trayectoria real del proyectil. Sin embargo, el conocimiento de la caída de proyectiles es útil cuando se realiza una comparación directa de dos proyectiles diferentes con respecto a la forma de sus trayectorias, comparando los efectos de variables como la velocidad y el comportamiento de arrastre.
Trayectoria del proyectil/bala
Para alcanzar un objetivo distante se requiere un ángulo de elevación positivo apropiado que se logra inclinando la línea de visión desde el ojo del tirador a través de la línea central del sistema de mira hacia abajo en dirección a la línea de partida. Esto se puede lograr simplemente ajustando las miras hacia abajo mecánicamente, o asegurando todo el sistema de mira a un montaje inclinado que tenga una pendiente descendente conocida, o mediante una combinación de ambos. Este procedimiento tiene el efecto de elevar la boca del cañón cuando el cañón debe elevarse posteriormente para alinear las miras con el objetivo. Un proyectil que sale de la boca del cañón en un ángulo de elevación dado sigue una trayectoria balística cuyas características dependen de varios factores como la velocidad inicial, la gravedad y la resistencia aerodinámica. Esta trayectoria balística se conoce como la trayectoria de la bala. Si el proyectil está estabilizado por giro, las fuerzas aerodinámicas también arquearán previsiblemente la trayectoria ligeramente hacia la derecha, si el estriado emplea "torsión a la derecha". Algunos cañones están cortados con torsión a la izquierda y, como resultado, la bala se arqueará hacia la izquierda. Por lo tanto, para compensar esta desviación de la trayectoria, las miras también deben ajustarse a la izquierda o a la derecha, respectivamente. Un viento constante también afecta previsiblemente la trayectoria de la bala, empujándola ligeramente a la izquierda o a la derecha, y un poco más hacia arriba y hacia abajo, dependiendo de la dirección del viento. La magnitud de estas desviaciones también se ve afectada por si la bala está en la pendiente ascendente o descendente de la trayectoria, debido a un fenómeno llamado "guiñada de reposo", donde una bala giratoria tiende a alinearse de manera constante y previsible ligeramente fuera del centro de su trayectoria de masa puntual. Sin embargo, cada una de estas perturbaciones de la trayectoria son predecibles una vez que se establecen los coeficientes aerodinámicos del proyectil, a través de una combinación de modelado analítico detallado y mediciones de rango de prueba.
El análisis de la trayectoria de los proyectiles y las balas es de gran utilidad para los tiradores, ya que les permite establecer tablas balísticas que predecirán cuántas correcciones de elevación vertical y desviación horizontal se deben aplicar a la línea de visión para disparos a varias distancias conocidas. Las tablas balísticas más detalladas se desarrollan para la artillería de largo alcance y se basan en un análisis de trayectoria de seis grados de libertad, que tiene en cuenta el comportamiento aerodinámico a lo largo de las tres direcciones axiales (elevación, alcance y desviación) y las tres direcciones de rotación (cabeceo, guiñada y giro). Para aplicaciones de armas pequeñas, el modelado de la trayectoria a menudo se puede simplificar a cálculos que involucran solo cuatro de estos grados de libertad, agrupando los efectos de cabeceo, guiñada y giro en el efecto de una guiñada de reposo para tener en cuenta la desviación de la trayectoria. Una vez que se establecen tablas de alcance detalladas, los tiradores pueden ajustar con relativa rapidez las miras en función de la distancia al objetivo, el viento, la temperatura y la humedad del aire y otras consideraciones geométricas, como las diferencias de elevación del terreno.
Los valores de la trayectoria del proyectil se determinan tanto por la altura de la mira, o la distancia de la línea de mira por encima de la línea central del cañón, como por el rango en el que se ponen a cero las miras, lo que a su vez determina el ángulo de elevación. Un proyectil que sigue una trayectoria balística tiene un movimiento tanto hacia adelante como vertical. El movimiento hacia adelante se ralentiza debido a la resistencia del aire, y en el modelado de masas puntuales el movimiento vertical depende de una combinación del ángulo de elevación y la gravedad. Inicialmente, el proyectil se eleva con respecto a la línea de mira o al plano de mira horizontal. El proyectil finalmente alcanza su vértice (el punto más alto en la parábola de la trayectoria) donde el componente de velocidad vertical decae a cero bajo el efecto de la gravedad, y luego comienza a descender, impactando finalmente la tierra. Cuanto mayor sea la distancia al objetivo previsto, mayor será el ángulo de elevación y más alto el vértice.
La trayectoria del proyectil cruza el plano de puntería horizontal dos veces. El punto más cercano al arma se produce cuando la bala asciende por la línea de puntería y se denomina cero cercano. El segundo punto se produce cuando el proyectil desciende por la línea de puntería. Se denomina cero lejano y define la distancia de puntería actual del arma. La trayectoria del proyectil se describe numéricamente como distancias por encima o por debajo del plano de puntería horizontal en varios puntos a lo largo de la trayectoria. Esto contrasta con la caída del proyectil, que se refiere al plano que contiene la línea de partida independientemente del ángulo de elevación. Dado que cada uno de estos dos parámetros utiliza un dato de referencia diferente, puede producirse una confusión importante porque, aunque un proyectil se desplace muy por debajo de la línea de partida, puede seguir ganando altura real y significativa con respecto a la línea de puntería, así como a la superficie de la Tierra en el caso de un disparo horizontal o casi horizontal realizado sobre terreno llano.
Alcance máximo a quemarropa y batalla cero
El conocimiento de la caída y la trayectoria del proyectil tiene algunas utilidades prácticas para los tiradores, incluso si no describe la trayectoria real del proyectil. Por ejemplo, si la posición vertical del proyectil en un cierto rango de alcance está dentro de la altura vertical del área del objetivo que el tirador quiere alcanzar, el punto de mira no necesariamente necesita ajustarse en ese rango; se considera que el proyectil tiene una trayectoria a quemarropa suficientemente plana para ese objetivo en particular. [3] También conocido como "cero de batalla", el alcance máximo a quemarropa también es importante para el ejército. A los soldados se les instruye que disparen a cualquier objetivo dentro de este rango simplemente colocando la mira de su arma en el centro de masa del objetivo enemigo. Cualquier error en la estimación del alcance es tácticamente irrelevante, ya que un disparo bien apuntado impactará en el torso del soldado enemigo. La tendencia actual a usar miras elevadas y cartuchos de mayor velocidad en los rifles de asalto se debe en parte al deseo de extender el alcance máximo a quemarropa, lo que hace que el rifle sea más fácil de usar. [4] [5] [6]
Resistencia al arrastre

Los modelos matemáticos , como la dinámica de fluidos computacional, se utilizan para calcular los efectos de la resistencia aerodinámica o del aire; son bastante complejos y aún no completamente confiables, pero la investigación está en curso. [7] Por lo tanto, el método más confiable para establecer las propiedades aerodinámicas de los proyectiles necesarias para describir adecuadamente las trayectorias de vuelo es mediante la medición empírica.
Modelos de curva de arrastre fija generados para proyectiles de forma estándar

El uso de tablas balísticas o software balístico basado en el método Mayevski/Siacci y el modelo de arrastre G1 , introducido en 1881, es el método más común utilizado para trabajar con balística externa. Los proyectiles se describen mediante un coeficiente balístico , o BC, que combina la resistencia del aire de la forma de la bala (el coeficiente de arrastre ) y su densidad seccional (una función de la masa y el diámetro de la bala).
La desaceleración debida a la resistencia que experimentará un proyectil con masa m , velocidad v y diámetro d es proporcional a 1/BC, 1/ m , v² y d² . El BC da la relación de la eficiencia balística en comparación con el proyectil estándar G1, que es un proyectil ficticio con una base plana, una longitud de 3,28 calibres/diámetros y una curva tangencial de radio de 2 calibres/diámetros para la punta. El proyectil estándar G1 se origina a partir del proyectil de referencia estándar "C" definido por el fabricante alemán de acero, municiones y armamento Krupp en 1881. El proyectil estándar modelo G1 tiene un BC de 1. [8] La Comisión Gâvre francesa decidió utilizar este proyectil como su primer proyectil de referencia, dándole el nombre de G1. [9] [10]
Las balas deportivas, con un calibre d que va de 0,177 a 0,50 pulgadas (4,50 a 12,7 mm ), tienen un BC G1 en el rango de 0,12 a un poco más de 1,00, siendo 1,00 el más aerodinámico y 0,12 el menos. Las balas de muy baja resistencia con BC ≥ 1,10 se pueden diseñar y producir en tornos de precisión CNC a partir de varillas monometálicas, pero a menudo tienen que dispararse desde rifles de calibre completo hechos a medida con cañones especiales. [11]
La densidad seccional es un aspecto muy importante de un proyectil o bala, y para un proyectil redondo como una bala es la relación entre el área de la superficie frontal (la mitad del diámetro de la bala al cuadrado, multiplicado por pi ) y la masa de la bala. Dado que, para una forma de bala determinada, la superficie frontal aumenta con el cuadrado del calibre y la masa aumenta con el cubo del diámetro, la densidad seccional crece linealmente con el diámetro del ánima. Dado que la densidad seccional combina la forma y la densidad seccional, un modelo a media escala del proyectil G1 tendrá una densidad seccional de 0,5 y un modelo a un cuarto de escala tendrá una densidad seccional de 0,25.
Dado que las diferentes formas de proyectiles responderán de manera diferente a los cambios de velocidad (en particular entre velocidades supersónicas y subsónicas ), un BC proporcionado por un fabricante de balas será un BC promedio que representa el rango común de velocidades para esa bala. Para balas de rifle , esta será probablemente una velocidad supersónica , para balas de pistola probablemente será subsónica. Para proyectiles que viajan a través de los regímenes de vuelo supersónico , transónico y subsónico, BC no se aproxima bien por una sola constante, sino que se considera una función BC(M) del número de Mach M; aquí M es igual a la velocidad del proyectil dividida por la velocidad del sonido . Durante el vuelo del proyectil, M disminuirá y, por lo tanto (en la mayoría de los casos) el BC también disminuirá.
La mayoría de las tablas balísticas o el software dan por sentado que una función de arrastre específica describe correctamente la resistencia y, por lo tanto, las características de vuelo de una bala en relación con su coeficiente balístico. Esos modelos no diferencian entre tipos o formas de balas wadcutter , flat-based, spitzer, boat-tail, very-low-drag , etc. Suponen una función de arrastre invariable, como lo indica el BC publicado.
Sin embargo, existen varios modelos de curva de arrastre optimizados para varias formas estándar de proyectiles. Los modelos de curva de arrastre fijos resultantes para varias formas o tipos estándar de proyectiles se denominan:

- G1 o Ingalls (base plana con ojiva de calibre 2 (roma), por lejos la más popular)
- G2 (proyectil Aberdeen J)
- G5 (cola de barco corta de 7,5°, ojiva tangente larga de calibre 6,19 )
- G6 (base plana, ojiva secante larga de 6 calibres )
- G7 (cola de barco larga de 7,5°, ojiva tangente de calibre 10, preferida por algunos fabricantes para balas de muy baja resistencia [12] )
- G8 (base plana, ojiva secante larga de 10 calibres)
- GL (punta de plomo roma)
En el folleto del producto Lapua Magnum .338 se puede ver cómo los diferentes regímenes de velocidad afectan a las balas de rifle de calibre .338, que indica que los datos de BC G1 establecidos por radar Doppler. [13] [14] La razón para publicar datos como los de este folleto es que el modelo G1 de Siacci/Mayevski no se puede ajustar para el comportamiento de arrastre de un proyectil específico cuya forma se desvía significativamente de la forma de proyectil de referencia utilizada. Algunos diseñadores de software balístico, que basaron sus programas en el modelo G1 de Siacci/Mayevski, le dan al usuario la posibilidad de ingresar varias constantes BC G1 diferentes para diferentes regímenes de velocidad para calcular predicciones balísticas que se acerquen más al comportamiento de vuelo de las balas a distancias más largas en comparación con los cálculos que usan solo una constante BC.
El ejemplo anterior ilustra el problema central que tienen los modelos de curva de arrastre fija. Estos modelos solo producirán predicciones precisas satisfactorias siempre que el proyectil de interés tenga la misma forma que el proyectil de referencia o una forma que se parezca mucho al proyectil de referencia. Cualquier desviación de la forma del proyectil de referencia dará como resultado predicciones menos precisas. [15] [16] La desviación de un proyectil con respecto al proyectil de referencia aplicado se expresa matemáticamente mediante el factor de forma ( i ). [17] El factor de forma se puede utilizar para comparar la desviación experimentada por un proyectil de interés con la desviación experimentada por el proyectil de referencia empleado a una velocidad (rango) dada. El problema de que la curva de arrastre real de un proyectil puede desviarse significativamente de la curva de arrastre fija de cualquier proyectil de referencia empleado limita sistemáticamente el enfoque tradicional de modelado de resistencia al arrastre. Sin embargo, la relativa simplicidad hace que pueda ser explicada y entendida por el público general de tiro y, por lo tanto, también es popular entre los desarrolladores de predicción de software balístico y los fabricantes de balas que desean comercializar sus productos.
Modelos de arrastre más avanzados
Modelo Pejsa
Otro intento de construir una calculadora balística es el modelo presentado en 1980 por el Dr. Arthur J. Pejsa. [18] El Dr. Pejsa afirma en su sitio web que su método fue consistentemente capaz de predecir trayectorias de balas de rifle (supersónicas) dentro de 2,5 mm (0,1 pulgadas) y velocidades de bala dentro de 0,3 m/s (1 pie/s) hasta 914 m (1000 yardas) en teoría. [19] El modelo de Pejsa es una solución de forma cerrada .
El modelo Pejsa puede predecir un proyectil dentro de un régimen de vuelo dado (por ejemplo, el régimen de vuelo supersónico) con solo dos mediciones de velocidad, una distancia entre dichas mediciones de velocidad y un factor de pendiente o constante de desaceleración. [20] El modelo permite que la curva de arrastre cambie las pendientes (verdadera/calibrada) o la curvatura en tres puntos diferentes. [21] Los datos de medición de velocidad de rango descendente se pueden proporcionar alrededor de puntos de inflexión clave, lo que permite cálculos más precisos de la tasa de retardo del proyectil, muy similar a una tabla de Mach vs CD. El modelo Pejsa permite ajustar el factor de pendiente para tener en cuenta las diferencias sutiles en la tasa de retardo de diferentes formas y tamaños de bala. Varía de 0,1 (balas de punta plana) a 0,9 ( balas de muy baja resistencia ). Si se desconoce este factor de pendiente o constante de desaceleración, se utiliza un valor predeterminado de 0,5. Con la ayuda de mediciones de disparos de prueba, se puede determinar la constante de pendiente para una combinación particular de bala/sistema de rifle/tirador. Estos disparos de prueba se deben ejecutar preferiblemente al 60% y, para predicciones balísticas de alcance extremadamente largo, también al 80% o 90% del alcance supersónico de los proyectiles de interés, evitando los efectos transónicos erráticos. Con esto, el modelo Pejsa se puede ajustar fácilmente. Una desventaja práctica del modelo Pejsa es que la gran mayoría de los entusiastas del tiro no pueden realizar fácilmente mediciones precisas de la velocidad de alcance específico del proyectil para proporcionar estas mejores predicciones.
Se puede calcular un coeficiente de retardo promedio para cualquier factor constante de pendiente dado si se conocen los puntos de datos de velocidad y se conoce la distancia entre dichas mediciones de velocidad. Obviamente, esto es cierto solo dentro del mismo régimen de vuelo. Con velocidad se entiende la velocidad real , ya que la velocidad es una cantidad vectorial y la velocidad es la magnitud del vector de velocidad. Debido a que la función de potencia no tiene una curvatura constante, no se puede utilizar un promedio de cuerda simple . El modelo Pejsa utiliza un coeficiente de retardo promedio ponderado ponderado en un rango de 0,25. La velocidad más cercana tiene una ponderación mayor. El coeficiente de retardo se mide en pies, mientras que el rango se mide en yardas, por lo tanto, 0,25 × 3,0 = 0,75; en algunos lugares se utiliza 0,8 en lugar de 0,75. El 0,8 proviene del redondeo para permitir una entrada fácil en calculadoras manuales. Dado que el modelo Pejsa no utiliza un promedio ponderado de cuerda simple, se utilizan dos mediciones de velocidad para encontrar el coeficiente de retardo promedio de cuerda en el rango medio entre los dos puntos de medición de velocidad, lo que lo limita a una precisión de corto alcance. Para encontrar el coeficiente de retardo inicial, el Dr. Pejsa proporciona dos ecuaciones separadas en sus dos libros. La primera involucra la función de potencia. [22] La segunda ecuación es idéntica a la utilizada para encontrar el promedio ponderado en R / 4; agregue N × (R/2) donde R es el rango en pies al coeficiente de retardo promedio de la cuerda en el rango medio y donde N es el factor constante de pendiente. [23] Después de encontrar el coeficiente de retardo inicial, se utiliza el procedimiento opuesto para encontrar el promedio ponderado en R / 4; el coeficiente de retardo inicial menos N × (R/4). En otras palabras, N se utiliza como la pendiente de la línea de cuerda. El Dr. Pejsa afirma que expandió su fórmula de caída en una serie de potencias para demostrar que el coeficiente de retardo promedio ponderado en R / 4 era una buena aproximación. Para esto, el Dr. Pejsa comparó la expansión de la serie de potencias de su fórmula de caída con la expansión de potencia de alguna otra fórmula de caída sin nombre para llegar a sus conclusiones. El cuarto término en ambas series de potencias coincidió cuando se utilizó el coeficiente de retardo en el rango de 0,25 en la fórmula de caída de Pejsa. El cuarto término también fue el primer término en utilizar N. Los términos superiores que involucraban a N fueron insignificantes y desaparecieron en N = 0,36, lo que según el Dr. Pejsa fue una coincidencia afortunada que generó una aproximación lineal extremadamente precisa, especialmente para N en torno a 0,36. Si se utiliza una función de coeficiente de retardo, se pueden obtener valores promedio exactos para cualquier N porque a partir del cálculo es trivial encontrar el promedio de cualquier función integrable . [24] El Dr. Pejsa afirma que el coeficiente de retardo se puede modelar mediante C × V Ndonde C es un coeficiente de ajuste que desaparece durante la derivación de la fórmula de caída y N el factor constante de pendiente. [25]
El coeficiente de retardo es igual a la velocidad al cuadrado dividida por la tasa de retardo A. El uso de un coeficiente de retardo promedio permite que el modelo Pejsa sea una expresión de forma cerrada dentro de un régimen de vuelo determinado.

Para permitir el uso de un coeficiente balístico G1 en lugar de datos de velocidad, el Dr. Pejsa proporcionó dos curvas de resistencia de referencia. La primera curva de resistencia de referencia se basa puramente en la función de tasa de retardo de Siacci/Mayevski. La segunda curva de resistencia de referencia se ajusta para que sea igual a la función de tasa de retardo de Siacci/Mayevski a una velocidad de proyectil de 2600 fps (792,5 m/s) utilizando una bala Spitzer de rifle de 152 granos (9,8 g) con cartucho Springfield .30-06, bala, calibre .30 M2 con un factor de pendiente o constante de desaceleración de 0,5 en el régimen de vuelo supersónico. En otros regímenes de vuelo, el segundo modelo de curva de resistencia de referencia de Pejsa utiliza factores de pendiente constante de 0,0 o -4,0. Estos factores constantes de desaceleración se pueden verificar retrocediendo las fórmulas de Pejsa (los segmentos de la curva de arrastre se ajustan a la forma V (2 - N) / C y los segmentos de la curva del coeficiente de retardo se ajustan a la forma V 2 / (V (2 - N) / C) = C × V N donde C es un coeficiente de ajuste). Los datos de prueba empírica que Pejsa utilizó para determinar la forma exacta de su curva de arrastre de referencia elegida y la función matemática predefinida que devuelve el coeficiente de retardo en un número de Mach dado fueron proporcionados por el ejército de los EE. UU. para la bala de cartucho, bola, calibre .30 M2. El cálculo de la función del coeficiente de retardo también involucra la densidad del aire, que Pejsa no mencionó explícitamente. El modelo Siacci/Mayevski G1 utiliza la siguiente parametrización de desaceleración (60 °F, 30 inHg y 67% de humedad, densidad del aire ρ = 1,2209 kg/m 3 ). [26] El Dr. Pejsa sugiere utilizar la segunda curva de arrastre porque la curva de arrastre Siacci/Mayevski G1 no se ajusta bien a las balas Spitzer modernas. [27] Para obtener coeficientes de retardo relevantes para un modelado óptimo de largo alcance, el Dr. Pejsa sugirió utilizar datos precisos de medición de velocidad de proyectil específica a larga distancia para un proyectil en particular para derivar empíricamente el coeficiente de retardo promedio en lugar de utilizar un coeficiente de retardo promedio derivado de una curva de arrastre de referencia. Además, sugirió utilizar munición con cargas de propulsor reducidas para probar empíricamente el comportamiento real del vuelo del proyectil a velocidades más bajas. Cuando se trabaja con cargas de propulsor reducidas, se debe tener el máximo cuidado para evitar condiciones peligrosas o catastróficas (detonaciones) que pueden ocurrir al disparar cargas experimentales en armas de fuego. [21]
Modelo de Manges
Aunque no es tan conocido como el modelo Pejsa, en 1989 el coronel Duff Manges (retirado del ejército de los EE. UU.) presentó un modelo balístico alternativo adicional en el 11.º Simposio balístico internacional de preparación para la defensa estadounidense (ADPA), celebrado en el Centro de Congresos de Bruselas (Bélgica) del 9 al 11 de mayo de 1989. En las actas, volumen 1, dinámica de propulsión, dinámica de lanzamiento, dinámica de vuelo, páginas 665 a 674, aparece un artículo titulado "Closed Form Trajectory Solutions for Direct Fire Weapons Systems". Concebida originalmente para modelar la resistencia del proyectil para municiones de cañones de tanque de 120 mm , la novedosa fórmula del coeficiente de resistencia se ha aplicado posteriormente a las trayectorias balísticas de municiones de fusil de fuego central con resultados comparables a los que se afirman para el modelo Pejsa.
El modelo de Manges utiliza un enfoque teórico de principios básicos que evita las curvas "G" y los "coeficientes balísticos" basados en la G1 estándar y otras curvas de similitud. La descripción teórica tiene tres partes principales. La primera es desarrollar y resolver una formulación de las ecuaciones diferenciales de movimiento bidimensionales que rigen las trayectorias planas de proyectiles de masa puntual definiendo matemáticamente un conjunto de cuadraturas que permiten soluciones de forma cerrada para las ecuaciones diferenciales de movimiento de trayectoria. Se genera una secuencia de funciones de coeficientes de arrastre de aproximación sucesiva que convergen rápidamente a los datos de arrastre observados reales. Los modelos de trayectoria de vacío, aerodinámico simplificado, de d'Antonio y de ley de arrastre de Euler son casos especiales. La ley de arrastre de Manges proporciona así una influencia unificadora con respecto a los modelos anteriores utilizados para obtener soluciones de forma cerrada bidimensionales para las ecuaciones de movimiento de masa puntual. El tercer propósito de este artículo es describir un procedimiento de ajuste de mínimos cuadrados para obtener las nuevas funciones de arrastre a partir de datos experimentales observados. El autor afirma que los resultados muestran una excelente concordancia con los cálculos numéricos de seis grados de libertad para municiones de tanques modernos y las tablas de disparo publicadas disponibles para municiones de rifles de disparo central que tienen una amplia variedad de formas y tamaños.
Se ha creado una aplicación de Microsoft Excel que utiliza ajustes de mínimos cuadrados de los coeficientes de arrastre tabulares adquiridos en el túnel de viento. Alternativamente, también se pueden ajustar los datos de trayectoria balística proporcionados por el fabricante o los datos de velocidad adquiridos por Doppler para calibrar el modelo. Luego, la aplicación de Excel emplea macroinstrucciones personalizadas para calcular las variables de trayectoria de interés. Se utiliza un algoritmo de integración de Runge-Kutta de cuarto orden modificado . Al igual que Pejsa, el coronel Manges afirma que las precisiones de los rifles disparados al centro se sitúan en la décima de pulgada más cercana para la posición de la bala y en el pie por segundo más cercano para la velocidad del proyectil.
Las actas del 11º Simposio Balístico Internacional están disponibles a través de la Asociación Industrial de Defensa Nacional (NDIA) en el sitio web http://www.ndia.org/Resources/Pages/Publication_Catalog.aspx Archivado el 26 de enero de 2012 en Wayback Machine .
Modelo de seis grados de libertad
También hay modelos balísticos profesionales avanzados disponibles como PRODAS. Estos se basan en cálculos de seis grados de libertad (6 DoF). El modelado de 6 DoF tiene en cuenta la posición x, y, y z en el espacio junto con las velocidades de cabeceo, guiñada y alabeo de los proyectiles. El modelado de 6 DoF necesita una entrada de datos tan elaborada, conocimiento de los proyectiles empleados y métodos costosos de recopilación y verificación de datos que es poco práctico para balísticos no profesionales, [28] pero no imposible para los curiosos, con conocimientos de informática y con inclinación a las matemáticas. Se han desarrollado modelos de aeropredicción semiempíricos que redujeron los datos extensos del rango de prueba en una amplia variedad de formas de proyectiles, normalizando las geometrías de entrada dimensionales a calibres; teniendo en cuenta la longitud y el radio de la nariz, la longitud del cuerpo y el tamaño de la cola de barco, y permitiendo que se calcule el conjunto completo de coeficientes aerodinámicos de 6 dof. Las primeras investigaciones sobre el software de aeropredicción estabilizado por giro dieron como resultado el programa informático SPINNER. [29] El código de aeropredicción FINNER calcula entradas de 6 grados de libertad para proyectiles estabilizados por aletas. [30] El software de modelado de sólidos que determina los parámetros del proyectil de masa, centro de gravedad, momentos de inercia axial y transversal necesarios para el análisis de estabilidad también está disponible y es fácil de programar por computadora. [31] Finalmente, los algoritmos para la integración numérica de 6 grados de libertad adecuados para un Runge-Kutta de cuarto orden están fácilmente disponibles. [32] Todo lo que se requiere para que el balístico aficionado investigue los detalles analíticos más finos de las trayectorias de los proyectiles, junto con la nutación de la bala y el comportamiento de precesión , es la determinación de la programación de la computadora. Sin embargo, para el entusiasta de las armas pequeñas, además de la curiosidad académica, uno descubrirá que ser capaz de predecir trayectorias con una precisión de 6 grados de libertad probablemente no tenga importancia práctica en comparación con trayectorias de masa puntual más simplificadas basadas en coeficientes balísticos de bala publicados. El método de 6 DoF se utiliza generalmente en la industria aeroespacial y de defensa y en organizaciones militares que estudian el comportamiento balístico de un número limitado de proyectiles militares (previstos). Las tendencias de 6 DoF calculadas se pueden incorporar como tablas de corrección en aplicaciones de software balístico más convencionales.
Aunque las organizaciones profesionales bien equipadas llevan décadas utilizando modelos y aplicaciones de software de 6 DoF, las restricciones de potencia informática de los dispositivos informáticos móviles, como los asistentes digitales personales (reforzados) , las tabletas o los teléfonos inteligentes, han dificultado su uso en el campo, ya que los cálculos generalmente deben realizarse sobre la marcha. En 2016, el fabricante de municiones escandinavo Nammo Lapua Oy lanzó un software balístico gratuito basado en un modelo de cálculo de 6 DoF llamado Lapua Ballistics. El software se distribuye solo como una aplicación móvil y está disponible para dispositivos Android e iOS. [33] Sin embargo, el modelo de 6 DoF empleado está limitado a las balas Lapua, ya que un solucionador de 6 DoF necesita datos de coeficiente de arrastre (Cd)/radar Doppler específicos de la bala y dimensiones geométricas del proyectil o proyectiles de interés. Para otras balas, el solucionador Lapua Ballistics está limitado y se basa en coeficientes balísticos G1 o G7 y el método Mayevski/Siacci.
Paquetes de software de artillería
Las organizaciones militares han desarrollado modelos balísticos como el NATO Armament Ballistic Kernel (NABK) para sistemas de control de fuego para artillería como el SG2 Shareable (Fire Control) Software Suite (S4) del NATO Army Armaments Group (NAAG). El NATO Armament Ballistic Kernel es un modelo de masa puntual modificado de 4 DoF. Se trata de un compromiso entre un modelo de masa puntual simple y un modelo de 6 DoF computacionalmente intensivo. [34] También se ha desarrollado un estándar de seis y siete grados de libertad llamado BALCO dentro de los grupos de trabajo de la OTAN. BALCO es un programa de simulación de trayectorias basado en el modelo matemático definido por la Recomendación de Normalización 4618 de la OTAN. El objetivo principal de BALCO es calcular trayectorias de alta fidelidad tanto para proyectiles axisimétricos convencionales como para proyectiles guiados con precisión que presentan superficies de control. El modelo de trayectoria BALCO es un programa FORTRAN 2003 que implementa las siguientes características:
- Ecuaciones de movimiento de 6/7 grados de libertad
- Integración de Runge-Kutta-Fehlberg de séptimo orden
- Modelos de la Tierra
- Modelos atmosféricos
- Modelos aerodinámicos
- Modelos de empuje y quema de base
- Modelos de actuadores [35]
Las predicciones que estos modelos producen están sujetas a estudios comparativos. [36]
Mediciones de radar Doppler
Para determinar con precisión los efectos de la resistencia del aire o del arrastre sobre los proyectiles, se requieren mediciones con radar Doppler . Los radares Doppler Weibel 1000e o Infinition BR-1001 son utilizados por gobiernos, balistas profesionales, fuerzas de defensa y algunos fabricantes de municiones para obtener datos reales del comportamiento de vuelo de los proyectiles de su interés. Las mediciones con radar Doppler de última generación correctamente establecidas pueden determinar el comportamiento de vuelo de proyectiles tan pequeños como perdigones de pistolas de aire comprimido en un espacio tridimensional con una precisión de unos pocos milímetros. Los datos recopilados sobre la desaceleración del proyectil se pueden derivar y expresar de varias maneras, como coeficientes balísticos (BC) o coeficientes de arrastre (C d ). Debido a que un proyectil giratorio experimenta tanto precesión como nutación sobre su centro de gravedad mientras vuela, se requiere una mayor reducción de datos de las mediciones con radar Doppler para separar los coeficientes de arrastre y sustentación inducidos por la guiñada del coeficiente de arrastre de guiñada cero, a fin de que las mediciones sean totalmente aplicables al análisis de trayectorias de 6 grados de libertad.
Los resultados de la medición del radar Doppler para una bala sólida monolítica de calibre .50 BMG torneada en torno con muy baja resistencia (bala sólida monolítica Lost River J40 de grano .510-773 / velocidad de torsión de 1:15 pulgadas) se ven así:
| Alcance (m) | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | 1200 | 1300 | 1400 | 1500 | 1600 | 1700 | 1800 | 1900 | 2000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coeficiente balístico | 1.040 | 1.051 | 1.057 | 1.063 | 1.064 | 1.067 | 1.068 | 1.068 | 1.068 | 1.066 | 1.064 | 1.060 | 1.056 | 1.050 | 1.042 | 1.032 |
El aumento inicial del valor BC se atribuye a la constante oscilación y precesión del proyectil al salir del cañón. Los resultados de la prueba se obtuvieron de muchos disparos, no de un solo disparo. El fabricante de la bala, Lost River Ballistic Technologies, le asignó a la bala un número BC de 1,062.
Los resultados de la medición del radar Doppler para una bala de muy baja resistencia Lapua GB528 Scenar de calibre 19,44 g (300 gr) y 8,59 mm (0,338 pulgadas) se ven así:
| Número de Mach | 0.000 | 0.400 | 0,500 | 0.600 | 0,700 | 0.800 | 0,825 | 0,850 | 0,875 | 0.900 | 0,925 | 0,950 | 0,975 | 1.000 | 1.025 | 1.050 | 1.075 | 1.100 | 1.150 | 1.200 | 1.300 | 1.400 | 1.500 | 1.600 | 1.800 | 2.000 | 2.200 | 2.400 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coeficiente de arrastre | 0,230 | 0,229 | 0,200 | 0,171 | 0,164 | 0,144 | 0,141 | 0,137 | 0,137 | 0,142 | 0,154 | 0,177 | 0,236 | 0,306 | 0,334 | 0,341 | 0,345 | 0,347 | 0,348 | 0,348 | 0,343 | 0,336 | 0,328 | 0,321 | 0,304 | 0,292 | 0,282 | 0,270 |
Esta bala probada experimenta su máximo coeficiente de arrastre al entrar en el régimen de vuelo transónico alrededor de Mach 1.200.
Con la ayuda de las mediciones del radar Doppler se pueden establecer modelos específicos de la resistencia al avance del proyectil, que son más útiles cuando se dispara a distancias extensas, donde la velocidad de la bala se reduce hasta la región de velocidad transónica, cerca de la velocidad del sonido. Aquí es donde la resistencia al avance del proyectil predicha por el modelo matemático puede diferir significativamente de la resistencia al avance real que experimenta el proyectil. Otras mediciones del radar Doppler se utilizan para estudiar los sutiles efectos en vuelo de varias construcciones de balas. [37]
Los gobiernos, los balísticos profesionales, las fuerzas de defensa y los fabricantes de municiones pueden complementar las mediciones del radar Doppler con mediciones obtenidas mediante sondas de telemetría instaladas en proyectiles más grandes.
Tendencias generales en el coeficiente balístico o de arrastre

En general, un proyectil puntiagudo tendrá un mejor coeficiente de arrastre (C d ) o coeficiente balístico (BC) que una bala de punta redonda, y una bala de punta redonda tendrá un mejor C d o BC que una bala de punta plana. Las curvas de radio grande, que resultan en un ángulo de punta menos profundo, producirán arrastres menores, particularmente a velocidades supersónicas. Las balas de punta hueca se comportan de manera muy similar a una punta plana del mismo diámetro de punta. Los proyectiles diseñados para uso supersónico a menudo tienen una base ligeramente cónica en la parte trasera, llamada cola de barco , que reduce la resistencia del aire en vuelo. [38] La utilidad de una "parte trasera cónica" para disparos de largo alcance ya estaba bien establecida a principios de la década de 1870, [39] pero las dificultades tecnológicas impidieron su amplia adopción antes de bien entrado el siglo XX. Las caneluras , que son anillos empotrados alrededor del proyectil que se utilizan para engarzar el proyectil de forma segura en la vaina, provocarán un aumento en la resistencia.
El Laboratorio de Investigación Balística (posteriormente llamado Laboratorio de Investigación del Ejército ) desarrolló un software analítico que redujo los datos reales del rango de prueba a relaciones paramétricas para la predicción del coeficiente de arrastre del proyectil. [40] La artillería de gran calibre también emplea mecanismos de reducción de arrastre además de una geometría aerodinámica. Los proyectiles asistidos por cohetes emplean un pequeño motor de cohete que se enciende al salir de la boca del cañón, proporcionando un empuje adicional para superar la resistencia aerodinámica. La asistencia por cohetes es más efectiva con proyectiles de artillería subsónica. Para la artillería supersónica de largo alcance, donde domina la resistencia de base, se emplea el sangrado de base . El sangrado de base es una forma de generador de gas que no proporciona un empuje significativo, sino que llena el área de baja presión detrás del proyectil con gas, reduciendo efectivamente la resistencia de base y el coeficiente de arrastre general del proyectil.
Problema transónico
Un proyectil disparado a una velocidad inicial supersónica en algún momento se desacelerará hasta aproximarse a la velocidad del sonido. En la región transónica (alrededor de Mach 1,2-0,8), el centro de presión (CP) de la mayoría de los proyectiles no esféricos se desplaza hacia adelante a medida que el proyectil desacelera. Ese cambio de CP afecta la estabilidad (dinámica) del proyectil. Si el proyectil no está bien estabilizado, no puede permanecer apuntando hacia adelante a través de la región transónica (el proyectil comienza a exhibir una precesión no deseada o un movimiento de conificación llamado guiñada de ciclo límite que, si no se amortigua, puede terminar eventualmente en un volteo incontrolable a lo largo del eje de longitud). Sin embargo, incluso si el proyectil tiene suficiente estabilidad (estática y dinámica) para poder volar a través de la región transónica y permanece apuntando hacia adelante, aún se ve afectado. El cambio errático y repentino de CP y la disminución (temporal) de la estabilidad dinámica pueden causar una dispersión significativa (y, por lo tanto, una disminución significativa de la precisión), incluso si el vuelo del proyectil se comporta bien nuevamente cuando ingresa a la región subsónica . Esto hace que sea muy difícil predecir con precisión el comportamiento balístico de los proyectiles en la región transónica.
Por este motivo, los tiradores normalmente se limitan a disparar a objetivos lo suficientemente cercanos como para que el proyectil siga siendo supersónico. [nota 1] En 2015, el balístico estadounidense Bryan Litz introdujo el concepto de "largo alcance extendido" para definir el tiro con rifle en rangos en los que las balas (de rifle) disparadas a velocidades supersónicas entran en la región transónica. Según Litz, "el largo alcance extendido comienza cuando la bala reduce su velocidad hasta alcanzar su rango transónico. A medida que la bala reduce su velocidad para acercarse a Mach 1, comienza a encontrar efectos transónicos, que son más complejos y difíciles de explicar, en comparación con el rango supersónico, donde la bala se comporta relativamente bien". [41]
La densidad del aire ambiente tiene un efecto significativo en la estabilidad dinámica durante la transición transónica. Aunque la densidad del aire ambiente es un factor ambiental variable, los efectos adversos de la transición transónica se pueden anular mejor con un proyectil que viaja a través de aire menos denso que cuando viaja a través de aire más denso. La longitud del proyectil o la bala también afecta la guiñada del ciclo límite. Los proyectiles más largos experimentan más guiñada del ciclo límite que los proyectiles más cortos del mismo diámetro. Otra característica del diseño del proyectil que se ha identificado como que tiene un efecto en el movimiento de guiñada del ciclo límite no deseado es el chaflán en la base del proyectil. En la base misma, o talón de un proyectil o bala, hay un chaflán o radio de 0,25 a 0,50 mm (0,01 a 0,02 pulgadas). La presencia de este radio hace que el proyectil vuele con mayores ángulos de guiñada del ciclo límite. [42] El estriado también puede tener un efecto sutil en la guiñada del ciclo límite. [43] En general, los proyectiles que giran más rápido experimentan menos guiñada del ciclo límite.
Investigación sobre proyectiles guiados
Para evitar los problemas transónicos que presentan los proyectiles estabilizados por giro, teóricamente se pueden guiar durante el vuelo. Los Laboratorios Nacionales Sandia anunciaron en enero de 2012 que habían investigado y probado un prototipo de balas autoguiadas de 102 mm (4 pulgadas) de largo, similares a dardos, para armas de fuego de pequeño calibre y de ánima lisa, que podían alcanzar objetivos designados por láser a distancias de más de una milla (unos 1.610 metros o 1.760 yardas). Estos proyectiles no están estabilizados por giro y la trayectoria de vuelo se puede dirigir dentro de ciertos límites con un actuador electromagnético 30 veces por segundo. Los investigadores también afirman que tienen un vídeo de la bala que se inclina radicalmente al salir del cañón y se inclina menos al volar a larga distancia, un fenómeno controvertido conocido por los expertos en armas de fuego de largo alcance como "dormir". Debido a que los movimientos de la bala se estabilizan cuanto más tiempo está en vuelo, la precisión mejora a distancias mayores, dijo el investigador de Sandia, Red Jones. “Nadie había visto eso nunca, pero tenemos fotografías de video de alta velocidad que muestran que es verdad”, dijo. [44] Pruebas recientes indican que podría estar acercándose o ya haber alcanzado su capacidad operativa inicial. [45]
Poniendo a prueba las cualidades predictivas del software
Debido a la imposibilidad práctica de conocer de antemano y compensar todas las variables del vuelo, ningún software de simulación, por avanzado que sea, proporcionará predicciones que siempre coincidan perfectamente con las trayectorias del mundo real. Sin embargo, es posible obtener predicciones que se aproximen mucho al comportamiento real del vuelo.
Método de medición empírico
Los programas informáticos de predicción balística diseñados para distancias (extremadamente) largas pueden evaluarse realizando pruebas de campo en el rango de transición supersónico a subsónico (el último 10 a 20% del rango supersónico de la combinación rifle/cartucho/bala). Por ejemplo, para un rifle Lapua Magnum .338 típico, que dispara balas estándar Lapua Scenar GB488 de 16,2 gramos (250 gr) a una velocidad inicial de 905 m/s (2969 ft/s), las pruebas de campo del software deben realizarse a ≈ 1200-1300 metros (1312-1422 yd) en condiciones atmosféricas estándar internacionales a nivel del mar ( densidad del aire ρ = 1,225 kg/m³). Para verificar qué tan bien el software predice la trayectoria a distancias cortas a medias, deben realizarse pruebas de campo al 20, 40 y 60% del rango supersónico. En esas distancias cortas a medias, no deberían ocurrir problemas transónicos y, por lo tanto, vuelo de bala no controlado, y es menos probable que el BC sea transitorio. Probar las cualidades predictivas del software en distancias (extremadamente) largas es costoso porque consume munición; se debe medir la velocidad inicial real de todos los disparos para poder hacer afirmaciones estadísticamente confiables. Los grupos de muestra de menos de 24 disparos pueden no obtener el intervalo de confianza estadísticamente significativo deseado .
Método de medición por radar Doppler
Los gobiernos, los balísticos profesionales, las fuerzas de defensa y algunos fabricantes de municiones utilizan radares Doppler y/o sondas de telemetría instaladas en proyectiles más grandes para obtener datos precisos del mundo real sobre el comportamiento de vuelo de los proyectiles específicos de su interés y, a continuación, comparar los datos del mundo real recopilados con las predicciones calculadas por programas informáticos balísticos. Sin embargo, el aficionado normal al tiro o a la aerodinámica no tiene acceso a dispositivos de medición profesionales tan caros. Las autoridades y los fabricantes de proyectiles generalmente se muestran reacios a compartir los resultados de las pruebas de radar Doppler y los coeficientes de arrastre derivados de las pruebas (C d ) de los proyectiles con el público en general. Alrededor de 2020, se puso a disposición del público en general un equipo de radar Doppler más asequible pero menos capaz (para aficionados) para determinar los coeficientes de arrastre en vuelo libre. [46]
En enero de 2009, el fabricante de municiones escandinavo Nammo/Lapua publicó datos de coeficiente de arrastre derivados de pruebas de radar Doppler para la mayoría de sus proyectiles de rifle. [47] [48] En 2015, el fabricante de municiones estadounidense Berger Bullets anunció el uso del radar Doppler al unísono con el software PRODAS 6 DoF para generar soluciones de trayectoria. [49] En 2016, el fabricante de municiones estadounidense Hornady anunció el uso de datos de arrastre derivados del radar Doppler en software que utiliza un modelo de masa puntual modificado para generar soluciones de trayectoria. [50] [51] [52] [53] Con los datos de C d derivados de la medición , los ingenieros pueden crear algoritmos que utilicen tanto modelos balísticos matemáticos conocidos como datos tabulares específicos de la prueba al unísono. Cuando se utilizan con software predictivo como QuickTARGET Unlimited , Lapua Edition, [54] Lapua Ballistics [55] o Hornady 4DOF, los datos del coeficiente de arrastre derivados de la prueba del radar Doppler se pueden utilizar para realizar predicciones balísticas externas más precisas.
Algunos de los datos de coeficiente de arrastre proporcionados por Lapua muestran aumentos drásticos en el arrastre medido alrededor o por debajo de la región de velocidad de vuelo de Mach 1. Este comportamiento se observó para la mayoría de las balas de pequeño calibre medidas, y no tanto para las balas de mayor calibre. Esto implica que algunas balas de fusil (en su mayoría de menor calibre) exhibieron más guiñada de ciclo límite (conificación y/o volteo) en el régimen de velocidad de vuelo transónico/subsónico. La información sobre el comportamiento desfavorable de vuelo transónico/subsónico para algunos de los proyectiles probados es importante. Este es un factor limitante para el uso en tiro de largo alcance, porque los efectos de la guiñada de ciclo límite no son fácilmente predecibles y potencialmente catastróficos para los mejores modelos y software de predicción balística.
Los datos de C d presentados no se pueden utilizar simplemente para cada combinación de arma y munición, ya que se midieron para los cañones, las velocidades de rotación (giro) y los lotes de munición que los probadores de Lapua usaron durante sus disparos de prueba. Variables como las diferencias en el estriado (número de ranuras, profundidad, ancho y otras propiedades dimensionales), las velocidades de torsión y/o las velocidades iniciales imparten diferentes velocidades de rotación (giro) y marcas de estriado en los proyectiles. Los cambios en dichas variables y las variaciones en los lotes de producción de proyectiles pueden producir diferentes interacciones a distancia con el aire por el que pasa el proyectil, lo que puede dar lugar a cambios (menores) en el comportamiento de vuelo. Este campo particular de la balística externa actualmente (2009) no se ha estudiado en profundidad ni se comprende bien. [56]
Predicciones de varios métodos de medición y modelado de resistencia al arrastre
El método empleado para modelar y predecir el comportamiento balístico externo puede arrojar resultados diferentes con un aumento del alcance y el tiempo de vuelo. Para ilustrar esto, varios métodos de predicción del comportamiento balístico externo para la bala de fusil Lapua Scenar GB528 de 19,44 g (300 gr) de calibre 8,59 mm (0,338 in) de muy baja resistencia con un coeficiente balístico G1 (BC) indicado por el fabricante de 0,785 disparada a una velocidad inicial de 830 m/s (2723 ft/s) en condiciones atmosféricas estándar internacionales a nivel del mar ( densidad del aire ρ = 1,225 kg/m³), Mach 1 = 340,3 m/s, Mach 1,2 = 408,4 m/s), predijeron esto para la velocidad del proyectil y el tiempo de vuelo de 0 a 3000 m (0 a 3281 yd): [nota 2]
| Alcance (m) | 0 | 300 | 600 | 900 | 1.200 | 1.500 | 1.800 | 2.100 | 2.400 | 2.700 | 3.000 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Método de coeficientes de arrastre derivados de pruebas de radar V (m/s) | 830 | 711 | 604 | 507 | 422 | 349 | 311 | 288 | 267 | 247 | 227 |
| Tiempo de vuelo(s) | 0.0000 | 0,3918 | 0,8507 | 1.3937 | 2.0435 | 2.8276 | 3.7480 | 4.7522 | 5.8354 | 7.0095 | 8.2909 |
| Caída total (m) | 0.000 | 0,715 | 3.203 | 8.146 | 16.571 | 30.035 | 50.715 | 80.529 | 121.023 | 173.998 | 241.735 |
| Método de modelado de 6 DoF V (m/s) | 830 | 711 | 604 | 506 | 420 | 347 | 310 | 287 | 266 | 244 | 222 |
| Tiempo de vuelo(s) | 0.0000 | 0,3919 | 0,8511 | 1.3949 | 2.0467 | 2.8343 | 3.7575 | 4.7641 | 5.8508 | 7.0332 | 8.3346 |
| Caída total (m) | 0.000 | 0,714 | 3.195 | 8.132 | 16.561 | 30.060 | 50.836 | 80.794 | 121.498 | 174.796 | 243.191 |
| Método del modelo de arrastre G1 V (m/s) | 830 | 718 | 615 | 522 | 440 | 374 | 328 | 299 | 278 | 261 | 248 |
| Tiempo de vuelo(s) | 0.0000 | 0,3897 | 0,8423 | 1.3732 | 2.0009 | 2.7427 | 3.6029 | 4.5642 | 5.6086 | 6.7276 | 7.9183 |
| Caída total (m) | 0.000 | 0,710 | 3.157 | 7.971 | 16.073 | 28.779 | 47.810 | 75.205 | 112.136 | 160.739 | 222.430 |
| Método del modelo de arrastre de Pejsa V (m/s) | 830 | 712 | 603 | 504 | 413 | 339 | 297 | 270 | 247 | 227 | 208 |
| Tiempo de vuelo(s) | 0.0000 | 0,3902 | 0,8479 | 1.3921 | 2.0501 | 2.8556 | 3.8057 | 4.8682 | 6.0294 | 7.2958 | 8.6769 |
| Caída total (m) | 0.000 | 0,719 | 3.198 | 8.129 | 16.580 | 30.271 | 51.582 | 82.873 | 126.870 | 185.318 | 260.968 |
| Método del modelo de arrastre G7 V (m/s) | 830 | 713 | 606 | 508 | 418 | 339 | 303 | 283 | 265 | 249 | 235 |
| Tiempo de vuelo(s) | 0.0000 | 0,3912 | 0,8487 | 1.3901 | 2.0415 | 2.8404 | 3.7850 | 4.8110 | 5.9099 | 7.0838 | 8.3369 |
| Caída total (m) | 0.000 | 0,714 | 3.191 | 8.109 | 16.503 | 30.039 | 51.165 | 81.863 | 123.639 | 178.082 | 246.968 |
La tabla muestra que el método de predicción de los coeficientes de arrastre derivados de la prueba del radar Doppler (C d ) y las predicciones de la aplicación Lapua Ballistics 6 DoF de 2017 producen resultados similares. El modelo de 6 DoF estima la estabilidad de la bala ((S d ) y (S g )) que gravita hacia la sobreestabilización para rangos superiores a 2400 m (2625 yd) para esta bala. A 2400 m (2625 yd) las predicciones de caída total se desvían 47,5 cm (19,7 in) o 0,20 mil (0,68 moa ) a 50° de latitud y hasta 2700 m (2953 yd) las predicciones de caída total están dentro de 0,30 mil (1 moa) a 50° de latitud. Las predicciones de la versión 2016 de la aplicación Lapua Ballistics 6 DoF fueron incluso más cercanas a las predicciones de la prueba del radar Doppler.
El método tradicional de predicción de la curva de arrastre del modelo G1 de Siacci/Mayevski generalmente produce resultados más optimistas en comparación con el método moderno de predicción de coeficientes de arrastre derivados de la prueba del radar Doppler (C d ). [nota 3] A un alcance de 300 m (328 yd) las diferencias serán apenas perceptibles, pero a 600 m (656 yd) y más allá las diferencias crecen sobre una velocidad de proyectil de 10 m/s (32,8 ft/s) y gradualmente se vuelven significativas. A un alcance de 1.500 m (1.640 yd) las predicciones de la velocidad del proyectil se desvían 25 m/s (82,0 ft/s), lo que equivale a una diferencia de caída total prevista de 125,6 cm (49,4 in) o 0,83 mil (2,87 moa) a 50° de latitud.
El método de predicción de la solución de forma cerrada del modelo de arrastre de Pejsa, sin ajuste fino del factor de constante de pendiente, arroja resultados muy similares en el régimen de vuelo supersónico en comparación con el método de predicción de coeficientes de arrastre derivados de la prueba del radar Doppler (C d ). A un alcance de 1500 m (1640 yd), las predicciones de velocidad del proyectil se desvían 10 m/s (32,8 ft/s), lo que equivale a una diferencia de caída total prevista de 23,6 cm (9,3 in) o 0,16 mil (0,54 moa) a 50° de latitud.
El método de predicción del modelo de curva de arrastre G7 (recomendado por algunos fabricantes para balas de fusil con forma de muy baja resistencia) cuando se utiliza un coeficiente balístico G7 (BC) de 0,377 arroja resultados muy similares en el régimen de vuelo supersónico en comparación con el método de predicción de coeficientes de arrastre derivados de la prueba del radar Doppler (C d ). A un alcance de 1500 m (1640 yd), las predicciones de velocidad del proyectil tienen su desviación máxima de 10 m/s (32,8 ft/s). La diferencia de caída total prevista a 1500 m (1640 yd) es de 0,4 cm (0,16 in) a 50° de latitud. La diferencia de caída total prevista a 1800 m (1969 yd) es de 45,0 cm (17,7 in), lo que equivale a 0,25 mil (0,86 moa).
Se espera que los modelos de predicción decentes arrojen resultados similares en el régimen de vuelo supersónico. Los cinco modelos de ejemplo hasta 1200 m (1312 yd) predicen velocidades de proyectiles supersónicas de Mach 1,2+ y diferencias totales de caída dentro de un ancho de banda de 51 cm (20,1 in). En el régimen de vuelo transónico a 1500 m (1640 yd), los modelos predicen velocidades de proyectiles de alrededor de Mach 1,0 a Mach 1,1 y diferencias totales de caída dentro de un ancho de banda mucho mayor de 150 cm (59 in).
Factores externos
Viento
El viento tiene una serie de efectos, el primero de los cuales es el de hacer que el proyectil se desvíe hacia un lado (desviación horizontal). Desde una perspectiva científica, el "viento que empuja hacia un lado del proyectil" no es lo que causa la desviación horizontal del viento. Lo que causa la desviación del viento es la resistencia. La resistencia hace que el proyectil gire hacia el viento, de forma muy similar a una veleta, manteniendo el centro de la presión del aire en su punta. Desde la perspectiva del tirador, esto hace que la punta del proyectil gire hacia el viento y la cola se aleje del viento. El resultado de este efecto de giro es que la resistencia empuja el proyectil a favor del viento en una dirección de punta a cola.
El viento también causa un salto aerodinámico, que es el componente vertical de la desviación del viento cruzado causado por los impulsos laterales (del viento) activados durante el vuelo libre de un proyectil o en la boca del cañón o muy cerca de ella, lo que provoca un desequilibrio dinámico. [57] La cantidad de salto aerodinámico depende de la velocidad del viento cruzado, la estabilidad giroscópica de la bala en la boca del cañón y si el giro del cañón es en el sentido de las agujas del reloj o en sentido contrario. Al igual que la dirección del viento, invertir la dirección del giro invertirá la dirección del salto aerodinámico.
Un efecto menos obvio es el causado por los vientos de frente o de cola. Un viento de frente aumentará ligeramente la velocidad relativa del proyectil y aumentará la resistencia y la caída correspondiente. Un viento de cola reducirá la resistencia y la caída del proyectil o la bala. En el mundo real, los vientos de frente o de cola puros son poco frecuentes, ya que el viento rara vez tiene una fuerza y una dirección constantes y normalmente interactúa con el terreno sobre el que sopla. Esto a menudo dificulta los disparos a distancias ultralargas en condiciones de viento de frente o de cola.
Ángulos verticales
El ángulo vertical (o elevación ) de un disparo también afectará la trayectoria del mismo. Las tablas balísticas para proyectiles de pequeño calibre (disparados desde pistolas o rifles) suponen una línea de visión horizontal entre el tirador y el objetivo con la gravedad actuando perpendicularmente a la tierra. Por lo tanto, si el ángulo tirador-objetivo es hacia arriba o hacia abajo (la dirección del componente de gravedad no cambia con la dirección de la pendiente), entonces la aceleración de curvatura de la trayectoria debido a la gravedad será en realidad menor, en proporción al coseno del ángulo de inclinación. Como resultado, un proyectil disparado hacia arriba o hacia abajo, en un llamado "rango de inclinación", sobrepasará la misma distancia del objetivo en terreno llano. El efecto es de suficiente magnitud como para que los cazadores deban ajustar su distancia de tiro en consecuencia en terreno montañoso. Una fórmula bien conocida para el ajuste del rango de inclinación a la distancia de tiro horizontal se conoce como la regla del tirador . La regla del tirador y los modelos de la regla del tirador mejorada, ligeramente más complejos y menos conocidos, producen predicciones suficientemente precisas para muchas aplicaciones de armas pequeñas. Sin embargo, los modelos de predicción simples ignoran los efectos menores de la gravedad al disparar cuesta arriba o cuesta abajo. La única forma práctica de compensar esto es usar un programa informático balístico. Además de la gravedad en ángulos muy pronunciados a largas distancias, el efecto de los cambios de densidad del aire en los encuentros de proyectiles durante el vuelo se vuelve problemático. [58] Los modelos de predicción matemática disponibles para escenarios de fuego inclinado, dependiendo de la cantidad y dirección (cuesta arriba o cuesta abajo) del ángulo de inclinación y el alcance, producen diferentes niveles de expectativa de precisión. [59] Los programas informáticos balísticos menos avanzados predicen la misma trayectoria para disparos cuesta arriba y cuesta abajo en el mismo ángulo vertical y alcance. Los programas más avanzados tienen en cuenta el pequeño efecto de la gravedad en los disparos cuesta arriba y cuesta abajo, lo que resulta en trayectorias ligeramente diferentes en el mismo ángulo vertical y alcance. Ningún programa informático balístico disponible públicamente actualmente (2017) da cuenta de los complicados fenómenos de las diferentes densidades del aire que encuentra el proyectil durante el vuelo.
Densidad del aire ambiente
Las variaciones de presión del aire , temperatura y humedad conforman la densidad del aire ambiente . La humedad tiene un efecto contrario a lo que parece intuitivo. Dado que el vapor de agua tiene una densidad de 0,8 gramos por litro, mientras que el aire seco tiene una media de unos 1,225 gramos por litro, una mayor humedad en realidad reduce la densidad del aire y, por tanto, la resistencia aerodinámica.
Precipitación
La precipitación puede provocar un importante desvío y desviación cuando una bala choca con una gota de lluvia. Cuanto más lejos se produzca una colisión casual, menor será la desviación hacia el objetivo. El peso de la gota de lluvia y de la bala también influye en la desviación que se produce durante una colisión de este tipo. Una gota de lluvia grande y pesada y una bala ligera producirán el máximo efecto de desviación. Una bala pesada que choque con una gota de lluvia de igual tamaño experimentará un efecto de desviación significativamente menor. [60]
Factores de largo alcance
Deriva giroscópica (deriva de giro)
La deriva giroscópica es una interacción de la masa y la aerodinámica de la bala con la atmósfera en la que vuela. Incluso en aire completamente calmado, sin movimiento lateral de aire en absoluto, un proyectil estabilizado por giro experimentará un componente lateral inducido por el giro, debido a un fenómeno giroscópico conocido como "guiñada de reposo". Para una dirección de rotación hacia la derecha (en el sentido de las agujas del reloj), este componente siempre será hacia la derecha. Para una dirección de rotación hacia la izquierda (en el sentido contrario a las agujas del reloj), este componente siempre será hacia la izquierda. Esto se debe a que el eje longitudinal del proyectil (su eje de rotación) y la dirección del vector de velocidad del centro de gravedad (CG) se desvían en un ángulo pequeño, que se dice que es la guiñada de equilibrio o la guiñada de reposo. La magnitud del ángulo de guiñada de reposo es típicamente menor a 0,5 grados. [61] Dado que los objetos giratorios reaccionan con un vector de velocidad angular de 90 grados del vector de torsión aplicado, el eje de simetría de la bala se mueve con un componente en el plano vertical y un componente en el plano horizontal; En el caso de balas que giran hacia la derecha (en el sentido de las agujas del reloj), el eje de simetría de la bala se desvía hacia la derecha y un poco hacia arriba con respecto a la dirección del vector de velocidad, a medida que el proyectil se mueve a lo largo de su arco balístico. Como resultado de esta pequeña inclinación, existe una corriente de aire continua, que tiende a desviar la bala hacia la derecha. Por lo tanto, la aparición de la desviación de reposo es la razón por la que la bala se desvía hacia la derecha (para el giro hacia la derecha) o hacia la izquierda (para el giro hacia la izquierda). Esto significa que la bala está "derrapando" lateralmente en un momento dado y, por lo tanto, experimenta un componente lateral. [62] [63]
Las siguientes variables afectan la magnitud de la deriva giroscópica:
- Longitud del proyectil o bala: los proyectiles más largos experimentan mayor deriva giroscópica porque producen mayor "elevación" lateral para un ángulo de guiñada determinado.
- Velocidad de giro: velocidades de giro más rápidas producirán más deriva giroscópica porque la nariz termina apuntando más hacia el lado.
- Alcance, tiempo de vuelo y altura de la trayectoria: la deriva giroscópica aumenta con todas estas variables.
- densidad de la atmósfera: un aire más denso aumentará la deriva giroscópica.
Los resultados de las mediciones del radar Doppler para la deriva giroscópica de varias balas militares estadounidenses y otras de muy baja resistencia a 1000 yardas (914,4 m) se ven así:
| Tipo de bala | Cañón M193 Ball (5,56 × 45 mm OTAN) del ejército estadounidense | Cañón especial M118 del ejército estadounidense (7,62 × 51 mm OTAN) | Palma Sierra MatchKing | Partido LRBT J40 | Sierra MatchKing | Sierra MatchKing | Partido LRBT J40 | Partido LRBT J40 |
|---|---|---|---|---|---|---|---|---|
| Masa del proyectil (en granos y g) | 55 granos (3,56 g) | 173 granos (11,21 g) | 155 granos (10,04 g) | 190 granos (12,31 g) | 220 granos (14,26 g) | 300 granos (19,44 g) | 350 granos (22,68 g) | 419 granos (27,15 g) |
| Diámetro del proyectil (en pulgadas y mm) | .224 pulgadas (5,69 mm) | .308 pulgadas (7,82 mm) | .308 pulgadas (7,82 mm) | .308 pulgadas (7,82 mm) | .308 pulgadas (7,82 mm) | .338 pulgadas (8,59 mm) | .375 pulgadas (9,53 mm) | .408 pulgadas (10,36 mm) |
| Deriva giroscópica (en pulgadas y mm) | 23,00 pulgadas (584,20 mm) | 11,50 pulgadas (292,10 mm) | 12,75 pulgadas (323,85 mm) | 3,00 pulgadas (76,20 mm) | 7,75 pulgadas (196,85 mm) | 6,50 pulgadas (165,10 mm) | 0,87 pulgadas (22,10 mm) | 1,90 pulgadas (48,26 mm) |
La tabla muestra que la deriva giroscópica no se puede predecir basándose únicamente en el peso y el diámetro. Para hacer predicciones precisas sobre la deriva giroscópica, se deben considerar varios detalles sobre la balística externa e interna. Factores como la velocidad de giro del cañón, la velocidad del proyectil cuando sale de la boca del cañón, los armónicos del cañón y las condiciones atmosféricas contribuyen a la trayectoria de un proyectil.
Efecto magnus
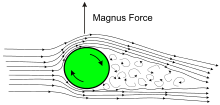
Los proyectiles estabilizados por giro se ven afectados por el efecto Magnus , por el cual el giro de la bala crea una fuerza que actúa hacia arriba o hacia abajo, perpendicular al vector lateral del viento. En el caso simple del viento horizontal y una dirección de rotación hacia la derecha (en el sentido de las agujas del reloj), las diferencias de presión inducidas por el efecto Magnus alrededor de la bala causan una fuerza hacia abajo (viento desde la derecha) o hacia arriba (viento desde la izquierda) vista desde el punto de disparo que actúa sobre el proyectil, afectando su punto de impacto. [64] El valor de la deflexión vertical tiende a ser pequeño en comparación con el componente de deflexión inducida por el viento horizontal, pero sin embargo puede ser significativo en vientos que superan los 4 m/s (14,4 km/h o 9 mph).
Efecto Magnus y estabilidad de la bala
El efecto Magnus tiene un papel importante en la estabilidad de la bala porque la fuerza Magnus no actúa sobre el centro de gravedad de la bala, sino sobre el centro de presión que afecta a la guiñada de la bala. El efecto Magnus actuará como una fuerza desestabilizadora sobre cualquier bala con un centro de presión situado por delante del centro de gravedad, mientras que, a la inversa, actuará como una fuerza estabilizadora sobre cualquier bala con el centro de presión situado detrás del centro de gravedad. La ubicación del centro de presión depende de la estructura del campo de flujo, en otras palabras, depende de si la bala está en vuelo supersónico, transónico o subsónico. Lo que esto significa en la práctica depende de la forma y otros atributos de la bala; en cualquier caso, la fuerza Magnus afecta en gran medida a la estabilidad porque intenta "torcer" la bala a lo largo de su trayectoria de vuelo. [65] [66]
Paradójicamente, las balas con muy baja resistencia al avance, debido a su longitud, tienen una tendencia a presentar mayores errores de desestabilización Magnus porque tienen una mayor área de superficie que presentar al aire que se aproxima por el que viajan, lo que reduce su eficiencia aerodinámica. Este efecto sutil es una de las razones por las que un C d o BC calculado en función de la forma y la densidad seccional es de uso limitado.
Efecto Poisson
Otra causa menor de deriva, que depende de que la punta del proyectil esté por encima de la trayectoria, es el efecto Poisson. Este, si se produce, actúa en la misma dirección que la deriva giroscópica y es incluso menos importante que el efecto Magnus. Supone que la punta inclinada del proyectil hace que se acumule un colchón de aire debajo de él. Supone además que hay un aumento de fricción entre este colchón y el proyectil, de modo que este último, con su giro, tenderá a rodar fuera del colchón y a moverse lateralmente.
Esta explicación sencilla es bastante popular. Sin embargo, no hay evidencia que demuestre que un aumento de presión significa un aumento de fricción y, a menos que así sea, no puede haber efecto. Incluso si existiera, debe ser bastante insignificante en comparación con las derivas giroscópicas y de Coriolis.
Tanto el efecto Poisson como el efecto Magnus invertirán sus direcciones de deriva si el morro cae por debajo de la trayectoria. Cuando el morro está desviado hacia un lado, como en la guiñada de equilibrio, estos efectos producirán pequeñas alteraciones en el alcance.
Deriva de Coriolis
El efecto Coriolis provoca una desviación de Coriolis en una dirección perpendicular al eje de la Tierra; para la mayoría de las ubicaciones de la Tierra y direcciones de disparo, esta desviación incluye componentes horizontales y verticales. La desviación es hacia la derecha de la trayectoria en el hemisferio norte, hacia la izquierda en el hemisferio sur, hacia arriba para disparos hacia el este y hacia abajo para disparos hacia el oeste. La desviación de Coriolis vertical también se conoce como efecto Eötvös . La desviación de Coriolis no es un efecto aerodinámico; es una consecuencia de la rotación de la Tierra.
La magnitud del efecto Coriolis es pequeña. En el caso de las armas pequeñas , la magnitud del efecto Coriolis es generalmente insignificante (para fusiles de alta potencia, del orden de unos 10 cm (3,9 pulgadas) a 1000 m (1094 yardas)), pero en el caso de los proyectiles balísticos con tiempos de vuelo largos, como los proyectiles de fusil de alcance extremadamente largo, la artillería y los cohetes como los misiles balísticos intercontinentales , es un factor significativo para calcular la trayectoria. La magnitud de la deriva depende de la ubicación del disparo y del objetivo, del acimut del disparo, de la velocidad del proyectil y del tiempo de vuelo.
Efecto horizontal
Visto desde un marco de referencia que no gira (es decir, que no gira con la Tierra) e ignorando las fuerzas de gravedad y la resistencia del aire, un proyectil se mueve en línea recta. Cuando se observa desde un marco de referencia fijo con respecto a la Tierra, esa trayectoria recta parece curvarse lateralmente. La dirección de esta curvatura horizontal es hacia la derecha en el hemisferio norte y hacia la izquierda en el hemisferio sur, y no depende del acimut del disparo. La curvatura horizontal es máxima en los polos y disminuye hasta cero en el ecuador. [67]
Efecto vertical (Eötvös)
El efecto Eötvös cambia la atracción gravitacional percibida sobre un objeto en movimiento en función de la relación entre la dirección y la velocidad del movimiento y la dirección de la rotación de la Tierra. [68] [69]
El efecto Eötvös es mayor en el ecuador y disminuye a cero en los polos. Hace que los proyectiles que viajan hacia el este se desvíen hacia arriba y los que viajan hacia el oeste se desvíen hacia abajo. El efecto es menos pronunciado para las trayectorias en otras direcciones y es cero para las trayectorias que apuntan hacia el norte o el sur. En el caso de grandes cambios de momento, como el lanzamiento de una nave espacial a la órbita terrestre, el efecto se vuelve significativo. Contribuye a la trayectoria más rápida y con mayor eficiencia de combustible para llegar a la órbita: un lanzamiento desde el ecuador que se curva hacia un rumbo directamente hacia el este.
Factores del equipo
Aunque no se trata de fuerzas que actúen sobre las trayectorias de los proyectiles, existen algunos factores relacionados con el equipamiento que influyen en ellas. Dado que estos factores pueden provocar un comportamiento de vuelo balístico externo inexplicable, es necesario mencionarlos brevemente.
Salto lateral
El salto lateral se produce por un ligero movimiento lateral y rotatorio del cañón del arma en el momento del disparo. Tiene como consecuencia un pequeño error en la orientación. Este efecto se ignora, ya que es pequeño y varía de una ronda a otra.
Saque lateral
El desprendimiento lateral se produce por un desequilibrio de masa en los proyectiles estabilizados por giro aplicados o por desequilibrios de presión durante la fase de vuelo de transición , cuando un proyectil sale del cañón de un arma fuera de eje, lo que provoca un desequilibrio estático. Si está presente, causa dispersión. El efecto es impredecible, ya que generalmente es pequeño y varía de un proyectil a otro, de una bala a otra y/o de un cañón a otro.
Alcance máximo efectivo de armas pequeñas
El alcance práctico máximo [nota 4] de todas las armas pequeñas y, en especial, de los rifles de francotirador de alta potencia depende principalmente de la eficiencia aerodinámica o balística de los proyectiles estabilizados por giro utilizados. Los tiradores de largo alcance también deben recopilar información relevante para calcular las correcciones de elevación y de deriva para poder lograr impactos de primer disparo en objetivos puntuales. Los datos para calcular estas correcciones de control de tiro tienen una larga lista de variables que incluyen: [70]
- Coeficiente balístico o coeficiente de arrastre derivado de pruebas (Cd)/comportamiento de las balas utilizadas
- Altura de los componentes de puntería por encima del eje del cañón del rifle.
- el rango cero en el que se apuntaron los componentes de puntería y la combinación del rifle
- masa de bala
- Velocidad inicial real (la temperatura de la pólvora afecta la velocidad inicial, la ignición del cebador también depende de la temperatura)
- alcance al objetivo
- Alcance supersónico de la combinación de arma, cartucho y bala empleada
- Ángulo de inclinación en caso de disparo cuesta arriba/cuesta abajo
- Velocidad y dirección objetivo
- velocidad y dirección del viento (causa principal de la desviación horizontal de los proyectiles y generalmente la variable balística más difícil de medir y juzgar correctamente. Los efectos del viento también pueden causar desviación vertical).
- variaciones de presión atmosférica , temperatura , altitud y humedad (éstas conforman la densidad del aire ambiente )
- La gravedad de la Tierra (cambia ligeramente con la latitud y la altitud )
- Deriva giroscópica (efecto giroscópico en el plano horizontal y vertical, a menudo conocido como deriva de giro , inducido por la dirección y la velocidad de torsión del cañón)
- Deriva del efecto Coriolis ( la latitud , la dirección del fuego y los datos del hemisferio norte o sur determinan este efecto)
- Efecto Eötvös (relacionado con el efecto Coriolis, la latitud y la dirección del fuego determinan este efecto)
- Salto aerodinámico (el componente vertical de la desviación del viento cruzado causado por impulsos laterales (de viento) activados durante el vuelo libre o en la boca del cañón o muy cerca de ella, lo que provoca un desequilibrio dinámico) [57]
- Desplazamiento lateral (dispersión causada por un desequilibrio de masa en el proyectil aplicado o por el hecho de que éste sale del cañón fuera de eje, lo que genera un desequilibrio estático)
- La precisión potencial inherente y el rango de ajuste de los componentes de la mira.
- La precisión potencial inherente del rifle.
- La precisión potencial inherente de la munición.
- La precisión potencial inherente del programa informático y otros componentes de control de disparo utilizados para calcular la trayectoria.
La densidad del aire ambiente alcanza su máximo en las condiciones del nivel del mar en el Ártico. La pólvora fría también produce presiones más bajas y, por lo tanto, velocidades iniciales más bajas que la pólvora caliente. Esto significa que el alcance máximo práctico de los rifles será más corto en las condiciones del nivel del mar en el Ártico.
La capacidad de dar en el blanco a gran distancia tiene mucho que ver con la capacidad de hacer frente a factores medioambientales y meteorológicos y con un buen conocimiento de la balística exterior y de las limitaciones del equipo. Sin el apoyo (informático) y telémetros láser de alta precisión y equipos de medición meteorológica como ayuda para determinar soluciones balísticas, disparar a larga distancia a más de 1000 m (1100 yd) a distancias desconocidas se convierte en una cuestión de conjeturas incluso para los tiradores de larga distancia más expertos. [nota 5]
Lectura adicional interesante: Wikilibro de puntería
Utilizando datos balísticos
A continuación se muestra un ejemplo de una tabla balística para una bala de competición Speer de calibre .30 con cola de barco puntiaguda de 169 granos (11 g), con un BC de 0,480. Se supone que las miras están a 1,5 pulgadas (38 mm) por encima de la línea del ánima y que las miras están ajustadas para que el punto de mira y el punto de impacto coincidan a 200 yardas (183 m) y 300 yardas (274 m) respectivamente.
| Rango | 0 | 100 yardas 91 metros | 200 yardas 183 metros | 300 yardas 274 m | 400 yardas 366 metros | 500 yardas 457 metros | |
|---|---|---|---|---|---|---|---|
| Velocidad | ( pies/seg. ) | 2.700 | 2.512 | 2.331 | 2.158 | 1.992 | 1.834 |
| ( EM ) | 823 | 766 | 710 | 658 | 607 | 559 | |
| Puesta a cero para 200 yardas/184 m | |||||||
| Altura | (en) | -1,5 | 2.0 | 0 | -8,4 | -24,3 | −49,0 |
| (mm) | -38 | 51 | 0 | −213 | −617 | −1245 | |
| Puesta a cero para 300 yardas/274 m | |||||||
| Altura | (en) | -1,5 | 4.8 | 5.6 | 0 | -13,1 | −35,0 |
| (mm) | -38 | 122 | 142 | 0 | −333 | −889 | |
Esta tabla demuestra que, incluso con una bala bastante aerodinámica disparada a alta velocidad, la "caída de la bala" o cambio en el punto de impacto es significativo. Este cambio en el punto de impacto tiene dos implicaciones importantes. En primer lugar, estimar la distancia al objetivo es crítico a distancias más largas, porque la diferencia en el punto de impacto entre 400 y 500 yardas (460 m) es de 25 a 32 pulgadas (dependiendo del cero), en otras palabras, si el tirador estima que el objetivo está a 400 yardas de distancia cuando en realidad está a 500 yardas, el disparo impactará a 25 a 32 pulgadas (635 a 813 mm) por debajo de donde fue apuntado, posiblemente fallando el objetivo por completo. En segundo lugar, el rifle debe estar puesto a cero a una distancia apropiada para el alcance típico de los objetivos, porque el tirador podría tener que apuntar tan por encima del objetivo para compensar una gran caída de la bala que podría perder de vista el objetivo por completo (por ejemplo, estando fuera del campo de visión de una mira telescópica). En el ejemplo del rifle puesto a cero a 200 yd (180 m), el tirador tendría que apuntar 49 pulgadas o más de 4 pies (1,2 m) por encima del punto de impacto para un objetivo situado a 500 yd.
Véase también
- Balística interna : El comportamiento del proyectil y el propulsor antes de que salga del cañón.
- Balística de transición : El comportamiento del proyectil desde el momento en que sale de la boca del cañón hasta que se iguala la presión detrás del proyectil.
- Balística terminal : Comportamiento del proyectil al impactar con el objetivo.
- Trayectoria de un proyectil - Fórmulas matemáticas básicas de balística externa.
- Regla del tirador : Procedimientos o "reglas" que debe seguir un tirador para apuntar a objetivos situados a distancia, ya sea cuesta arriba o cuesta abajo.
- Franklin Ware Mann - Primer estudio científico de la balística externa.
- Tabla de cartuchos para pistolas y rifles
- Apuntar : calibrar la mira de un arma a distancia de modo que el punto de mira se cruce con la trayectoria a una distancia determinada, lo que permite al usuario acertar de forma constante en el objetivo apuntado.
Notas
- ^ La mayoría de los proyectiles estabilizados por giro que sufren de falta de estabilidad dinámica tienen el problema cerca de la velocidad del sonido, donde las fuerzas y momentos aerodinámicos exhiben grandes cambios. Es menos común (pero posible) que las balas muestren una falta significativa de estabilidad dinámica a velocidades supersónicas. Dado que la estabilidad dinámica está gobernada principalmente por la aerodinámica transónica, es muy difícil predecir cuándo un proyectil tendrá suficiente estabilidad dinámica (estos son los coeficientes aerodinámicos más difíciles de calcular con precisión en el régimen de velocidad más difícil de predecir (transónico)). Los coeficientes aerodinámicos que gobiernan la estabilidad dinámica: momento de cabeceo, momento Magnus y la suma del coeficiente de momento dinámico de cabeceo y ángulo de ataque (una cantidad muy difícil de predecir). Al final, hay poco que el modelado y la simulación puedan hacer para predecir con precisión el nivel de estabilidad dinámica que tendrá una bala a distancia. Si un proyectil tiene un nivel muy alto o bajo de estabilidad dinámica, el modelado puede dar la respuesta correcta. Sin embargo, si una situación está al límite (estabilidad dinámica cerca de 0 o 2) no se puede confiar en el modelado para producir la respuesta correcta. Esta es una de esas cosas que deben probarse en el campo y documentarse cuidadosamente.
- ^ Predicciones del método de predicción de coeficientes de arrastre derivados de pruebas de radar G1, G7 y Doppler (C d ) calculadas con QuickTARGET Unlimited, Lapua Edition. Predicciones de Pejsa calculadas con el software balístico basado en Pejsa de Lex Talus Corporation con el factor de constante de pendiente establecido en el valor predeterminado de 0,5. Predicciones de modelado de 6 DoF calculadas con la aplicación Lapua Ballistics 1.0 para Android.
- ^ Los ingenieros utilizan los datos de C d para crear algoritmos que utilizan tanto modelos balísticos matemáticos conocidos como datos tabulares específicos de pruebas al unísono para obtener predicciones muy cercanas al comportamiento de vuelo real.
- ^ The snipershide Archivado el 7 de noviembre de 2007 en el sitio web Wayback Machine define el alcance efectivo como: El alcance en el que una persona competente y entrenada que usa el arma de fuego tiene la capacidad de alcanzar un objetivo entre el sesenta y el ochenta por ciento de las veces. En realidad, la mayoría de las armas de fuego tienen un alcance real mucho mayor que este, pero la probabilidad de alcanzar un objetivo es baja a un alcance mayor que el efectivo. No parece haber una buena fórmula para los alcances efectivos de las diversas armas de fuego.
- ^ Un ejemplo de la precisión con la que un tirador de largo alcance debe establecer parámetros de puntería para calcular una solución balística correcta se explica con estos resultados de prueba de tiro. Un rifle Lapua Magnum .338 apuntado a 300 m disparó balas Lapua Scenar de 250 granos (16,2 g) a una velocidad inicial medida de 905 m/s. La densidad del aire ρ durante la prueba de tiro fue de 1,2588 kg/m³ . El rifle de prueba necesitó una corrección de elevación de 13,2 milésimas de pulgada (45,38 MOA ) desde un rango cero de 300 m a 61 grados de latitud ( la gravedad cambia ligeramente con la latitud) para alcanzar un objetivo del tamaño de un torso humano en el centro muerto a 1400 m. El gráfico de la curva balística mostró que entre 1392 m y 1408 m las balas habrían alcanzado un objetivo de 60 cm (2 pies) de altura. Esto significa que si se cometiera un error de medición de tan solo el 0,6%, un objetivo de 60 cm de altura a 1400 m se habría perdido por completo. Cuando el mismo objetivo se colocaba a una distancia menos desafiante de 1000 m, se podía alcanzar entre 987 m y 1013 m, lo que significa que un error de medición del 1,3% sería aceptable para poder alcanzar un objetivo de 2 MOA de altura con un proyectil de francotirador Lapua Magnum .338. Esto hace evidente que, a medida que aumenta la distancia, los errores de medición y de juicio aparentemente menores se convierten en un problema importante.
Referencias
- ^ Diseño para el control de las características de vuelo de los proyectiles, AMCP 706–242, Comando de Material del Ejército de los EE. UU., 1966
- ^ Ejército (febrero de 1965), Balística interior de armas (PDF) , Manual de diseño de ingeniería: serie balística, Comando de material del ejército de los Estados Unidos, págs. 1-2, AMCP 706-150, archivado desde el original (PDF) el 8 de enero de 2016
- ^ "Alcance máximo a quemarropa y Battlesight Zero". 30 de abril de 2010. Consultado el 24 de diciembre de 2022 .
- ^ "Un Battlesight Zero mejorado para la carabina M4 y el rifle M16A2" . Consultado el 11 de septiembre de 2007 .
- ^ "TM 9-1005-319-10 (2010) - Manual del operador para rifle, 5,56 mm, M16A2/M16A3/M4 (Battlesight Zero páginas 48-55)" (PDF) . Consultado el 3 de junio de 2014 .
- ^ "Usando un cero de 400 metros con 5.45×39" . Consultado el 16 de noviembre de 2014 .
- ^ "Predicción del rendimiento, la estabilidad y el movimiento en vuelo libre de proyectiles mediante dinámica de fluidos computacional, Weinacht, Laboratorio de investigación del ejército de EE. UU., 2003" (PDF) . Archivado desde el original (PDF) el 21 de enero de 2021. Consultado el 2 de junio de 2022 .
- ^ "¡Los coeficientes balísticos no existen!" . Consultado el 12 de enero de 2017 .
- ^ "Weite Schüsse - drei (alemán)". Archivado desde el original el 24 de mayo de 2008 . Consultado el 24 de diciembre de 2022 .
- ^ "balística exterior". Archivado desde el original el 8 de agosto de 2003. Consultado el 12 de enero de 2017 .
- ^ "Balas de la clase LM, balas con un BC muy alto para largas distancias con viento". Archivado desde el original el 19 de febrero de 2008. Consultado el 24 de diciembre de 2022 .
- ^ Litz, Bryan (8 de marzo de 2021) [Publicado originalmente el 17 de junio de 2009, ampliado posteriormente]. "Un coeficiente balístico mejor". Archivado desde el original el 2 de agosto de 2009.
- ^ "Folleto de producto Lapua Magnum .338 de Lapua" (PDF) . Consultado el 24 de diciembre de 2022 .[ enlace muerto permanente ]
- ^ "Folleto de Scenar HPBT de 300 grs de Lapua" (PDF) . Consultado el 24 de diciembre de 2022 .[ enlace muerto permanente ]
- ^ "Coeficientes balísticos: explicación" (PDF) . Archivado desde el original (PDF) el 29 de octubre de 2013 . Consultado el 12 de enero de 2017 .
- ^ "Modelado matemático de trayectorias de proyectiles bajo la influencia de efectos ambientales, Ryan F. Hooke,∗Universidad de Nueva Gales del Sur, Canberra, en la Academia de la Fuerza de Defensa Australiana, 2612, Australia". Archivado desde el original el 4 de febrero de 2018. Consultado el 2 de febrero de 2018 .
- ^ "Factores de forma: una herramienta de análisis útil - Blog de Berger Bullets". 16 de mayo de 2011. Consultado el 12 de enero de 2017 .
- ^ Acerca de Art Pejsa Archivado el 29 de agosto de 2008 en Wayback Machine.
- ^ Pejsa, Arthur. «Pejsa Rifle Ballistics: software y libros de Art Pejsa sobre balística de rifles». Pejsa Ballistics . Pejsa Ballistics. Archivado desde el original el 8 de febrero de 2012. Consultado el 31 de julio de 2018 .
- ^ Arthur J Pejsa (2002). Manual de Pejsa sobre balística de precisión nueva . Kenwood Publishing. pág. 3.
- ^ por Arthur J Pejsa (2008). New Exact Small Arms Ballistics [Nueva balística exacta para armas pequeñas ]. Kenwood Publishing. págs. 65–76.
- ^ Arthur J Pejsa (2008). Balística de armas pequeñas New Exact . Kenwood Publishing. pág. 63.
- ^ Arthur J Pejsa (2002). Manual de Pejsa sobre balística de precisión nueva . Kenwood Publishing. pág. 34.
- ^ Arthur J Pejsa (2002). Manual de Pejsa sobre balística de precisión nueva . Kenwood Publishing. pág. 4.
- ^ Arthur J Pejsa (2008). Balística de armas pequeñas New Exact . Kenwood Publishing. págs. 131–134.
- ^ Meijer, Robert. «Pejsa y funciones habituales de arrastre» . Consultado el 12 de enero de 2017 .
- ^ Arthur J Pejsa (2008). Balística de armas pequeñas New Exact . Kenwood Publishing. págs. 33–35.
- ^ "Opciones de prueba y técnicas de análisis: coeficientes aerodinámicos: ¿qué es importante y cómo puedo medirlos? Jeff Siewert, ingeniero de sistemas, Arrow Tech Associates, Inc., 2012, NDIA Joint Armaments" (PDF) . Archivado desde el original (PDF) el 13 de diciembre de 2016. Consultado el 15 de octubre de 2016 .
- ^ SPIN-73 Una versión actualizada del programa informático Spinner, White, 1973
- ^ Manual de diseño aerodinámico para armas tácticas, NSWC 1981
- ^ Modelado de sólidos mejorado para el diseño de proyectiles axisimétricos, 1988
- ^ "Modelo de simulación digital de seis grados de libertad para cohetes no guiados estabilizados por aletas" (PDF) . Archivado desde el original (PDF) el 2017-02-21 . Consultado el 24 de diciembre de 2022 .
- ^ "Aplicación Lapua Ballistics - Recursos - Nammo Lapua". Archivado desde el original el 20 de diciembre de 2016 . Consultado el 12 de enero de 2017 .
- ^ "KIT DE HERRAMIENTAS DE MESA BALÍSTICA DE PRÓXIMA GENERACIÓN BASADO EN NABK, Sevsay Aytar Ortac, Umut Durak, Umit Kutluay, Koray Kucuk, Mayor Can Candan, 23º SIMPOSIO INTERNACIONAL DE BALÍSTICA, TARRAGONA, ESPAÑA, 16-20 DE ABRIL DE 2007" . Consultado el 24 de diciembre de 2022 .
- ^ "Modelo de trayectoria BALCO 6/7-DoF, Pierre Wey, Daniel Corriveau, Thomas A. Saitz, Wim de Ruijter, Peter Strömbäck, 29º Simposio internacional sobre balística, Edimburgo, Escocia, 9 al 13 de mayo de 2016" . Consultado el 24 de diciembre de 2022 .
- ^ Corriveau, D. (2017). "Validación del núcleo balístico de armamentos de la OTAN para su uso en sistemas de control de fuego de armas pequeñas". Tecnología de defensa . 13 (3): 188–199. doi : 10.1016/j.dt.2017.04.006 .
- ^ "Discusión técnica sobre las balas ELD-X™ (Extremely Low Drag – eXpanding) y ELD™ Match (Extremely Low Drag Match) con punta Heat Shield™, Dave Emary, octubre de 2015" (PDF) . Archivado desde el original (PDF) el 2015-11-06 . Consultado el 2015-11-01 .
- ^ Chuck Hawks. "El calibre 8x50R Lebel (Lebel de 8 mm)".
- ^ Richardson contra Estados Unidos, 72 Ct. Cl. 51 (1930)
- ^ MC DRAG - Un programa informático para estimar los coeficientes de arrastre de los proyectiles, McCoy, Laboratorio de investigación balística del ejército de EE. UU., 1981
- ^ «Nueva serie de vídeos de Applied Ballistics « Daily Bulletin». Archivado desde el original el 21 de octubre de 2016 . Consultado el 12 de enero de 2017 .
- ^ "El efecto de la geometría de cola de barco en el ciclo límite de guiñada de proyectiles de pequeño calibre por Bradley E. Howell Data Matrix Solutions, Aberdeen Proving Ground, MD 21005-5066 y Sidra I. Silton y Paul Weinacht Weapons and Materials Research Directorate, ARL, Aberdeen Proving Ground, MD 21005-5066 27th AIAA Applied Aerodynamics Conference 22 - 25 June 2009, San Antonio, Texas" (PDF) . Archivado desde el original (PDF) el 2016-04-06 . Consultado el 2015-01-11 .
- ^ "EFECTO DE LAS RANURAS DEL RANURADO EN EL RENDIMIENTO DE MUNICIONES DE PEQUEÑO CALIBRE Sidra I. Silton y Paul Weinacht Laboratorio de Investigación del Ejército de EE. UU. Campo de pruebas de Aberdeen, MD 21005-5066". Archivado desde el original el 11 de enero de 2015. Consultado el 24 de diciembre de 2022 .
- ^ "Sandia National Laboratories: Comunicados de prensa: El prototipo de bala autoguiada de Sandia puede alcanzar un objetivo a una milla de distancia". Archivado desde el original el 5 de febrero de 2012. Consultado el 12 de enero de 2017 .
- ^ "Proyectil calibre .50 guiado: la bala orientable de DARPA" . Consultado el 27 de septiembre de 2020 .
- ^ Courtney, Elya, Collin Morris y Michael Courtney. "Medidas precisas de coeficientes de resistencia aerodinámica en vuelo libre con radar Doppler amateur". Biblioteca de la Universidad de Cornell (2016). arXiv :1608.06500
- ^ "Datos del coeficiente de arrastre de las balas Lapua para QuickTARGET Unlimited" (PDF) . Archivado desde el original (PDF) el 2010-12-29 . Consultado el 24 de diciembre de 2022 .
- ^ "Datos del CD de balas de Lapua (archivo zip)" . Consultado el 24 de diciembre de 2022 .[ enlace muerto permanente ]
- ^ "Uso del radar Doppler para generar soluciones de trayectorias" (PDF) . Archivado desde el original (PDF) el 23 de septiembre de 2015 . Consultado el 22 de julio de 2015 .
- ^ "Descripción general de la calculadora balística Hornady® 4DOF". Archivado desde el original el 23 de agosto de 2016. Consultado el 12 de enero de 2017 .
- ^ "Calculadora balística de 4 grados de libertad" . Consultado el 12 de enero de 2017 .
- ^ "Variabilidad de la resistencia y el uso del "factor de forma axial" en la calculadora de trayectorias Hornady 4DOF™" (PDF) . Archivado desde el original (PDF) el 19 de octubre de 2016 . Consultado el 14 de octubre de 2016 .
- ^ "Documento técnico de la calculadora balística Hornady® 4DOF™ (cuatro grados de libertad)" (PDF) . Archivado desde el original (PDF) el 2016-10-19 . Consultado el 2016-10-14 .
- ^ "QuickTARGET Unlimited, Lapua Edition". Archivado desde el original el 1 de julio de 2012. Consultado el 24 de diciembre de 2022 .
- ^ "Software balístico exterior gratuito Lapua Ballistics para teléfonos móviles". Archivado desde el original el 1 de julio de 2012. Consultado el 24 de diciembre de 2022 .
- ^ "EFECTO DE LAS RANURAS DEL RANURADO EN EL RENDIMIENTO DE MUNICIONES DE PEQUEÑO CALIBRE Sidra I. Silton* y Paul Weinacht Laboratorio de Investigación del Ejército de EE. UU. Campo de pruebas de Aberdeen, MD 21005-5066". Archivado desde el original el 6 de octubre de 2012. Consultado el 24 de diciembre de 2022 .
- ^ ab Los efectos del salto aerodinámico causado por una secuencia uniforme de impulsos laterales - Gene R. Cooper, julio de 2004
- ^ "Entender los tiros cuesta arriba y cuesta abajo en tiros de largo alcance: una introducción". backcountrymaven.com. 16 de mayo de 2013. Archivado desde el original el 25 de noviembre de 2014. Consultado el 28 de marzo de 2017 .
- ^ William T. McDonald (junio de 2003). "FUEGO INCLINADO". Exterior Ballistics.com. Archivado desde el original el 25 de noviembre de 2014. Consultado el 12 de enero de 2017 .
- ^ Beckstrand, Tom (6 de febrero de 2020). "Efectos de la lluvia en la trayectoria de las balas". Armas y municiones . Consultado el 24 de diciembre de 2022 .
- ^ Nenstiel El ángulo de reposo de una bala M80 (7,62 x 51 Nato) disparada a 32°
- ^ Nennstiel, Ruprecht. "más largo" . Consultado el 12 de enero de 2017 .
- ^ "Artículos - Applied Ballistics LLC". Archivado desde el original el 7 de enero de 2016 . Consultado el 12 de enero de 2017 .
- ^ Nenstiel El efecto Magnus
- ^ Nenstiel La fuerza de Magnus
- ^ Nenstiel El momento Magnus
- ^ "Deriva giroscópica y aceleración de Coreolis por Bryan Litz". Archivado desde el original el 14 de noviembre de 2007. Consultado el 24 de junio de 2008 .
- ^ "El efecto Eötvös". www.cleonis.nl . Consultado el 24 de diciembre de 2022 .
- ^ Lowrie, William (1997). Fundamentos de geofísica (edición ilustrada). Cambridge University Press. pág. 45. ISBN 0-521-46728-4.Extracto de la página 45
- ^ El Laboratorio de Investigación del Ejército de los Estados Unidos realizó un estudio en 1999 sobre los límites prácticos de varios sistemas de armas de francotirador y diferentes métodos de control de fuego. Análisis del presupuesto de error de control de fuego de armas de francotirador - Raymond Von Wahlde, Dennis Metz, agosto de 1999
Enlaces externos
Balística externa general
- Tan, A.; Frick, CH y Castillo, O. (1987). "La trayectoria de la pelota al aire: un enfoque antiguo revisado". American Journal of Physics . 55 (1): 37. Bibcode :1987AmJPh..55...37T. doi :10.1119/1.14968.(Cálculo simplificado del movimiento de un proyectil bajo una fuerza de arrastre proporcional al cuadrado de la velocidad)
- "El tiro perfecto de baloncesto" (PDF) . (PDF) . Archivado desde el original (PDF) el 5 de marzo de 2006 . Consultado el 26 de septiembre de 2005 .- balística del baloncesto.
Balística externa de armas pequeñas
- Software para calcular la balística de balones
- ¿Cómo vuelan las balas? por Ruprecht Nennstiel, Wiesbaden, Alemania
- Artículos de Exterior Ballistics.com Archivados el 6 de marzo de 2013 en Wayback Machine
- Curso breve sobre balística externa
- Artículos sobre tiro a larga distancia de Bryan Litz
- Análisis probabilístico de la zona de empleo de armas (ZEE): una descripción conceptual por Bryan Litz Archivado el 23 de septiembre de 2015 en Wayback Machine
- Weite Schüsse - parte 4, Explicación básica del modelo Pejsa por Lutz Möller (en alemán)
- Motor de software matemático balístico de Patagonia Ballistics
- Balística de armas pequeñas de JBM con calculadoras balísticas en línea
- Calculadora balística en línea de masa puntual de Bison Ballistics Archivado el 15 de mayo de 2011 en Wayback Machine
- Experimentos en túnel de viento virtual para caracterización aerodinámica de municiones de pequeño calibre - Paul Weinacht Laboratorio de investigación del ejército de EE. UU. Campo de pruebas de Aberdeen, Maryland
Balística externa de artillería
- Control de fuego de artillería británica: balística y datos
- Artillería de campaña, volumen 6, balística y municiones
- La producción de tablas de tiro para artillería de cañón, informe BRL n.º 1371 de Elizabeth R. Dickinson, Laboratorios de investigación balística del Comando de Material del Ejército de los EE. UU., noviembre de 1967
- Mesa de trabajo balística de próxima generación basada en el núcleo balístico de armamento de la OTAN (NABK), 23.º Simposio internacional sobre balística, Tarragona (España), 16-20 de abril de 2007
- Calculadora de trayectoria en C++ que puede deducir la función de arrastre a partir de tablas de disparo
Software gratuito de balística externa para armas pequeñas
- Aplicación balística GRATUITA Hawke X-ACT Pro. iOS, Android, OSX y Windows.
- ChairGun Pro, balística gratuita para pistolas de perdigones y de fuego anular.
- Ballistic_XLR. (Hoja de cálculo de MS Excel)] - Una mejora y modificación sustancial de la hoja de cálculo de Pejsa (abajo).
- GNU Exterior Ballistics Computer (GEBC): una computadora balística 3DOF de código abierto para Windows, Linux y Mac. Admite los modelos de resistencia G1, G2, G5, G6, G7 y G8. Creada y mantenida por Derek Yates.
- La sección de balística de 6mmbr.com contiene enlaces a/aloja 4 programas informáticos de balística externos gratuitos.
- 2DOF y 3DOF RL McCoy - Balística exterior de Gavre (archivo zip) - Admite los modelos de arrastre G1, G2, G5, G6, G7, G8, GS, GL, GI, GB y RA4
- PointBlank Ballistics (archivo zip): modelo de arrastre Siacci/Mayevski G1.
- Remington Shoot! Calculadora balística para munición de fábrica Remington (basada en el software Shoot! de Pinsoft). - Modelo de arrastre Siacci/Mayevski G1.
- Calculadoras balísticas de armas pequeñas de JBM Calculadoras de trayectoria en línea: admite los modelos de arrastre G1, G2, G5, G6, G7 (para algunos proyectiles, coeficientes balísticos G7 medidos experimentalmente), G8, GI, GL y para algunos proyectiles, modelos de arrastre derivados de pruebas de radar Doppler (C d ). [1]
- Balística Pejsa (hoja de cálculo MS Excel) - Modelo Pejsa.
- Sharpshooter Friend (software para PDA Palm) - Modelo Pejsa.
- Quick Target Unlimited, Lapua Edition: una versión del software balístico QuickTARGET Unlimited (requiere registro gratuito para descargarlo). Admite los modelos de arrastre derivados de pruebas de radar Doppler (Cd) G1, G2, G5, G6, G7, G8, GL, GS Spherical 9/16"SAAMI, GS Spherical Don Miller, RA4, Soviet 1943, British 1909 Hatches Notebook y algunos proyectiles Lapua.
- Software balístico exterior Lapua Ballistics para teléfonos móviles Java o Android. Basado en modelos de resistencia al avance (Cd) derivados de pruebas de radar Doppler para proyectiles y cartuchos Lapua.
- Aplicación Lapua Ballistics, modelo 6 DoF limitado a balas Lapua para Android e iOS.
- BfX - Balística para Excel Conjunto de funciones de complementos de MS Excel: compatible con los modelos de arrastre G1, G2, G5, G6, G7, G8, RA4 y Pejsa, así como uno para balines de rifle de aire comprimido. Puede manejar modelos proporcionados por el usuario, por ejemplo, los proyectiles Lapua derivados de la prueba de radar Doppler (Cd).
- "GunSim" es un programa de simulación balística gratuito basado en navegador para Windows y Mac.
- BallisticSimulator "Ballistic Simulator" programa simulador balístico gratuito para Windows.
- 5H0T Calculadora balística gratuita en línea basada en web, con capacidad de exportación de datos y gráficos.
- Calculadora balística en línea gratuita de SAKO. Calculadora también disponible como aplicación para Android (quizás también para iOS, no lo sé) con el nombre "SAKO Ballistics " .
- py-ballisticcalc Biblioteca LGPL de Python para cálculos balísticos de masa puntual.
- ^ "Biblioteca de balas JBM". Archivado desde el original el 3 de mayo de 2010. Consultado el 24 de diciembre de 2022 .