Solitario de clavijas
Juego de mesa para un jugador
La princesa de Soubise jugando al solitario, 1697

Peg Solitaire , Solo Noble , Solo Goli , Marble Solitaire o simplemente Solitaire es un juego de mesa para un jugador que implica el movimiento de fichas en un tablero con agujeros. Algunos juegos utilizan canicas en un tablero con hendiduras. El juego se conoce como solitario en Gran Bretaña y como peg solitaire en los EE. UU., donde "solitario" es ahora el nombre común para la paciencia .

La primera evidencia del juego se remonta a la corte de Luis XIV y la fecha específica de 1697, con un grabado realizado diez años después por Claude Auguste Berey de Anne de Rohan-Chabot , princesa de Soubise, con el rompecabezas a su lado. La edición de agosto de 1697 de la revista literaria francesa Mercure galant contiene una descripción del tablero, las reglas y problemas de muestra. Esta es la primera referencia conocida al juego impresa.

El juego estándar llena todo el tablero con fichas, excepto el agujero central. El objetivo es, realizando movimientos válidos, vaciar todo el tablero, excepto una ficha solitaria en el agujero central.

Junta

Hay dos tableros tradicionales ('.' como clavija inicial, 'o' como agujero inicial):

Ingléseuropeo
 · · · · · · · · · · · · · · · · o · · · · · · · · · · · · · · · ·
 · · · · · · · · · · · · · · · · · · o · · · · · · · · · · · · · · · · · ·

Jugar

Jugando al solitario Peg
Hombre jugando al solitario con fichas triangulares

Un movimiento válido es hacer saltar una clavija ortogonalmente sobre una clavija adyacente hasta un agujero situado dos posiciones más allá y luego retirar la clavija saltada.

En los diagramas que siguen, ·indica una clavija en un agujero, *en negrita indica la clavija que se va a mover y en rojo oindica un agujero vacío. El azul ¤es el agujero del que se movió la clavija actual; el rojo *es la posición final de esa clavija; el rojo oes el agujero de la clavija que se saltó y se eliminó.

Por lo tanto, los movimientos válidos en cada una de las cuatro direcciones ortogonales son:

* · o → ¤  o  *  Saltar a la derecha
o · * → *  o  ¤  Saltar a la izquierda
*  ¤
· → o  Saltar hacia abajo
o *
o *
· → o  Saltar arriba *  ¤

En un tablero inglés, los tres primeros movimientos podrían ser:

 · · · · · · · · · · · · · · * · · ¤ · · o · · * ·· · · · · · · · · · o · · · · ¤  o  * · · · · oo o · · ·· · · o · · · · · · * · · · · · · · · · · · · · ¤ · · ·· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Estrategia

Hay muchas soluciones diferentes al problema estándar, y una notación utilizada para describirlas asigna letras a los agujeros (aunque también se pueden usar números):

 Inglés europeo abccabc desafiar a defzghijklmghijklmnopx PON nopx PONMLKJIHGMLKJIHG FEDERACIÓN FEDERAL CBAACBA

Esta notación de imagen especular se utiliza, entre otras razones, porque en el tablero europeo, una serie de juegos alternativos consiste en empezar con un agujero en una posición determinada y terminar con una sola clavija en su posición reflejada. En el tablero inglés, los juegos alternativos equivalentes consisten en empezar con un agujero y terminar con una clavija en la misma posición.

No hay solución para el tablero europeo con el agujero inicial situado en el centro, si sólo se permiten movimientos ortogonales. Esto se ve fácilmente de la siguiente manera, mediante un argumento de Hans Zantema . Divida las posiciones del tablero en posiciones A, B y C de la siguiente manera:

 abecedario ABCABABCABCABCABCABC BCABC abecedario

Inicialmente, con solo la posición central libre, el número de posiciones A cubiertas es 12, el número de posiciones B cubiertas es 12 y también el número de posiciones C cubiertas es 12. Después de cada movimiento, el número de posiciones A cubiertas aumenta o disminuye en uno, y lo mismo ocurre con el número de posiciones B cubiertas y el número de posiciones C cubiertas. Por lo tanto, después de un número par de movimientos, todos estos tres números son pares, y después de un número impar de movimientos, todos estos tres números son impares. Por lo tanto, no se puede llegar a una posición final con una sola clavija, ya que eso requeriría que uno de estos números sea uno (la posición de la clavija, uno es impar), mientras que los otros dos números son cero, es decir, pares.

Sin embargo, existen otras configuraciones en las que un único orificio inicial puede reducirse a una única clavija.

Una táctica que se puede utilizar es dividir el tablero en paquetes de tres y purgarlos (eliminarlos) por completo utilizando una clavija adicional, el catalizador, que salta y luego vuelve a saltar . En el ejemplo siguiente, el * es el catalizador:

* · o ¤  o  * o * · *  o  ¤ · → · → o → o · · ¤ o

Esta técnica se puede utilizar con una línea de 3, un bloque de 2,3 y una L de 6 clavijas con una base de longitud 3 y un montante de longitud 4.

Otros juegos alternativos incluyen comenzar con dos agujeros vacíos y terminar con dos clavijas en esos agujeros. También comenzar con un agujero aquí y terminar con una clavija allí . En un tablero inglés, el agujero puede estar en cualquier lugar y la clavija final solo puede terminar donde lo permitan los múltiplos de tres. Por lo tanto, un agujero en a solo puede dejar una única clavija en a , p , O o C .

Estudios sobre el solitario de clavijas

Se conoce un análisis exhaustivo del juego. [1] Este análisis introdujo una noción llamada función pagoda que es una herramienta poderosa para mostrar la inviabilidad de un problema de solitario de clavijas generalizado dado.

Una solución para encontrar una función pagoda, que demuestra la inviabilidad de un problema dado, se formula como un problema de programación lineal y se puede resolver en tiempo polinomial. [2]

Un artículo de 1990 abordó los problemas Hi-Q generalizados que son equivalentes a los problemas de solitario de clavijas y mostró su NP-completitud . [3]

Un artículo de 1996 formuló un problema de solitario de clavijas como un problema de optimización combinatoria y analizó las propiedades de la región factible denominada "cono solitario". [4]

En 1999, el solitario de clavijas se resolvió completamente en un ordenador mediante una búsqueda exhaustiva entre todas las variantes posibles. Se logró haciendo uso de las simetrías, el almacenamiento eficiente de las constelaciones del tablero y el hashing. [5]

En 2001 se desarrolló un método eficiente para resolver problemas de solitario de clavijas. [2]

Un estudio inédito de 1989 sobre una versión generalizada del juego en el tablero inglés mostró que cada posible problema en el juego generalizado tiene 2 9 posibles soluciones distintas, excluyendo las simetrías, ya que el tablero inglés contiene 9 subcuadrados distintos de 3 × 3. Una consecuencia de este análisis es poner un límite inferior al tamaño de los posibles problemas de "posición invertida", en los que las celdas ocupadas inicialmente se dejan vacías y viceversa. Cualquier solución a un problema de este tipo debe contener un mínimo de 11 movimientos, independientemente de los detalles exactos del problema.

Se puede demostrar usando álgebra abstracta que sólo hay cinco posiciones fijas del tablero en las que el juego puede terminar exitosamente con una clavija. [6]

Soluciones al juego de inglés

Guía de soluciones interactivas para el solitario Peg inglés.

La solución más corta del juego inglés estándar implica 18 movimientos, contando los saltos múltiples como movimientos individuales:

Esta solución fue encontrada en 1912 por Ernest Bergholt y John Beasley demostró ser la más corta posible en 1964. [7]

Esta solución también se puede ver en una página que también presenta la notación Wolstenholme, que está diseñada para facilitar la memorización de la solución.

Otras soluciones incluyen la siguiente lista. En ellas, la notación utilizada es

  • Lista de hoyos de inicio
  • Colon
  • Lista de clavijas de destino final
  • Signo igual
  • Clavija de origen y agujero de destino (las clavijas saltadas se dejan como ejercicio para el lector)
  • , o / ( se utiliza una barra para separar 'fragmentos' como, por ejemplo, una purga de seis )
x:x=ex,lj,ck,Pf,DP,GI,JH,mG,GI,ik,gi,LJ,JH,Hl,lj,jh,CK,pF,AC,CK,Mg,gi,ac, ck,kI,dp,pF,FD,DP,Pp,ox x:x=ex,lj,xe/hj,Ki,jh/ai,ca,fd,hj,ai,jh/MK,gM,hL,Fp,MK,pF/CK,DF,AC,JL,CK, LJ/PD, GI, mG, JH, GI, DP/Ox j:j=lj,Ik,jl/hj,Ki,jh/mk,Gm,Hl,fP,mk,Pf/ai,ca,fd,hj,ai,jh/MK,gM,hL,Fp,MK,pF/CK,DF,AC,JL,CK,LJ/Jj i:i=ki,Jj,ik/lj,Ik,jl/AI,FD,CA,HJ,AI,JH/mk,Hl,Gm,fP,mk,Pf/ai,ca,fd,hj,ai, jh/gi,Mg,Lh,pd,gi,dp/Ki e:e=xe/lj,Ik,jl/ck,ac,df,lj,ck,jl/GI,lH,mG,DP,GI,PD/AI,FD,CA,JH,AI,HJ/pF, MK,gM,JL,MK,Fp/hj,ox,xe d:d=fd,xe,df/lj,ck,ac,Pf,ck,jl/DP,KI,PD/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK, JL/MK,gM,hL,pF,MK,Fp/pd b:b=jb,lj/ck,ac,Pf,ck/DP,GI,mG,JH,GI,PD/LJ,CK,JL/MK,gM,hL,pF,MK,Fp/xo,dp, buey/xe/AI/BJ,JH,Hl,lj,jb b:x=jb,lj/ck,ac,Pf,ck/DP,GI,mG,JH,GI,PD/LJ,CK,JL/MK,gM,hL,pF,MK,Fp/xo,dp, buey/xe/AI/BJ,JH,Hl,lj,ex a:a=ca,jb,ac/lj,ck,jl/Ik,pP,KI,lj,Ik,jl/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK, JL/dp,gi,pd,Mg,Lh,gi/ia a:p=ca,jb,ac/lj,ck,jl/Ik,pP,KI,lj,Ik,jl/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK, JL/dp,gi,pd,Mg,Lh,gi/dp
Una solución fácil de recordar es limpiar primero los bordes concentrándose en los agujeros marcados con un círculo blanco: en la figura 1, las clavijas están etiquetadas en el orden en que se quitan.

Ataque de fuerza bruta en el solitario de clavijas inglés estándar

El único lugar en el que es posible terminar con una clavija solitaria es en el centro o en la mitad de uno de los bordes; en el último salto, siempre habrá la opción de elegir si terminar en el centro o en el borde.

A continuación se muestra una tabla con el número ( posibilidades de posiciones del tablero ) de posibles posiciones del tablero después de n saltos , y la posibilidad de que la misma ficha se mueva para realizar un salto adicional ( N o más saltos ). Es interesante notar que la forma más corta de perder el juego es en seis movimientos, y la solución (además de sus rotaciones y reflexiones) es única. Un ejemplo de esto es el siguiente: 4 → 16; 23 → 9; 14 → 16; 17 → 15; 19 → 17; 31 → 23. (En esta notación, las fichas están numeradas de izquierda a derecha, comenzando con 0 y moviéndose hacia abajo en cada fila y hacia el extremo izquierdo una vez que se marca cada fila).

NOTA: Si una posición del tablero se puede rotar y/o voltear hacia otra posición del tablero, las posiciones del tablero se cuentan como idénticas.

Dado que solo puede haber 31 saltos, las computadoras modernas pueden examinar fácilmente todas las posiciones del juego en un tiempo razonable. [8]

La secuencia anterior "PBP" se ha introducido como A112737 en OEIS . Tenga en cuenta que el número total de posiciones de placa alcanzables (suma de la secuencia) es 23.475.688, mientras que el número total de posiciones de placa posibles es 8.589.934.590 (33 bit-1) (2^33), por lo que solo se puede alcanzar alrededor del 2,2 % de todas las posiciones de placa posibles comenzando con el centro vacante.

También es posible generar todas las posiciones del tablero. Los resultados que se muestran a continuación se obtuvieron utilizando el conjunto de herramientas mCRL2 (consulte el ejemplo peg_solitaire en la distribución).

En los resultados a continuación, ha generado todas las posiciones del tablero que realmente alcanzó comenzando con el centro vacante y terminando en el agujero central.

Soluciones al juego europeo

Hay 3 posiciones iniciales no congruentes que tienen soluciones. [9] Estas son:

1)

 0 1 2 3 4 5 6 0 o · · 1 · · · · · 2 · · · · · · · 3 · · · · · · · 4 · · · · · · · 5 · · · · · 6 · · ·

Posible solución: [2:2-0:2, 2:0-2:2, 1:4-1:2, 3:4-1:4, 3:2-3:4, 2:3-2:1, 5:3-3:3, 3:0-3:2, 5:1-3:1, 4:5-4:3, 5:5-5:3, 0:4-2:4, 2:1-4:1, 2:4-4:4, 5:2-5:4, 3:6-3:4, 1:1-1:3, 2:6-2:4, 0:3-2:3, 3:2-5:2, 3:4-3:2, 6:2-4:2, 3:2-5:2, 4:0-4:2, 4:3-4:1, 6:4-6:2, 6:2-4:2, 4:1-4:3, 4:3-4:5, 4:6-4:4, 5:4-3:4, 3:4-1:4, 1:5-1:3, 2:3-0:3, 0:2-0:4]

2)

 0 1 2 3 4 5 6 0 · · · 1 · · o · · 2 · · · · · · · 3 · · · · · · · 4 · · · · · · · 5 · · · · · 6 · · ·

Posible solución: [1:1-1:3, 3:2-1:2, 3:4-3:2, 1:4-3:4, 5:3-3:3, 4:1-4:3, 2:1-4:1, 2:6-2:4, 4:4-4:2, 3:4-1:4, 3:2-3:4, 5:1-3:1, 4:6-2:6, 3:0-3:2, 4:5-2:5, 0:2-2:2, 2:6-2:4, 6:4-4:4, 3:4-5:4, 2:3-2:1, 2:0-2:2, 1:4-3:4, 5:5-5:3, 6:3-4:3, 4:3-4:1, 6:2-4:2, 3:2-5:2, 4:0-4:2, 5:2-3:2, 3:2-1:2, 1:2-1:4, 0:4-2:4, 3:4-1:4, 1:5-1:3, 0:3-2:3]

y 3)

 0 1 2 3 4 5 6 0 · · · 1 · · · · · 2 · · · o · · · 3 · · · · · · · 4 · · · · · · · 5 · · · · · 6 · · ·

Posible solución: [2:1-2:3, 0:2-2:2, 4:1-2:1, 4:3-4:1, 2:3-4:3, 1:4-1:2, 2:1-2:3, 0:4-0:2, 4:4-4:2, 3:4-1:4, 6:3-4:3, 1:1-1:3, 4:6-4:4, 5:1-3:1, 2:6-2:4, 1:4-1:2, 0:2-2:2, 3:6-3:4, 4:3-4:1, 6:2-4:2, 2:3-2:1, 4:1-4:3, 5:5-5:3, 2:0-2:2, 2:2-4:2, 3:4-5:4, 4:3-4:1, 3:0-3:2, 6:4-4:4, 4:0-4:2, 3:2-5:2, 5:2-5:4, 5:4-3:4, 3:4-1:4, 1:5-1:3]

Variantes de la placa

El solitario de clavijas se ha jugado en tableros de otros tamaños, aunque los dos que se mencionan arriba son los más populares. También se ha jugado en un tablero triangular, con saltos permitidos en las tres direcciones. Siempre que la variante tenga la "paridad" adecuada y sea lo suficientemente grande, probablemente se pueda resolver.

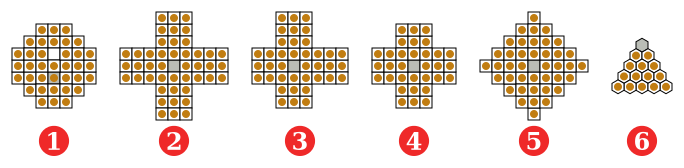
Formas del tablero del juego de solitario Peg:
(1) estilo francés (europeo), 37 agujeros, siglo XVII;
(2) JC Wiegleb, 1779, Alemania, 45 agujeros;
(3) asimétrico 3-3-2-2 como lo describió George Bell, siglo XX; [10]
(4) estilo inglés (estándar), 33 agujeros;
(5) diamante, 41 agujeros;
(6) triangular, 15 agujeros.
Gris = el agujero para el sobreviviente.

Una variante triangular común tiene cinco clavijas en cada lado. Una solución en la que la clavija final llega al agujero vacío inicial no es posible para un agujero en una de las tres posiciones centrales. Una configuración de agujero vacío en la esquina se puede resolver en diez movimientos, y una configuración de agujero vacío en el medio del lado en nueve (Bell 2008):

Videojuego

El 26 de junio de 1992 se lanzó un videojuego basado en el solitario de clavijas para Game Boy. Titulado simplemente Solitaire , el juego fue desarrollado por Hect. En Norteamérica, DTMC lanzó el juego como Lazlos' Leap .

El juego para PC Shivers , un juego de rompecabezas de tipo point and click con temática de terror , incluye muchos rompecabezas y juegos para que el jugador los complete. El rompecabezas denominado "Damas chinas" es en realidad un solitario de fichas.

Cracker Barrel ofrece el juego en todas las mesas de sus sucursales. El tablero que se muestra es triangular con 15 hoyos en total.

En Cowboy Bebop: La Película , el antagonista principal, Vincent Volaju, pasa la mayor parte de su tiempo libre jugando al solitario. El vector para su ataque bioterrorista planeado, un tipo de nanobot , está almacenado en canicas de solitario.

Referencias

  1. ^ Berlekamp, ​​ER ; Conway, JH ; Guy, RK (2001) [1981], Maneras ganadoras para sus jugadas matemáticas (2.ª ed.), AK Peters/CRC Press, ISBN 978-1568811307, OCLC  316054929
  2. ^ ab Kiyomi, M.; Matsui, T. (2001), "Algoritmos basados ​​en programación de enteros para problemas de solitario de clavijas", Proc. 2nd Int. Conf. Computers and Games (CG 2000): Algoritmos basados ​​en programación de enteros para problemas de solitario de clavijas , Lecture Notes in Computer Science, vol. 2063, págs. 229–240, CiteSeerX 10.1.1.65.6244 , doi :10.1007/3-540-45579-5_15, ISBN  978-3-540-43080-3
  3. ^ Uehara, R.; Iwata, S. (1990). "El Hi-Q generalizado es NP-completo". Trans. IEICE . 73 : 270–273.
  4. ^ Avis, D. ; Deza, A. (2001), "Sobre el cono solitario y su relación con los flujos de múltiples productos", Programación matemática , 90 (1): 27–57, doi :10.1007/PL00011419, S2CID  7852133
  5. ^ Eichler; Jäger; Ludwig (1999), c't 07/1999 Spielverderber, Solitaire mit dem Computer lösen (en alemán), vol. 7, pág. 218
  6. ^ "Matemáticas y brainvita", Notas sobre matemáticas , 28 de agosto de 2012 , consultado el 6 de septiembre de 2018
  7. ^ Para la prueba de Beasley, véase Winning Ways , volumen n.° 4 (segunda edición).
  8. ^ "solboard". github . 2020-08-31 . Consultado el 2020-08-31 . Implementación del cálculo de fuerza bruta del juego de solitario Peg
  9. ^ Brassine, Michel (diciembre de 1981), "Découvrez... le solitaire", Jeux et Stratégie (en francés)
  10. ^ Ver Tableros cruzados generalizados en: Página de George's Peg Solitaire

Lectura adicional

  • Beasley, John D. (1985), Los entresijos del solitario Peg , Oxford University Press , ISBN 978-0198532033
  • Bell, GI (2008), "Resolución del solitario de clavijas triangulares", Journal of Integer Sequences , 11 : Artículo 08.4.8, arXiv : math.CO/0703865 , Bibcode :2007math......3865B.
  • Bruijn, NG de (1972), "Un juego de solitario y su relación con un campo finito" (PDF) , Journal of Recreational Mathematics , 5 : 133–137, archivado (PDF) desde el original el 2022-10-09
  • Cross, DC (1968), "Solitario cuadrado y variaciones", Journal of Recreational Mathematics , 1 : 121–123
  • Gardner, M. , "Juegos matemáticos", Scientific American 206 (6): 156–166, junio de 1962; 214 (2): 112–113, febrero de 1966; 214 (5): 127, mayo de 1966.
  • Jefferson, Chris; et al. (octubre de 2006), "Modelado y resolución del solitario inglés", Computers & Operations Research , 33 (10): 2935–2959, CiteSeerX  10.1.1.5.7805 , doi :10.1016/j.cor.2005.01.018
Wikimedia Commons alberga una categoría multimedia sobre Peg solitaire .
  • Bogomolny, Alexander, "Peg Solitaire and Group Theory", Interactive Mathematics Miscellany and Puzzles , consultado el 7 de septiembre de 2018
  • White Pixels (24 de octubre de 2017), Peg Solitaire: Solución simétrica fácil de recordar (video), Youtube, archivado del original el 2021-12-11
Obtenido de "https://es.wikipedia.org/w/index.php?title=Peg_solitaire&oldid=1240494392"