Interior (topología)

En matemáticas , específicamente en topología , el interior de un subconjunto S de un espacio topológico X es la unión de todos los subconjuntos de S que son abiertos en X. Un punto que está en el interior de S es un punto interior de S.

El interior de S es el complemento de la clausura del complemento de S. En este sentido, interior y clausura son nociones duales .

El exterior de un conjunto S es el complemento de la clausura de S ; está formado por los puntos que no están ni en el conjunto ni en su borde . El interior, el borde y el exterior de un subconjunto dividen todo el espacio en tres bloques (o menos cuando uno o más de ellos están vacíos ).

El interior y el exterior de una curva cerrada son un concepto ligeramente diferente; consulte el teorema de la curva de Jordan .

Si es un subconjunto de un espacio euclidiano , entonces es un punto interior de si existe una bola abierta centrada en que está completamente contenida en (Esto se ilustra en la sección introductoria de este artículo).${\estilo de visualización S}$${\estilo de visualización x}$${\estilo de visualización S}$${\estilo de visualización x}$${\estilo de visualización S.}$

Esta definición se generaliza a cualquier subconjunto de un espacio métrico con métrica : es un punto interior de si existe un número real tal que está en siempre que la distancia${\estilo de visualización S}$ ${\estilo de visualización X}$${\estilo de visualización d}$${\estilo de visualización x}$${\estilo de visualización S}$${\displaystyle r>0,}$${\estilo de visualización y}$${\estilo de visualización S}$${\displaystyle d(x,y)<r.}$

Esta definición se generaliza a los espacios topológicos reemplazando "bola abierta" por " conjunto abierto ". Si es un subconjunto de un espacio topológico , entonces es un punto interior de en si está contenido en un subconjunto abierto de que está completamente contenido en (Equivalentemente, es un punto interior de si es un entorno de )${\estilo de visualización S}$${\estilo de visualización X}$${\estilo de visualización x}$${\estilo de visualización S}$${\estilo de visualización X}$${\estilo de visualización x}$${\estilo de visualización X}$${\estilo de visualización S.}$${\estilo de visualización x}$${\estilo de visualización S}$${\estilo de visualización S}$${\estilo de visualización x.}$

El interior de un subconjunto de un espacio topológico denotado por o o puede definirse de cualquiera de las siguientes formas equivalentes:${\estilo de visualización S}$${\estilo de visualización X,}$${\displaystyle \nombreoperador {int} _{X}S}$${\displaystyle \nombreoperador {int} S}$${\displaystyle S^{\circ },}$

1. ${\displaystyle \nombreoperador {int} S}$es el subconjunto abierto más grande contenido en${\estilo de visualización X}$${\estilo de visualización S.}$
2. ${\displaystyle \nombreoperador {int} S}$es la unión de todos los conjuntos abiertos de contenidos en${\estilo de visualización X}$${\estilo de visualización S.}$
3. ${\displaystyle \nombreoperador {int} S}$es el conjunto de todos los puntos interiores de${\estilo de visualización S.}$

Si el espacio se entiende a partir del contexto, generalmente se prefiere la notación más corta.${\estilo de visualización X}$${\displaystyle \nombreoperador {int} S}$${\displaystyle \operatorname {int}_{X}S.}$

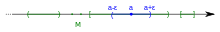
• En cualquier espacio, el interior del conjunto vacío es el conjunto vacío.
• En cualquier espacio si entonces${\estilo de visualización X,}$${\displaystyle S\subseteq X,}$${\displaystyle \operatorname {int} S\subseteq S.}$
• Si es la recta real (con la topología estándar), entonces mientras que el interior del conjunto de números racionales está vacío:${\estilo de visualización X}$ ${\displaystyle \mathbb {R}}$${\displaystyle \operatorname {int} ([0,1])=(0,1)}$${\displaystyle \mathbb {Q}}$${\displaystyle \operatorname {int} \mathbb {Q} =\varnothing .}$
• Si es el plano complejo entonces${\estilo de visualización X}$ ${\displaystyle \mathbb {C} ,}$${\displaystyle \operatorname {int} (\{z\in \mathbb {C} :|z|\leq 1\})=\{z\in \mathbb {C} :|z|<1\}.}$
• En cualquier espacio euclidiano , el interior de cualquier conjunto finito es el conjunto vacío.

En el conjunto de números reales se pueden poner otras topologías distintas a la estándar:

• Si son los números reales con la topología de límite inferior , entonces${\estilo de visualización X}$${\displaystyle \mathbb {R}}$${\displaystyle \operatorname {int} ([0,1])=[0,1).}$
• Si se considera la topología en la que cada conjunto es abierto , entonces${\displaystyle \mathbb {R} }$${\displaystyle \operatorname {int} ([0,1])=[0,1].}$
• Si se considera la topología en la que los únicos conjuntos abiertos son el conjunto vacío y él mismo, entonces es el conjunto vacío.${\displaystyle \mathbb {R} }$${\displaystyle \mathbb {R} }$${\displaystyle \operatorname {int} ([0,1])}$

Estos ejemplos muestran que el interior de un conjunto depende de la topología del espacio subyacente. Los dos últimos ejemplos son casos especiales de lo siguiente.

• En cualquier espacio discreto , como todo conjunto es abierto, todo conjunto es igual a su interior.
• En cualquier espacio indiscreto ya que los únicos conjuntos abiertos son el conjunto vacío y él mismo, y para cada subconjunto propio de es el conjunto vacío.${\displaystyle X,}$${\displaystyle X}$${\displaystyle \operatorname {int} X=X}$ ${\displaystyle S}$${\displaystyle X,}$ ${\displaystyle \operatorname {int} S}$

Sea un espacio topológico y sean y subconjuntos de${\displaystyle X}$${\displaystyle S}$${\displaystyle T}$${\displaystyle X.}$

• ${\displaystyle \operatorname {int} S}$está abierto en${\displaystyle X.}$
• Si está abierto entonces si y sólo si${\displaystyle T}$${\displaystyle X}$${\displaystyle T\subseteq S}$${\displaystyle T\subseteq \operatorname {int} S.}$
• ${\displaystyle \operatorname {int} S}$es un subconjunto abierto de cuando se da la topología del subespacio .${\displaystyle S}$${\displaystyle S}$
• ${\displaystyle S}$es un subconjunto abierto de si y solo si${\displaystyle X}$ ${\displaystyle \operatorname {int} S=S.}$
• Intensivo :${\displaystyle \operatorname {int} S\subseteq S.}$
• Idempotencia :${\displaystyle \operatorname {int} (\operatorname {int} S)=\operatorname {int} S.}$
• Conserva / distribuye sobre la intersección binaria :${\displaystyle \operatorname {int} (S\cap T)=(\operatorname {int} S)\cap (\operatorname {int} T).}$
  • Sin embargo, el operador interior no distribuye entre uniones ya que solo está garantizado en general y la igualdad podría no cumplirse. ^{[nota 1]} Por ejemplo, si y entonces es un subconjunto propio de${\displaystyle \operatorname {int} (S\cup T)~\supseteq ~(\operatorname {int} S)\cup (\operatorname {int} T)}$${\displaystyle X=\mathbb {R} ,S=(-\infty ,0],}$${\displaystyle T=(0,\infty )}$${\displaystyle (\operatorname {int} S)\cup (\operatorname {int} T)=(-\infty ,0)\cup (0,\infty )=\mathbb {R} \setminus \{0\}}$${\displaystyle \operatorname {int} (S\cup T)=\operatorname {int} \mathbb {R} =\mathbb {R} .}$
• Monótona / no decreciente con respecto a${\displaystyle \subseteq }$ : Si entonces${\displaystyle S\subseteq T}$${\displaystyle \operatorname {int} S\subseteq \operatorname {int} T.}$

Otras propiedades incluyen:

• Si está cerrado y entonces${\displaystyle S}$${\displaystyle X}$${\displaystyle \operatorname {int} T=\varnothing }$${\displaystyle \operatorname {int} (S\cup T)=\operatorname {int} S.}$

Relación con el cierre

Las afirmaciones anteriores seguirán siendo verdaderas si todas las instancias de los símbolos/palabras

"interior", "int", "abierto", "subconjunto" y "más grande"

se sustituyen respectivamente por

" cierre ", "cl", "cerrado", "superconjunto" y "más pequeño"

y se intercambian los siguientes símbolos:

1. " " intercambiado con " "${\displaystyle \subseteq }$${\displaystyle \supseteq }$
2. " " intercambiado con " "${\displaystyle \cup }$${\displaystyle \cap }$

Para más detalles sobre este asunto, véase el operador interior a continuación o el artículo Axiomas de cierre de Kuratowski .

El operador interior es dual al operador de clausura , que se denota por o por una barra invertida ^— , en el sentido de que y también donde es el espacio topológico que contiene y la barra invertida denota la diferencia de la teoría de conjuntos . Por lo tanto, la teoría abstracta de los operadores de clausura y los axiomas de clausura de Kuratowski se pueden traducir fácilmente al lenguaje de los operadores interiores, reemplazando los conjuntos con sus complementos en${\displaystyle \operatorname {int} _{X}}$${\displaystyle \operatorname {cl} _{X}}$$${\displaystyle \operatorname {int} _{X}S=X\setminus {\overline {(X\setminus S)}}}$$$${\displaystyle {\overline {S}}=X\setminus \operatorname {int} _{X}(X\setminus S),}$$${\displaystyle X}$${\displaystyle S,}$${\displaystyle \,\setminus \,}$${\displaystyle X.}$

En general, el operador interior no conmuta con las uniones. Sin embargo, en un espacio métrico completo, se cumple el siguiente resultado:

El resultado anterior implica que todo espacio métrico completo es un espacio de Baire .

El exterior de un subconjunto de un espacio topológico denotado por o simplemente es el conjunto abierto más grande disjunto de es decir, es la unión de todos los conjuntos abiertos en que son disjuntos de El exterior es el interior del complemento, que es el mismo que el complemento del cierre; ^[2] en fórmulas,${\displaystyle S}$${\displaystyle X,}$${\displaystyle \operatorname {ext} _{X}S}$${\displaystyle \operatorname {ext} S,}$${\displaystyle S,}$${\displaystyle X}$${\displaystyle S.}$$${\displaystyle \operatorname {ext} S=\operatorname {int} (X\setminus S)=X\setminus {\overline {S}}.}$$

De manera similar, el interior es el exterior del complemento:$${\displaystyle \operatorname {int} S=\operatorname {ext} (X\setminus S).}$$

El interior, el límite y el exterior de un conjunto dividen todo el espacio en tres bloques (o menos cuando uno o más de ellos están vacíos): donde denota el límite de ^[3] El interior y el exterior siempre están abiertos , mientras que el límite está cerrado .${\displaystyle S}$$${\displaystyle X=\operatorname {int} S\cup \partial S\cup \operatorname {ext} S,}$$${\displaystyle \partial S}$${\displaystyle S.}$

Algunas de las propiedades del operador exterior son diferentes a las del operador interior:

• El operador exterior invierte las inclusiones; si entonces${\displaystyle S\subseteq T,}$${\displaystyle \operatorname {ext} T\subseteq \operatorname {ext} S.}$
• El operador exterior no es idempotente . Tiene la propiedad de que${\displaystyle \operatorname {int} S\subseteq \operatorname {ext} \left(\operatorname {ext} S\right).}$

Dos formas y se denominan disjuntas interiores si la intersección de sus interiores está vacía. Las formas disjuntas interiores pueden o no intersecarse en su límite.${\displaystyle a}$${\displaystyle b}$

• Interior algebraico  – Generalización del interior topológico
• DE-9IM  – Modelo topológico
• Álgebra interior  – Estructura algebraica
• Teorema de la curva de Jordan  : una curva cerrada divide el plano en dos regiones
• Interior cuasi-relativo  – Generalización del interior algebraico
• Interior relativo  – Generalización del interior topológico

• Bourbaki, Nicolás (1989) [1966]. Topología general: capítulos 1 a 4 [ Topologie Générale ]. Elementos matemáticos . Berlín Nueva York: Springer Science & Business Media. ISBN 978-3-540-64241-1.OCLC 18588129  .
• Dixmier, Jacques (1984). Topología general . Textos de pregrado en matemáticas. Traducido por Berberian, SK. Nueva York: Springer-Verlag . ISBN. 978-0-387-90972-1.OCLC 10277303  .
• Császár, Ákos (1978). Topología general . Traducido por Császár, Klára. Bristol Inglaterra: Adam Hilger Ltd. ISBN 0-85274-275-4.OCLC 4146011  .
• Dugundji, James (1966). Topología . Boston: Allyn and Bacon. ISBN 978-0-697-06889-7.OCLC 395340485  .
• Joshi, KD (1983). Introducción a la topología general . Nueva York: John Wiley and Sons Ltd. ISBN 978-0-85226-444-7.OCLC 9218750  .
• Kelley, John L. (1975). Topología general . Textos de posgrado en matemáticas . Vol. 27. Nueva York: Springer Science & Business Media. ISBN 978-0-387-90125-1.OCLC 338047  .
• Munkres, James R. (2000). Topología (segunda edición). Upper Saddle River, NJ : Prentice Hall, Inc. ISBN 978-0-13-181629-9.OCLC 42683260  .
• Schubert, Horst (1968). Topología . Londres: Macdonald & Co. ISBN 978-0-356-02077-8.OCLC 463753  .
• Wilansky, Albert (17 de octubre de 2008) [1970]. Topología para análisis . Mineola, Nueva York: Dover Publications, Inc. ISBN 978-0-486-46903-4.OCLC 227923899  .
• Willard, Stephen (2004) [1970]. Topología general. Mineola, NY : Dover Publications . ISBN 978-0-486-43479-7.OCLC 115240  .

• Interior en PlanetMath .