HSL y HSV

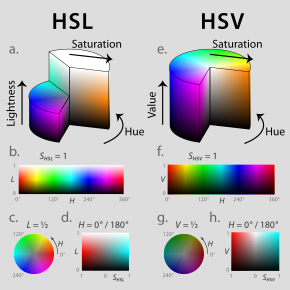
HSL y HSV son las dos representaciones de puntos en coordenadas cilíndricas más comunes en un modelo de color RGB . Las dos representaciones reorganizan la geometría de RGB en un intento de ser más intuitivas y perceptualmente relevantes que la representación cartesiana (cubo). Desarrolladas en la década de 1970 para aplicaciones de gráficos de computadora , HSL y HSV se utilizan hoy en día en selectores de color , en software de edición de imágenes y, con menos frecuencia, en análisis de imágenes y visión artificial .

HSL significa tono , saturación y luminosidad , y a menudo también se lo llama HLS . HSV significa tono , saturación y valor , y a menudo también se lo llama HSB ( B de brillo ). Un tercer modelo, común en aplicaciones de visión artificial, es HSI , para tono , saturación e intensidad . Sin embargo, aunque generalmente son consistentes, estas definiciones no están estandarizadas y cualquiera de estas abreviaturas podría usarse para cualquiera de estos tres o varios otros modelos cilíndricos relacionados. (Para las definiciones técnicas de estos términos, consulte a continuación).

En cada cilindro, el ángulo alrededor del eje vertical central corresponde al " tono ", la distancia desde el eje corresponde a la " saturación " y la distancia a lo largo del eje corresponde a la " luminosidad ", el "valor" o el " brillo ". Nótese que, si bien "tono" en HSL y HSV se refiere al mismo atributo, sus definiciones de "saturación" difieren drásticamente. Debido a que HSL y HSV son transformaciones simples de modelos RGB dependientes del dispositivo, los colores físicos que definen dependen de los colores de los primarios rojo, verde y azul del dispositivo o del espacio RGB particular, y de la corrección gamma utilizada para representar las cantidades de esos primarios. Por lo tanto, cada dispositivo RGB único tiene espacios HSL y HSV únicos que lo acompañan, y los valores numéricos HSL o HSV describen un color diferente para cada espacio RGB base. ^[1]

Ambas representaciones se utilizan ampliamente en gráficos por ordenador y una de ellas suele ser más conveniente que la RGB, pero ambas reciben críticas por no separar adecuadamente los atributos que determinan el color o por su falta de uniformidad perceptual. Se dice que otros modelos que requieren más recursos computacionales, como CIELAB o CIECAM02, logran mejor estos objetivos.

Tanto HSL como HSV son geometrías cilíndricas ( fig. 2 ), con tono, su dimensión angular, comenzando en el primario rojo a 0°, pasando por el primario verde a 120° y el primario azul a 240°, y luego envolviendo nuevamente al rojo a 360°. En cada geometría, el eje vertical central comprende los colores neutros , acromáticos o grises que van, de arriba a abajo, desde el blanco en luminosidad 1 (valor 1) hasta el negro en luminosidad 0 (valor 0).

En ambas geometrías, los colores primarios y secundarios aditivos (rojo, amarillo , verde, cian , azul y magenta ) y las mezclas lineales entre pares adyacentes de ellos, a veces llamados colores puros , se disponen alrededor del borde exterior del cilindro con saturación 1. Estos colores saturados tienen luminosidad 0,5 en HSL, mientras que en HSV tienen valor 1. Mezclar estos colores puros con negro (produciendo los llamados tonos ) deja la saturación sin cambios. En HSL, la saturación también se mantiene sin cambios al teñir con blanco, y solo las mezclas con negro y blanco (llamadas tonos ) tienen saturación menor a 1. En HSV, el teñido solo reduce la saturación.

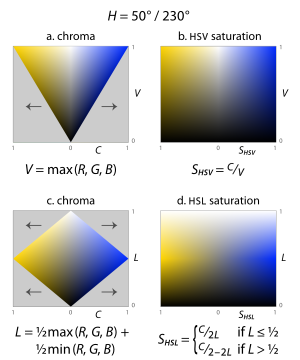
Debido a que estas definiciones de saturación, en las que los colores casi neutros muy oscuros (en ambos modelos) o muy claros (en HSL) se consideran completamente saturados (por ejemplo, desde la parte inferior derecha en el cilindro HSL cortado o desde la parte superior derecha) – entra en conflicto con la noción intuitiva de pureza de color, a menudo se dibuja en su lugar un sólido cónico o bicónico ( fig. 3 ), con lo que este artículo llama croma como su dimensión radial (igual al rango de los valores RGB), en lugar de saturación (donde la saturación es igual al croma sobre el croma máximo en esa porción del (bi)cono). De manera confusa, dichos diagramas suelen etiquetar esta dimensión radial como "saturación", difuminando o borrando la distinción entre saturación y croma. ^[A] Como se describe a continuación, calcular el croma es un paso útil en la derivación de cada modelo. Debido a que un modelo intermedio de este tipo, con dimensiones de tono, croma y valor HSV o luminosidad HSL, toma la forma de un cono o bicono, HSV a menudo se denomina "modelo de hexcono", mientras que HSL a menudo se denomina "modelo de bi-hexcono" (fig. 8). ^[B]

La mayoría de los televisores, pantallas de ordenador y proyectores producen colores combinando luz roja, verde y azul en intensidades variables: los denominados colores primarios aditivos RGB . Las mezclas resultantes en el espacio de color RGB pueden reproducir una amplia variedad de colores (lo que se denomina gama ); sin embargo, la relación entre las cantidades constituyentes de luz roja, verde y azul y el color resultante no es intuitiva, especialmente para usuarios inexpertos y para usuarios familiarizados con la mezcla sustractiva de colores de pinturas o los modelos tradicionales de artistas basados ​​en tintes y sombras ( fig. 4 ). Además, ni los modelos de color aditivos ni los sustractivos definen las relaciones de color de la misma manera que lo hace el ojo humano . ^[C]

Por ejemplo, imaginemos que tenemos una pantalla RGB cuyo color se controla mediante tres controles deslizantes que van de 0 a 255 , y uno de ellos controla la intensidad de cada uno de los colores primarios rojo, verde y azul. Si comenzamos con un naranja relativamente colorido  , con valores sRGB R = 217 , G = 118 , B = 33 , y desea reducir su colorido a la mitad a un naranja menos saturado , necesitaríamos arrastrar los controles deslizantes para disminuir R en 31, aumentar G en 24 y aumentar B en 59, como se muestra en la siguiente imagen.

A partir de la década de 1950, las transmisiones de televisión en color utilizaron un sistema de color compatible mediante el cual las señales de " luminancia " y " crominancia " se codificaban por separado, de modo que los televisores en blanco y negro sin modificar existentes aún podían recibir transmisiones en color y mostrar una imagen monocromática. ^[9]

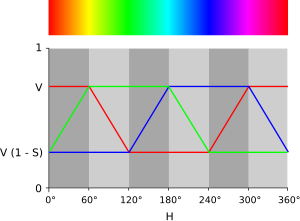
En un intento de dar cabida a modelos de mezcla de colores más tradicionales e intuitivos, los pioneros de los gráficos por ordenador de PARC y NYIT introdujeron el modelo HSV para la tecnología de visualización de ordenadores a mediados de los años 1970, descrito formalmente por Alvy Ray Smith ^[10] en la edición de agosto de 1978 de Computer Graphics . En la misma edición, Joblove y Greenberg ^[11] describieron el modelo HSL (cuyas dimensiones denominaron tono , croma relativo e intensidad ) y lo compararon con HSV ( fig. 1 ). Su modelo se basaba más en cómo se organizan y conceptualizan los colores en la visión humana en términos de otros atributos que forman el color, como el tono, la luminosidad y el croma; así como en los métodos tradicionales de mezcla de colores (por ejemplo, en pintura) que implican mezclar pigmentos de colores brillantes con negro o blanco para conseguir colores más claros, más oscuros o menos coloridos.

El año siguiente, 1979, en SIGGRAPH , Tektronix presentó terminales gráficas que utilizaban HSL para la designación de colores, y el Comité de Estándares de Gráficos de Computadora lo recomendó en su informe de situación anual ( fig. 7 ). Estos modelos eran útiles no solo porque eran más intuitivos que los valores RGB sin procesar, sino también porque las conversiones hacia y desde RGB eran extremadamente rápidas de calcular: podían ejecutarse en tiempo real en el hardware de la década de 1970. En consecuencia, estos modelos y otros similares se han vuelto omnipresentes en todo el software de edición de imágenes y gráficos desde entonces. Algunos de sus usos se describen a continuación. ^{[12] [13] [14] [15]}

Las dimensiones de las geometrías HSL y HSV (simples transformaciones del modelo RGB no basado en la percepción) no están directamente relacionadas con los atributos fotométricos de formación de color de los mismos nombres, tal como los definen científicos como la CIE o ASTM . No obstante, vale la pena revisar esas definiciones antes de pasar a la derivación de nuestros modelos. ^[D] Para las definiciones de los atributos de formación de color que aparecen a continuación, consulte: ^{[16] [17] [18] [19] [20] [21]}

Matiz

"El "atributo de una sensación visual según el cual un área parece ser similar a uno de los colores percibidos : rojo, amarillo, verde y azul, o a una combinación de dos de ellos". ^[16]

Radiancia ( L _e,Ω )

La potencia radiante de la luz que pasa a través de una superficie particular por unidad de ángulo sólido por unidad de área proyectada, medida en unidades del SI en vatios por estereorradián por metro cuadrado ( W·sr ⁻¹ ·m ⁻² ).

Luminancia ( Y o L _v,Ω )

Radiancia ponderada por el efecto de cada longitud de onda en un observador humano típico, medida en unidades del SI en _candelas por metro cuadrado ( cd/m2 ⁾ . A menudo se utiliza el término luminancia para la luminancia relativa , Y / Yn , donde Yn es la luminancia del punto blanco de _referencia .

Luminosidad ( Y ′ )

La suma ponderada de los valores R ′ , G ′ y B ′ corregidos por gamma , y ​​se utiliza en Y ′ CbCr , para la compresión JPEG y la transmisión de vídeo.

Brillo (o valor)

El "atributo de una sensación visual según el cual un área parece emitir más o menos luz". ^[16]

Ligereza

El "brillo relativo al brillo de un blanco iluminado de manera similar". ^[16]

Colorido

El "atributo de una sensación visual según el cual el color percibido de un área parece ser más o menos cromático". ^[16]

Croma

El "colorido relativo al brillo de un blanco iluminado de manera similar". ^[16]

Saturación

El "colorido de un estímulo en relación con su propio brillo". ^[16]

El brillo y el colorido son medidas absolutas que suelen describir la distribución espectral de la luz que entra en el ojo, mientras que la luminosidad y el croma se miden en relación con un punto blanco y, por lo tanto, se utilizan a menudo para describir los colores de la superficie, permaneciendo aproximadamente constantes incluso cuando el brillo y el colorido cambian con diferentes niveles de iluminación . La saturación se puede definir como la relación entre el colorido y el brillo o entre el croma y la luminosidad.

Los modelos HSL, HSV y otros relacionados pueden derivarse mediante estrategias geométricas o pueden considerarse como instancias específicas de un "modelo LHS generalizado". Los creadores de los modelos HSL y HSV tomaron un cubo RGB (con cantidades constituyentes de luz roja, verde y azul en un color denotado R , G , B ∈ [0, 1] ^[E] ) y lo inclinaron sobre su esquina, de modo que el negro descansara en el origen con el blanco directamente encima de él a lo largo del eje vertical, luego midieron el tono de los colores en el cubo por su ángulo alrededor de ese eje, comenzando con el rojo a 0°. Luego idearon una caracterización de brillo/valor/luminosidad y definieron la saturación para que oscilara entre 0 a lo largo del eje y 1 en el punto más colorido para cada par de otros parámetros. ^{[2] [10] [11]}

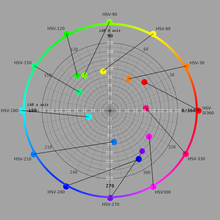
En cada uno de nuestros modelos, calculamos tanto el tono como lo que este artículo llamará croma , en honor a Joblove y Greenberg (1978), de la misma manera; es decir, el tono de un color tiene los mismos valores numéricos en todos estos modelos, al igual que su croma. Si tomamos nuestro cubo RGB inclinado y lo proyectamos sobre el " plano de cromaticidad " perpendicular al eje neutro, nuestra proyección toma la forma de un hexágono, con rojo, amarillo, verde, cian, azul y magenta en sus esquinas ( fig. 9 ). El tono es aproximadamente el ángulo del vector con respecto a un punto en la proyección, con el rojo a 0°, mientras que el croma es aproximadamente la distancia del punto desde el origen. ^{[F] [G]}

Más precisamente, tanto el tono como el croma en este modelo se definen con respecto a la forma hexagonal de la proyección. El croma es la proporción de la distancia desde el origen hasta el borde del hexágono. En la parte inferior del diagrama adyacente, esta es la relación de las longitudes OP / OP ′ o, alternativamente, la relación de los radios de los dos hexágonos. Esta relación es la diferencia entre los valores más grande y más pequeño entre R , G o B en un color. Para que nuestras definiciones sean más fáciles de escribir, definiremos estos valores máximos, mínimos y de componente de croma como M , m y C , respectivamente. ^[H]

${\displaystyle M=\max(R,G,B)}$

${\displaystyle m=\min(R,G,B)}$

${\displaystyle C=\operatorname {rango} (R,G,B)=Mm}$

Para entender por qué el croma se puede escribir como M − m , observe que cualquier color neutro, con R = G = B , se proyecta sobre el origen y, por lo tanto, tiene un croma 0. Por lo tanto, si sumamos o restamos la misma cantidad de los tres, R , G y B , nos movemos verticalmente dentro de nuestro cubo inclinado y no cambiamos la proyección. Por lo tanto, dos colores cualesquiera de ( R , G , B ) y ( R − m , G − m , B − m ) se proyectan en el mismo punto y tienen el mismo croma. El croma de un color con uno de sus componentes igual a cero ( m = 0) es simplemente el máximo de los otros dos componentes. Este croma es M en el caso particular de un color con un componente cero y M − m en general.

El tono es la proporción de la distancia alrededor del borde del hexágono que pasa por el punto proyectado, originalmente medido en el rango [0, 1] pero ahora medido típicamente en grados [0°, 360°) . Para los puntos que se proyectan sobre el origen en el plano de cromaticidad (es decir, grises), el tono no está definido. Matemáticamente, esta definición de tono se escribe por partes : ^[I]

${\displaystyle H'={\begin{cases}\mathrm {undefined} ,&{\text{si }}C=0\\{\frac {GB}{C}}{\bmod {6}},&{\text{si }}M=R\\{\frac {BR}{C}}+2,&{\text{si }}M=G\\{\frac {RG}{C}}+4,&{\text{si }}M=B\end{cases}}}$

${\displaystyle H=60^{\circ }\times H'}$

A veces, a los colores neutros (es decir, con C = 0 ) se les asigna un tono de 0° para facilitar la representación.

Estas definiciones equivalen a una deformación geométrica de los hexágonos en círculos: cada lado del hexágono se proyecta linealmente sobre un arco de 60° del círculo ( fig. 10 ). Después de dicha transformación, el tono es precisamente el ángulo alrededor del origen y el croma la distancia desde el origen: el ángulo y la magnitud del vector que apunta a un color.

A veces, para aplicaciones de análisis de imágenes, se omite esta transformación de hexágono a círculo y el tono y el croma (los llamaremos H ₂ y C ₂ ) se definen mediante las transformaciones de coordenadas cartesianas a polares habituales ( fig. 11 ). La forma más fácil de derivarlas es mediante un par de coordenadas de cromaticidad cartesianas que llamaremos α y β : ^{[22] [23] [24]}

${\displaystyle \alpha =RG\cdot \cos(60^{\circ })-B\cdot \cos(60^{\circ })={\tfrac {1}{2}}(2R-GB)}$

${\displaystyle \beta =G\cdot \sin(60^{\circ })-B\cdot \sin(60^{\circ })={\tfrac {\sqrt {3}}{2}}(GB )}$

${\displaystyle H_{2}=\nombre del operador {atan2} (\beta ,\alpha )}$

${\displaystyle C_{2}=\operatorname {gmean} (\alpha ,\beta )={\sqrt {\alpha ^{2}+\beta ^{2}}}}$

(La función atan2 , una "arcotangente de dos argumentos", calcula el ángulo a partir de un par de coordenadas cartesianas).

Nótese que estas dos definiciones de tono ( H y H ₂ ) casi coinciden, con una diferencia máxima entre ellas para cualquier color de aproximadamente 1,12° – lo que ocurre en doce tonos particulares, por ejemplo H = 13,38° , H ₂ = 12,26° – y con H = H ₂ para cada múltiplo de 30°. Las dos definiciones de croma ( C y C ₂ ) difieren más sustancialmente: son iguales en los vértices de nuestro hexágono, pero en puntos a medio camino entre dos vértices, como H = H ₂ = 30° , tenemos C = 1 , pero una diferencia de aproximadamente 13,4%.${\textstyle C_{2}={\sqrt {\frac {3}{4}}}\aproximadamente 0,866,}$

Si bien la definición de tono es relativamente indiscutible (satisface aproximadamente el criterio de que los colores del mismo tono percibido deben tener el mismo tono numérico), la definición de una dimensión de luminosidad o valor es menos obvia: existen varias posibilidades según el propósito y los objetivos de la representación. A continuación se presentan cuatro de las más comunes ( fig. 12 ; tres de ellas también se muestran en la fig. 8):

• La definición más simple es simplemente la media aritmética , es decir, el promedio, de los tres componentes, en el modelo HSI llamado intensidad ( fig. 12a ). Esto es simplemente la proyección de un punto sobre el eje neutro: la altura vertical de un punto en nuestro cubo inclinado. La ventaja es que, junto con los cálculos de distancia euclidiana de tono y croma, esta representación conserva las distancias y los ángulos de la geometría del cubo RGB. ^{[23] [25]}

  ${\displaystyle I=\operatorname {avg} (R,G,B)={\tfrac {1}{3}}(R+G+B)}$

• En el modelo de "cono hexagonal" HSV, el valor se define como el componente más grande de un color, nuestra M anterior ( fig. 12b ). Esto coloca los tres colores primarios, y también todos los "colores secundarios" (cian, amarillo y magenta) en un plano con el blanco, formando una pirámide hexagonal a partir del cubo RGB. ^[10]

  ${\displaystyle V=\max(R,G,B)=M}$

• En el modelo "bi-hexcone" de HSL, la luminosidad se define como el promedio de los componentes de color más grandes y más pequeños ( fig. 12c ), es decir, el rango medio de los componentes RGB. Esta definición también coloca los colores primarios y secundarios en un plano, pero un plano que pasa a mitad de camino entre el blanco y el negro. El sólido de color resultante es un cono doble similar al de Ostwald, que se muestra arriba. ^[11]

  ${\displaystyle L=\operatorname {mid} (R,G,B)={\tfrac {1}{2}}(M+m)}$

• Una alternativa más relevante desde el punto de vista perceptual es utilizar luma , Y ′ , como dimensión de luminosidad ( fig. 12d ). Luma es el promedio ponderado de R , G y B corregidos por gamma , en función de su contribución a la luminosidad percibida, que se ha utilizado durante mucho tiempo como dimensión monocromática en la transmisión de televisión en color. Para sRGB , los primarios Rec. 709 dan como resultado Y ′ ₇₀₉ , el NTSC digital utiliza Y ′ ₆₀₁ según Rec. 601 y también se utilizan algunos otros primarios que dan como resultado coeficientes diferentes. ^{[26] [J]}

  ${\displaystyle Y'_{\text{601}}=0,299\cdot R+0,587\cdot G+0,114\cdot B}$(televisión de definición estándar)

  ${\displaystyle Y'_{\text{240}}=0,212\cdot R+0,701\cdot G+0,087\cdot B}$ (Adobe)

  ${\displaystyle Y'_{\text{709}}=0,2126\cdot R+0,7152\cdot G+0,0722\cdot B}$ (televisión de alta definición)

  ${\displaystyle Y'_{\text{2020}}=0,2627\cdot R+0,6780\cdot G+0,0593\cdot B}$ (UHDTV, HDR)

Los cuatro dejan intacto el eje neutro. Es decir, para colores con R = G = B , cualquiera de las cuatro formulaciones produce una luminosidad igual al valor de R , G o B.

Para una comparación gráfica, consulte la figura 13 a continuación.

Al codificar colores en un modelo de tono/luminosidad/croma o tono/valor/croma (usando las definiciones de las dos secciones anteriores), no todas las combinaciones de luminosidad (o valor) y croma son significativas: es decir, la mitad de los colores denotables usando H ∈ [0°, 360°) , C ∈ [0, 1] y V ∈ [0, 1] quedan fuera de la gama RGB (las partes grises de los cortes en la figura 14). Los creadores de estos modelos consideraron que esto era un problema para algunos usos. Por ejemplo, en una interfaz de selección de color con dos de las dimensiones en un rectángulo y la tercera en un control deslizante, la mitad de ese rectángulo está hecha de espacio no utilizado. Ahora imaginemos que tenemos un control deslizante para la luminosidad: la intención del usuario al ajustar este control deslizante es potencialmente ambigua: ¿cómo debería el software manejar los colores fuera de la gama? O a la inversa, si el usuario ha seleccionado un violeta oscuro lo más colorido posible, y luego desplaza el control deslizante de luminosidad hacia arriba. ¿Qué se debe hacer? ¿Preferiría el usuario ver un violeta más claro pero lo más colorido posible para el tono y la luminosidad dados? , o un púrpura más claro de exactamente el mismo croma que el color original ? ^[11]

Para resolver problemas como estos, los modelos HSL y HSV escalan el croma de modo que siempre se ajuste al rango [0, 1] para cada combinación de tono y luminosidad o valor, llamando al nuevo atributo saturación en ambos casos (fig. 14). Para calcular cualquiera de los dos, simplemente hay que dividir el croma por el croma máximo para ese valor o luminosidad.

${\displaystyle S_{V}={\begin{cases}0,&{\text{si }}V=0\\{\frac {C}{V}},&{\text{en caso contrario}}\end{cases}}}$

${\displaystyle S_{L}={\begin{cases}0,&{\text{si }}L=1{\text{ o }}L=0\\{\frac {C}{1-|2L-1|}},&{\text{en caso contrario}}\end{cases}}}$

El modelo HSI que se utiliza habitualmente en la visión artificial, que toma H2 como dimensión de tono y el componente promedio _I ( "intensidad") como dimensión de luminosidad, no intenta "llenar" un cilindro mediante su definición de saturación. En lugar de presentar interfaces de elección o modificación de color a los usuarios finales, el objetivo de HSI es facilitar la separación de formas en una imagen. Por lo tanto, la saturación se define de acuerdo con la definición psicométrica: croma en relación con la luminosidad ( fig. 15 ). Consulte la sección Uso en análisis de imágenes de este artículo. ^[28]

${\displaystyle S_{I}={\begin{cases}0,&{\text{si }}I=0\\1-{\frac {m}{I}},&{\text{en caso contrario}}\end{cases}}}$

El uso del mismo nombre para estas tres definiciones diferentes de saturación genera cierta confusión, ya que los tres atributos describen relaciones de color sustancialmente diferentes; en HSV y HSI, el término coincide aproximadamente con la definición psicométrica, de un croma de un color en relación con su propia luminosidad, pero en HSL no se acerca. Peor aún, la palabra saturación también se usa a menudo para una de las mediciones que llamamos croma anteriormente ( C o C ₂ ).

Todos los valores de los parámetros que se muestran a continuación se dan como valores en el intervalo [0, 1] , excepto los de H y H ₂ , que están en el intervalo [0°, 360°) . ^[K]

El propósito original de HSL y HSV y modelos similares, y su aplicación actual más común, es en herramientas de selección de color . En su forma más simple, algunos de estos selectores de color proporcionan tres controles deslizantes, uno para cada atributo. La mayoría, sin embargo, muestra una sección bidimensional a través del modelo, junto con un control deslizante que controla qué sección en particular se muestra. El último tipo de GUI exhibe una gran variedad, debido a la elección de cilindros, prismas hexagonales o conos/bicones que sugieren los modelos (vea el diagrama cerca de la parte superior de la página). Varios selectores de color de la década de 1990 se muestran a la derecha, la mayoría de los cuales han permanecido casi sin cambios en el tiempo intermedio: hoy, casi todos los selectores de color de computadora usan HSL o HSV, al menos como una opción. Algunas variantes más sofisticadas están diseñadas para elegir conjuntos completos de colores, basando sus sugerencias de colores compatibles en las relaciones HSL o HSV entre ellos. ^[M]

La mayoría de las aplicaciones web que necesitan selección de color también basan sus herramientas en HSL o HSV, y existen selectores de color de código abierto preempaquetados para la mayoría de los principales marcos de interfaz web . La especificación CSS 3 permite a los autores web especificar colores para sus páginas directamente con coordenadas HSL. ^{[N] [29]}

En ocasiones, se utilizan HSL y HSV para definir gradientes para la visualización de datos , como en mapas o imágenes médicas. Por ejemplo, el popular programa SIG ArcGIS aplicaba históricamente gradientes personalizables basados ​​en HSV a datos geográficos numéricos. ^[O]

Fig. 17. Modificador de color basado en HSV de xv .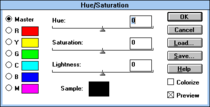

Fig. 18. La herramienta Tono/Saturación en Photoshop 2.5, alrededor de 1992.

El software de edición de imágenes también incluye comúnmente herramientas para ajustar colores con referencia a coordenadas HSL o HSV, o a coordenadas en un modelo basado en la "intensidad" o luma definida anteriormente. En particular, las herramientas con un par de controles deslizantes de "tono" y "saturación" son comunes, y datan al menos de fines de la década de 1980, pero también se han implementado varias herramientas de color más complicadas. Por ejemplo, el visor de imágenes y editor de color de Unix xv permitía rotar y redimensionar seis rangos de tono ( H ) definibles por el usuario , incluía un control tipo dial para la saturación ( S _HSV ) y una interfaz tipo curvas para controlar el valor ( V ); consulte la figura 17. El editor de imágenes Picture Window Pro incluye una herramienta de "corrección de color" que permite reasignar de manera compleja los puntos en un plano de tono/saturación en relación con el espacio HSL o HSV. ^[P]

Los editores de vídeo también utilizan estos modelos. Por ejemplo, tanto Avid como Final Cut Pro incluyen herramientas de color basadas en HSL o una geometría similar para ajustar el color en el vídeo. Con la herramienta de Avid, los usuarios eligen un vector haciendo clic en un punto dentro del círculo de tono/saturación para cambiar todos los colores en un nivel de luminosidad determinado (sombras, tonos medios, luces) según ese vector.

Desde la versión 4.0, los modos de fusión "Luminosidad", "Tono", "Saturación" y "Color" de Adobe Photoshop combinan capas utilizando una geometría de color de luminancia/cromía/tono. Estos modos se han copiado ampliamente, pero varios imitadores utilizan las geometrías HSL (por ejemplo, PhotoImpact , Paint Shop Pro ) o HSV en su lugar. ^{[Q] [R]}

Los modelos HSL, HSV, HSI o relacionados se utilizan a menudo en la visión artificial y el análisis de imágenes para la detección de características o la segmentación de imágenes . Las aplicaciones de estas herramientas incluyen la detección de objetos, por ejemplo, en la visión robótica ; el reconocimiento de objetos , por ejemplo, de rostros , texto o matrículas ; la recuperación de imágenes basada en contenido ; y el análisis de imágenes médicas . ^[28]

En su mayor parte, los algoritmos de visión artificial utilizados en imágenes en color son extensiones sencillas de algoritmos diseñados para imágenes en escala de grises , por ejemplo, k-means o agrupamiento difuso de colores de píxeles, o detección de bordes astuta . En el modo más simple, cada componente de color se pasa por separado a través del mismo algoritmo. Por lo tanto, es importante que las características de interés se puedan distinguir en las dimensiones de color utilizadas. Debido a que los componentes R , G y B del color de un objeto en una imagen digital están todos correlacionados con la cantidad de luz que llega al objeto y, por lo tanto, entre sí, las descripciones de imágenes en términos de esos componentes dificultan la discriminación de objetos. Las descripciones en términos de tono/luminosidad/croma o tono/luminosidad/saturación suelen ser más relevantes. ^[28]

A partir de finales de los años 1970, se utilizaron transformaciones como HSV o HSI como un compromiso entre la eficacia para la segmentación y la complejidad computacional. Se puede pensar que son similares en enfoque e intención al procesamiento neuronal utilizado por la visión del color humana, sin concordar en los detalles: si el objetivo es la detección de objetos, separar aproximadamente el tono, la luminosidad y el croma o la saturación es eficaz, pero no hay ninguna razón particular para imitar estrictamente la respuesta humana al color. La tesis de maestría de John Kender de 1976 propuso el modelo HSI. Ohta et al. (1980) utilizaron en cambio un modelo compuesto de dimensiones similares a las que hemos llamado I , α y β . En los últimos años, estos modelos han seguido siendo ampliamente utilizados, ya que su rendimiento se compara favorablemente con modelos más complejos y su simplicidad computacional sigue siendo convincente. ^{[S] [28] [36] [37] [38]}

Si bien HSL, HSV y otros espacios relacionados sirven lo suficientemente bien como para, por ejemplo, elegir un solo color, ignoran gran parte de la complejidad de la apariencia del color. Esencialmente, sacrifican relevancia perceptual por velocidad de cómputo, desde una época en la historia de la computación (estaciones de trabajo gráficas de alta gama de la década de 1970 o computadoras de escritorio para consumidores de mediados de la década de 1990) en la que los modelos más sofisticados habrían sido demasiado costosos desde el punto de vista computacional. ^[T]

HSL y HSV son transformaciones simples de RGB que conservan simetrías en el cubo RGB no relacionadas con la percepción humana, de modo que sus esquinas R , G y B son equidistantes del eje neutro y están igualmente espaciadas a su alrededor. Si trazamos la gama RGB en un espacio más uniforme desde el punto de vista perceptivo, como CIELAB (ver más abajo), queda inmediatamente claro que los primarios rojo, verde y azul no tienen la misma luminosidad o croma, o tonos espaciados uniformemente. Además, las diferentes pantallas RGB utilizan diferentes primarios y, por lo tanto, tienen diferentes gamas. Debido a que HSL y HSV se definen puramente con referencia a algún espacio RGB, no son espacios de color absolutos : para especificar un color con precisión es necesario informar no solo los valores HSL o HSV, sino también las características del espacio RGB en el que se basan, incluida la corrección gamma en uso.

Si tomamos una imagen y extraemos los componentes de tono, saturación y luminosidad o valor, y luego los comparamos con los componentes del mismo nombre según la definición de los científicos del color, podemos ver rápidamente la diferencia, perceptualmente. Por ejemplo, examine las siguientes imágenes de un tragafuegos ( fig. 13 ). El original está en el espacio de color sRGB. CIELAB L * es una cantidad de luminosidad acromática definida por CIE (que depende únicamente de la luminancia acromática perceptual Y , pero no de los componentes cromáticos mixtos X o Z , del espacio de color CIEXYZ del que se deriva el propio espacio de color sRGB), y es evidente que parece similar en luminosidad perceptual a la imagen de color original. Luma es aproximadamente similar, pero difiere un poco en alto croma, donde se desvía más de depender únicamente de la luminancia acromática verdadera ( Y , o equivalentemente L *) y está influenciada por la cromaticidad colorimétrica ( x, y , o equivalentemente, a*, b* de CIELAB). HSL L y HSV V , por el contrario, divergen sustancialmente de la luminosidad perceptual.

Aunque ninguna de las dimensiones de estos espacios coincide con sus análogos perceptuales, el valor de HSV y la saturación de HSL son particularmente infractores. En HSV, el primario azul y blanco Se considera que ambos tienen el mismo valor, aunque perceptualmente el primario azul tiene alrededor del 10 % de la luminancia del blanco (la fracción exacta depende de los primarios RGB particulares que se utilicen). En HSL, una mezcla de 100 % rojo, 100 % verde, 90 % azul, es decir, un amarillo muy claro – se considera que tiene la misma saturación que el primario verde , aunque el color anterior casi no tiene croma ni saturación según las definiciones psicométricas convencionales. Tales perversidades llevaron a Cynthia Brewer, experta en elección de esquemas de color para mapas y pantallas de información, a decirle a la Asociación Estadounidense de Estadística :

La informática ofrece algunos primos pobres de estos espacios perceptuales que también pueden aparecer en la interfaz de su software, como HSV y HLS. Son transformaciones matemáticas sencillas de RGB y parecen ser sistemas perceptuales porque hacen uso de la terminología de tono-luminosidad/valor-saturación. Pero observe con atención; no se deje engañar. Las dimensiones de color perceptuales están mal escaladas por las especificaciones de color que se proporcionan en estos y algunos otros sistemas. Por ejemplo, la saturación y la luminosidad se confunden, por lo que una escala de saturación también puede contener una amplia gama de luminosidades (por ejemplo, puede progresar del blanco al verde, que es una combinación de luminosidad y saturación). Del mismo modo, el tono y la luminosidad se confunden de modo que, por ejemplo, un amarillo saturado y un azul saturado pueden designarse como la misma "luminosidad", pero tienen amplias diferencias en la luminosidad percibida. Estos defectos hacen que los sistemas sean difíciles de usar para controlar el aspecto de un esquema de color de manera sistemática. Si se requieren muchos ajustes para lograr el efecto deseado, el sistema ofrece pocos beneficios en comparación con lidiar con especificaciones sin procesar en RGB o CMY. ^[39]

Si estos problemas hacen que HSL y HSV sean problemáticos para elegir colores o esquemas de color, los hacen mucho peores para el ajuste de imágenes. HSL y HSV, como mencionó Brewer, confunden los atributos perceptuales de creación de colores, de modo que cambiar cualquier dimensión da como resultado cambios no uniformes en las tres dimensiones perceptuales y distorsiona todas las relaciones de color en la imagen. Por ejemplo, rotar el tono de un azul oscuro puro Hacia el verde También reducirá su croma percibido y aumentará su luminosidad percibida (esta última es más gris y clara), pero la misma rotación de tono tendrá el impacto opuesto en la luminosidad y el croma de un verde azulado más claro. a (este último es más colorido y ligeramente más oscuro). En el ejemplo siguiente ( fig. 21 ), la imagen (a) es la fotografía original de una tortuga verde . En la imagen (b), hemos rotado el tono ( H ) de cada color en −30° , mientras mantenemos constantes el valor HSV y la saturación o la luminosidad y saturación HSL. En la imagen de la derecha (c), realizamos la misma rotación al tono HSL/HSV de cada color, pero luego forzamos a que la luminosidad CIELAB ( L *, una aproximación decente de la luminosidad percibida) permanezca constante. Observe cómo la versión central con el tono desplazado sin dicha corrección cambia drásticamente las relaciones de luminosidad percibida entre los colores de la imagen. En particular, el caparazón de la tortuga es mucho más oscuro y tiene menos contraste, y el agua de fondo es mucho más clara. La imagen (d) utiliza CIELAB para el cambio de tono; la diferencia con (c) demuestra los errores en el tono y la saturación.

Debido a que el tono es una cantidad circular, representada numéricamente con una discontinuidad a 360°, es difícil de usar en cálculos estadísticos o comparaciones cuantitativas: el análisis requiere el uso de estadísticas circulares . ^[40] Además, el tono se define por partes, en fragmentos de 60°, donde la relación de luminosidad, valor y croma con R , G y B depende del fragmento de tono en cuestión. Esta definición introduce discontinuidades, esquinas que se pueden ver claramente en cortes horizontales de HSL o HSV. ^[41]

Charles Poynton, experto en vídeo digital, enumera los problemas mencionados anteriormente con HSL y HSV en sus Preguntas frecuentes sobre color y concluye que:

HSB y HLS se desarrollaron para especificar numéricamente el tono, la saturación y el brillo (o tono, luminosidad y saturación) en una época en la que los usuarios tenían que especificar los colores numéricamente. Las formulaciones habituales de HSB y HLS son erróneas con respecto a las propiedades de la visión del color. Ahora que los usuarios pueden elegir los colores visualmente, o elegir colores relacionados con otros medios (como PANTONE ), o utilizar sistemas basados ​​en la percepción como L*u*v* y L*a*b* , HSB y HLS deberían abandonarse. ^[42]

Los creadores de HSL y HSV no fueron los primeros en imaginar que los colores encajaran en formas cónicas o esféricas, con colores neutros que se extendieran del negro al blanco en un eje central y tonos correspondientes a ángulos alrededor de ese eje. Disposiciones similares datan del siglo XVIII y continúan desarrollándose en los modelos más modernos y científicos.

Para convertir de HSL o HSV a RGB, básicamente invertimos los pasos enumerados anteriormente (como antes, R , G , B ∈ [0, 1] ). Primero, calculamos el croma, multiplicando la saturación por el croma máximo para una luminosidad o valor dado. A continuación, encontramos el punto en una de las tres caras inferiores del cubo RGB que tiene el mismo tono y croma que nuestro color (y, por lo tanto, se proyecta sobre el mismo punto en el plano de cromaticidad). Finalmente, agregamos cantidades iguales de R , G y B para alcanzar la luminosidad o el valor adecuados. ^[G]

Dado un color con tono H ∈ [0°, 360°) , saturación S _L ∈ [0, 1] y luminosidad L ∈ [0, 1] , primero encontramos el croma:

${\displaystyle C=(1-\left\vert 2L-1\right\vert )\times S_{L}}$

Luego podemos encontrar un punto ( R ₁ , G ₁ , B ₁ ) a lo largo de las tres caras inferiores del cubo RGB, con el mismo tono y croma que nuestro color (usando el valor intermedio X para el segundo componente más grande de este color):

${\displaystyle H^{\prime}={\frac {H}{60^{\circ}}}}$

${\displaystyle X=C\times (1-|H^{\prime }\;{\bmod {2}}-1|)}$

En la ecuación anterior, la notación se refiere al resto de la división euclidiana de por 2. no es necesariamente un número entero.${\displaystyle H^{\prime }\;{\bmod {2}}}$${\displaystyle H^{\prime}}$${\displaystyle H^{\prime}}$

${\displaystyle (R_{1},G_{1},B_{1})={\begin{cases}(C,X,0)&{\text{si }}0\leq H^{\prime }<1\\(X,C,0)&{\text{si }}1\leq H^{\prime }<2\\(0,C,X)&{\text{si }}2\leq H^{\prime }<3\\(0,X,C)&{\text{si }}3\leq H^{\prime }<4\\(X,0,C)&{\text{si }}4\leq H^{\prime }<5\\(C,0,X)&{\text{si }}5\leq H^{\prime }<6\end{cases}}}$

Cuando es un número entero, la fórmula "vecina" arrojaría el mismo resultado, como o , según corresponda.${\displaystyle H^{\prime}}$${\estilo de visualización X=0}$${\displaystyle X=C}$

Finalmente, podemos encontrar R , G y B agregando la misma cantidad a cada componente, para que coincida con la luminosidad:

${\displaystyle m=L-{\frac {C}{2}}}$

${\displaystyle (R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)}$

Las funciones poligonales por partes se pueden simplificar un poco mediante un uso inteligente de los valores mínimos y máximos, así como de la operación restante.

Dado un color con tono , saturación y luminosidad , primero definimos la función:${\displaystyle H\in [0^{\circ },360^{\circ }]}$${\displaystyle S=S_{L}\en [0,1]}$${\displaystyle L\in [0,1]}$

${\displaystyle f(n)=La\max(-1,\min(k-3,9-k,1))}$

donde y:${\displaystyle k,n\in \mathbb {R} _{\geq 0}}$

${\displaystyle k=(n+{\frac {H}{30^{\circ }}}){\bmod {1}}2}$

${\displaystyle a=S_{L}\min(L,1-L)}$

Y los valores de salida R,G,B (de ) son:${\displaystyle [0,1]^{3}}$

${\displaystyle (R,G,B)=(f(0),f(8),f(4))}$

Las fórmulas alternativas anteriores permiten implementaciones más cortas. En las fórmulas anteriores, la operación también devuelve la parte fraccionaria del módulo, por ejemplo , y . ${\displaystyle a{\bmod {b}}}$${\displaystyle 7.4{\bmod {6}}=1.4}$${\displaystyle k\in [0,12)}$

La forma base se construye de la siguiente manera: es un "triángulo" para el cual los valores mayores o iguales a −1 comienzan en k=2 y terminan en k=10, y el punto más alto está en k=6. Luego con cambiamos los valores mayores que 1 para que sean iguales a 1. Luego con cambiamos los valores menores que −1 para que sean iguales a −1. En este punto, obtenemos algo similar a la forma roja de la fig. 24 después de un giro vertical (donde el máximo es 1 y el mínimo es −1). Las funciones R,G,B de usan esta forma transformada de la siguiente manera: módulo desplazado en (por ) (de manera diferente para R,G,B) escalado en (por ) y desplazado en (por ). ${\displaystyle T(k)=t(n,H)=\max(\min(k-3,9-k,1),-1)}$${\displaystyle t_{1}=\min(k-3,9-k)}$${\displaystyle t_{2}=\min(t_{1},1)=\min(k-3,9-k,1)}$${\displaystyle t=\max(t_{2},-1)}$${\displaystyle H}$${\displaystyle X}$${\displaystyle n}$${\displaystyle Y}$${\displaystyle -a}$${\displaystyle Y}$${\displaystyle L}$

Observamos las siguientes propiedades de forma (la figura 24 puede ayudar a tener una idea sobre ellas):

${\displaystyle t(n,H)=-t(n+6,H)}$

${\displaystyle \min \ (t(n,H),t(n+4,H),t(n+8,H))=-1}$

${\displaystyle \max \ (t(n,H),t(n+4,H),t(n+8,H))=+1}$

Dado un color HSV con tono H ∈ [0°, 360°) , saturación S _V ∈ [0, 1] y valor V ∈ [0, 1] , podemos utilizar la misma estrategia. Primero, encontramos el croma:

${\displaystyle C=V\times S_{V}}$

Luego podemos, nuevamente, encontrar un punto ( R ₁ , G ₁ , B ₁ ) a lo largo de las tres caras inferiores del cubo RGB, con el mismo tono y croma que nuestro color (usando el valor intermedio X para el segundo componente más grande de este color):

${\displaystyle H^{\prime }={\frac {H}{60^{\circ }}}}$

${\displaystyle X=C\times (1-|H^{\prime }{\bmod {2}}-1|)}$

${\displaystyle (R_{1},G_{1},B_{1})={\begin{cases}(C,X,0)&{\text{if }}0\leq H^{\prime }<1\\(X,C,0)&{\text{if }}1\leq H^{\prime }<2\\(0,C,X)&{\text{if }}2\leq H^{\prime }<3\\(0,X,C)&{\text{if }}3\leq H^{\prime }<4\\(X,0,C)&{\text{if }}4\leq H^{\prime }<5\\(C,0,X)&{\text{if }}5\leq H^{\prime }<6\end{cases}}}$

Como antes, cuando es un número entero, las fórmulas "vecinas" producirían el mismo resultado.${\displaystyle H^{\prime }}$

Finalmente, podemos encontrar R , G y B sumando la misma cantidad a cada componente, para que coincida con el valor:

${\displaystyle m=V-C}$

${\displaystyle (R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)}$

Dado un color con tono , saturación y valor , primero definimos la función:${\displaystyle H\in [0^{\circ },360^{\circ }]}$${\displaystyle S=S_{V}\in [0,1]}$${\displaystyle V\in [0,1]}$

${\displaystyle f(n)=V-VS\max(0,\min(k,4-k,1))}$

donde y:${\displaystyle k,n\in \mathbb {R} _{\geq 0}}$

${\displaystyle k=(n+{\frac {H}{60^{\circ }}}){\bmod {6}}}$

Y los valores de salida R,G,B (de ) son:${\displaystyle [0,1]^{3}}$

${\displaystyle (R,G,B)=(f(5),f(3),f(1))}$

Las fórmulas alternativas equivalentes anteriores permiten una implementación más corta. En las fórmulas anteriores, también se devuelve la parte fraccionaria del módulo, por ejemplo, la fórmula . Los valores de . La forma base${\displaystyle a{\bmod {b}}}$${\displaystyle 7.4{\bmod {6}}=1.4}$${\displaystyle k\in \mathbb {R} \land k\in [0,6)}$

${\displaystyle t(n,H)=T(k)=\max(0,\min(k,4-k,1))}$

se construye de la siguiente manera: es un "triángulo" para el cual los valores no negativos comienzan en k=0, el punto más alto en k=2 y "terminan" en k=4, luego cambiamos los valores mayores que uno a uno por , luego cambiamos los valores negativos a cero por – y obtenemos (para ) algo similar a la forma verde de la Fig. 24 (cuyo valor máximo es 1 y el valor mínimo es 0). Las funciones R,G,B de usan esta forma transformada de la siguiente manera: módulo desplazado en (por ) (de manera diferente para R,G,B) escalado en (por ) y desplazado en (por ). Observamos las siguientes propiedades de forma (la Fig. 24 puede ayudar a tener una intuición sobre esto):${\displaystyle t_{1}=\min(k,4-k)}$${\displaystyle t_{2}=\min(t_{1},1)=\min(k,4-k,1)}$${\displaystyle t=\max(t2,0)}$${\displaystyle n=0}$${\displaystyle H}$${\displaystyle X}$${\displaystyle n}$${\displaystyle Y}$${\displaystyle -VS}$${\displaystyle Y}$${\displaystyle V}$

${\displaystyle t(n,H)=1-t(n+3,H)}$

${\displaystyle \min(t(n,H),t(n+2,H),t(n+4,H))=0}$

${\displaystyle \max(t(n,H),t(n+2,H),t(n+4,H))=1}$

Dado un color HSI con tono H ∈ [0°, 360°) , saturación S _I ∈ [0, 1] e intensidad I ∈ [0, 1] , podemos utilizar la misma estrategia, en un orden ligeramente diferente:

${\displaystyle H^{\prime }={\frac {H}{60^{\circ }}}}$

${\displaystyle Z=1-|H^{\prime }\;{\bmod {2}}-1|}$

${\displaystyle C={\frac {3\cdot I\cdot S_{I}}{1+Z}}}$

${\displaystyle X=C\cdot Z}$

¿Dónde está el croma?${\displaystyle C}$

Luego podemos, nuevamente, encontrar un punto ( R ₁ , G ₁ , B ₁ ) a lo largo de las tres caras inferiores del cubo RGB, con el mismo tono y croma que nuestro color (usando el valor intermedio X para el segundo componente más grande de este color):

${\displaystyle (R_{1},G_{1},B_{1})={\begin{cases}(0,0,0)&{\text{if }}H{\text{ is undefined}}\\(C,X,0)&{\text{if }}0\leq H^{\prime }\leq 1\\(X,C,0)&{\text{if }}1\leq H^{\prime }\leq 2\\(0,C,X)&{\text{if }}2\leq H^{\prime }\leq 3\\(0,X,C)&{\text{if }}3\leq H^{\prime }\leq 4\\(X,0,C)&{\text{if }}4\leq H^{\prime }\leq 5\\(C,0,X)&{\text{if }}5\leq H^{\prime }<6\end{cases}}}$

La superposición (cuando es un número entero) se produce porque dos formas de calcular el valor son equivalentes: o , según corresponda.${\displaystyle H^{\prime }}$${\displaystyle X=0}$${\displaystyle X=C}$

Finalmente, podemos encontrar R , G y B agregando la misma cantidad a cada componente, para que coincida con la luminosidad:

${\displaystyle m=I\cdot (1-S_{I})}$

${\displaystyle (R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)}$

Dado un color con tono H ∈ [0°, 360°) , croma C ∈ [0, 1] y luma Y ′ ₆₀₁ ∈ [0, 1] , ^[U] podemos volver a utilizar la misma estrategia. Como ya tenemos H y C , podemos encontrar directamente nuestro punto ( R ₁ , G ₁ , B ₁ ) a lo largo de las tres caras inferiores del cubo RGB:

${\displaystyle {\begin{aligned}H^{\prime }&={\frac {H}{60^{\circ }}}\\X&=C\times (1-|H^{\prime }{\bmod {2}}-1|)\end{aligned}}}$

${\displaystyle (R_{1},G_{1},B_{1})={\begin{cases}(0,0,0)&{\text{if }}H{\text{ is undefined}}\\(C,X,0)&{\text{if }}0\leq H^{\prime }\leq 1\\(X,C,0)&{\text{if }}1\leq H^{\prime }\leq 2\\(0,C,X)&{\text{if }}2\leq H^{\prime }\leq 3\\(0,X,C)&{\text{if }}3\leq H^{\prime }\leq 4\\(X,0,C)&{\text{if }}4\leq H^{\prime }\leq 5\\(C,0,X)&{\text{if }}5\leq H^{\prime }<6\end{cases}}}$

La superposición (cuando es un número entero) se produce porque dos formas de calcular el valor son equivalentes: o , según corresponda.${\displaystyle H^{\prime }}$${\displaystyle X=0}$${\displaystyle X=C}$

Luego podemos encontrar R , G y B agregando la misma cantidad a cada componente, para que coincida con la luminancia:

${\displaystyle m=Y_{601}^{\prime }-(0.30R_{1}+0.59G_{1}+0.11B_{1})}$

${\displaystyle (R,G,B)=(R_{1}+m,G_{1}+m,B_{1}+m)}$

Dado un color con tono , saturación y valor ,${\displaystyle H_{V}\in [0^{\circ },360^{\circ })}$${\displaystyle S_{V}\in [0,1]}$${\displaystyle V\in [0,1]}$

${\displaystyle H_{L}=H_{V}}$

${\displaystyle S_{L}={\begin{cases}0&{\text{if }}L=0{\text{ or }}L=1\\{\frac {V-L}{\min(L,1-L)}}&{\text{otherwise}}\\\end{cases}}}$

${\displaystyle L=V\left(1-{\frac {S_{V}}{2}}\right)}$

Dado un color con tono , saturación y luminancia ,${\displaystyle H_{L}\in [0^{\circ },360^{\circ })}$${\displaystyle S_{L}\in [0,1]}$${\displaystyle L\in [0,1]}$

${\displaystyle H_{V}=H_{L}}$

${\displaystyle S_{V}={\begin{cases}0&{\text{if }}V=0\\2\left(1-{\frac {L}{V}}\right)&{\text{otherwise}}\\\end{cases}}}$

${\displaystyle V=L+S_{L}\min(L,1-L)}$

Esta es una reiteración de la conversión anterior.

El valor debe estar dentro del rango .${\displaystyle R,G,B\in [0,1]}$

Con el componente máximo (es decir, el valor)

${\displaystyle X_{\text{max}}:=\max(R,G,B)=:V}$

y componente mínimo

${\displaystyle X_{\text{min}}:=\min(R,G,B)=V-C}$,

rango (es decir, croma)

${\displaystyle C:=X_{\text{max}}-X_{\text{min}}=2(V-L)}$

y gama media (es decir, ligereza)

${\displaystyle L:=\operatorname {mid} (R,G,B)={\frac {X_{\text{max}}+X_{\text{min}}}{2}}=V-{\frac {C}{2}}}$,

obtenemos un tono común:

${\displaystyle H:={\begin{cases}0,&{\text{if }}C=0\\60^{\circ }\cdot \left({\frac {G-B}{C}}\mod 6\right),&{\text{if }}V=R\\60^{\circ }\cdot \left({\frac {B-R}{C}}+2\right),&{\text{if }}V=G\\60^{\circ }\cdot \left({\frac {R-G}{C}}+4\right),&{\text{if }}V=B\end{cases}}}$

y saturaciones distintas:

${\displaystyle S_{V}:={\begin{cases}0,&{\text{if }}V=0\\{\frac {C}{V}},&{\text{otherwise}}\end{cases}}}$

${\displaystyle S_{L}:={\begin{cases}0,&{\text{if }}L=0{\text{ or }}L=1\\{\frac {C}{1-\left\vert 2V-C-1\right\vert }}={\frac {2(V-L)}{1-\left\vert 2L-1\right\vert }}={\frac {V-L}{\min(L,1-L)}},&{\text{otherwise}}\end{cases}}}$

Pase el cursor sobre las muestras a continuación para ver los valores R , G y B de cada muestra en una información sobre herramientas .

• Sistema de color Munsell
• Espacio de color TSL