Desorden (radar)

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Clutter" radar – news · newspapers · books · scholar · JSTOR (December 2016) (Learn how and when to remove this message)

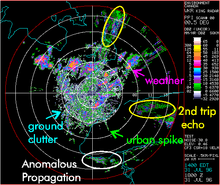
El eco no deseado ^{[1] [2]} es el eco no deseado que se emite en los sistemas electrónicos, en particular en los radares . Dichos ecos suelen provenir del suelo , el mar, la lluvia, los animales o insectos, la paja y las turbulencias atmosféricas , y pueden provocar graves problemas de rendimiento en los sistemas de radar. Lo que una persona considera eco no deseado, otra puede considerarlo un objetivo deseado. Sin embargo, los objetivos suelen referirse a los dispersores puntuales y el eco a los dispersores extendidos (que abarcan muchas celdas de rango, ángulo y Doppler). El eco puede llenar un volumen (como la lluvia) o limitarse a una superficie (como la tierra). Se requiere conocer el volumen o la superficie iluminada para estimar el eco por unidad de volumen, η, o el eco por unidad de superficie, σ° (el coeficiente de retrodispersión del radar ).

El desorden puede ser causado por objetos artificiales como edificios y, intencionalmente, por contramedidas de radar como paja . Otras causas incluyen objetos naturales como características del terreno, mar, precipitación , picos de granizo , tormentas de polvo , pájaros, turbulencia en la circulación atmosférica y rastros de meteoritos . El desorden del radar también puede ser causado por otros fenómenos atmosféricos, como perturbaciones en la ionosfera causadas por tormentas geomagnéticas u otros eventos meteorológicos espaciales . Este fenómeno es especialmente evidente cerca de los polos geomagnéticos , donde la acción del viento solar en la magnetosfera de la Tierra produce patrones de convección en el plasma ionosférico . ^[3] El desorden del radar puede degradar la capacidad del radar sobre el horizonte para detectar objetivos. ^{[3] [4]} El desorden también puede originarse a partir de ecos de trayectos múltiples de objetivos válidos causados ​​por la reflexión del suelo , la canalización atmosférica o la reflexión / refracción ionosférica (por ejemplo, propagación anómala ). Este tipo de desorden es especialmente molesto ya que parece moverse y comportarse como objetivos de interés comunes, como aviones o globos meteorológicos .

Las señales electromagnéticas procesadas por un receptor de radar constan de tres componentes principales: señal útil (por ejemplo, ecos de aeronaves), interferencias y ruido . La señal total que compite con la señal de retorno del objetivo es, por lo tanto, interferencia más ruido. ^[5] En la práctica, a menudo no hay interferencias o predominan y el ruido se puede ignorar. En el primer caso, se dice que el radar está limitado por el ruido, mientras que en el segundo está limitado por las interferencias.

La lluvia, el granizo, la nieve y la paja son ejemplos de ruido de volumen. Por ejemplo, supongamos que un objetivo en el aire, a una distancia de , se encuentra dentro de una tormenta de lluvia. ¿Cuál es el efecto sobre la detectabilidad del objetivo?${\displaystyle R}$

Primero, encuentre la magnitud del retorno del eco. Suponga que el eco llena la celda que contiene el objetivo, que los dispersores son estadísticamente independientes y que los dispersores están distribuidos uniformemente a través del volumen. El volumen del eco iluminado por un pulso se puede calcular a partir de los anchos del haz y la duración del pulso, Figura 1. Si c es la velocidad de la luz y es la duración del pulso transmitido, entonces el pulso que regresa de un objetivo es equivalente a una extensión física de c , al igual que el retorno de cualquier elemento individual del eco. Los anchos del haz de acimut y elevación, en un rango , son y respectivamente si se supone que la celda iluminada tiene una sección transversal elíptica.${\displaystyle \tau }$${\displaystyle \tau }$${\displaystyle R}$${\displaystyle \theta /2}$${\displaystyle \phi /2}$

El volumen de la celda iluminada es entonces:

${\displaystyle \ V_{m}=\pi R\tan(\theta /2)R\tan(\phi /2)(c\tau /2)}$

Para ángulos pequeños esto se simplifica a:

${\displaystyle \ V_{m}\approx {\frac {\pi }{4}}(R\theta )(R\phi )(c\tau /2)}$

Se supone que el ruido es una gran cantidad de dispersores independientes que llenan la celda que contiene el objetivo de manera uniforme. El retorno del ruido del volumen se calcula como para la ecuación de radar normal , pero la sección transversal del radar se reemplaza por el producto del coeficiente de retrodispersión de volumen, , y el volumen de la celda del ruido, como se derivó anteriormente. El retorno del ruido es entonces${\displaystyle \eta }$

${\displaystyle \ C={\frac {P_{t}G_{t}A_{r}}{(4\pi )^{2}R^{4}}}{\frac {\pi }{4}}(R\theta )(R\phi )(c\tau /2)\eta }$

dónde

• ${\displaystyle P_{t}}$= potencia del transmisor (vatios)
• ${\displaystyle G_{t}}$= ganancia de la antena transmisora
• ${\displaystyle A_{r}}$= apertura efectiva (área) de la antena receptora
• ${\displaystyle R}$= distancia del radar al objetivo

Se debe realizar una corrección para tener en cuenta el hecho de que la iluminación del eco no es uniforme en todo el ancho del haz. En la práctica, la forma del haz se aproximará a una función sinc que a su vez se aproxima a una función gaussiana . El factor de corrección se obtiene integrando en todo el ancho del haz la aproximación gaussiana de la antena. La potencia retrodispersada corregida es

${\displaystyle \ C={\frac {P_{t}G_{t}A_{r}}{2\log 2(4\pi )^{2}R^{4}}}{\frac {\pi }{4}}(R\theta )(R\phi )(c\tau /2)\eta }$

Se pueden realizar varias sustituciones simplificadoras. La apertura de la antena receptora está relacionada con su ganancia mediante:

${\displaystyle \ A_{r}={\frac {G\lambda ^{2}}{4\pi }}}$

y la ganancia de la antena está relacionada con los dos anchos de haz mediante:

${\displaystyle \ G={\frac {\pi ^{2}}{\theta \phi }}}$

Generalmente se utiliza la misma antena tanto para transmisión como para recepción, por lo que la potencia de interferencia recibida es:

${\displaystyle \ C={\frac {P_{t}G\lambda ^{2}}{1024(\log 2)R^{2}}}c\tau \eta }$

Si la potencia de retorno de ruido es mayor que la potencia de ruido del sistema, entonces el radar está limitado por el ruido y la relación señal/ruido debe ser igual o mayor que la relación señal/ruido mínima para que el objetivo sea detectable.

De la ecuación del radar, el retorno desde el propio objetivo será

${\displaystyle \ S={\frac {P_{t}G^{2}\lambda ^{2}}{(4\pi )^{3}R^{4}}}\sigma }$

con una expresión resultante para la relación señal/desorden de

${\displaystyle \ {\frac {S}{C}}={\frac {1024(\log 2)G\sigma }{(4\pi )^{3}R^{2}c\tau \eta }}}$

La implicación es que cuando el radar está limitado por el ruido, la variación de la relación señal/ruido es una cuarta potencia inversa. Reducir a la mitad la distancia hará que la relación señal/ruido aumente (mejore) en un factor de 16. Sin embargo, cuando el radar está limitado por el ruido de volumen, la variación es una ley del cuadrado inverso y reducir a la mitad la distancia hará que la relación señal/ruido mejore solo cuatro veces.

Desde

${\displaystyle \ G={\frac {\pi ^{2}}{\theta \phi }}}$

resulta que

${\displaystyle \ {\frac {S}{C}}={\frac {16(\log 2)\sigma }{\pi R^{2}\theta \phi c\tau \eta }}}$

Es evidente que se necesitan anchos de haz estrechos y pulsos cortos para reducir el efecto del eco mediante la reducción del volumen de la celda de eco. Si se utiliza compresión de pulsos , la duración de pulso adecuada que se debe utilizar en el cálculo es la del pulso comprimido, no la del pulso transmitido.

Un problema con el ruido de volumen, por ejemplo la lluvia, es que el volumen iluminado puede no estar completamente lleno, en cuyo caso se debe conocer la fracción llena, y los dispersores pueden no estar distribuidos uniformemente. Consideremos un haz de 10° de elevación. A un alcance de 10 km, el haz podría cubrir desde el nivel del suelo hasta una altura de 1750 metros. Podría haber lluvia al nivel del suelo, pero la parte superior del haz podría estar por encima del nivel de las nubes. En la parte del haz que contiene lluvia, la tasa de lluvia no será constante. Sería necesario saber cómo se distribuyó la lluvia para hacer una evaluación precisa del ruido y la relación señal/ruido. Todo lo que se puede esperar de la ecuación es una estimación a los 5 o 10 dB más cercanos.

El eco de la superficie depende de la naturaleza de la misma, su rugosidad, el ángulo rasante (ángulo que forma el haz con la superficie), la frecuencia y la polarización. La señal reflejada es la suma fasorial de un gran número de ecos individuales de distintas fuentes, algunas de ellas capaces de moverse (hojas, gotas de lluvia, ondulaciones) y otras estacionarias (torres, edificios, troncos de árboles). Las muestras individuales de eco varían de una celda de resolución a otra (variación espacial) y varían con el tiempo para una celda determinada (variación temporal).

En el caso de un objetivo cercano a la superficie de la Tierra, de modo que la Tierra y el objetivo se encuentren en la misma celda de resolución, se pueden dar dos situaciones. El caso más común es cuando el haz intersecta la superficie en un ángulo tal que el área iluminada en un momento dado es solo una fracción de la superficie intersectada por el haz, como se ilustra en la Figura 2.

En el caso de longitud de pulso limitada, el área iluminada depende del ancho de acimut del haz y de la longitud del pulso, medido a lo largo de la superficie. El parche iluminado tiene un ancho en acimut de

${\displaystyle \ 2R\tan \theta /2}$.

La longitud medida a lo largo de la superficie es

${\displaystyle \ (c\tau /2)\sec \psi }$.

El área iluminada por el radar viene dada por

${\displaystyle \ A=2R(c\tau /2)(\tan \theta /2)\sec \psi }$

Para anchos de haz 'pequeños' esto se aproxima a

${\displaystyle \ A=R(c\tau /2)\theta \sec \psi }$

El retorno del desorden es entonces

${\displaystyle \ C={\frac {P_{t}G^{2}\lambda ^{2}}{(4\pi )^{3}R^{4}}}A\sigma ^{o}}$ Vatios

Sustituyendo el área iluminada${\displaystyle A}$

${\displaystyle \ C={\frac {c}{2^{7}\pi ^{3}}}{\frac {P_{t}G^{2}\lambda ^{2}}{R^{3}}}\tau \theta \sec \psi \sigma ^{o}}$ Vatios

donde es el coeficiente de retrodispersión del ruido. Al convertir a grados e introducir los valores numéricos se obtiene${\displaystyle \sigma ^{o}}$${\displaystyle \theta }$

${\displaystyle \ C=1300{\frac {P_{t}G^{2}\lambda ^{2}}{R^{3}}}\tau \theta ^{o}\sec \psi \sigma ^{o}}$ Vatios

La expresión para el retorno objetivo permanece sin cambios, por lo tanto, la relación señal/suciedad es

${\displaystyle \ {\frac {S}{C}}={\frac {1}{1300}}{\frac {R^{3}}{P_{t}G^{2}\lambda ^{2}}}{\frac {1}{\tau \theta \sec \psi \sigma ^{o}}}{\frac {P_{t}G^{2}\lambda ^{2}}{(4\pi )^{3}R^{4}}}\sigma }$ Vatios

Esto se simplifica a

${\displaystyle \ {\frac {S}{C}}=4\times 10^{-7}{\frac {\cos \psi }{R\tau \theta }}{\frac {\sigma }{\sigma ^{o}}}}$

En el caso del ruido de superficie, la relación señal/ruido ahora varía inversamente con R. Reducir a la mitad la distancia solo provoca una duplicación de la relación (una mejora de un factor de dos).

Existen varios problemas a la hora de calcular la relación señal/interferencia. La interferencia en el haz principal se extiende a lo largo de un rango de ángulos rasantes y el coeficiente de retrodispersión depende del ángulo rasante. La interferencia aparecerá en los lóbulos laterales de la antena, lo que a su vez implicará un rango de ángulos rasantes e incluso puede implicar interferencia de una naturaleza diferente.

El cálculo es similar a los ejemplos anteriores, en este caso el área iluminada es

${\displaystyle \ A=\pi R^{2}\tan ^{2}\theta /2}$

Lo cual para anchos de haz pequeños se simplifica a

${\displaystyle \ A\approx \pi R^{2}\theta ^{2}/4}$

El retorno del desorden es como antes

${\displaystyle \ C={\frac {P_{t}G^{2}\lambda ^{2}}{(4\pi )^{3}R^{4}}}A\sigma ^{o}}$ Vatios

Sustituyendo el área iluminada${\displaystyle A}$

${\displaystyle \ C={\frac {P_{t}G^{2}\lambda ^{2}}{(4\pi )^{3}R^{4}}}\pi R^{2}(\theta /2)^{2}\sigma ^{o}}$ Vatios

Esto se puede simplificar así:

${\displaystyle \ C={\frac {P_{t}G^{2}\lambda ^{2}}{4^{4}\pi ^{2}R^{2}}}\theta ^{2}\sigma ^{o}}$ Vatios

Convirtiendo a grados${\displaystyle \theta }$

${\displaystyle \ C={\frac {P_{t}G^{2}\lambda ^{2}}{4^{4}R^{2}}}(\theta ^{o}/180)^{2}\sigma ^{o}}$ Vatios

El objetivo de retorno permanece sin cambios, por lo tanto

${\displaystyle \ {\frac {S}{C}}={\frac {4^{4}R^{2}}{P_{t}G^{2}\lambda ^{2}}}(180/\theta ^{o})^{2}{\frac {1}{\sigma ^{o}}}{\frac {P_{t}G^{2}\lambda ^{2}}{(4\pi )^{3}R^{4}}}\sigma }$

Lo cual se simplifica a

${\displaystyle \ {\frac {S}{C}}=5.25\times 10^{4}{\frac {1}{\theta ^{o2}R^{2}}}{\frac {\sigma }{\sigma ^{o}}}}$

Al igual que en el caso del ruido de volumen, la relación señal/ruido sigue una ley del cuadrado inverso.

El problema general más importante es que, en general, el coeficiente de retrodispersión no se puede calcular y debe medirse. El problema es la validez de las mediciones tomadas en un lugar bajo un conjunto de condiciones que se utilizan para un lugar diferente bajo condiciones diferentes. Existen varias fórmulas y gráficos empíricos que permiten realizar una estimación, pero los resultados deben utilizarse con cautela.

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (January 2024) (Learn how and when to remove this message)

El término "pliegue de interferencias " se utiliza para describir el "desorden" detectado por los sistemas de radar . El plegamiento de interferencias se convierte en un problema cuando el alcance de la interferencia (detectada por el radar) excede el intervalo de frecuencia de repetición de pulsos del radar, y ya no proporciona una supresión de interferencias adecuada, y la interferencia se "pliega" de nuevo dentro del alcance. ^[6] La solución a este problema suele ser añadir pulsos de relleno a cada intervalo de tiempo coherente del radar, aumentando el alcance en el que el sistema aplica la supresión de interferencias.

La desventaja de hacer esto es que agregar pulsos de relleno degradará el rendimiento, debido al desperdicio de energía del transmisor y a un tiempo de permanencia más largo .