Sistema de Lorenz

Este artículo puede resultar demasiado técnico para que la mayoría de los lectores lo comprendan . Ayúdenos a mejorarlo para que sea comprensible para los no expertos , sin eliminar los detalles técnicos. ( Diciembre de 2023 ) ( Aprenda cómo y cuándo eliminar este mensaje )

El sistema de Lorenz es un sistema de ecuaciones diferenciales ordinarias estudiado por primera vez por el matemático y meteorólogo Edward Lorenz . Es notable por tener soluciones caóticas para ciertos valores de parámetros y condiciones iniciales. En particular, el atractor de Lorenz es un conjunto de soluciones caóticas del sistema de Lorenz. El término " efecto mariposa " en los medios populares puede provenir de las implicaciones del mundo real del atractor de Lorenz, es decir, que pequeños cambios en las condiciones iniciales evolucionan a trayectorias completamente diferentes. Esto subraya que los sistemas caóticos pueden ser completamente deterministas y, sin embargo, ser inherentemente imprácticos o incluso imposibles de predecir durante períodos de tiempo más largos. Por ejemplo, incluso el pequeño aleteo de las alas de una mariposa podría hacer que la atmósfera de la Tierra siga una trayectoria muy diferente, en la que, por ejemplo, se produce un huracán donde de otra manera no se habría producido (ver Puntos de silla ). La forma del propio atractor de Lorenz, cuando se representa gráficamente en el espacio de fases , también puede parecerse a una mariposa.

En 1963, Edward Lorenz , con la ayuda de Ellen Fetter , quien fue responsable de las simulaciones numéricas y las figuras, ^[1] y Margaret Hamilton, quien ayudó en los cálculos numéricos iniciales que condujeron a los hallazgos del modelo de Lorenz, ^[2] desarrolló un modelo matemático simplificado para la convección atmosférica . ^[1] El modelo es un sistema de tres ecuaciones diferenciales ordinarias ahora conocidas como ecuaciones de Lorenz:

${\displaystyle {\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma (yx),\\[6pt]{\frac {\mathrm {d} y}{\mathrm {d} t}}&=x(\rho -z)-y,\\[6pt]{\frac {\mathrm {d} z}{\mathrm {d} t}}&=xy-\beta z.\end{aligned}}}$

Las ecuaciones relacionan las propiedades de una capa de fluido bidimensional calentada uniformemente desde abajo y enfriada desde arriba. En particular, las ecuaciones describen la tasa de cambio de tres cantidades con respecto al tiempo: x es proporcional a la tasa de convección, y a la variación horizontal de la temperatura y z a la variación vertical de la temperatura. ^[3] Las constantes σ , ρ y β son parámetros del sistema proporcionales al número de Prandtl , al número de Rayleigh y a ciertas dimensiones físicas de la propia capa. ^[3]

Las ecuaciones de Lorenz pueden surgir en modelos simplificados para láseres , ^[4] dinamos , ^[5] termosifones , ^[6] motores de CC sin escobillas , ^[7] circuitos eléctricos , ^[8] reacciones químicas, ^[9] y ósmosis directa . ^[10] Las ecuaciones de Lorenz también son las ecuaciones que gobiernan en el espacio de Fourier la rueda hidráulica de Malkus . ^{[11] [12]} La rueda hidráulica de Malkus exhibe un movimiento caótico donde en lugar de girar en una dirección a una velocidad constante, su rotación se acelerará, desacelerará, se detendrá, cambiará de dirección y oscilará de un lado a otro entre combinaciones de tales comportamientos de manera impredecible.

Desde un punto de vista técnico, el sistema de Lorenz es no lineal , aperiódico, tridimensional y determinista . Las ecuaciones de Lorenz han sido objeto de cientos de artículos de investigación y al menos un estudio extenso. ^[3]

Normalmente se supone que los parámetros σ , ρ y β son positivos. Lorenz utilizó los valores σ = 10 , β = ⁠8/3⁠ y ρ = 28. El sistema exhibe un comportamiento caótico para estos valores (y otros cercanos). ^[13]

Si ρ < 1 entonces sólo hay un punto de equilibrio, que está en el origen. Este punto corresponde a la ausencia de convección. Todas las órbitas convergen al origen, que es un atractor global , cuando ρ < 1. [ ^14]

Se produce una bifurcación en horquilla en ρ = 1 y, para ρ > 1, aparecen dos puntos críticos adicionales en Estos corresponden a una convección constante. Este par de puntos de equilibrio es estable solo si $${\displaystyle \left({\sqrt {\beta (\rho -1)}},{\sqrt {\beta (\rho -1)}},\rho -1\right)\quad {\text{y}}\quad \left(-{\sqrt {\beta (\rho -1)}},-{\sqrt {\beta (\rho -1)}},\rho -1\right).}$$

${\displaystyle \rho <\sigma {\frac {\sigma +\beta +3}{\sigma -\beta -1}},}$

que sólo puede cumplirse para ρ positivo si σ > β + 1. En el valor crítico, ambos puntos de equilibrio pierden estabilidad a través de una bifurcación de Hopf subcrítica . ^[15]

Cuando ρ  = 28 , σ  = 10 y β  =  ⁠8/3⁠ , el sistema de Lorenz tiene soluciones caóticas (pero no todas las soluciones son caóticas). Casi todos los puntos iniciales tenderán a un conjunto invariante – el atractor de Lorenz – un atractor extraño , un fractal y un atractor autoexcitado con respecto a los tres equilibrios. Su dimensión de Hausdorff se estima a partir de arriba mediante la dimensión de Lyapunov (dimensión de Kaplan-Yorke) como2,06 ± 0,01 , ^[16] y se estima que la dimensión de correlación es2,05 ± 0,01 . ^[17] La ​​fórmula exacta de la dimensión de Lyapunov del atractor global se puede encontrar analíticamente bajo restricciones clásicas sobre los parámetros: ^{[18] [16] [19]}

${\displaystyle 3-{\frac {2(\sigma +\beta +1)}{\sigma +1+{\sqrt {\left(\sigma -1\right)^{2}+4\sigma \rho }}}}}$

El atractor de Lorenz es difícil de analizar, pero la acción de la ecuación diferencial sobre el atractor se describe mediante un modelo geométrico bastante simple. ^[20] La demostración de que esto es así es el decimocuarto problema de la lista de problemas de Smale . Este problema fue el primero en ser resuelto por Warwick Tucker en 2002. ^[21]

Para otros valores de ρ , el sistema muestra órbitas periódicas anudadas. Por ejemplo, con ρ = 99,96 se convierte en un nudo toroidal T (3,2) .

Ejemplos de soluciones del sistema de Lorenz para diferentes valores de ρ
ρ = 14, σ = 10, β = ⁠8/3⁠ (Ampliar)	ρ = 13, σ = 10, β = ⁠8/3⁠ (Ampliar)
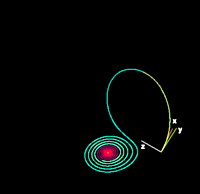ρ = 15, σ = 10, β = ⁠8/3⁠ (Ampliar)	ρ = 28, σ = 10, β = ⁠8/3⁠ (Ampliar)
Para valores pequeños de ρ , el sistema es estable y evoluciona hacia uno de dos puntos fijos atractores. Cuando ρ > 24,74 , los puntos fijos se convierten en repulsores y la trayectoria es repelida por ellos de una manera muy compleja.

Dependencia sensible de la condición inicial
Tiempo t = 1 (Ampliar)	Tiempo t = 2 (Ampliar)	Tiempo t = 3 (Ampliar)
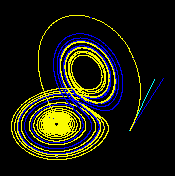Estas cifras, hechas usando ρ = 28 , σ = 10 y β = ⁠8/3⁠ — muestra tres segmentos temporales de la evolución tridimensional de dos trayectorias (una en azul, otra en amarillo) en el atractor de Lorenz, comenzando en dos puntos iniciales que difieren solo en 10 −5 en la coordenada x . Inicialmente, las dos trayectorias parecen coincidentes (solo se puede ver la amarilla, ya que está dibujada sobre la azul), pero, después de un tiempo, la divergencia es obvia.

Divergencia de trayectorias cercanas.
Evolución de tres trayectorias inicialmente cercanas del sistema de Lorenz. En esta animación, la ecuación se integra numéricamente utilizando una rutina de Runge-Kutta, realizada a partir de tres condiciones iniciales (0,9,0,0) (verde), (1,0,0,0) (azul) y (1,1,0,0) (rojo). Producida con WxMaxima .
Los parámetros son: , y . Se observa una divergencia significativa alrededor de , más allá de la cual las trayectorias dejan de estar correlacionadas. Se puede acceder al gráfico de tamaño completo aquí.${\displaystyle \rho = 28}$${\displaystyle \sigma = 10}$${\displaystyle \beta =8/3}$${\displaystyle t=24.0}$

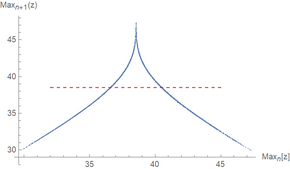
En la Figura 4 de su artículo, ^[1] Lorenz trazó el valor máximo relativo en la dirección z alcanzado por el sistema contra el máximo relativo anterior en la dirección z . Este procedimiento más tarde se conoció como un mapa de Lorenz (que no debe confundirse con un diagrama de Poincaré , que traza las intersecciones de una trayectoria con una superficie prescrita). El gráfico resultante tiene una forma muy similar al mapa de tienda . Lorenz también descubrió que cuando el valor máximo de z está por encima de un cierto límite, el sistema cambiará al siguiente lóbulo. Combinando esto con el caos que se sabe que exhibe el mapa de tienda, demostró que el sistema cambia entre los dos lóbulos de manera caótica.

En los últimos años, una serie de artículos sobre modelos de Lorenz de alta dimensión han producido un modelo de Lorenz generalizado, ^[22] que se puede simplificar en el modelo de Lorenz clásico para tres variables de estado o el siguiente modelo de Lorenz de cinco dimensiones para cinco variables de estado: ^[23]$${\displaystyle {\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma (yx),\\[6pt]{\frac {\mathrm {d} y}{\mathrm {d} t}}&=x(\rho -z)-y,\\[6pt]{\frac {\mathrm {d} z}{\mathrm {d} t}}&=xy-xy_{1}-\beta z,\\[6pt]{\frac {\mathrm {d} y_{1}}{\mathrm {d} t}}&=xz-2xz_{1}-d_{0}y_{1},\\[6pt]{\frac {\mathrm {d} z_{1}}{\mathrm {d} t}}&=2xy_{1}-4\beta z_{1}.\end{aligned}}}$$

Se ha aplicado una elección del parámetro para que sea coherente con la elección de los demás parámetros. Ver detalles en ^{[22] [23]}${\textstyle d_{0}={\dfrac {19}{3}}}$

usando gráficos # define el atractor de Lorenz @kwdef estructura mutable Lorenz dt :: Float64 = 0.02 σ :: Float64 = 10 ρ :: Float64 = 28 β :: Float64 = 8 / 3 x :: Float64 = 2 y :: Float64 = 1 z :: Float64 = 1 fin                         función paso! ( l : : Lorenz ) dx = l . σ * ( l . y - l . x ); l . x += l . dt * dx dy = l . x * ( l . ρ - l . z ) - l . y ; l . y += l . dt * dy dz = l . x * l . y - l . β * l . z ; l . z += l . dt * dz fin                                         atractor = Lorenz ()  # inicializa un gráfico 3D con 1 serie vacía plt = plot3d ( 1 , xlim = ( - 30 , 30 ), ylim = ( - 30 , 30 ), zlim = ( 0 , 60 ), title = "Lorenz Attractor" , marker = 2 , )                     # crea un gif animado empujando nuevos puntos al gráfico, guardando cada décimo cuadro @gif para i = 1 : 1500 paso ! ( atractor ) ¡ empuja ! ( plt , attractor.x , attractor.y , attractor.z ) finaliza cada 10         

deq := [ diff ( x ( t ) , t ) = 10 * ( y ( t ) - x ( t )) , diff ( y ( t ) , t ) = 28 * x ( t ) - y ( t ) - x ( t ) * z ( t ) , diff ( z ( t ) , t ) = x ( t ) * y ( t ) - 8 / 3 * z ( t )] : con ( DEtools ) : DEplot3d ( deq , { x ( t ) , y ( t ) , z ( t )} , t = 0 .. 100 , [[ x ( 0 ) = 10 , y ( 0 ) = 10 , z ( 0 ) = 10 ]] , tamaño de paso = 0,01 , x = - 20 .. 20 , y = - 25 .. 25 , z = 0 .. 50 , color de línea = sin ( t * Pi / 3 ) , grosor = 1 , orientación = [ - 40 , 80 ] , título = `Atractor caótico de Lorenz` ) ;                                                                     

[ sigma , rho , beta ] : [ 10 , 28 , 8 / 3 ]$ eq : [ sigma * ( y - x ), x * ( rho - z ) - y , x * y - beta * z ] $ sol : rk ( eq , [ x , y , z ], [ 1 , 0 , 0 ], [ t , 0 , 50 , 1/100 ] )$ len : longitud ( sol )$ x : lista de creación ( sol [ k ] [ 2 ], k , len )$ y : lista de creación ( sol [ k ][ 3 ], k , len )$ z : lista de creación ( sol [ k ][ 4 ], k , len )$ draw3d ( puntos_unidos = verdadero , tipo_punto =- 1 , puntos ( x , y , z ), ejes_proporcionales = xyz )$                                  

% Resolver sobre el intervalo de tiempo [0,100] con condiciones iniciales [1,1,1] % ''f'' es un conjunto de ecuaciones diferenciales % ''a'' es una matriz que contiene las variables x, y y z % ''t'' es una variable de tiemposigma = 10 ; beta = 8 / 3 ; rho = 28 ; f = @( t , a ) [ - sigma * a ( 1 ) + sigma * a ( 2 ); rho * a ( 1 ) - a ( 2 ) - a ( 1 ) * a ( 3 ); - beta * a ( 3 ) + a ( 1 ) * a ( 2 )]; [ t , a ] = ode45 ( f ,[ 0 100 ],[ 1 1 1 ]); % Solucionador de EDO de Runge-Kutta de 4.º/5.º orden plot3 ( a (:, 1 ), a (:, 2 ), a (:, 3 ))                         

Forma estándar:

tender = 50 ; eq = { x ' [ t ] == σ ( y [ t ] - x [ t ]), y ' [ t ] == x [ t ] ( ρ - z [ t ]) - y [ t ], z ' [ t ] == x [ t ] y [ t ] - β z [ t ]}; inicio = { x [ 0 ] == 10 , y [ 0 ] == 10 , z [ 0 ] == 10 }; pars = { σ -> 10 , ρ -> 28 , β - > 8/3 } ; { xs , ys , zs } = NDSolveValue [{ eq /. pars , init }, { x , y , z }, { t , 0 , tend }]; ParametricPlot3D [{ xs [ t ], ys [ t ], zs [ t ]}, { t , 0 , tend }]                                                           

Menos verboso:

lorenz = NonlinearStateSpaceModel [{{ σ ( y - x ), x ( ρ - z ) - y , x y - β z }, {}}, { x , y , z }, { σ , ρ , β }]; soln [ t_ ] = RespuestaEstado [{ lorenz , { 10 , 10 , 10 } } , { 10 , 28 , 8/3 } , { t , 0 , 50 }]; ParametricPlot3D [ soln [ t ], { t , 0 , 50 }]                                     

importar  matplotlib.pyplot  como  plt importar  numpy  como  npdef  lorenz ( xyz ,  * ,  s = 10 ,  r = 28 ,  b = 2.667 ): """  Parámetros  ----------  xyz : tipo matriz, forma (3,)  Punto de interés en el espacio tridimensional.  s, r, b : float  Parámetros que definen el atractor de Lorenz.  Devuelve  -------  xyz_dot : matriz, forma (3,)  Valores de las derivadas parciales del atractor de Lorenz en *xyz*.  """  x ,  y ,  z  =  xyz  x_dot  =  s * ( y  -  x )  y_dot  =  r * x  -  y  -  x * z  z_dot  =  x * y  -  b * z  return  np . array ([ x_dot ,  y_dot ,  z_dot ])dt  =  0,01 num_pasos  =  10000xyzs  =  np . empty (( num_steps  +  1 ,  3 ))  # Se necesita uno más para los valores iniciales xyzs [ 0 ]  =  ( 0. ,  1. ,  1.05 )  # Establecer valores iniciales # Recorrer el "tiempo", calculando las derivadas parciales en el punto actual # y usándolas para estimar el siguiente punto para  i  en  el rango ( num_steps ):  xyzs [ i  +  1 ]  =  xyzs [ i ]  +  lorenz ( xyzs [ i ])  *  dt# Trazar ax  =  plt . figure () . add_subplot ( proyección = '3d' )ax . plot ( * xyzs . T ,  lw = 0.6 ) ax . set_xlabel ( " Eje X" ) ax . set_ylabel ( "Eje Y" ) ax . set_zlabel ( "Eje Z" ) ax . set_title ( "Atractor de Lorenz" )plt . mostrar ()

biblioteca ( deSolve ) biblioteca ( plotly ) # parámetros prm <- list ( sigma = 10 , rho = 28 , beta = 8 / 3 ) # valores iniciales varini <- c ( X = 1 , Y = 1 , Z = 1 )                      Lorenz <- función ( t , vars , prm ) { con ( como.lista ( vars ), { dX <- prm $ sigma * ( Y - X ) dY <- X * ( prm $ rho - Z ) - Y dZ <- X * Y - prm $ beta * Z return ( lista ( c ( dX , dY , dZ ))) }) }                            veces <- seq ( desde = 0 , hasta = 100 , por = 0.01 ) # llamar al solucionador de ode out <- ode ( y = varini , veces = veces , func = Lorenz , parms = prm )                       # para asignar color a los puntos gfill <- function ( repArr , long ) { rep ( repArr , ceiling ( long / length ( repArr )))[ 1 : long ] }      dout <- as.data.frame ( salida )  dout $ color <- gfill ( arcoiris ( 10 ), nrow ( dout ))   # Producción de gráficos con Plotly: plot_ly ( data = dout , x = ~ X , y = ~ Y , z = ~ Z , tipo = 'scatter3d' , modo = 'lines' , opacidad = 1 , línea = lista ( ancho = 6 , color = ~ color , reverscale = FALSE ) )                              

Como se muestra en el artículo original de Lorenz, ^[24] el sistema de Lorenz es una versión reducida de un sistema más grande estudiado anteriormente por Barry Saltzman. ^[25] Las ecuaciones de Lorenz se derivan de la aproximación de Oberbeck-Boussinesq a las ecuaciones que describen la circulación de fluidos en una capa poco profunda de fluido, calentada uniformemente desde abajo y enfriada uniformemente desde arriba. ^[26] Esta circulación de fluidos se conoce como convección de Rayleigh-Bénard . Se supone que el fluido circula en dos dimensiones (vertical y horizontal) con condiciones de contorno rectangulares periódicas. ^[27]

Las ecuaciones diferenciales parciales que modelan la función de corriente y la temperatura del sistema se someten a una aproximación espectral de Galerkin : los campos hidrodinámicos se expanden en series de Fourier, que luego se truncan severamente a un solo término para la función de corriente y dos términos para la temperatura. Esto reduce las ecuaciones del modelo a un conjunto de tres ecuaciones diferenciales ordinarias no lineales acopladas. Se puede encontrar una derivación detallada, por ejemplo, en textos de dinámica no lineal de Hilborn (2000), Apéndice C; Bergé, Pomeau y Vidal (1984), Apéndice D; o Shen (2016), ^[28] Materiales complementarios.

La comunidad científica acepta que las características caóticas encontradas en los modelos de Lorenz de baja dimensión podrían representar características de la atmósfera de la Tierra ( ^{[29] [30] [31]} ), lo que da como resultado la afirmación de que "el clima es caótico". En comparación, basándose en el concepto de coexistencia de atractores dentro del modelo generalizado de Lorenz ^[22] y el modelo original de Lorenz ( ^{[32] [33]} ), Shen y sus coautores ^{[31] [34]} propusieron una visión revisada de que "el clima posee tanto caos como orden con una predictibilidad distintiva". La visión revisada, que es una acumulación de la visión convencional, se utiliza para sugerir que "las características caóticas y regulares encontradas en los modelos teóricos de Lorenz podrían representar mejor las características de la atmósfera de la Tierra".

El problema 14 de Smale dice: "¿Las propiedades del atractor de Lorenz exhiben las de un atractor extraño ?". El problema fue respondido afirmativamente por Warwick Tucker en 2002. ^[21] Para probar este resultado, Tucker utilizó métodos numéricos rigurosos como la aritmética de intervalos y las formas normales . Primero, Tucker definió una sección transversal que es cortada transversalmente por las trayectorias de flujo. A partir de esto, se puede definir el mapa de primer retorno , que asigna a cada uno el punto donde la trayectoria de primer se interseca .${\displaystyle \Sigma \subconjunto \{x_{3}=r-1\}}$${\estilo de visualización P}$${\displaystyle x\en \Sigma}$${\estilo de visualización P(x)}$${\estilo de visualización x}$${\estilo de visualización \Sigma}$

Luego la prueba se divide en tres puntos principales que se prueban e implican la existencia de un atractor extraño. ^[35] Los tres puntos son:

• Existe una región invariante bajo el mapa de primer retorno, es decir .${\displaystyle N\subconjunto \Sigma}$${\displaystyle P(N)\subconjunto N}$
• El mapa de retorno admite un campo de cono invariante hacia adelante.
• Los vectores dentro de este campo de cono invariante se expanden uniformemente por la derivada del mapa de retorno.${\estilo de visualización DP}$

Para probar el primer punto, notamos que la sección transversal está cortada por dos arcos formados por . ^[35] Tucker cubre la ubicación de estos dos arcos con pequeños rectángulos , la unión de estos rectángulos da . Ahora, el objetivo es probar que para todos los puntos en , el flujo traerá de vuelta los puntos en , en . Para hacer eso, tomamos un plan a continuación a una distancia pequeña, luego, tomando el centro de y usando el método de integración de Euler, uno puede estimar dónde traerá el flujo lo que nos da un nuevo punto . Luego, uno puede estimar dónde se mapearán los puntos en en usando la expansión de Taylor, esto nos da un nuevo rectángulo centrado en . Por lo tanto, sabemos que todos los puntos en se mapearán en . El objetivo es hacer este método de forma recursiva hasta que el flujo regrese a y obtengamos un rectángulo en tal que sepamos que . El problema es que nuestra estimación puede volverse imprecisa después de varias iteraciones, por lo tanto, lo que hace Tucker es dividir en rectángulos más pequeños y luego aplicar el proceso de forma recursiva. Otro problema es que a medida que aplicamos este algoritmo, el flujo se vuelve más "horizontal", ^[35] lo que genera un aumento drástico de la imprecisión. Para evitarlo, el algoritmo cambia la orientación de las secciones transversales, que pasan a ser horizontales o verticales.${\estilo de visualización \Sigma}$${\displaystyle P(\Sigma )}$${\displaystyle R_{i}}$${\estilo de visualización N}$${\estilo de visualización N}$${\estilo de visualización \Sigma}$${\estilo de visualización N}$${\displaystyle \Sigma '}$${\estilo de visualización \Sigma}$${\estilo de visualización h}$$Estilo de visualización c_{i}$${\displaystyle R_{i}}$$Estilo de visualización c_{i}$${\displaystyle \Sigma '}$$estilo de visualización c_{i}'}$${\estilo de visualización \Sigma}$${\displaystyle \Sigma '}$$Estilo de visualización R_{i}'}$$Estilo de visualización c_{i}$${\displaystyle R_{i}}$$Estilo de visualización R_{i}'}$${\estilo de visualización \Sigma}$$Estilo de visualización Rf_{i}$${\estilo de visualización \Sigma}$${\displaystyle P(R_{i})\subconjunto Rf_{i}}$$Estilo de visualización R_{i}'}$${\displaystyle R_{i,j}}$

• 
  Una solución en el atractor de Lorenz trazada en alta resolución en el plano xz .
• 
  Una solución en el atractor de Lorenz representada como SVG .
• Una animación que muestra trayectorias de múltiples soluciones en un sistema de Lorenz.
• 
  Una solución en el atractor de Lorenz representada como un cable de metal para mostrar la dirección y la estructura 3D .
• Una animación que muestra la divergencia de soluciones cercanas al sistema de Lorenz.
• 
  Una visualización del atractor de Lorenz cerca de un ciclo intermitente.
• 
  Dos líneas de corriente en un sistema de Lorenz, desde ρ = 0 hasta ρ = 28 ( σ = 10 , β = ⁠8/3⁠ ).
• 
  Animación de un sistema de Lorenz con rho-dependencia.
• 
  Animación del atractor de Lorenz en Brain Dynamics Toolbox. ^[36]

• La conjetura de Edén sobre la dimensión de Lyapunov
• Modelo Lorenz 96
• Lista de mapas caóticos
• Teorema de Takens

• Bergé, Pierre; Pomeau, Yves; Vidal, Christian (1984). Orden en el caos: hacia un enfoque determinista de la turbulencia . Nueva York: John Wiley & Sons . ISBN. 978-0-471-84967-4.
• Cuomo, Kevin M.; Oppenheim, Alan V. (1993). "Implementación de circuitos de caos sincronizado con aplicaciones a las comunicaciones". Physical Review Letters . 71 (1): 65–68. Bibcode :1993PhRvL..71...65C. doi :10.1103/PhysRevLett.71.65. ISSN  0031-9007. PMID  10054374.
• Gorman, M.; Widmann, PJ; Robbins, KA (1986). "Dinámica no lineal de un bucle de convección: una comparación cuantitativa del experimento con la teoría". Physica D . 19 (2): 255–267. Bibcode :1986PhyD...19..255G. doi :10.1016/0167-2789(86)90022-9.
• Grassberger, P.; Procaccia, I. (1983). "Medición de la extrañeza de los atractores extraños". Physica D . 9 (1–2): 189–208. Bibcode :1983PhyD....9..189G. doi :10.1016/0167-2789(83)90298-1.
• Haken, H. (1975). "Analogía entre inestabilidades superiores en fluidos y láseres". Physics Letters A . 53 (1): 77–78. Bibcode :1975PhLA...53...77H. doi :10.1016/0375-9601(75)90353-9.
• Hemati, N. (1994). "Atractores extraños en motores de corriente continua sin escobillas". IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications . 41 (1): 40–45. doi :10.1109/81.260218. ISSN  1057-7122.
• Hilborn, Robert C. (2000). Caos y dinámica no lineal: una introducción para científicos e ingenieros (segunda edición). Oxford University Press . ISBN 978-0-19-850723-9.
• Hirsch, Morris W. ; Smale, Stephen ; Devaney, Robert (2003). Ecuaciones diferenciales, sistemas dinámicos y una introducción al caos (segunda edición). Boston, MA: Academic Press . ISBN 978-0-12-349703-1.
• Knobloch, Edgar (1981). "Caos en la dinamo de disco segmentado". Physics Letters A . 82 (9): 439–440. Bibcode :1981PhLA...82..439K. doi :10.1016/0375-9601(81)90274-7.
• Kolář, Miroslav; Gumbs, Godfrey (1992). "Teoría para la observación experimental del caos en una rueda hidráulica giratoria". Physical Review A . 45 (2): 626–637. Bibcode :1992PhRvA..45..626K. doi :10.1103/PhysRevA.45.626. PMID  9907027.
• Leónov, GA; Kuznetsov, NV; Korzhemanova, NA; Kusakin, DV (2016). "Fórmula de la dimensión de Lyapunov para el atractor global del sistema de Lorenz". Comunicaciones en ciencia no lineal y simulación numérica . 41 : 84-103. arXiv : 1508.07498 . Código Bib : 2016CNSNS..41...84L. doi : 10.1016/j.cnsns.2016.04.032. S2CID  119614076.
• Lorenz, Edward Norton (1963). "Flujo no periódico determinista". Revista de Ciencias Atmosféricas . 20 (2): 130–141. Código Bibliográfico :1963JAtS...20..130L. doi : 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 .
• Mishra, Aashwin; Sanghi, Sanjeev (2006). "Un estudio de la rueda hidráulica asimétrica de Malkus: las ecuaciones de Lorenz sesgadas". Chaos: An Interdisciplinary Journal of Nonlinear Science . 16 (1): 013114. Bibcode :2006Chaos..16a3114M. doi :10.1063/1.2154792. PMID  16599745.
• Pchelintsev, AN (2014). "Modelado numérico y físico de la dinámica del sistema de Lorenz". Análisis numérico y aplicaciones . 7 (2): 159–167. doi :10.1134/S1995423914020098. S2CID  123023929.
• Polonia, Douglas (1993). "Catálisis cooperativa y caos químico: un modelo químico para las ecuaciones de Lorenz". Physica D . 65 (1): 86–99. Bibcode :1993PhyD...65...86P. doi :10.1016/0167-2789(93)90006-M.
• Saltzman, Barry (1962). "Convección libre de amplitud finita como un problema de valor inicial—I". Revista de Ciencias Atmosféricas . 19 (4): 329–341. Bibcode :1962JAtS...19..329S. doi : 10.1175/1520-0469(1962)019<0329:FAFCAA>2.0.CO;2 .
• Shen, B.-W. (21 de diciembre de 2015). "Retroalimentación no lineal en un modelo de Lorenz de seis dimensiones: impacto de un término de calentamiento adicional". Procesos no lineales en geofísica . 22 (6): 749–764. doi :10.5194/npg-22-749-2015. ISSN 1607-7946.
• Sparrow, Colin (1982). Las ecuaciones de Lorenz: bifurcaciones, caos y atractores extraños . Springer.
• Tucker, Warwick (2002). "Un solucionador riguroso de ecuaciones diferenciales ordinarias y el decimocuarto problema de Smale" (PDF) . Fundamentos de las matemáticas computacionales . 2 (1): 53–117. CiteSeerX  10.1.1.545.3996 . doi :10.1007/s002080010018. S2CID  353254.
• Tzenov, Stephan (2014). "Atractores extraños que caracterizan la inestabilidad osmótica". arXiv : 1406.0979v1 [physics.flu-dyn].
• Viana, Marcelo (2000). "¿Qué hay de nuevo en los atractores extraños de Lorenz?". The Mathematical Intelligencer . 22 (3): 6–19. doi :10.1007/BF03025276. S2CID  121427433.
• Lorenz, Edward N. (1960). "La predicción estadística de soluciones de ecuaciones dinámicas" (PDF) . Simposio sobre predicción numérica del tiempo en Tokio . Archivado desde el original (PDF) el 23 de mayo de 2019. Consultado el 16 de septiembre de 2020 .

• GA Leonov y NV Kuznetsov (2015). "Sobre diferencias y similitudes en el análisis de los sistemas de Lorenz, Chen y Lu". Matemáticas Aplicadas y Computación . 256 : 334–343. arXiv : 1409.8649 . doi : 10.1016/j.amc.2014.12.132 .
• Pchelintsev, AN (2022). "Sobre un método de alta precisión para estudiar atractores de sistemas dinámicos y sistemas de tipo explosivo". Matemáticas . 10 (8): 1207. arXiv : 2206.08195 . doi : 10.3390/math10081207 .

Wikimedia Commons alberga una categoría multimedia sobre Atractores de Lorenz .

• "Atractor de Lorenz", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Atractor de Lorenzo". MundoMatemático .
• Atractor de Lorenz por Rob Morris, Proyecto de Demostraciones Wolfram .
• Ecuación de Lorenz Archivado el 7 de junio de 2009 en Wayback Machine en planetmath.org
• Caos sincronizado y comunicaciones privadas, con Kevin Cuomo. La implementación del atractor de Lorenz en un circuito electrónico.
• Animación interactiva del atractor de Lorenz (necesita el complemento Adobe Shockwave)
• Atractores 3D: Programa para Mac para visualizar y explorar el atractor de Lorenz en 3 dimensiones
• Atractor de Lorenz implementado en electrónica analógica
• Animación interactiva del atractor de Lorenz (implementada en Ada con GTK+. Fuentes y ejecutable)
• Atractor de Lorenz interactivo basado en la web creado con yoduro