Efecto termoeléctrico

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Efecto termoeléctrico» – noticias  · periódicos  · libros  · académico  · JSTOR ( noviembre de 2019 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Thermoelectric effect
Principles Thermoelectric effect Seebeck effect Peltier effect Thomson effect Seebeck coefficient Ettingshausen effect Nernst effect
Applications Thermoelectric materials Thermocouple Thermopile Thermoelectric cooling Thermoelectric generator Radioisotope thermoelectric generator Automotive thermoelectric generator
v t e

El efecto termoeléctrico es la conversión directa de las diferencias de temperatura en voltaje eléctrico y viceversa a través de un termopar . ^[1] Un dispositivo termoeléctrico crea un voltaje cuando hay una temperatura diferente en cada lado. Por el contrario, cuando se le aplica un voltaje, el calor se transfiere de un lado al otro, creando una diferencia de temperatura.

Este efecto se puede utilizar para generar electricidad , medir la temperatura o cambiar la temperatura de los objetos. Debido a que la dirección del calentamiento y el enfriamiento se ve afectada por el voltaje aplicado, los dispositivos termoeléctricos se pueden utilizar como controladores de temperatura.

El término "efecto termoeléctrico" engloba tres efectos identificados por separado: el efecto Seebeck (las diferencias de temperatura provocan fuerzas electromotrices), el efecto Peltier (los termopares crean diferencias de temperatura) y el efecto Thomson (el coeficiente Seebeck varía con la temperatura). Los efectos Seebeck y Peltier son manifestaciones diferentes del mismo proceso físico; los libros de texto pueden referirse a este proceso como el efecto Peltier-Seebeck (la separación deriva de los descubrimientos independientes del físico francés Jean Charles Athanase Peltier y el físico alemán báltico Thomas Johann Seebeck ). El efecto Thomson es una extensión del modelo Peltier-Seebeck y se le atribuye a Lord Kelvin .

El calentamiento Joule , el calor que se genera cuando una corriente pasa a través de un material conductor , no suele denominarse efecto termoeléctrico. Los efectos Peltier-Seebeck y Thomson son termodinámicamente reversibles , ^[2] mientras que el calentamiento Joule no lo es.

A escala atómica, un gradiente de temperatura hace que los portadores de carga en el material se difundan desde el lado caliente al lado frío. Esto se debe a que las partículas portadoras de carga tienen velocidades medias más altas (y, por lo tanto, energía cinética ) a temperaturas más altas, lo que las lleva a migrar en promedio hacia el lado más frío, en el proceso de transportar calor a través del material. ^[3]

Dependiendo de las propiedades del material y la naturaleza de los portadores de carga (ya sean huecos positivos en un material a granel o electrones de carga negativa), el calor puede transportarse en cualquier dirección con respecto al voltaje. Los semiconductores de tipo n y tipo p a menudo se combinan en serie, ya que tienen direcciones opuestas para el transporte de calor, como lo especifica el signo de sus coeficientes de Seebeck . ^[4]

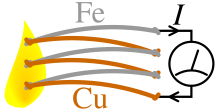
El efecto Seebeck es la fuerza electromotriz (fem) que se desarrolla entre dos puntos de un material conductor de electricidad cuando hay una diferencia de temperatura entre ellos. La fem se denomina fem Seebeck (o fem termo/térmica/termoeléctrica). La relación entre la fem y la diferencia de temperatura es el coeficiente Seebeck. Un termopar mide la diferencia de potencial entre un extremo caliente y uno frío para dos materiales diferentes. Esta diferencia de potencial es proporcional a la diferencia de temperatura entre los extremos caliente y frío. Descubierto por primera vez en 1794 por el científico italiano Alessandro Volta , ^{[5] [nota 1]} recibe su nombre del físico alemán báltico nacido en Rusia Thomas Johann Seebeck, quien lo redescubrió en 1821.

Seebeck observó lo que llamó "efecto termomagnético", en el que la aguja de una brújula magnética se desviaba por un bucle cerrado formado por dos metales diferentes unidos en dos lugares, con una diferencia de temperatura aplicada entre las uniones. El físico danés Hans Christian Ørsted observó que la diferencia de temperatura estaba, de hecho, impulsando una corriente eléctrica, siendo la generación de un campo magnético una consecuencia indirecta, y por eso acuñó el término más preciso "termoelectricidad". ^[6]

El efecto Seebeck es un ejemplo clásico de fuerza electromotriz (FEM) y genera corrientes o voltajes medibles de la misma manera que cualquier otra FEM. La densidad de corriente local se expresa mediante

$${\displaystyle \mathbf {J} =\sigma (-\nabla V+\mathbf {E} _{\text{emf}}),}$$

donde es el voltaje local , ^[7] y es la conductividad local . En general, el efecto Seebeck se describe localmente mediante la creación de un campo electromotriz.${\displaystyle V}$${\displaystyle \sigma }$

$${\displaystyle \mathbf {E} _{\text{emf}}=-S\nabla T,}$$

donde es el coeficiente de Seebeck (también conocido como termopotencia), una propiedad del material local, y es el gradiente de temperatura.${\displaystyle S}$${\displaystyle \nabla T}$

Los coeficientes Seebeck varían generalmente en función de la temperatura y dependen en gran medida de la composición del conductor. Para materiales comunes a temperatura ambiente, el coeficiente Seebeck puede tener un valor que va desde -100 μV/K hasta +1000 μV/K (consulte el artículo sobre el coeficiente Seebeck para obtener más información).

En la práctica, los efectos termoeléctricos son esencialmente inobservables en un punto caliente o frío localizado en un único material conductor homogéneo, ya que las fem totales de los gradientes de temperatura crecientes y decrecientes se cancelarán perfectamente. Colocar un electrodo en el punto caliente para intentar medir el voltaje desplazado localmente solo tendrá éxito parcialmente: significa que aparecerá otro gradiente de temperatura dentro del electrodo y, por lo tanto, la fem total dependerá de la diferencia en los coeficientes Seebeck entre el electrodo y el conductor al que está conectado.

Los termopares están formados por dos cables, cada uno de un material diferente, que se unen eléctricamente en una región de temperatura desconocida. Los extremos sueltos se miden en un estado de circuito abierto (sin corriente ). Aunque los coeficientes Seebeck de los materiales dependen de forma no lineal de la temperatura y son diferentes para los dos materiales, la condición de circuito abierto significa que en todas partes. Por lo tanto (consulte el artículo sobre termopares para obtener más detalles), el voltaje medido en los extremos sueltos de los cables depende directamente de la temperatura desconocida y, sin embargo, es totalmente independiente de otros detalles como la geometría exacta de los cables. Esta relación directa permite que la disposición del termopar se utilice como un termómetro sencillo sin calibrar, siempre que se conozca la diferencia en las curvas -vs- de los dos materiales y la temperatura de referencia en los extremos sueltos de los cables medidos.${\displaystyle \mathbf {J} =0}$${\displaystyle S}$${\displaystyle \nabla V=-S\nabla T}$${\displaystyle S}$${\displaystyle T}$

La clasificación termoeléctrica funciona de manera similar a un termopar, pero implica un material desconocido en lugar de una temperatura desconocida: una sonda metálica de composición conocida se mantiene a una temperatura constante conocida y se mantiene en contacto con la muestra desconocida que se calienta localmente a la temperatura de la sonda, lo que proporciona una medición aproximada del coeficiente Seebeck desconocido . Esto puede ayudar a distinguir entre diferentes metales y aleaciones.${\displaystyle S}$

Las termopilas se forman a partir de muchos termopares en serie, que se mueven en zigzag entre el calor y el frío, lo que multiplica la salida de voltaje.

Los generadores termoeléctricos son como un termopar o una termopila, pero extraen algo de corriente del voltaje generado para extraer energía de los diferenciales de calor. Están optimizados de manera diferente a los termopares, ya que utilizan materiales termoeléctricos de alta calidad en una disposición de termopila para maximizar la energía extraída. Aunque no son particularmente eficientes, estos generadores tienen la ventaja de no tener partes móviles.

This section needs expansion. You can help by adding to it. (October 2024)

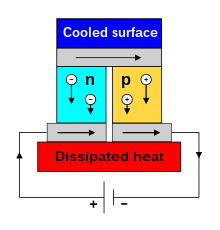
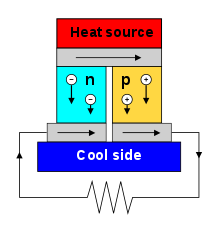
Cuando una corriente eléctrica pasa a través de un circuito de un termopar , se genera calor en una unión y se absorbe en la otra unión. Esto se conoce como el efecto Peltier : la presencia de calor o enfriamiento en una unión electrificada de dos conductores diferentes. El efecto recibe su nombre del físico francés Jean Charles Athanase Peltier , quien lo descubrió en 1834. ^[8] Cuando se hace fluir una corriente a través de una unión entre dos conductores, A y B, se puede generar o eliminar calor en la unión. El calor Peltier generado en la unión por unidad de tiempo es

$${\displaystyle {\dot {Q}}=(\Pi _{\text{A}}-\Pi _{\text{B}})I,}$$

donde y son los coeficientes Peltier de los conductores A y B, y es la corriente eléctrica (de A a B). El calor total generado no está determinado únicamente por el efecto Peltier, ya que también puede verse influenciado por el calentamiento Joule y los efectos del gradiente térmico (ver más abajo).${\displaystyle \Pi _{\text{A}}}$${\displaystyle \Pi _{\text{B}}}$${\displaystyle I}$

Los coeficientes Peltier representan la cantidad de calor transportado por unidad de carga. Dado que la corriente de carga debe ser continua a través de una unión, el flujo de calor asociado desarrollará una discontinuidad si y son diferentes. El efecto Peltier puede considerarse como la contraparte de la acción inversa del efecto Seebeck (análogo a la fuerza contraelectromotriz en la inducción magnética): si se cierra un circuito termoeléctrico simple, entonces el efecto Seebeck impulsará una corriente, que a su vez (por el efecto Peltier) siempre transferirá calor de la unión caliente a la fría. La estrecha relación entre los efectos Peltier y Seebeck se puede ver en la conexión directa entre sus coeficientes: (ver a continuación).${\displaystyle \Pi _{\text{A}}}$${\displaystyle \Pi _{\text{B}}}$${\displaystyle \Pi =TS}$

Una bomba de calor Peltier típica consta de varias uniones en serie, a través de las cuales circula una corriente. Algunas de las uniones pierden calor debido al efecto Peltier, mientras que otras lo ganan. Las bombas de calor termoeléctricas aprovechan este fenómeno, al igual que los dispositivos de refrigeración termoeléctricos que se encuentran en los refrigeradores.

El efecto Peltier se puede utilizar para crear una bomba de calor . Cabe destacar que el refrigerador termoeléctrico Peltier es un refrigerador compacto que no tiene fluido circulante ni partes móviles. Estos refrigeradores son útiles en aplicaciones donde sus ventajas superan la desventaja de su muy baja eficiencia.

Otras aplicaciones de bombas de calor, como los deshumidificadores, también pueden utilizar bombas de calor Peltier.

Los refrigeradores termoeléctricos son trivialmente reversibles, ya que se pueden usar como calentadores simplemente invirtiendo la corriente. A diferencia del calentamiento eléctrico resistivo ordinario ( calentamiento Joule ) que varía con el cuadrado de la corriente, el efecto de calentamiento termoeléctrico es lineal en la corriente (al menos para corrientes pequeñas) pero requiere un disipador frío para reponer la energía térmica. Este rápido efecto de calentamiento y enfriamiento reversible es utilizado por muchos termocicladores modernos , dispositivos de laboratorio utilizados para amplificar ADN mediante la reacción en cadena de la polimerasa (PCR). La PCR requiere el calentamiento y enfriamiento cíclico de las muestras a temperaturas específicas. La inclusión de muchos termopares en un espacio pequeño permite que se amplifiquen muchas muestras en paralelo.

En el caso de determinados materiales, el coeficiente de Seebeck no es constante en temperatura, por lo que un gradiente espacial de temperatura puede dar lugar a un gradiente en el coeficiente de Seebeck. Si se hace pasar una corriente a través de este gradiente, se producirá una versión continua del efecto Peltier. Este efecto Thomson fue predicho y observado posteriormente en 1851 por Lord Kelvin (William Thomson). ^[9] Describe el calentamiento o enfriamiento de un conductor que transporta corriente con un gradiente de temperatura. Si se hace pasar una densidad de corriente a través de un conductor homogéneo, el efecto Thomson predice una tasa de producción de calor por unidad de volumen.${\displaystyle \mathbf {J} }$

$${\displaystyle {\dot {q}}=-{\mathcal {K}}\mathbf {J} \cdot \nabla T,}$$

donde es el gradiente de temperatura, y es el coeficiente de Thomson. El efecto Thomson es una manifestación de la dirección del flujo de portadores eléctricos con respecto a un gradiente de temperatura dentro de un conductor. Estos absorben energía (calor) que fluye en una dirección opuesta a un gradiente térmico, aumentando su energía potencial y, cuando fluyen en la misma dirección que un gradiente térmico, liberan calor, disminuyendo su energía potencial. ^[10] El coeficiente de Thomson está relacionado con el coeficiente de Seebeck como (ver más abajo). Esta ecuación, sin embargo, descuida el calentamiento Joule y la conductividad térmica ordinaria (ver ecuaciones completas más abajo).${\displaystyle \nabla T}$${\displaystyle {\mathcal {K}}}$${\displaystyle {\mathcal {K}}=T{\tfrac {dS}{dT}}}$

A menudo, en el funcionamiento de un dispositivo termoeléctrico real intervienen más de uno de los efectos anteriores. El efecto Seebeck, el efecto Peltier y el efecto Thomson se pueden agrupar de forma coherente y rigurosa, como se describe aquí; esto también incluye los efectos del calentamiento Joule y la conducción de calor ordinaria. Como se indicó anteriormente, el efecto Seebeck genera una fuerza electromotriz, lo que conduce a la ecuación de corriente ^[11].

$${\displaystyle \mathbf {J} =\sigma (-{\boldsymbol {\nabla }}V-S\nabla T).}$$

Para describir los efectos Peltier y Thomson, debemos considerar el flujo de energía. Si la temperatura y la carga cambian con el tiempo, la ecuación termoeléctrica completa para la acumulación de energía, , es ^[11]${\displaystyle {\dot {e}}}$

$${\displaystyle {\dot {e}}=\nabla \cdot (\kappa \nabla T)-\nabla \cdot (V+\Pi )\mathbf {J} +{\dot {q}}_{\text{ext}},}$$

donde es la conductividad térmica . El primer término es la ley de conducción de calor de Fourier y el segundo término muestra la energía transportada por las corrientes. El tercer término, , es el calor añadido desde una fuente externa (si corresponde).${\displaystyle \kappa }$${\displaystyle {\dot {q}}_{\text{ext}}}$

Si el material ha alcanzado un estado estable, las distribuciones de carga y temperatura son estables, por lo que y . Utilizando estos hechos y la segunda relación de Thomson (ver a continuación), la ecuación del calor se puede simplificar a${\displaystyle {\dot {e}}=0}$${\displaystyle \nabla \cdot \mathbf {J} =0}$

$${\displaystyle -{\dot {q}}_{\text{ext}}=\nabla \cdot (\kappa \nabla T)+\mathbf {J} \cdot \left(\sigma ^{-1}\mathbf {J} \right)-T\mathbf {J} \cdot \nabla S.}$$

El término medio es el calentamiento Joule, y el último término incluye los efectos Peltier ( en la unión) y Thomson ( en el gradiente térmico). Combinado con la ecuación de Seebeck para , esto se puede utilizar para resolver los perfiles de voltaje y temperatura en estado estable en un sistema complicado.${\displaystyle \nabla S}$${\displaystyle \nabla S}$${\displaystyle \mathbf {J} }$

Si el material no está en un estado estable, una descripción completa debe incluir efectos dinámicos como los relacionados con la capacitancia eléctrica , la inductancia y la capacidad térmica .

Los efectos termoeléctricos quedan fuera del ámbito de la termodinámica del equilibrio. Implican necesariamente flujos continuos de energía. Implican, al menos, tres cuerpos o subsistemas termodinámicos, dispuestos de una manera particular, junto con una disposición especial del entorno. Los tres cuerpos son los dos metales diferentes y su región de unión. La región de unión es un cuerpo no homogéneo, que se supone estable, que no sufre amalgamación por difusión de materia. El entorno está dispuesto para mantener dos depósitos de temperatura y dos depósitos eléctricos.

Para que se produzca un equilibrio termodinámico imaginario, pero no realmente posible, sería necesario evitar la transferencia de calor del depósito caliente al depósito frío mediante una diferencia de voltaje específicamente coincidente mantenida por los depósitos eléctricos, y la corriente eléctrica debería ser cero. Para que haya un estado estable, debe haber al menos alguna transferencia de calor o alguna corriente eléctrica distinta de cero. Los dos modos de transferencia de energía, como calor y como corriente eléctrica, se pueden distinguir cuando hay tres cuerpos distintos y una disposición distinta de los alrededores.

Sin embargo, en el caso de una variación continua del medio, no es posible distinguir de forma unívoca la transferencia de calor y el trabajo termodinámico . Esto es más complicado que los procesos termodinámicos que se suelen considerar, en los que sólo se conectan dos subsistemas homogéneos respectivamente.

En 1854, Lord Kelvin encontró relaciones entre los tres coeficientes, lo que implica que los efectos Thomson, Peltier y Seebeck son manifestaciones diferentes de un efecto (caracterizado únicamente por el coeficiente Seebeck). ^[12]

La primera relación de Thomson es ^[11]

$${\displaystyle {\mathcal {K}}\equiv {\frac {d\Pi }{dT}}-S,}$$

donde es la temperatura absoluta, es el coeficiente de Thomson, es el coeficiente de Peltier y es el coeficiente de Seebeck. Esta relación se demuestra fácilmente dado que el efecto Thomson es una versión continua del efecto Peltier.${\displaystyle T}$${\displaystyle {\mathcal {K}}}$${\displaystyle \Pi }$${\displaystyle S}$

La segunda relación de Thomson es

$${\displaystyle \Pi =TS.}$$

Esta relación expresa una conexión sutil y fundamental entre los efectos Peltier y Seebeck. No se demostró satisfactoriamente hasta la aparición de las relaciones de Onsager , y vale la pena señalar que esta segunda relación de Thomson solo está garantizada para un material simétrico con inversión temporal; si el material se coloca en un campo magnético o está ordenado magnéticamente ( ferromagnético , antiferromagnético , etc.), entonces la segunda relación de Thomson no toma la forma simple que se muestra aquí. ^[13]

Ahora, utilizando la segunda relación, la primera relación de Thomson se convierte en

$${\displaystyle {\mathcal {K}}=T{\tfrac {dS}{dT}}}$$

El coeficiente de Thomson es único entre los tres coeficientes termoeléctricos principales porque es el único que se puede medir directamente para materiales individuales. Los coeficientes de Peltier y Seebeck solo se pueden determinar fácilmente para pares de materiales; por lo tanto, es difícil encontrar valores absolutos de coeficientes Seebeck o Peltier para un material individual.

Si se mide el coeficiente de Thomson de un material en un amplio rango de temperaturas, se puede integrar utilizando las relaciones de Thomson para determinar los valores absolutos de los coeficientes de Peltier y Seebeck. Esto solo se debe hacer para un material, ya que los otros valores se pueden determinar midiendo los coeficientes Seebeck por pares en termopares que contienen el material de referencia y luego agregando nuevamente el coeficiente Seebeck absoluto del material de referencia. Para obtener más detalles sobre la determinación del coeficiente Seebeck absoluto, consulte Coeficiente Seebeck .

• Material barocalórico
• Efecto Nernst : un fenómeno termoeléctrico en el que una muestra permite la conducción eléctrica en un campo magnético y un gradiente de temperatura normal (perpendicular) entre sí.
• Efecto Ettingshausen : fenómeno termoeléctrico que afecta la corriente en un conductor en un campo magnético.
• Piroelectricidad : la creación de una polarización eléctrica en un cristal después de calentarlo o enfriarlo, un efecto distinto de la termoelectricidad.
• Emisión termoiónica : liberación de partículas cargadas de un electrodo caliente.
• Celda termogalvánica : producción de energía eléctrica a partir de una celda galvánica con electrodos a diferentes temperaturas.
• Termopila
• Termofotovoltaica : producción de energía eléctrica a partir de energía térmica utilizando el efecto fotovoltaico.

Wikimedia Commons alberga una categoría multimedia sobre Termoelectricidad .

• Sociedad Termoeléctrica Internacional
• Föll, Helmut (octubre de 2019). "2.3.3 Efectos termoeléctricos: consideraciones generales". Materiales electrónicos . Universidad de Kiel.
• Un artículo de noticias sobre los aumentos en la eficiencia del diodo térmico.