Distorsión (óptica)

En óptica geométrica , la distorsión es una desviación de la proyección rectilínea ; una proyección en la que las líneas rectas de una escena permanecen rectas en una imagen. Es una forma de aberración óptica que se puede distinguir de otras aberraciones como la aberración esférica , el coma , la aberración cromática , la curvatura de campo y el astigmatismo en el sentido de que estas afectan la nitidez de la imagen sin cambiar la forma o la estructura de un objeto en la imagen (por ejemplo, una línea recta en un objeto sigue siendo una línea recta en la imagen aunque la nitidez de la imagen puede degradarse por las aberraciones mencionadas), mientras que la distorsión puede cambiar la estructura del objeto en la imagen (lo que se denomina distorsión).

Aunque la distorsión puede ser irregular o seguir muchos patrones, las distorsiones más comunes son las simétricas radiales, o aproximadamente simétricas, que surgen de la simetría de una lente fotográfica . Estas distorsiones radiales generalmente se pueden clasificar como distorsiones de barril o distorsiones de cojín . ^[1]

Distorsión de barril

En la distorsión de barril, la ampliación de la imagen disminuye con la distancia desde el eje óptico . El efecto aparente es una imagen que parece estar mapeada alrededor de una esfera (o barril ). Las lentes de ojo de pez , que toman vistas hemisféricas, utilizan este tipo de distorsión como una forma de mapear un plano de objeto infinitamente ancho en un área de imagen finita. En una lente con zoom , la distorsión de barril aparece en el medio del rango de longitud focal de la lente y es peor en el extremo gran angular del rango. ^[2] Las lentes esféricas cóncavas (menos) tienden a tener distorsión de barril.

Distorsión de acerico

En la distorsión de cojín, la ampliación de la imagen aumenta con la distancia desde el eje óptico . El efecto visible es que las líneas que no pasan por el centro de la imagen se curvan hacia adentro, hacia el centro de la imagen, como un cojín . Las lentes esféricas convexas (plus) tienden a tener una distorsión de cojín.

Distorsión del bigote

Una mezcla de ambos tipos, a veces denominada distorsión de bigote ( moustache dysfunction ) o distorsión compleja , es menos común pero no rara. Comienza como una distorsión de barril cerca del centro de la imagen y gradualmente se convierte en una distorsión de cojín hacia la periferia de la imagen, haciendo que las líneas horizontales en la mitad superior del marco parezcan un bigote de manillar .

Matemáticamente, la distorsión de barril y la distorsión de cojín son cuadráticas , lo que significa que aumentan con el cuadrado de la distancia desde el centro. En la distorsión de bigote, el término cuártico (grado 4) es significativo: en el centro, la distorsión de barril de grado 2 es dominante, mientras que en el borde domina la distorsión de grado 4 en la dirección del cojín. En principio, son posibles otras distorsiones (cojín en el centro y barril en el borde, o distorsiones de orden superior (grado 6, grado 8), pero generalmente no ocurren en lentes prácticas, y las distorsiones de orden superior son pequeñas en relación con los efectos principales de barril y cojín.

Los nombres de estas distorsiones provienen de objetos familiares que son visualmente similares.

• 
  En la distorsión de barril, las líneas rectas sobresalen hacia afuera en el centro, como en un barril .
• 
  En la distorsión de acerico, las esquinas de los cuadrados forman puntas alargadas, como en un cojín .
• 
  En la distorsión del bigote, las líneas horizontales se abultan en el centro y luego se doblan hacia el otro lado a medida que se acercan al borde del marco (si están en la parte superior del marco), como en los bigotes de manillar rizados .

En fotografía, la distorsión se asocia particularmente con los lentes zoom , en particular los zoom de gran alcance, pero también puede encontrarse en lentes prime y depende de la distancia focal; por ejemplo, el Canon EF 50 mm. y​1.4 presenta distorsión de barril a distancias focales extremadamente cortas. La distorsión de barril se puede encontrar en lentes gran angular y, a menudo, se ve en el extremo gran angular de los lentes zoom, mientras que la distorsión de cojín se ve a menudo en lentes telefoto más antiguas o de gama baja . La distorsión de bigote se observa particularmente en el extremo gran angular de los zooms, con ciertos lentes retrofoco y, más recientemente, en zooms de gran alcance como el Nikon 18-200 mm.

Una cierta cantidad de distorsión de cojín se encuentra a menudo en los instrumentos ópticos visuales, por ejemplo, los binoculares , donde sirve para contrarrestar el efecto globo .

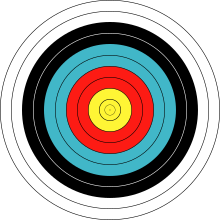
Para entender estas distorsiones, hay que recordar que se trata de defectos radiales ; los sistemas ópticos en cuestión tienen simetría rotacional (omitiendo los defectos no radiales), por lo que la imagen de prueba didácticamente correcta sería un conjunto de círculos concéntricos con una separación uniforme, como el objetivo de un tirador. Se observará entonces que estas distorsiones comunes implican en realidad una asignación de radio no lineal del objeto a la imagen: lo que parece una distorsión de cojín, en realidad es simplemente una asignación de radio exagerada para radios grandes en comparación con radios pequeños. Un gráfico que muestra transformaciones de radio (de objeto a imagen) será más pronunciado en el extremo superior (extremo derecho). Por el contrario, la distorsión de barril es en realidad una asignación de radio disminuida para radios grandes en comparación con radios pequeños. Un gráfico que muestra transformaciones de radio (de objeto a imagen) será menos pronunciado en el extremo superior (extremo derecho).

La distorsión radial que depende de la longitud de onda se denomina " aberración cromática lateral " (lateral porque es radial y cromática porque depende del color [longitud de onda]). Puede provocar franjas de color en áreas de alto contraste en las partes externas de la imagen. No debe confundirse con la aberración cromática axial (longitudinal), que provoca aberraciones en todo el campo, en particular franjas de color púrpura .

La distorsión radial, aunque está dominada principalmente por componentes radiales de orden bajo, ^[3] se puede corregir utilizando el modelo de distorsión de Brown, ^[4] también conocido como el modelo Brown-Conrady basado en trabajos anteriores de Conrady. ^[5] El modelo Brown-Conrady corrige tanto la distorsión radial como la distorsión tangencial causada por elementos físicos en una lente que no están perfectamente alineados. Esta última también se conoce como distorsión de descentrado . Consulte Zhang ^[6] para obtener una discusión adicional sobre la distorsión radial. El modelo de distorsión Brown-Conrady es

$${\displaystyle {\begin{alignedat}{3}x_{\mathrm {u} }=x_{\mathrm {d} }&+(x_{\mathrm {d} }-x_{\mathrm {c} }) (K_{1}r^{2}+K_{2}r^{4}+\cdots )+(P_{1}(r^{2}+2(x_{\mathrm {d} }-x_{ \mathrm {c} })^{2})\\&+2P_{2}(x_{\mathrm {d} }-x_{\mathrm {c} })(y_{\mathrm {d} }-y_ {\mathrm {c} }))(1+P_{3}r^{2}+P_{4}r^{4}\cdots )\\y_{\mathrm {u} }=y_{\mathrm {d} }&+(y_{\mathrm {d} }-y_{\mathrm {c} })(K_{1}r^{2}+K_{2}r^{4}+\cdots )+ (2P_{1}(x_{\mathrm {d} }-x_{\mathrm {c} })(y_{\mathrm {d} }-y_{\mathrm {c} })\\&+P_{2 }(r^{2}+2(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}))(1+P_{3}r^{2}+P_{4 }r^{4}\cdots ),\end{alignedat}}}$$

dónde

• ${\displaystyle (x_{\mathrm {d} },\ y_{\mathrm {d} })}$es el punto de imagen distorsionado tal como se proyecta en el plano de la imagen utilizando una lente especificada;
• ${\displaystyle (x_{\mathrm {u} },\ y_{\mathrm {u} })}$es el punto de imagen no distorsionado tal como lo proyecta una cámara estenopeica ideal ;
• ${\displaystyle (x_{\mathrm {c} },\ y_{\mathrm {c} })}$es el centro de distorsión;
• $Estilo de visualización K_{n}$es el coeficiente de distorsión radial;${\displaystyle n^{\mathrm {th} }}$
• $Estilo de visualización P_{n}$es el coeficiente de distorsión tangencial; y${\displaystyle n^{\mathrm {th} }}$
• ${\estilo de visualización r}$= , la distancia euclidiana entre el punto de la imagen distorsionada y el centro de distorsión. ^[3]${\displaystyle {\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} }) ^{2}}}}$

La distorsión de barril normalmente tendrá un término negativo, mientras que la distorsión de cojín tendrá un valor positivo. La distorsión de bigote tendrá una serie geométrica radial no monótona donde para algunos la secuencia cambiará de signo.$Estilo de visualización K_{1}$${\estilo de visualización r}$

Para modelar la distorsión radial, el modelo de división ^[7] generalmente proporciona una aproximación más precisa que el modelo polinomial de orden par de Brown-Conrady, ^[8]

$${\displaystyle {\begin{aligned}x_{\mathrm {u} }&=x_{\mathrm {c} }+{\frac {x_{\mathrm {d} }-x_{\mathrm {c} }} {1+K_{1}r^{2}+K_{2}r^{4}+\cdots }}\\y_{\mathrm {u} }&=y_{\mathrm {c} }+{\ frac {y_{\mathrm {d} }-y_{\mathrm {c} }}{1+K_{1}r^{2}+K_{2}r^{4}+\cdots }},\end {alineado}}}$$

Utilizando los mismos parámetros definidos previamente. Para la distorsión radial, este modelo de división suele preferirse al modelo Brown-Conrady, ya que requiere menos términos para describir con mayor precisión la distorsión severa. ^[8] Utilizando este modelo, un solo término suele ser suficiente para modelar la mayoría de las cámaras. ^[9]

El software puede corregir esas distorsiones deformando la imagen con una distorsión inversa. Esto implica determinar qué píxel distorsionado corresponde a cada píxel no distorsionado, lo que no es trivial debido a la no linealidad de la ecuación de distorsión. ^[3] La aberración cromática lateral (franjas violeta/verde) se puede reducir significativamente aplicando dicha deformación para el rojo, el verde y el azul por separado.

Para distorsionar o desdistorsionar se necesitan ambos conjuntos de coeficientes o invertir el problema no lineal, que, en general, carece de una solución analítica. Se pueden utilizar métodos estándar, como la aproximación, la linealización local y los solucionadores iterativos. El solucionador que se prefiera dependerá de la precisión requerida y de los recursos computacionales disponibles.

Además de ser generalmente suficiente para modelar la mayoría de las cámaras, como se mencionó, el modelo de división de un solo término tiene una solución analítica para el problema de distorsión inversa. ^[8] En este caso, los píxeles distorsionados se dan por

$${\displaystyle {\begin{aligned}x_{\mathrm {d} }&=x_{\mathrm {c} }+{\frac {x_{\mathrm {u} }-x_{\mathrm {c} }} {2K_{1}r_{u}^{2}}}(1-{\sqrt {1-4K_{1}r_{u}^{2}}})\\y_{\mathrm {d} }& =y_{\mathrm {c} }+{\frac {y_{\mathrm {u} }-y_{\mathrm {c} }}{2K_{1}r_{u}^{2}}}(1- {\sqrt {1-4K_{1}r_{u}^{2}}}),\end{aligned}}}$$

dónde

• ${\displaystyle r_{u}}$= , la distancia euclidiana entre el punto de la imagen no distorsionada y el centro de distorsión/no distorsión.${\displaystyle {\sqrt {(x_{\mathrm {u} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {u} }-y_{\mathrm {c} })^{2}}}}$

El software calibrado funciona a partir de una tabla de funciones de transferencia de lente/cámara:

• Adobe Photoshop Lightroom y Photoshop CS5 pueden corregir distorsiones complejas.
• PTlens es un complemento o una aplicación independiente de Photoshop que corrige distorsiones complejas. No solo corrige distorsiones lineales, sino también componentes no lineales de segundo grado y superiores. ^[10]
• Lensfun es una base de datos y biblioteca de uso gratuito para corregir la distorsión de las lentes. ^{[11] [12]}
• OpenCV es una biblioteca de código abierto con licencia BSD para visión artificial (multilenguaje, multisistema operativo). Incluye un módulo para calibración de cámaras. ^[13]
• El software PhotoLab de DxO puede corregir distorsiones complejas y tiene en cuenta la distancia de enfoque.
• proDAD Defishr incluye una herramienta de desdoblado y una herramienta de calibración. Debido a la distorsión de un patrón de tablero de ajedrez, se calcula el desdoblamiento necesario.
• Las cámaras y lentes del sistema Micro Four Thirds realizan una corrección automática de la distorsión mediante parámetros de corrección que se almacenan en el firmware de cada lente y que son aplicados automáticamente por la cámara y el software de conversión de archivos RAW . La óptica de la mayoría de estas lentes presenta una distorsión sustancialmente mayor que sus contrapartes en sistemas que no ofrecen tales correcciones automáticas, pero las imágenes finales corregidas por software muestran una distorsión notablemente menor que los diseños de la competencia. ^[14]

El software manual permite el ajuste manual de los parámetros de distorsión:

• ImageMagick puede corregir varias distorsiones; por ejemplo, la distorsión de ojo de pez de la popular cámara GoPro Hero3+ Silver se puede corregir con el comando ^[15]

convert distorted_image.jpg -distort barrel "0.06335 -0.18432 -0.13009" corrected_image.jpg

• Photoshop CS2 y Photoshop Elements (a partir de la versión 5) incluyen un filtro de corrección de lente manual para distorsión simple (de cojín/de barril)
• Corel Paint Shop Pro Photo incluye un efecto de distorsión de lente manual para distorsiones simples (barril, ojo de pez, ojo de pez esférico y cojín).
• GIMP incluye corrección manual de la distorsión de la lente (a partir de la versión 2.4).
• PhotoPerfect tiene funciones interactivas para el ajuste general del acerico y para los flecos (ajuste del tamaño de las partes roja, verde y azul de la imagen).
• Hugin se puede utilizar para corregir la distorsión, aunque esa no es su aplicación principal. ^[16]

Además de estos sistemas que abordan las imágenes, hay algunos que también ajustan los parámetros de distorsión de los vídeos:

• FFMPEG utilizando el filtro de vídeo "corrección de lente". ^[17]
• Blender utiliza el editor de nodos para insertar un nodo "Distorsionar/Distorsión de lente" entre los nodos de entrada y salida.

La distorsión radial es un fallo de la lente en su capacidad de ser rectilínea : un fallo en la representación de líneas dentro de líneas. Si una fotografía no se toma en línea recta, incluso con una lente rectilínea perfecta, los rectángulos aparecerán como trapecios : las líneas se representan como líneas, pero los ángulos entre ellas no se conservan (la inclinación no es un mapa conforme ). Este efecto se puede controlar utilizando una lente de control de perspectiva o se puede corregir en el posprocesamiento.

Debido a la perspectiva , las cámaras toman la imagen de un cubo como un tronco de pirámide ( una pirámide truncada con lados trapezoidales) – el extremo más alejado es más pequeño que el más cercano. Esto crea perspectiva, y la velocidad a la que se produce este cambio de escala (la rapidez con la que se encogen los objetos más distantes) crea una sensación de profundidad o profundidad en la escena. Esto no se puede cambiar ni corregir con una simple transformación de la imagen resultante, porque requiere información 3D, es decir, la profundidad de los objetos en la escena. Este efecto se conoce como distorsión de la perspectiva ; la imagen en sí no está distorsionada, pero se percibe como distorsionada cuando se ve desde una distancia de visión normal.

Tenga en cuenta que si el centro de la imagen está más cerca que los bordes (por ejemplo, una toma directa de una cara), tanto la distorsión de barril como la distorsión de gran angular (tomar la fotografía desde cerca) aumentan el tamaño del centro, mientras que la distorsión de cojín y la distorsión de telefoto (tomar la fotografía desde lejos) disminuyen el tamaño del centro. Sin embargo, la distorsión radial dobla las líneas rectas (hacia afuera o hacia adentro), mientras que la distorsión de perspectiva no dobla las líneas, y estos son fenómenos distintos. Los lentes de ojo de pez son lentes de gran angular con una fuerte distorsión de barril y, por lo tanto, presentan ambos fenómenos, por lo que los objetos en el centro de la imagen (si se toman desde una distancia corta) se agrandan particularmente: incluso si se corrige la distorsión de barril, la imagen resultante sigue siendo de un lente de gran angular y seguirá teniendo una perspectiva de gran angular.

• Anamorfosis
• Ángulo de visión
• Perspectiva cilíndrica
• Distorsión
• Gradiente de textura
• Visión submarina
• Viñeteado

Wikimedia Commons tiene medios relacionados con Distorsión (óptica) .

• Estimación y corrección de la distorsión de la lente con código fuente y demostración en línea
• Modelado 3D Distorsión de la lente y campo de visión de la cámara en el diseño de CCTV