Filtro biquad digital
Este artículo incluye una lista de referencias generales , pero carece de suficientes citas en línea correspondientes . ( Octubre de 2015 ) |
En el procesamiento de señales , un filtro biquad digital es un filtro lineal recursivo de segundo orden , que contiene dos polos y dos ceros . "Biquad" es una abreviatura de " biquadratic ", que se refiere al hecho de que en el dominio Z , su función de transferencia es la relación de dos funciones cuadráticas :
Los coeficientes suelen normalizarse de forma que 0 = 1:
Los filtros de respuesta al impulso infinito de orden superior pueden ser muy sensibles a la cuantificación de sus coeficientes y pueden volverse inestables fácilmente . Esto es un problema mucho menor con los filtros de primer y segundo orden; por lo tanto, los filtros de orden superior se implementan típicamente como secciones biquad en cascada en serie (y un filtro de primer orden si es necesario). Los dos polos del filtro biquad deben estar dentro del círculo unitario para que sea estable. En general, esto es cierto para todos los filtros discretos, es decir, todos los polos deben estar dentro del círculo unitario en el dominio Z para que el filtro sea estable.
Implementación
Forma directa 1
La implementación más sencilla es la forma directa 1, que tiene la siguiente ecuación diferencial :
o, si se normaliza:
Aquí los coeficientes , y determinan ceros, y , determinan la posición de los polos.
Diagrama de flujo del filtro biquad en forma directa 1:
Cuando estas secciones se conectan en cascada para filtros de orden mayor que 2, se puede mejorar la eficiencia de la implementación al notar que el retraso de la salida de una sección se clona en la entrada de la siguiente sección. Se pueden eliminar dos componentes de retraso de almacenamiento entre secciones.
Forma directa 2
La forma directa 2 implementa la misma función de transferencia normalizada que la forma directa 1, pero en dos partes:
y usando la ecuación diferencial :
Diagrama de flujo del filtro biquad en forma directa 2:
La implementación de la forma directa 2 solo necesita N unidades de retardo, donde N es el orden del filtro, potencialmente la mitad que la forma directa 1. La derivación de la forma directa 1 normalizada es la siguiente:
Supongamos la sustitución:
Lo que resulta en:
Aislando los coeficientes , y :
Suponiendo que se obtiene el resultado anterior:
La desventaja es que la forma directa 2 aumenta la posibilidad de desbordamiento aritmético para filtros de Q alto o resonancia. [1] Se ha demostrado que a medida que Q aumenta, el ruido de redondeo de ambas topologías de forma directa aumenta sin límites. [2] Esto se debe a que, conceptualmente, la señal pasa primero a través de un filtro de todos los polos (que normalmente aumenta la ganancia en las frecuencias resonantes) antes de que el resultado de eso se sature, luego pasa a través de un filtro de todos los ceros (que a menudo atenúa mucho de lo que amplifica la mitad de todos los polos).
La implementación de la forma directa 2 se denomina forma canónica, porque utiliza la mínima cantidad de retrasos, sumadores y multiplicadores, produciendo la misma función de transferencia que la implementación de la forma directa 1.
Formas directas transpuestas
![[icon]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | This section needs expansion. You can help by adding to it. (October 2015) |
Cada una de las dos formas directas se puede transponer invirtiendo el gráfico de flujo sin alterar la función de transferencia. Los puntos de ramificación se cambian por sumadores y los sumadores se cambian por puntos de ramificación. [3] Estos proporcionan implementaciones modificadas que logran la misma función de transferencia que puede ser matemáticamente significativa en una implementación del mundo real donde la precisión se puede perder en el almacenamiento de estados.
Las ecuaciones diferenciales para la forma directa transpuesta 2 son:
dónde
y
Forma directa transpuesta 1
La forma directa 1 se transpone a
se transpone a
Forma directa transpuesta 2
La forma directa 2 se transpone a
se transpone a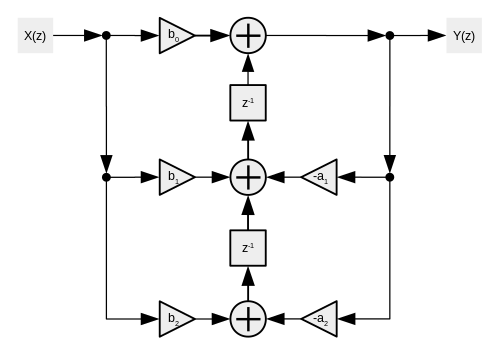
Cuantificación del ruido
Cuando una muestra de n bits se multiplica por un coeficiente de m bits, el producto tiene n+m bits. Estos productos se acumulan típicamente en un registro DSP, la suma de cinco productos puede necesitar 3 bits de desbordamiento; este registro suele ser lo suficientemente grande como para contener n+m+3 bits. El z −1 se implementa almacenando un valor para un tiempo de muestra; este registro de almacenamiento suele tener n bits, el registro acumulador se redondea para que quepan n bits y esto introduce ruido de cuantificación.
En la disposición de forma directa 1, hay una única función de cuantificación/redondeo Q(z):
En la disposición de forma directa 2, también hay una función de cuantificación/redondeo para un valor intermedio. En una cascada, es posible que el valor no necesite redondeo entre etapas, pero el resultado final sí puede necesitarlo.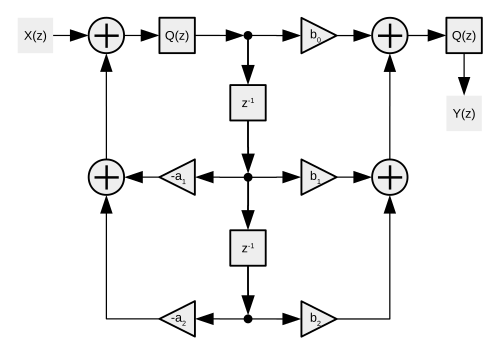
El DSP de punto fijo suele preferir las formas no transpuestas y tiene un acumulador con una gran cantidad de bits, y se redondea cuando se almacena en la memoria principal. El DSP de punto flotante suele preferir la forma transpuesta, cada multiplicación y potencialmente cada adición se redondean; las adiciones son un resultado de mayor precisión, cuando ambos operandos tienen una magnitud similar.
Véase también
Referencias
- ^ JO Smith III, Forma directa II
- ^ LB Jackson, "Sobre la interacción del ruido de redondeo y el rango dinámico en filtros digitales", Bell Sys. Tech. J. , vol. 49 (febrero de 1970), reimpreso en Digital Signal Process , LR Rabiner y CM Rader, Eds. (IEEE Press, Nueva York, 1972).
- ^ "Formas directas transpuestas".
Enlaces externos
- Fórmulas de libro de cocina para los coeficientes del filtro biquad del ecualizador de audio
- WikiLibro sobre procesamiento de señales digitales
- Filtros digitales de segundo orden acoplados



![{\displaystyle \ y[n]={\frac {1}{a_{0}}}\left(b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]-a_{1}y[n-1]-a_{2}y[n-2]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51d2168652d5ce30472257d7d4b94d840ba67beb)
![{\displaystyle \ y[n]=b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]-a_{1}y[n-1] -a_{2}y[n-2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbbed7b550ce5ae4c333653731fd59815f2001fe)







![{\displaystyle \ y[n]=b_{0}w[n]+b_{1}w[n-1]+b_{2}w[n-2],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffd7f716e1296ba7acbe9c1ffa0fe62beba53cfc)
![{\displaystyle \ w[n]=x[n]-a_{1}w[n-1]-a_{2}w[n-2].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c627a74e81ff3ff1736957f11c8337bdc37ab1a)

![{\displaystyle \ y[n]=b_{0}w[n]+b_{1}w[n-1]+b_{2}w[n-2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b6296ed1b6fc3dc8436319871a752d3831041c8)
![{\displaystyle \ y[n]=b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]-a_{1}(b_{0}w[n-1]+b_{1}w[n-2]+b_{2}w[n-3])-a_{2}(b_{0}w[n-2]+b_{1}w[n-3]+b_{2}w[n-4])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c791a3b815b00ed74e88b95149ccaf42ed2565c)
![{\displaystyle \ y[n]=b_{0}(x[n]-a_{1}w[n-1]-a_{2}w[n-2])+b_{1}(x[n-1]-a_{1}w[n-2]-a_{2}w[n-3])+b_{2}(x[n-2]-a_{1}w[n-3]-a_{2}w[n-4])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/885092ae2c83f329ec58a4feb5ed187cc9c18be3)
![{\displaystyle \ w[n]=x[n]-a_{1}w[n-1]-a_{2}w[n-2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b75c1190df12d6c54d24435ff7f917ecff6af44d)
![{\displaystyle \ y[n]=b_{0}x[n]+s_{1}[n-1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/781206a00e173b4bb4c8633fadc817305fb5b40f)
![{\displaystyle \ s_{1}[n]=s_{2}[n-1]+b_{1}x[n]-a_{1}y[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3eabb9aff6fc0dd170bcb5b1cb96f79688ab09b)
![{\displaystyle \ s_{2}[n]=b_{2}x[n]-a_{2}y[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a7ce54b05bb366b4b1b07fc6d6a55fdf8ddd6e8)