Geometría del taxi

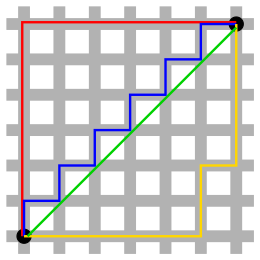
La geometría del taxi o geometría de Manhattan es una geometría en la que se ignora la distancia euclidiana familiar y, en cambio, la distancia entre dos puntos se define como la suma de las diferencias absolutas de sus respectivas coordenadas cartesianas , una función de distancia (o métrica ) llamada distancia del taxi , distancia de Manhattan o distancia de manzana de la ciudad . El nombre se refiere a la isla de Manhattan o, genéricamente, a cualquier ciudad planificada con una cuadrícula rectangular de calles, en la que un taxi solo puede viajar a lo largo de las direcciones de la cuadrícula. En la geometría del taxi, la distancia entre dos puntos cualesquiera es igual a la longitud de su ruta de cuadrícula más corta. Esta definición diferente de distancia también conduce a una definición diferente de la longitud de una curva, para la cual un segmento de línea entre dos puntos cualesquiera tiene la misma longitud que una ruta de cuadrícula entre esos puntos en lugar de su longitud euclidiana.

La distancia en taxi también se conoce como distancia rectilínea o distancia L ¹ (ver espacio L ^p ). ^[1] Esta geometría se ha utilizado en el análisis de regresión desde el siglo XVIII y a menudo se la conoce como LASSO . Su interpretación geométrica data de la geometría no euclidiana del siglo XIX y se debe a Hermann Minkowski .

En el espacio de coordenadas reales bidimensional la distancia en taxi entre dos puntos y es . Es decir, es la suma de los valores absolutos de las diferencias en ambas coordenadas. ${\displaystyle \mathbb {R} ^{2},}$${\displaystyle (x_{1},y_{1})}$${\displaystyle (x_{2},y_{2})}$${\displaystyle \left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|}$

La distancia en taxi, , entre dos puntos en un espacio de coordenadas reales n -dimensional con un sistema de coordenadas cartesianas fijo , es la suma de las longitudes de las proyecciones del segmento de línea entre los puntos sobre los ejes de coordenadas . Más formalmente, Por ejemplo, en , la distancia en taxi entre y es${\displaystyle d_{\text{T}}}$${\displaystyle \mathbf {p} =(p_{1},p_{2},\puntos ,p_{n}){\text{ y }}\mathbf {q} =(q_{1},q_{2},\puntos ,q_{n})}$$${\displaystyle d_{\text{T}}(\mathbf {p} ,\mathbf {q} )=\left\|\mathbf {p} -\mathbf {q} \right\|_{\text{T}}=\sum _{i=1}^{n}\left|p_{i}-q_{i}\right|}$$${\displaystyle \mathbb {R} ^{2}}$${\displaystyle \mathbf {p} =(p_{1},p_{2})}$${\displaystyle \mathbf {q} =(q_{1},q_{2})}$${\displaystyle \left|p_{1}-q_{1}\right|+\left|p_{2}-q_{2}\right|.}$

La métrica L ¹ fue utilizada en el análisis de regresión , como una medida de bondad de ajuste , en 1757 por Roger Joseph Boscovich . ^[2] La interpretación de la misma como una distancia entre puntos en un espacio geométrico data de finales del siglo XIX y del desarrollo de geometrías no euclidianas . Cabe destacar que apareció en 1910 en las obras de Frigyes Riesz y Hermann Minkowski . La formalización de los espacios L ^p , que incluyen la geometría del taxi como un caso especial, se le atribuye a Riesz. ^[3] Al desarrollar la geometría de los números , Hermann Minkowski estableció su desigualdad de Minkowski , afirmando que estos espacios definen espacios vectoriales normados . ^[4]

El nombre de geometría de taxi fue introducido por Karl Menger en un folleto de 1952 titulado "Te gustará la geometría" , que acompañaba una exposición de geometría destinada al público general en el Museo de Ciencia e Industria de Chicago. ^[5]

Pensada como una estructura adicional en capas sobre el espacio euclidiano , la distancia del taxi depende de la orientación del sistema de coordenadas y se modifica por la rotación euclidiana del espacio, pero no se ve afectada por la traslación o las reflexiones alineadas con el eje . La geometría del taxi satisface todos los axiomas de Hilbert (una formalización de la geometría euclidiana ) excepto que la congruencia de los ángulos no se puede definir para que coincida exactamente con el concepto euclidiano, y bajo definiciones plausibles de ángulos congruentes del taxi, el axioma lado-ángulo-lado no se satisface ya que en general los triángulos con dos lados congruentes del taxi y un ángulo congruente del taxi entre ellos no son triángulos congruentes .

En cualquier espacio métrico , una esfera es un conjunto de puntos a una distancia fija, el radio , de un punto central específico. Mientras que una esfera euclidiana es redonda y rotacionalmente simétrica, bajo la distancia del taxi, la forma de una esfera es un politopo cruzado , la generalización n -dimensional de un octaedro regular , cuyos puntos satisfacen la ecuación:${\displaystyle \mathbf {p}}$

${\displaystyle d_{\text{T}}(\mathbf {p} ,\mathbf {c} )=\sum _{i=1}^{n}|p_{i}-c_{i}|=r,}$

donde es el centro y r es el radio. Los puntos de la esfera unitaria , una esfera de radio 1 centrada en el origen , satisfacen la ecuación${\displaystyle \mathbf {c}}$${\displaystyle \mathbf {p}}$${\textstyle d_{\text{T}}(\mathbf {p} ,\mathbf {0} )=\sum _ {i=1}^{n}|p_{i}|=1.}$

En la geometría bidimensional del taxi, la esfera (llamada círculo ) es un cuadrado orientado diagonalmente a los ejes de coordenadas. La imagen de la derecha muestra en rojo el conjunto de todos los puntos de una cuadrícula cuadrada con una distancia fija desde el centro azul. A medida que la cuadrícula se hace más fina, los puntos rojos se vuelven más numerosos y en el límite tienden a un cuadrado inclinado continuo. Cada lado tiene una longitud de taxi de 2 r , por lo que la circunferencia es de 8 r . Por lo tanto, en la geometría del taxi, el valor del análogo de la constante del círculo π , la relación entre la circunferencia y el diámetro , es igual a 4.

Una bola cerrada (o un disco cerrado en el caso bidimensional) es una esfera llena, el conjunto de puntos a una distancia menor o igual al radio de un centro específico. Para los autómatas celulares en una cuadrícula cuadrada, un disco de taxi es el entorno de von Neumann del rango r de su centro.

Un círculo de radio r para la distancia de Chebyshev ( métrica L _∞ ) en un plano también es un cuadrado con una longitud de lado 2 r paralelo a los ejes de coordenadas, por lo que la distancia de Chebyshev plana puede considerarse equivalente por rotación y escala a la distancia de taxi plana. Sin embargo, esta equivalencia entre las métricas L ₁ y L _∞ no se generaliza a dimensiones superiores.

Siempre que cada par en una colección de estos círculos tiene una intersección no vacía, existe un punto de intersección para toda la colección; por lo tanto, la distancia de Manhattan forma un espacio métrico inyectivo .

Sea una función continuamente diferenciable . Sea la longitud del arco de taxi del gráfico de en algún intervalo . Tome una partición del intervalo en subintervalos infinitesimales iguales y sea la longitud del arco de taxi del subarco. Entonces ^[6]${\displaystyle y=f(x)}$${\estilo de visualización s}$${\estilo de visualización f}$${\estilo de visualización [a,b]}$${\displaystyle \Delta s_{i}}$${\displaystyle i^{\text{th}}}$

$${\displaystyle \Delta s_{i}=\Delta x_{i}+\Delta y_{i}=\Delta x_{i}+|f(x_{i})-f(x_{i-1})|.}$$

Por el teorema del valor medio , existe algún punto entre y tal que . ^[7] Entonces la ecuación anterior puede escribirse$estilo de visualización x_{i}^{*}}$$Estilo de visualización x_{i}}$$estilo de visualización x_{i-1}}$${\displaystyle f(x_{i})-f(x_{i-1})=f'(x_{i}^{*})dx_{i}}$

$${\displaystyle \Delta s_{i}=\Delta x_{i}+|f'(x_{i}^{*})|\Delta x_{i}=\Delta x_{i}(1+|f'(x_{i}^{*})|).}$$

Luego se da como la suma de cada partición de a medida que se vuelven arbitrariamente pequeñas .${\estilo de visualización s}$${\estilo de visualización s}$${\estilo de visualización [a,b]}$

${\displaystyle {\begin{aligned}s&=\lim _{n\rightarrow \infty }\sum _{i=1}^{n}\Delta x_{i}(1+|f'(x_{i}^{*})|)\\&=\int _{a}^{b}1+|f'(x)|\,dx\end{aligned}}}$

Para comprobarlo, tomemos el círculo del taxi cuyo radio está centrado en el origen. Su curva en el primer cuadrante está dada por cuya longitud es${\estilo de visualización r}$${\displaystyle f(x)=-x+r}$

$${\displaystyle s=\int _{0}^{r}1+|-1|dx=2r}$$

Al multiplicar este valor por para tener en cuenta los cuadrantes restantes se obtiene , que coincide con la circunferencia de un círculo de taxi. ^[8] Ahora tomemos el círculo euclidiano de radio centrado en el origen, que está dado por . Su longitud de arco en el primer cuadrante está dada por${\estilo de visualización 4}$${\estilo de visualización 8r}$${\estilo de visualización r}$${\displaystyle f(x)={\sqrt {r^{2}-x^{2}}}}$

$${\displaystyle {\begin{aligned}s&=\int _{0}^{r}1+|{\frac {-x}{\sqrt {r^{2}-x^{2}}}}|dx\\&=x+{\sqrt {r^{2}-x^{2}}}{\bigg |}_{0}^{r}\\&=r-(-r)\\&=2r\end{aligned}}}$$

Teniendo en cuenta los cuadrantes restantes se obtiene nuevamente. Por lo tanto, la circunferencia del círculo del taxi y el círculo euclidiano en la métrica del taxi son iguales. ^[9] De hecho, para cualquier función que sea monótona y diferenciable con una derivada continua en un intervalo , la longitud del arco de sobre es . ^[10]${\displaystyle 4\times 2r=8r}$${\estilo de visualización f}$${\estilo de visualización [a,b]}$${\estilo de visualización f}$${\estilo de visualización [a,b]}$${\displaystyle (b-a)+\mid f(b)-f(a)\mid }$

Dos triángulos son congruentes si y solo si tres lados correspondientes son iguales en distancia y tres ángulos correspondientes son iguales en medida. Existen varios teoremas que garantizan la congruencia de triángulos en geometría euclidiana, a saber, ángulo-ángulo-lado (AAL), ángulo-lado-ángulo (AAL), lado-ángulo-lado (LAA) y lado-lado-lado (LAS). Sin embargo, en geometría de taxis, solo el LAAS garantiza la congruencia de triángulos. ^[11]

Tomemos, por ejemplo, dos triángulos rectángulos isósceles de taxi cuyos ángulos miden 45-90-45. Los dos catetos de ambos triángulos tienen una longitud de taxi de 2, pero las hipotenusas no son congruentes. Este contraejemplo elimina AAS, ASA y SAS. También elimina AASS, AAAS e incluso ASASA. Tener tres ángulos congruentes y dos lados no garantiza la congruencia de triángulos en la geometría del taxi. Por lo tanto, el único teorema de congruencia de triángulos en la geometría del taxi es SASAS, donde los tres lados correspondientes deben ser congruentes y al menos dos ángulos correspondientes deben ser congruentes. ^[12] Este resultado se debe principalmente al hecho de que la longitud de un segmento de línea depende de su orientación en la geometría del taxi.

Al resolver un sistema subdeterminado de ecuaciones lineales, el término de regularización para el vector de parámetros se expresa en términos de la norma (geometría del taxi) del vector. ^[13] Este enfoque aparece en el marco de recuperación de señales llamado detección comprimida .${\displaystyle \ell _{1}}$

La geometría del taxi puede utilizarse para evaluar las diferencias en las distribuciones de frecuencia discretas. Por ejemplo, en el empalme de ARN , las distribuciones posicionales de los hexámeros , que representan gráficamente la probabilidad de que cada hexámero aparezca en cada nucleótido dado cerca de un sitio de empalme, pueden compararse con la distancia L1. Cada distribución de posición puede representarse como un vector donde cada entrada representa la probabilidad de que el hexámero comience en un nucleótido determinado. Una gran distancia L1 entre los dos vectores indica una diferencia significativa en la naturaleza de las distribuciones, mientras que una distancia pequeña denota distribuciones de forma similar. Esto es equivalente a medir el área entre las dos curvas de distribución porque el área de cada segmento es la diferencia absoluta entre las probabilidades de las dos curvas en ese punto. Cuando se suman todos los segmentos, proporciona la misma medida que la distancia L1. ^[14]

• Distancia de Chebyshev
• Distancia de Hamming : la cantidad de bits que difieren entre dos cadenas de dígitos binarios
• Distancia de sotavento
• Envoltura convexa ortogonal  : superconjunto mínimo que interseca cada línea paralela al eje en un intervalo
• Paradoja de la escalera : La paradoja de que el límite de las longitudes de "curvas de escalera" cada vez más finas no tiende a la longitud del segmento de línea diagonal hacia el que tienden las curvas.

• Taxi métrico con semáforos

• Gardner, Martin (1997). "10. Geometría del taxi". Las últimas recreaciones . Copérnico. pp. 159–176. ISBN 0-387-94929-1.
• Krause, Eugene F. (1975). Geometría del taxi . Addison-Wesley. ISBN 0201039346.Reimpreso por Dover (1986), ISBN 0-486-25202-7 . 

• Weisstein, Eric W. "Taxicab Metric". MathWorld .
• Malkevitch, Joe (1 de octubre de 2007). "Taxi!". American Mathematical Society . Consultado el 6 de octubre de 2019 .