Diagrama de estados

Un diagrama de estados se utiliza en informática y campos relacionados para describir el comportamiento de los sistemas. Los diagramas de estados requieren que el sistema esté compuesto por un número finito de estados . A veces, esto es así, mientras que en otras ocasiones es una abstracción razonable . Existen muchas formas de diagramas de estados, que difieren ligeramente y tienen una semántica diferente .

Los diagramas de estados proporcionan una descripción abstracta del comportamiento de un sistema . Este comportamiento se analiza y representa mediante una serie de eventos que pueden ocurrir en uno o más estados posibles. De esta manera, "cada diagrama suele representar objetos de una sola clase y hace un seguimiento de los diferentes estados de sus objetos a través del sistema". ^[1]

Los diagramas de estados se pueden utilizar para representar gráficamente máquinas de estados finitos (también llamadas autómatas finitos). Esto fue introducido por Claude Shannon y Warren Weaver en su libro de 1949 The Mathematical Theory of Communication . Otra fuente es Taylor Booth en su libro de 1967 Sequential Machines and Automata Theory . Otra posible representación es la tabla de transición de estados .

Una forma clásica de diagrama de estados para un autómata finito (AF) es un gráfico dirigido con los siguientes elementos (Q, Σ, Z, δ, q ₀ , F): ^{[2] [3]}

• Vértices Q : un conjunto finito de estados, normalmente representados por círculos y etiquetados con símbolos designadores únicos o palabras escritas dentro de ellos.
• Símbolos de entrada Σ : una colección finita de símbolos de entrada o designadores
• Símbolos de salida Z : una colección finita de símbolos o designadores de salida

La función de salida ω representa el mapeo de pares ordenados de símbolos y estados de entrada a símbolos de salida, denotados matemáticamente como ω  : Σ × Q → Z .

• Aristas δ : representan transiciones de un estado a otro causadas por la entrada (identificadas por sus símbolos dibujados en las aristas). Una arista generalmente se dibuja como una flecha dirigida desde el estado actual al siguiente estado. Esta asignación describe la transición de estado causada por una entrada. Esto se escribe matemáticamente como δ  : Q × Σ → Q , por lo que δ (la función de transición) en la definición de la AF está dada tanto por el par de vértices conectados por una arista como por el símbolo en una arista en un diagrama que representa esta AF. El elemento δ(q, a) = p en la definición de la AF significa que desde el estado llamado q bajo el símbolo de entrada a , la transición al estado p ocurre en esta máquina. En el diagrama que representa esta AF, esto está representado por una arista etiquetada por a que apunta desde el vértice etiquetado por q al vértice etiquetado por p .
• Estado inicial q ₀ : (no se muestra en los ejemplos siguientes). El estado inicial q ₀ ∈ Q suele representarse mediante una flecha sin origen que apunte al estado. En textos más antiguos, ^{[2] [4]} el estado inicial no se muestra y debe inferirse del texto.
• Estado(s) de aceptación F : Si se utiliza, por ejemplo, para autómatas de aceptación, F ∈ Q es el estado de aceptación . Normalmente se dibuja como un círculo doble. A veces, el(los) estado(s) de aceptación funcionan como estados "finales" (detención, atrapados). [ ^3]

En el caso de un autómata finito determinista (DFA), un autómata finito no determinista (NFA), un autómata finito no determinista generalizado (GNFA) o una máquina de Moore , la entrada se indica en cada borde. En el caso de una máquina de Mealy , la entrada y la salida se indican en cada borde, separadas por una barra "/": "1/0" indica el cambio de estado al encontrarse con el símbolo "1", lo que hace que se muestre el símbolo "0". En el caso de una máquina de Moore, la salida del estado suele escribirse dentro del círculo del estado, también separada del designador del estado por una barra "/". También existen variantes que combinan estas dos notaciones.

Por ejemplo, si un estado tiene una serie de salidas (p. ej., "a= motor en sentido antihorario=1, b= luz de precaución inactiva=0"), el diagrama debería reflejar esto: p. ej., "q5/1,0" designa el estado q5 con salidas a=1, b=0. Este designador se escribirá dentro del círculo del estado.

S ₁ y S ₂ son estados y S ₁ es un estado de aceptación o un estado final . Cada arista está etiquetada con la entrada. Este ejemplo muestra un aceptor para números binarios que contienen un número par de ceros.

S ₀ , S ₁ y S ₂ son estados. Cada borde está etiquetado con " j / k ", donde j es la entrada y k es la salida.

Los diagramas de estados de Harel, ^[5] inventados por el científico informático David Harel , están ganando un uso generalizado desde que una variante se convirtió en parte del Lenguaje de modelado unificado (UML). ^{[ se necesita una fuente no primaria ]} El tipo de diagrama permite el modelado de superestados , regiones ortogonales y actividades como parte de un estado.

Los diagramas de estado clásicos requieren la creación de nodos distintos para cada combinación válida de parámetros que definen el estado. Para todos los sistemas, excepto los más simples, esto puede conducir a una gran cantidad de nodos y transiciones entre nodos ( explosión de estados y transiciones ), lo que reduce la legibilidad del diagrama de estado. Con los diagramas de estado de Harel es posible modelar múltiples diagramas de estado multifuncionales dentro del diagrama de estado. Cada una de estas máquinas de estado multifuncionales puede realizar transiciones internas sin afectar a las otras máquinas de estado. El estado actual de cada máquina de estado multifuncional define el estado del sistema. El diagrama de estado de Harel es equivalente a un diagrama de estado, pero mejora su legibilidad.

Existen otros conjuntos de semánticas disponibles para representar diagramas de estados. Por ejemplo, existen herramientas para modelar y diseñar lógica para controladores embebidos. ^[6] Estos diagramas, al igual que las máquinas de estados originales de Harel, ^[7] admiten estados anidados jerárquicamente, regiones ortogonales, acciones de estado y acciones de transición. ^[8]

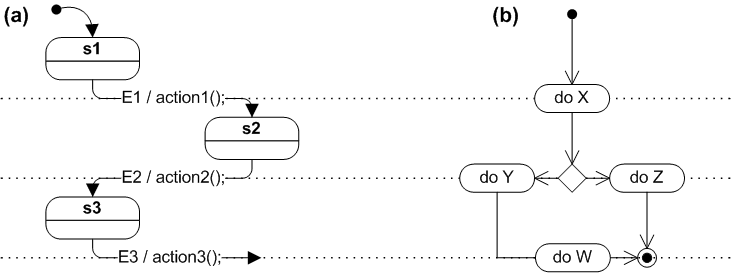
Los recién llegados al formalismo de la máquina de estados a menudo confunden los diagramas de estados con los diagramas de flujo . La figura siguiente muestra una comparación de un diagrama de estados con un diagrama de flujo. Una máquina de estados (panel (a)) realiza acciones en respuesta a eventos explícitos. En cambio, el diagrama de flujo (panel (b)) pasa automáticamente de un nodo a otro al completarse las actividades. ^[9]

Los nodos de los diagramas de flujo son aristas en el gráfico inducido de estados. La razón es que cada nodo de un diagrama de flujo representa un comando de programa. Un comando de programa es una acción que se debe ejecutar. Un comando no es un estado, pero cuando se aplica al estado del programa, provoca una transición a otro estado.

En más detalle, el código fuente representa un gráfico de programa. La ejecución del gráfico de programa (análisis e interpretación) da como resultado un gráfico de estado. Por lo tanto, cada gráfico de programa induce un gráfico de estado. La conversión del gráfico de programa a su gráfico de estado asociado se denomina "desdoblamiento" del gráfico de programa.

El gráfico del programa es una secuencia de comandos. Si no existen variables, el estado consiste únicamente en el contador del programa, que lleva un registro de la ubicación del programa durante la ejecución (cuál es el siguiente comando que se aplicará).

Antes de ejecutar un comando, el contador del programa se encuentra en una posición determinada (estado anterior a la ejecución del comando). Al ejecutar el comando, el contador del programa se desplaza al siguiente comando. Como el contador del programa es el estado completo, al ejecutar el comando se cambia el estado. Por lo tanto, el comando en sí corresponde a una transición entre los dos estados.

Ahora, consideremos el caso completo, cuando las variables existen y se ven afectadas por los comandos del programa que se están ejecutando. No solo cambia el contador del programa entre diferentes ubicaciones del contador del programa, sino que las variables también pueden cambiar de valor debido a los comandos ejecutados. En consecuencia, incluso si volvemos a revisar algún comando del programa (por ejemplo, en un bucle), esto no implica que el programa esté en el mismo estado.

En el caso anterior, el programa estaría en el mismo estado porque todo el estado es sólo el contador del programa. Por lo tanto, si el programa apunta a la misma posición (próximo comando) basta con especificar que estamos en el mismo estado. Sin embargo, si el estado incluye variables que cambian de valor, podemos estar en la misma posición del programa con valores de variable diferentes, es decir, en un estado diferente en el espacio de estados del programa. El término "desdoblamiento" se origina de esta multiplicación de posiciones al producir el gráfico de estados a partir del gráfico del programa.

Una autotransición es una transición donde el estado inicial y el final son el mismo.

Un ejemplo representativo es un bucle do que incrementa un contador hasta que se desborda y vuelve a ser 0. Aunque el bucle do ejecuta el mismo comando de incremento de forma iterativa, su espacio de estado no es un ciclo sino una línea. Esto resulta de que el estado es la ubicación del programa (aquí en ciclo) combinado con el valor del contador, que aumenta estrictamente (hasta el desbordamiento). Por lo tanto, se visitan diferentes estados en secuencia hasta que se produce el desbordamiento. Después del desbordamiento, el contador vuelve a ser 0, por lo que se vuelve a visitar el estado inicial en el espacio de estado, cerrando un ciclo en el espacio de estado (suponiendo que el contador se inicializó a 0).

La figura anterior intenta mostrar esa inversión de roles alineando los arcos de los diagramas de estados con las etapas de procesamiento del diagrama de flujo.

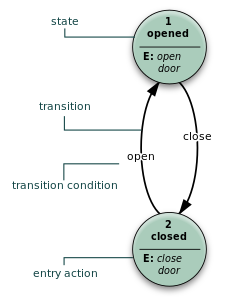
Se puede comparar un diagrama de flujo con una línea de montaje en una fábrica, ya que el diagrama de flujo describe la progresión de una tarea desde el principio hasta el final (por ejemplo, la transformación de la entrada de código fuente en la salida de código objeto por parte de un compilador). Una máquina de estados generalmente no tiene noción de dicha progresión. El ejemplo de la máquina de estados de la puerta que se muestra arriba no está en una etapa más avanzada en el estado "cerrado" que en el estado "abierto". Más bien, simplemente reacciona de manera diferente a los eventos de apertura/cierre. Un estado en una máquina de estados es una forma eficiente de especificar un comportamiento, en lugar de una etapa de procesamiento.

Una extensión interesante es permitir que los arcos fluyan desde cualquier número de estados a cualquier número de estados. Esto solo tiene sentido si se permite que el sistema esté en múltiples estados a la vez, lo que implica que un estado individual solo describe una condición u otro aspecto parcial del estado global general. El formalismo resultante se conoce como red de Petri .

Otra extensión permite la integración de diagramas de flujo dentro de los diagramas de estado de Harel. Esta extensión respalda el desarrollo de software que funciona tanto con eventos como con flujos de trabajo.

• David Harel
• DRAKÓN
• SCXML es un lenguaje XML que proporciona un entorno de ejecución genérico basado en máquinas de estados basado en diagramas de estados de Harel.
• Máquina de estados UML
• YAKINDU Statechart Tools es un software para modelar diagramas de estados (diagramas de estados de Harel, máquinas de Mealy, máquinas de Moore), simulación y generación de código fuente.

Wikimedia Commons tiene medios relacionados con Diagramas de estados .

• Introducción a los diagramas de máquinas de estados UML 2 por Scott W. Ambler
• Pautas para diagramas de máquinas de estados UML 2 de Scott W. Ambler
• Intelliwizard - UML StateWizard: un marco y una herramienta de desarrollo/modelado UML dinámico de ida y vuelta discontinuados que se ejecutaban en IDE populares bajo una licencia de código abierto.
• YAKINDU Statechart Tools: una herramienta de código abierto para la especificación y el desarrollo de sistemas reactivos basados ​​en eventos con la ayuda de máquinas de estados .
• Comprensión y uso de máquinas de estados Charlas técnicas de MATLAB sobre máquinas de estados
• FSM: Generación de máquinas de estados finitos de código abierto en Java por Alexander Sakharov FSM
• scxmlcc Una eficiente máquina de estados scxml para el compilador de C++.
• SMC: Un compilador de máquina de estados de código abierto que genera FSM para muchos lenguajes como C, Python, Lua, Scala, PHP, Java, VB, etc. SMC