Desplazamiento al rojo
| Relatividad general |
|---|
 |
| Part of a series on |
| Physical cosmology |
|---|
 |
| Special relativity |
|---|
 |
En física , un corrimiento al rojo es un aumento en la longitud de onda y una disminución correspondiente en la frecuencia y la energía de los fotones de la radiación electromagnética (como la luz ). El cambio opuesto, una disminución en la longitud de onda y un aumento en la frecuencia y la energía, se conoce como corrimiento al azul o corrimiento al rojo negativo. Los términos derivan de los colores rojo y azul que forman los extremos del espectro de luz visible . Las principales causas del corrimiento al rojo electromagnético en astronomía y cosmología son los movimientos relativos de las fuentes de radiación, que dan lugar al efecto Doppler relativista , y los potenciales gravitacionales, que desplazan al rojo gravitacionalmente la radiación que escapa. Todas las fuentes de luz suficientemente distantes muestran un corrimiento al rojo cosmológico correspondiente a velocidades de recesión proporcionales a sus distancias de la Tierra, un hecho conocido como la ley de Hubble que implica que el universo se está expandiendo .
Todos los corrimientos al rojo pueden entenderse bajo el paraguas de las leyes de transformación del marco . Las ondas gravitacionales , que también viajan a la velocidad de la luz , están sujetas a los mismos fenómenos de corrimiento al rojo. [1] El valor de un corrimiento al rojo a menudo se denota por la letra z , que corresponde al cambio fraccionario en la longitud de onda (positiva para corrimientos al rojo, negativa para corrimientos al azul), y por la relación de longitudes de onda 1 + z (que es mayor que 1 para corrimientos al rojo y menor que 1 para corrimientos al azul).
Ejemplos de un fuerte corrimiento al rojo son un rayo gamma percibido como un rayo X o una luz inicialmente visible percibida como ondas de radio . Se observan corrimientos al rojo más sutiles en las observaciones espectroscópicas de objetos astronómicos y se utilizan en tecnologías terrestres como el radar Doppler y los cañones de radar .
Existen otros procesos físicos que pueden provocar un cambio en la frecuencia de la radiación electromagnética, incluidos la dispersión y los efectos ópticos ; sin embargo, los cambios resultantes se pueden distinguir del corrimiento al rojo (astronómico) y generalmente no se los denomina como tales (véase la sección sobre óptica física y transferencia radiativa).
Historia
La historia de este fenómeno comenzó en el siglo XIX, con el desarrollo de la mecánica ondulatoria clásica y la exploración de los fenómenos asociados al efecto Doppler . El efecto recibe su nombre del matemático austríaco Christian Doppler , quien ofreció la primera explicación física conocida para el fenómeno en 1842. [2] En 1845, el científico holandés Christophorus Buys Ballot probó y confirmó la hipótesis para las ondas sonoras . [3] Doppler predijo correctamente que el fenómeno se aplicaría a todas las ondas y, en particular, sugirió que los colores variables de las estrellas podrían atribuirse a su movimiento con respecto a la Tierra. [4] Antes de que esto se verificara, se descubrió que los colores estelares se debían principalmente a la temperatura de una estrella , no al movimiento. Solo más tarde, Doppler fue reivindicado por observaciones verificadas del corrimiento al rojo. [ cita requerida ]
El corrimiento al rojo Doppler fue descrito por primera vez por el físico francés Hippolyte Fizeau en 1848, quien observó que el cambio en las líneas espectrales vistas en las estrellas se debía al efecto Doppler. El efecto a veces se denomina "efecto Doppler-Fizeau". En 1868, el astrónomo británico William Huggins fue el primero en determinar la velocidad de una estrella alejándose de la Tierra mediante este método. [5] En 1871, el corrimiento al rojo óptico se confirmó cuando el fenómeno se observó en las líneas de Fraunhofer , utilizando la rotación solar, aproximadamente 0,1 Å en el rojo. [6] En 1887, Vogel y Scheiner descubrieron el "efecto Doppler anual", el cambio anual en el corrimiento Doppler de las estrellas ubicadas cerca de la eclíptica, debido a la velocidad orbital de la Tierra. [7] En 1901, Aristarkh Belopolsky verificó el corrimiento al rojo óptico en el laboratorio utilizando un sistema de espejos giratorios. [8]
Arthur Eddington utilizó el término "corrimiento al rojo" ya en 1923, [9] [10] aunque la palabra no aparece sin guión hasta alrededor de 1934, cuando Willem de Sitter la utilizó. [11]
A partir de sus observaciones en 1912, Vesto Slipher descubrió que la mayoría de las galaxias espirales , que en aquel entonces se consideraban principalmente nebulosas espirales , presentaban desplazamientos al rojo considerables. Slipher informó por primera vez sobre su medición en el volumen inaugural del Boletín del Observatorio Lowell . [12] Tres años después, escribió una reseña en la revista Popular Astronomy . [13] En ella, afirmaba que "el descubrimiento temprano de que la gran espiral de Andrómeda tenía la excepcional velocidad de -300 km(/s) mostró los medios disponibles en ese momento, capaces de investigar no solo los espectros de las espirales sino también sus velocidades". [14]
Slipher informó las velocidades de 15 nebulosas espirales distribuidas por toda la esfera celeste , todas menos tres con velocidades "positivas" (es decir, recesivas) observables. Posteriormente, Edwin Hubble descubrió una relación aproximada entre los desplazamientos al rojo de dichas "nebulosas" y las distancias a ellas, con la formulación de su epónima ley de Hubble . [15] Milton Humason trabajó en esas observaciones con Hubble. [16] Estas observaciones corroboraron el trabajo de Alexander Friedmann de 1922, en el que derivó las ecuaciones de Friedmann-Lemaître . [17] Ahora se consideran una prueba sólida de un universo en expansión y de la teoría del Big Bang . [18]
Medición, caracterización e interpretación

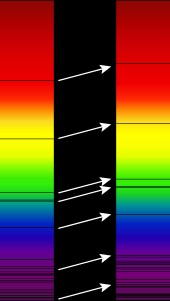
El espectro de luz que proviene de una fuente (ver la ilustración del espectro idealizado en la parte superior derecha) se puede medir. Para determinar el corrimiento al rojo, se buscan características en el espectro, como líneas de absorción , líneas de emisión u otras variaciones en la intensidad de la luz. Si se encuentran, estas características se pueden comparar con características conocidas en el espectro de varios compuestos químicos encontrados en experimentos donde ese compuesto se encuentra en la Tierra. Un elemento atómico muy común en el espacio es el hidrógeno .
El espectro de luz que originalmente no tenía características y que atravesó el hidrógeno mostrará un espectro característico específico del hidrógeno que tiene características a intervalos regulares. Si se limita a las líneas de absorción, se vería similar a la ilustración (arriba a la derecha). Si se ve el mismo patrón de intervalos en un espectro observado de una fuente distante, pero que ocurre en longitudes de onda desplazadas, también se puede identificar como hidrógeno. Si se identifica la misma línea espectral en ambos espectros, pero en longitudes de onda diferentes, entonces se puede calcular el corrimiento al rojo utilizando la tabla siguiente.
Para determinar el corrimiento al rojo de un objeto de esta manera se requiere un rango de frecuencias o longitudes de onda. Para calcular el corrimiento al rojo, se debe conocer la longitud de onda de la luz emitida en el marco de reposo de la fuente: en otras palabras, la longitud de onda que mediría un observador ubicado adyacente a la fuente y en movimiento con ella. Dado que en aplicaciones astronómicas esta medición no se puede realizar directamente, porque eso requeriría viajar a la estrella distante de interés, se utiliza en su lugar el método que utiliza líneas espectrales descrito aquí. Los corrimientos al rojo no se pueden calcular observando características no identificadas cuya frecuencia en el marco de reposo se desconoce, o con un espectro sin características o ruido blanco (fluctuaciones aleatorias en un espectro). [20]
El corrimiento al rojo (y al azul) se puede caracterizar por la diferencia relativa entre las longitudes de onda (o frecuencias) observadas y emitidas de un objeto. En astronomía, es habitual referirse a este cambio utilizando una cantidad adimensional llamada z . Si λ representa la longitud de onda y f representa la frecuencia (nótese que λf = c donde c es la velocidad de la luz ), entonces z se define mediante las ecuaciones: [21]
| Basado en la longitud de onda | Basado en la frecuencia |
|---|---|
Después de medir z , la distinción entre corrimiento al rojo y corrimiento al azul es simplemente una cuestión de si z es positivo o negativo. Por ejemplo, los corrimientos al azul por efecto Doppler ( z < 0 ) están asociados con objetos que se acercan (se acercan) al observador con la luz desplazándose a energías mayores . Por el contrario, los corrimientos al rojo por efecto Doppler ( z > 0 ) están asociados con objetos que se alejan (se alejan) del observador con la luz desplazándose a energías más bajas. Del mismo modo, los corrimientos al azul gravitacionales están asociados con la luz emitida desde una fuente que reside dentro de un campo gravitacional más débil como se observa desde dentro de un campo gravitacional más fuerte, mientras que el corrimiento al rojo gravitacional implica las condiciones opuestas.
Fórmulas de corrimiento al rojo
En la relatividad general se pueden derivar varias fórmulas importantes para casos especiales de corrimiento al rojo en ciertas geometrías especiales del espacio-tiempo, como se resume en la siguiente tabla. En todos los casos, la magnitud del corrimiento (el valor de z ) es independiente de la longitud de onda. [22]
| Tipo de corrimiento al rojo | Geometría | Fórmula [23] |
|---|---|---|
| Doppler relativista | Espacio de Minkowski (espacio-tiempo plano) | Para movimiento completamente en
|
| Desplazamiento al rojo cosmológico | Espacio-tiempo FLRW (universo del Big Bang en expansión) |
|
| Desplazamiento al rojo gravitacional | cualquier espacio-tiempo estacionario | Para la geometría de Schwarzschild :
En términos de velocidad de escape : para |
Efecto Doppler
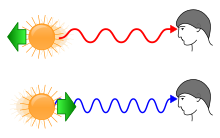
Si una fuente de luz se aleja de un observador, se produce un corrimiento al rojo ( z > 0 ); si la fuente se acerca al observador, se produce un corrimiento al azul ( z < 0 ). Esto es cierto para todas las ondas electromagnéticas y se explica por el efecto Doppler . En consecuencia, este tipo de corrimiento al rojo se denomina corrimiento al rojo Doppler . Si la fuente se aleja del observador con una velocidad v , que es mucho menor que la velocidad de la luz ( v ≪ c ), el corrimiento al rojo viene dado por
- (desde )
donde c es la velocidad de la luz . En el efecto Doppler clásico, la frecuencia de la fuente no se modifica, pero el movimiento de recesión provoca la ilusión de una frecuencia más baja.
Un tratamiento más completo del corrimiento al rojo Doppler requiere considerar los efectos relativistas asociados con el movimiento de fuentes cercanas a la velocidad de la luz. Una derivación completa del efecto se puede encontrar en el artículo sobre el efecto Doppler relativista . En resumen, los objetos que se mueven cerca de la velocidad de la luz experimentarán desviaciones de la fórmula anterior debido a la dilatación del tiempo de la relatividad especial , que se puede corregir introduciendo el factor de Lorentz γ en la fórmula Doppler clásica de la siguiente manera (para el movimiento únicamente en la línea de visión):
Este fenómeno se observó por primera vez en un experimento de 1938 realizado por Herbert E. Ives y GR Stilwell, llamado experimento Ives-Stilwell . [24]
Como el factor de Lorentz depende únicamente de la magnitud de la velocidad, esto hace que el corrimiento al rojo asociado con la corrección relativista sea independiente de la orientación del movimiento de la fuente. En cambio, la parte clásica de la fórmula depende de la proyección del movimiento de la fuente en la línea de visión , lo que produce resultados diferentes para distintas orientaciones. Si θ es el ángulo entre la dirección del movimiento relativo y la dirección de emisión en el marco del observador [25] (el ángulo cero es directamente en dirección opuesta al observador), la forma completa del efecto Doppler relativista se convierte en:
y para el movimiento únicamente en la línea de visión ( θ = 0° ), esta ecuación se reduce a:
Para el caso especial de que la luz se mueve en ángulo recto ( θ = 90° ) con respecto a la dirección del movimiento relativo en el marco del observador, [26] el corrimiento al rojo relativista se conoce como corrimiento al rojo transversal , y un corrimiento al rojo:
se mide, aunque el objeto no se esté alejando del observador. Incluso cuando la fuente se está moviendo hacia el observador, si hay un componente transversal en el movimiento, entonces hay cierta velocidad a la cual la dilatación simplemente cancela el desplazamiento hacia el azul esperado y a mayor velocidad la fuente que se acerca se desplazará hacia el rojo. [27]
Expansión del espacio
A principios del siglo XX, Slipher, Wirtz y otros realizaron las primeras mediciones de los corrimientos al rojo y al azul de las galaxias más allá de la Vía Láctea . Inicialmente interpretaron estos corrimientos al rojo y al azul como debidos a movimientos aleatorios, pero más tarde Lemaître (1927) y Hubble (1929), utilizando datos anteriores, descubrieron una correlación aproximadamente lineal entre los crecientes corrimientos al rojo de las galaxias y las distancias a las mismas. Lemaître se dio cuenta de que estas observaciones podían explicarse por un mecanismo de producción de corrimientos al rojo visto en las soluciones de Friedmann a las ecuaciones de la relatividad general de Einstein . La correlación entre los corrimientos al rojo y las distancias surge en todos los modelos en expansión. [18]
Este corrimiento al rojo cosmológico se suele atribuir al estiramiento de las longitudes de onda de los fotones que se propagan a través del espacio en expansión. Sin embargo, esta interpretación puede ser engañosa; el espacio en expansión es solo una elección de coordenadas y, por lo tanto, no puede tener consecuencias físicas. El corrimiento al rojo cosmológico se interpreta de manera más natural como un corrimiento Doppler que surge debido a la recesión de objetos distantes. [28]
Las consecuencias observacionales de este efecto pueden derivarse utilizando las ecuaciones de la relatividad general que describen un universo homogéneo e isótropo . El corrimiento al rojo cosmológico puede escribirse, por tanto, como una función de a , el factor de escala cósmico dependiente del tiempo :
En un universo en expansión como el que habitamos, el factor de escala aumenta monótonamente a medida que pasa el tiempo, por lo tanto, z es positivo y las galaxias distantes aparecen desplazadas al rojo.
Utilizando un modelo de expansión del universo, el corrimiento al rojo puede relacionarse con la edad de un objeto observado, la llamada relación tiempo cósmico -corrimiento al rojo. Denotemos una relación de densidad como Ω 0 :
donde ρ crit es la densidad crítica que delimita un universo que finalmente se desmorona de uno que simplemente se expande. Esta densidad es de unos tres átomos de hidrógeno por metro cúbico de espacio. [29] En grandes desplazamientos al rojo, 1 + z > Ω 0 −1 , se encuentra:
donde H 0 es la constante de Hubble actual y z es el corrimiento al rojo. [30] [31]
Hay varios sitios web para calcular distintos tiempos y distancias a partir del corrimiento al rojo, ya que los cálculos precisos requieren integrales numéricas para la mayoría de los valores de los parámetros. [32] [33] [34] [35]
Distinguir entre efectos cosmológicos y locales
Para corrimientos al rojo cosmológicos de z < 0,01, los corrimientos al rojo y al azul Doppler adicionales debidos a los movimientos peculiares de las galaxias entre sí causan una amplia dispersión de la Ley de Hubble estándar . [36] La situación resultante puede ilustrarse mediante el Universo en forma de lámina de goma en expansión , una analogía cosmológica común utilizada para describir la expansión del espacio. Si dos objetos están representados por cojinetes de bolas y el espacio-tiempo por una lámina de goma que se estira, el efecto Doppler se produce al hacer rodar las bolas a lo largo de la lámina para crear un movimiento peculiar. El corrimiento al rojo cosmológico ocurre cuando los cojinetes de bolas están pegados a la lámina y esta se estira. [37] [38] [39]
Los corrimientos al rojo de las galaxias incluyen tanto un componente relacionado con la velocidad de recesión debido a la expansión del universo como un componente relacionado con el movimiento peculiar (corrimiento Doppler). [40] El corrimiento al rojo debido a la expansión del universo depende de la velocidad de recesión de una manera determinada por el modelo cosmológico elegido para describir la expansión del universo, que es muy diferente de cómo el corrimiento al rojo Doppler depende de la velocidad local. [41] Al describir el origen de la expansión cosmológica del corrimiento al rojo, el cosmólogo Edward Robert Harrison dijo: "La luz sale de una galaxia, que está estacionaria en su región local del espacio, y finalmente es recibida por observadores que están estacionarios en su propia región local del espacio. Entre la galaxia y el observador, la luz viaja a través de vastas regiones de espacio en expansión. Como resultado, todas las longitudes de onda de la luz se estiran por la expansión del espacio. Es tan simple como eso..." [42] Steven Weinberg aclaró: "El aumento de la longitud de onda desde la emisión hasta la absorción de la luz no depende de la tasa de cambio de a ( t ) [aquí a ( t ) es el factor de escala de Robertson-Walker ] en los momentos de emisión o absorción, sino del aumento de a ( t ) en todo el período desde la emisión hasta la absorción". [43]
Si el universo se estuviera contrayendo en lugar de expandirse, veríamos galaxias distantes desplazadas hacia el azul en una cantidad proporcional a su distancia en lugar de desplazadas hacia el rojo. [44]
Desplazamiento al rojo gravitacional
En la teoría de la relatividad general , existe una dilatación del tiempo dentro de un pozo gravitacional. Esto se conoce como corrimiento al rojo gravitacional o corrimiento de Einstein . [45] La derivación teórica de este efecto se desprende de la solución de Schwarzschild de las ecuaciones de Einstein , que produce la siguiente fórmula para el corrimiento al rojo asociado con un fotón que viaja en el campo gravitacional de una masa no cargada , no rotatoria y esféricamente simétrica :
dónde
- G es la constante gravitacional ,
- M es la masa del objeto que crea el campo gravitacional,
- r es la coordenada radial de la fuente (que es análoga a la distancia clásica desde el centro del objeto, pero en realidad es una coordenada de Schwarzschild ), y
- c es la velocidad de la luz .
Este resultado del corrimiento al rojo gravitacional se puede derivar de los supuestos de la relatividad especial y del principio de equivalencia ; no se requiere la teoría completa de la relatividad general. [46]
El efecto es muy pequeño pero medible en la Tierra mediante el efecto Mössbauer y se observó por primera vez en el experimento Pound-Rebka . [47] Sin embargo, es significativo cerca de un agujero negro , y a medida que un objeto se acerca al horizonte de sucesos el corrimiento al rojo se vuelve infinito. También es la causa principal de grandes fluctuaciones de temperatura a escala angular en la radiación de fondo de microondas cósmica (véase el efecto Sachs-Wolfe ). [48]
Observaciones en astronomía
El corrimiento al rojo observado en astronomía se puede medir porque los espectros de emisión y absorción de los átomos son distintivos y bien conocidos, calibrados a partir de experimentos espectroscópicos en laboratorios en la Tierra. Cuando se mide el corrimiento al rojo de varias líneas de absorción y emisión de un único objeto astronómico, se descubre que z es notablemente constante. Aunque los objetos distantes pueden verse ligeramente borrosos y las líneas ensanchadas, esto no es más que lo que se puede explicar por el movimiento térmico o mecánico de la fuente. Por estas razones y otras, el consenso entre los astrónomos es que los corrimientos al rojo que observan se deben a alguna combinación de las tres formas establecidas de corrimientos al rojo de tipo Doppler. Las hipótesis y explicaciones alternativas para el corrimiento al rojo, como la luz cansada, no se consideran generalmente plausibles. [50]
La espectroscopia, como medida, es considerablemente más difícil que la fotometría simple , que mide el brillo de los objetos astronómicos a través de ciertos filtros . [51] Cuando los datos fotométricos son todo lo que está disponible (por ejemplo, el Campo Profundo del Hubble y el Campo Ultra Profundo del Hubble ), los astrónomos confían en una técnica para medir los desplazamientos al rojo fotométricos . [52] Debido a los amplios rangos de longitud de onda en los filtros fotométricos y las suposiciones necesarias sobre la naturaleza del espectro en la fuente de luz, los errores para este tipo de mediciones pueden llegar hasta δ z = 0,5 , y son mucho menos confiables que las determinaciones espectroscópicas. [53]
Sin embargo, la fotometría permite al menos una caracterización cualitativa de un corrimiento al rojo. Por ejemplo, si un espectro similar al del Sol tuviera un corrimiento al rojo de z = 1 , sería más brillante en el infrarrojo (1000 nm) en lugar de en el color azul-verde (500 nm) asociado con el pico de su espectro de cuerpo negro , y la intensidad de la luz se reducirá en el filtro por un factor de cuatro, (1 + z ) 2 . Tanto la tasa de conteo de fotones como la energía de los fotones están desplazadas al rojo. (Véase la corrección K para más detalles sobre las consecuencias fotométricas del corrimiento al rojo.) [54]
Observaciones locales
En los objetos cercanos (dentro de nuestra galaxia, la Vía Láctea ), los corrimientos al rojo observados casi siempre están relacionados con las velocidades de la línea de visión asociadas con los objetos que se observan. Las observaciones de dichos corrimientos al rojo y al azul han permitido a los astrónomos medir velocidades y parametrizar las masas de las estrellas en órbita en sistemas binarios espectroscópicos , un método empleado por primera vez en 1868 por el astrónomo británico William Huggins . [5] De manera similar, los pequeños corrimientos al rojo y al azul detectados en las mediciones espectroscópicas de estrellas individuales son una forma en que los astrónomos han podido diagnosticar y medir la presencia y las características de los sistemas planetarios alrededor de otras estrellas e incluso han realizado mediciones diferenciales muy detalladas de los corrimientos al rojo durante los tránsitos planetarios para determinar parámetros orbitales precisos. [55]
Las mediciones finamente detalladas de los corrimientos al rojo se utilizan en heliosismología para determinar los movimientos precisos de la fotosfera del Sol . [56] Los corrimientos al rojo también se han utilizado para realizar las primeras mediciones de las tasas de rotación de los planetas , [57] las velocidades de las nubes interestelares , [58] la rotación de las galaxias , [22] y la dinámica de la acreción en estrellas de neutrones y agujeros negros que exhiben corrimientos al rojo tanto Doppler como gravitacionales. [59] Las temperaturas de varios objetos emisores y absorbentes se pueden obtener midiendo el ensanchamiento Doppler , es decir, los corrimientos al rojo y al azul sobre una sola línea de emisión o absorción. [60] Al medir el ensanchamiento y los desplazamientos de la línea de hidrógeno de 21 centímetros en diferentes direcciones, los astrónomos han podido medir las velocidades de recesión del gas interestelar , lo que a su vez revela la curva de rotación de nuestra Vía Láctea. [22] Se han realizado mediciones similares en otras galaxias, como Andrómeda . [22] Como herramienta de diagnóstico, las mediciones de corrimiento al rojo son una de las mediciones espectroscópicas más importantes realizadas en astronomía.
Observaciones extragalácticas
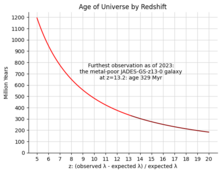
Los objetos más distantes presentan mayores corrimientos al rojo correspondientes al flujo de Hubble del universo . El corrimiento al rojo más grande observado, correspondiente a la mayor distancia y más atrás en el tiempo, es el de la radiación de fondo de microondas cósmica ; el valor numérico de su corrimiento al rojo es de aproximadamente z = 1089 ( z = 0 corresponde al tiempo presente), y muestra el estado del universo hace aproximadamente 13.800 millones de años, [61] y 379.000 años después de los momentos iniciales del Big Bang . [62]
Los núcleos puntuales luminosos de los cuásares fueron los primeros objetos de "alto corrimiento al rojo" ( z > 0,1 ) descubiertos antes de que la mejora de los telescopios permitiera el descubrimiento de otras galaxias de alto corrimiento al rojo. [ cita requerida ]
En el caso de galaxias más distantes que el Grupo Local y el cercano Cúmulo de Virgo , pero dentro de un radio de mil megaparsecs aproximadamente , el corrimiento al rojo es aproximadamente proporcional a la distancia de la galaxia. Esta correlación fue observada por primera vez por Edwin Hubble y se la conoce como la ley de Hubble . Vesto Slipher fue el primero en descubrir los corrimientos al rojo galácticos, alrededor de 1912, mientras que Hubble correlacionó las mediciones de Slipher con las distancias que midió por otros medios para formular su Ley. [63]
En el modelo cosmológico ampliamente aceptado basado en la relatividad general , el corrimiento al rojo es principalmente el resultado de la expansión del espacio: esto significa que cuanto más lejos está una galaxia de nosotros, más se ha expandido el espacio en el tiempo desde que la luz salió de esa galaxia, por lo que cuanto más se ha estirado la luz, más se desplaza al rojo y, por lo tanto, más rápido parece alejarse de nosotros. La ley de Hubble se deriva en parte del principio copernicano . [63] Debido a que generalmente no se sabe qué tan luminosos son los objetos, medir el corrimiento al rojo es más fácil que las mediciones de distancia más directas, por lo que el corrimiento al rojo a veces se convierte en la práctica en una medición de distancia cruda utilizando la ley de Hubble. [ cita requerida ]
Las interacciones gravitacionales de las galaxias entre sí y con los cúmulos causan una dispersión significativa en el gráfico normal del diagrama de Hubble. Las velocidades peculiares asociadas con las galaxias superponen un rastro aproximado de la masa de los objetos virializados en el universo. Este efecto conduce a fenómenos como galaxias cercanas (como la galaxia de Andrómeda ) que exhiben corrimientos al azul a medida que caemos hacia un baricentro común , y mapas de corrimientos al rojo de cúmulos que muestran un efecto de dedos de Dios debido a la dispersión de velocidades peculiares en una distribución aproximadamente esférica. [63] Este componente adicional brinda a los cosmólogos la oportunidad de medir las masas de los objetos independientemente de la relación masa-luz (la relación entre la masa de una galaxia en masas solares y su brillo en luminosidades solares), una herramienta importante para medir la materia oscura . [64] [ página necesaria ]
La relación lineal de la ley de Hubble entre la distancia y el corrimiento al rojo supone que la tasa de expansión del universo es constante. Sin embargo, cuando el universo era mucho más joven, la tasa de expansión, y por lo tanto la "constante" de Hubble, era mayor que la actual. Por lo tanto, para galaxias más distantes, cuya luz ha estado viajando hacia nosotros durante tiempos mucho más largos, la aproximación de la tasa de expansión constante falla, y la ley de Hubble se convierte en una relación integral no lineal y dependiente de la historia de la tasa de expansión desde la emisión de la luz de la galaxia en cuestión. Las observaciones de la relación corrimiento al rojo-distancia se pueden utilizar, entonces, para determinar la historia de la expansión del universo y, por lo tanto, el contenido de materia y energía. [ cita requerida ]
Aunque durante mucho tiempo se creyó que la tasa de expansión ha estado disminuyendo continuamente desde el Big Bang, las observaciones a partir de 1988 de la relación desplazamiento al rojo-distancia utilizando supernovas de tipo Ia han sugerido que en tiempos comparativamente recientes la tasa de expansión del universo ha comenzado a acelerarse . [65]
Los mayores desplazamientos al rojo

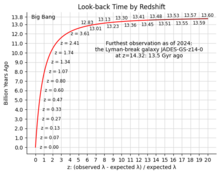
Actualmente, los objetos con los mayores corrimientos al rojo conocidos son las galaxias y los objetos que producen estallidos de rayos gamma. [ cita requerida ] Los corrimientos al rojo más fiables provienen de datos espectroscópicos , [ cita requerida ] y el corrimiento al rojo espectroscópico confirmado más alto de una galaxia es el de JADES-GS-z14-0 con un corrimiento al rojo de z = 14,32 , correspondiente a 290 millones de años después del Big Bang. [66] El récord anterior lo tenía GN-z11 , [67] con un corrimiento al rojo de z = 11,1 , correspondiente a 400 millones de años después del Big Bang, y UDFy-38135539 [68] con un corrimiento al rojo de z = 8,6 , correspondiente a 600 millones de años después del Big Bang.
Un poco menos fiables son los corrimientos al rojo de ruptura de Lyman , el más alto de los cuales es la galaxia con lente A1689-zD1 con un corrimiento al rojo z = 7,5 [69] [70] y el siguiente más alto es z = 7,0 . [71] El estallido de rayos gamma observado más distante con una medición de corrimiento al rojo espectroscópico fue GRB 090423 , que tuvo un corrimiento al rojo de z = 8,2 . [72] El cuásar conocido más distante, ULAS J1342+0928 , está en z = 7,54 . [73] [74] La radiogalaxia de corrimiento al rojo más alto conocida (TGSS1530) está en un corrimiento al rojo z = 5,72 [75] y el material molecular de corrimiento al rojo más alto conocido es la detección de la emisión de la molécula de CO del cuásar SDSS J1148+5251 en z = 6,42 . [76]
Los objetos extremadamente rojos (ERO) son fuentes astronómicas de radiación que irradian energía en la parte roja e infrarroja cercana del espectro electromagnético. Pueden ser galaxias con brotes de formación estelar que tienen un alto corrimiento al rojo acompañado de enrojecimiento por el polvo que se interpone, o podrían ser galaxias elípticas muy desplazadas al rojo con una población estelar más antigua (y por lo tanto más roja). [77] Los objetos que son incluso más rojos que los ERO se denominan objetos hiperextremadamente rojos (HERO). [78]
El fondo cósmico de microondas tiene un corrimiento al rojo de z = 1089 , que corresponde a una edad de aproximadamente 379.000 años después del Big Bang y una distancia propia de más de 46 mil millones de años luz. [79] La primera luz aún por observar de las estrellas más antiguas de la Población III , no mucho después de que se formaran los átomos por primera vez y el CMB dejara de ser absorbido casi por completo, puede tener corrimientos al rojo en el rango de 20 < z < 100. [ 80] Otros eventos de alto corrimiento al rojo predichos por la física pero que actualmente no son observables son el fondo cósmico de neutrinos de unos dos segundos después del Big Bang (y un corrimiento al rojo superior a z > 10 10 ) [81] y el fondo cósmico de ondas gravitacionales emitidas directamente por la inflación con un corrimiento al rojo superior a z > 10 25. [82 ]
En junio de 2015, los astrónomos informaron de la existencia de evidencias de estrellas de la Población III en la galaxia Cosmos Redshift 7 en z = 6,60 . Es probable que dichas estrellas hayan existido en el universo muy temprano (es decir, en un alto corrimiento al rojo) y que hayan iniciado la producción de elementos químicos más pesados que el hidrógeno que son necesarios para la posterior formación de planetas y la vida tal como la conocemos. [83] [84]
Estudios de corrimiento al rojo

Con la llegada de los telescopios automatizados y las mejoras en los espectroscopios , se han realizado varias colaboraciones para mapear el universo en el espacio de corrimiento al rojo. Al combinar el corrimiento al rojo con los datos de posición angular, un estudio de corrimiento al rojo mapea la distribución 3D de la materia dentro de un campo del cielo. Estas observaciones se utilizan para medir las propiedades de la estructura a gran escala del universo. La Gran Muralla , un vasto supercúmulo de galaxias de más de 500 millones de años luz de ancho, proporciona un ejemplo dramático de una estructura a gran escala que los estudios de corrimiento al rojo pueden detectar. [85]
El primer estudio de corrimiento al rojo fue el CfA Redshift Survey , iniciado en 1977 y cuya recopilación de datos inicial se completó en 1982. [ 86] Más recientemente, el 2dF Galaxy Redshift Survey determinó la estructura a gran escala de una sección del universo, midiendo los corrimientos al rojo de más de 220.000 galaxias; la recopilación de datos se completó en 2002 y el conjunto de datos final se publicó el 30 de junio de 2003. [87] El Sloan Digital Sky Survey (SDSS), que está en curso desde 2013, tiene como objetivo medir los corrimientos al rojo de alrededor de 3 millones de objetos. [88] El SDSS ha registrado corrimientos al rojo de galaxias de hasta 0,8 y ha participado en la detección de cuásares más allá de z = 6. El DEEP2 Redshift Survey utiliza los telescopios Keck con el nuevo espectrógrafo "DEIMOS" ; DEEP2, una continuación del programa piloto DEEP1, está diseñado para medir galaxias débiles con corrimientos al rojo de 0,7 y superiores, y por lo tanto está previsto que proporcione un complemento de alto corrimiento al rojo a SDSS y 2dF. [89]
Efectos de la óptica física o transferencia radiativa
Las interacciones y fenómenos resumidos en los temas de transferencia radiativa y óptica física pueden dar lugar a cambios en la longitud de onda y frecuencia de la radiación electromagnética. En tales casos, los cambios corresponden a una transferencia física de energía a la materia u otros fotones en lugar de ser una transformación entre marcos de referencia. Tales cambios pueden deberse a fenómenos físicos como efectos de coherencia o la dispersión de la radiación electromagnética , ya sea de partículas elementales cargadas , de partículas o de fluctuaciones del índice de refracción en un medio dieléctrico , como ocurre en el fenómeno de radio de los silbadores de radio . [22] Si bien a estos fenómenos a veces se los denomina "desplazamientos al rojo" y "desplazamientos al azul", en astrofísica las interacciones luz-materia que dan lugar a cambios de energía en el campo de radiación generalmente se denominan "enrojecimiento" en lugar de "desplazamiento al rojo", que, como término, normalmente se reserva para los efectos analizados anteriormente. [22]
En muchas circunstancias, la dispersión hace que la radiación se enrojezca porque la entropía da como resultado el predominio de muchos fotones de baja energía sobre unos pocos de alta energía (mientras se conserva la energía total ). [22] Excepto posiblemente bajo condiciones cuidadosamente controladas, la dispersión no produce el mismo cambio relativo en la longitud de onda en todo el espectro; es decir, cualquier z calculado es generalmente una función de la longitud de onda. Además, la dispersión de medios aleatorios generalmente ocurre en muchos ángulos , y z es una función del ángulo de dispersión. Si ocurre dispersión múltiple, o las partículas dispersantes tienen movimiento relativo, entonces generalmente también hay distorsión de las líneas espectrales . [22]
En la astronomía interestelar , los espectros visibles pueden aparecer más rojos debido a procesos de dispersión en un fenómeno conocido como enrojecimiento interestelar [22] —de manera similar, la dispersión de Rayleigh causa el enrojecimiento atmosférico del Sol que se ve en el amanecer o el atardecer y hace que el resto del cielo tenga un color azul. Este fenómeno es distinto del corrimiento al rojo porque las líneas espectroscópicas no se desplazan a otras longitudes de onda en los objetos enrojecidos y hay un oscurecimiento y una distorsión adicionales asociados con el fenómeno debido a que los fotones se dispersan dentro y fuera de la línea de visión . [ cita requerida ]
Desplazamiento al azul
El opuesto de un corrimiento al rojo es un corrimiento al azul . Un corrimiento al azul es cualquier disminución en la longitud de onda (aumento en la energía ), con un aumento correspondiente en la frecuencia, de una onda electromagnética . En la luz visible , esto desplaza un color hacia el extremo azul del espectro.
Desplazamiento al azul Doppler

El corrimiento al azul Doppler es causado por el movimiento de una fuente hacia el observador. El término se aplica a cualquier disminución en la longitud de onda y aumento en la frecuencia causados por el movimiento relativo, incluso fuera del espectro visible . Solo los objetos que se mueven a velocidades casi relativistas hacia el observador son notablemente más azules a simple vista , pero la longitud de onda de cualquier fotón reflejado o emitido u otra partícula se acorta en la dirección del viaje. [90]
El corrimiento al azul Doppler se utiliza en astronomía para determinar el movimiento relativo:
- La galaxia de Andrómeda se está moviendo hacia nuestra propia galaxia, la Vía Láctea , dentro del Grupo Local ; por lo tanto, cuando se observa desde la Tierra, su luz está experimentando un desplazamiento hacia el azul. [91]
- Los componentes de un sistema estelar binario se desplazarán hacia el azul cuando se acerquen a la Tierra
- Al observar galaxias espirales, el lado que gira hacia nosotros tendrá un ligero desplazamiento hacia el azul en relación con el lado que gira en dirección opuesta a nosotros (ver relación de Tully-Fisher ).
- Se sabe que los blazares impulsan chorros relativistas hacia nosotros, emitiendo radiación de sincrotrón y radiación de frenado que parece desplazada hacia el azul. [ cita requerida ]
- Las estrellas cercanas, como la estrella de Barnard , se están moviendo hacia nosotros, lo que produce un desplazamiento al azul muy pequeño.
- El corrimiento al azul Doppler de objetos distantes con un z alto se puede restar del corrimiento al rojo cosmológico mucho mayor para determinar el movimiento relativo en el universo en expansión . [92]
Desplazamiento gravitacional hacia el azul

A diferencia del corrimiento al azul Doppler relativo , causado por el movimiento de una fuente hacia el observador y, por lo tanto, dependiente del ángulo recibido del fotón, el corrimiento al azul gravitacional es absoluto y no depende del ángulo recibido del fotón:
Los fotones que salen de un objeto gravitatorio pierden energía. Esta pérdida de energía se conoce como "desplazamiento al rojo", ya que los fotones en el espectro visible se verían más rojos. De manera similar, los fotones que caen en un campo gravitatorio se vuelven más energéticos y presentan un desplazamiento al azul. ... Nótese que la magnitud del efecto de desplazamiento al rojo (desplazamiento al azul) no es una función del ángulo emitido o del ángulo recibido del fotón, sino que depende únicamente de la distancia radial que el fotón tuvo que escalar para salir (caer) del pozo de potencial. [93] [94]
Es una consecuencia natural de la conservación de la energía y la equivalencia masa-energía , y se confirmó experimentalmente en 1959 con el experimento de Pound-Rebka . El corrimiento al azul gravitacional contribuye a la anisotropía del fondo cósmico de microondas (CMB) a través del efecto Sachs-Wolfe : cuando un pozo gravitacional evoluciona mientras un fotón está pasando, la cantidad de corrimiento al azul al acercarse diferirá de la cantidad de corrimiento al rojo gravitacional cuando abandona la región. [95]
Valores atípicos azules
Existen galaxias activas lejanas que muestran un corrimiento al azul en sus líneas de emisión [O III] . Uno de los corrimientos al azul más grandes se encuentra en el cuásar de línea estrecha , PG 1543+489 , que tiene una velocidad relativa de -1150 km/s. [92] Este tipo de galaxias se denominan "valores atípicos azules". [92]
Desplazamiento cosmológico al azul
En un universo hipotético que estuviera atravesando una contracción descontrolada por Big Crunch , se observaría un corrimiento cosmológico al azul, con galaxias más lejanas cada vez más desplazadas hacia el azul, exactamente lo opuesto del corrimiento al rojo cosmológico realmente observado en el universo en expansión actual . [ cita requerida ]
Véase también
Referencias
- ^ Ding, Qianhang (agosto de 2021). "Detectabilidad de sistemas binarios de agujeros negros primordiales a alto corrimiento al rojo". Physical Review D . 104 (4). id. 043527. arXiv : 2011.13643 . Código Bibliográfico :2021PhRvD.104d3527D. doi :10.1103/PhysRevD.104.043527.
- ^ Doppler, cristiano (1846). Beiträge zur fixsternenkunde . vol. 69. Praga: G. Haase Söhne. Código bibliográfico : 1846befi.book.....D.
- ^ Maulik, Dev (2005). "Ecografía Doppler: una breve historia". En Maulik, Dev; Zalud, Ivica (eds.). Ultrasonografía Doppler en obstetricia y ginecología. Springer. ISBN 978-3-540-23088-5.
- ^ O'Connor, John J.; Robertson, Edmund F. (1998). "Christian Andreas Doppler". Archivo de Historia de las Matemáticas de MacTutor . Universidad de St Andrews .
- ^ ab Huggins, William (1868). "Observaciones adicionales sobre los espectros de algunas estrellas y nebulosas, con un intento de determinar a partir de ellas si estos cuerpos se mueven hacia o desde la Tierra, también observaciones sobre los espectros del Sol y del cometa II". Philosophical Transactions of the Royal Society of London . 158 : 529–564. Bibcode :1868RSPT..158..529H. doi :10.1098/rstl.1868.0022.
- ^ Reber, G. (1995). "Plasma intergaláctico". Astrofísica y ciencia espacial . 227 (1–2): 93–96. Código Bibliográfico :1995Ap&SS.227...93R. doi :10.1007/BF00678069. S2CID 30000639.
- ^ Pannekoek, A. (1961). Una historia de la astronomía . Dover. pág. 451. ISBN 978-0-486-65994-7.
- ^ Bélopolsky, A. (1901). "Sobre un aparato para la demostración en laboratorio del principio Doppler-Fizeau". Astrophysical Journal . 13 : 15. Bibcode :1901ApJ....13...15B. doi : 10.1086/140786 .
- ^ Eddington, Arthur Stanley (1923). La teoría matemática de la relatividad. The University Press. pág. 164.
- ^ "corrimiento al rojo" . Oxford English Dictionary (edición en línea). Oxford University Press . Consultado el 17 de marzo de 2023 . (Se requiere suscripción o membresía a una institución participante).
- ^ de Sitter, W. (1934). "Sobre la distancia, la magnitud y las cantidades relacionadas en un universo en expansión". Boletín de los Institutos Astronómicos de los Países Bajos . 7 : 205. Bibcode :1934BAN.....7..205D.
Por lo tanto, se hace urgente investigar el efecto del corrimiento al rojo y de la métrica del universo sobre la magnitud aparente y el número observado de nebulosas de magnitud dada.
- ^ Slipher, Vesto (1912). "La velocidad radial de la nebulosa de Andrómeda". Boletín del Observatorio Lowell . 1 (8): 2.56–2.57. Bibcode :1913LowOB...2...56S.
La magnitud de esta velocidad, que es la mayor observada hasta ahora, plantea la cuestión de si el desplazamiento similar a la velocidad no podría deberse a alguna otra causa, pero creo que en la actualidad no tenemos otra interpretación para ello.
- ^ Slipher, Vesto (1915). "Observaciones espectrográficas de nebulosas". Astronomía popular . 23 : 21–24. Código Bibliográfico :1915PA.....23...21S.
- ^ Slipher, Vesto (1915). "Observaciones espectrográficas de nebulosas". Astronomía popular . 23 : 22. Bibcode :1915PA.....23...21S.
- ^ Hubble, Edwin (1929). "Una relación entre la distancia y la velocidad radial entre nebulosas extragalácticas". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 15 (3): 168–173. Bibcode :1929PNAS...15..168H. doi : 10.1073/pnas.15.3.168 . PMC 522427 . PMID 16577160.
- ^ "El universo se está expandiendo". 2017-12-08 . Consultado el 2023-09-06 .
- ^ Friedman, AA (1922). "Über die Krümmung des Raumes". Zeitschrift für Physik . 10 (1): 377–386. Código bibliográfico : 1922ZPhy...10..377F. doi :10.1007/BF01332580. S2CID 125190902.Traducción al inglés en Friedman, A. (1999). "Sobre la curvatura del espacio". Relatividad general y gravitación . 31 (12): 1991–2000. Bibcode :1999GReGr..31.1991F. doi :10.1023/A:1026751225741. S2CID 122950995.)
- ^ ab Los físicos y astrónomos que trabajaban en cosmología en la década de 1930 reconocieron esto desde el principio. La primera publicación para legos que describe los detalles de esta correspondencia es Eddington, Arthur (1933). The Expanding Universe: Astronomy's 'Great Debate', 1900–1931. Cambridge University Press .(Reimpresión: ISBN 978-0-521-34976-5 )
- ^ "El censo del Hubble descubre galaxias con corrimientos al rojo de entre 9 y 12". Nota de prensa de la ESA/Hubble . Consultado el 13 de diciembre de 2012 .
- ^ Véase, por ejemplo, este comunicado de prensa del 25 de mayo de 2004 del telescopio espacial Swift de la NASA , que investiga los estallidos de rayos gamma : "Las mediciones de los espectros de rayos gamma obtenidas durante el estallido principal del GRB han demostrado ser de poco valor como indicadores de corrimiento al rojo, debido a la falta de características bien definidas. Sin embargo, las observaciones ópticas de los resplandores del GRB han producido espectros con líneas identificables, lo que ha permitido realizar mediciones precisas del corrimiento al rojo".
- ^ Para un tutorial sobre cómo definir e interpretar mediciones de grandes corrimientos al rojo, consulte: Huchra, John. "Extragalactic Redshifts". Base de datos extragaláctica de la NASA/IPAC . Centro de Astrofísica Harvard-Smithsonian. Archivado desde el original el 22 de diciembre de 2013. Consultado el 16 de marzo de 2023 .
- ^ abcdefghi Véase Binney y Merrifeld (1998), Carroll y Ostlie (1996), Kutner (2003) para aplicaciones en astronomía.
- ^ Donde z = corrimiento al rojo; v || = velocidad paralela a la línea de visión (positiva si se aleja del receptor); c = velocidad de la luz ; γ = factor de Lorentz ; a = factor de escala ; G = constante gravitacional ; M = masa del objeto ; r = coordenada radial de Schwarzschild , g tt = componente t,t del tensor métrico
- ^ Ives, H.; Stilwell, G. (1938). "Un estudio experimental de la velocidad de un reloj atómico en movimiento". Revista de la Sociedad Óptica de América . 28 (7): 215–226. Bibcode :1938JOSA...28..215I. doi :10.1364/josa.28.000215.
- ^ Freund, Jurgen (2008). Relatividad especial para principiantes . World Scientific. pág. 120. ISBN 978-981-277-160-5.
- ^ Ditchburn, R. (1961). Luz . Dover. pág. 329. ISBN. 978-0-12-218101-6.
- ^ Véase "Fotones, relatividad, desplazamiento Doppler Archivado el 27 de agosto de 2006 en Wayback Machine " en la Universidad de Queensland
- ^ Bunn, EF; Hogg, DW (2009). "El origen cinemático del corrimiento al rojo cosmológico". American Journal of Physics . 77 (8): 688–694. arXiv : 0808.1081 . Código Bibliográfico :2009AmJPh..77..688B. doi :10.1119/1.3129103. S2CID 1365918.
- ^ Weinberg, Steven (1993). Los tres primeros minutos: una visión moderna del origen del universo (2.ª ed.). Basic Books. pág. 34. ISBN 9780-465-02437-7.
- ^ Bergström, Lars ; Goobar, Ariel (2006). Cosmología y astrofísica de partículas (2.ª ed.). Springer. pág. 77, Eq.4.79. ISBN 978-3-540-32924-4.
- ^ Longair, MS (1998). Formación de galaxias. Springer. pág. 161. ISBN 978-3-540-63785-1.
- ^ ab Staff (2015). «Calculadora cosmológica de la UCLA». UCLA . Consultado el 6 de agosto de 2022 .La distancia recorrida por la luz se calculó a partir del valor del corrimiento al rojo utilizando la calculadora cosmológica de la UCLA, con valores de parámetros a partir de 2015: H 0 = 67,74 y Omega M = 0,3089 (consulte la Tabla/Planck2015 en " Modelo Lambda-CDM#Parámetros ").
- ^ ab Staff (2018). «Calculadora cosmológica de la UCLA». UCLA . Consultado el 6 de agosto de 2022 .La distancia recorrida por la luz se calculó a partir del valor del corrimiento al rojo utilizando la Calculadora Cosmológica de la UCLA, con valores de parámetros a partir de 2018: H 0 = 67,4 y Omega M = 0,315 (consulte la Tabla/Planck2018 en " Modelo Lambda-CDM#Parámetros ")
- ^ ab Staff (2022). «Calculadora de cosmología ICRAR». Centro Internacional de Investigación en Radioastronomía . Consultado el 6 de agosto de 2022 .Calculadora de cosmología ICRAR: establezca H 0 = 67,4 y Omega M = 0,315 (consulte la Tabla/Planck2018 en " Modelo Lambda-CDM#Parámetros ")
- ^ ab Kempner, Joshua (2022). "Calculadora de cosmología KEMPNER". Kempner.net . Consultado el 6 de agosto de 2022 .Calculadora de cosmología KEMP: establezca H 0 = 67,4, Omega M = 0,315 y Omega Λ = 0,6847 (consulte la Tabla/Planck2018 en " Modelo Lambda-CDM#Parámetros ")
- ^ En 2003 , Karachentsev, ID; et al. (2003) informaron sobre mediciones de velocidades peculiares de hasta 5 Mpc utilizando el telescopio espacial Hubble . "Flujos locales de galaxias dentro de 5 Mpc". Astronomía y astrofísica . 398 (2): 479–491. arXiv : astro-ph/0211011 . Bibcode :2003A&A...398..479K. doi :10.1051/0004-6361:20021566. S2CID 26822121.
- ^ Koupelis, Theo; Kuhn, Karl F. (2007). En busca del universo (5.ª ed.). Jones & Bartlett Publishers. pág. 557. ISBN 978-0-7637-4387-1.
- ^ Lewis, Geraint F.; Francis, Matthew J.; Barnes, Luke A.; Kwan, Juliana; et al. (2008). "Cosmological Radar Ranging in an Expanding Universe" (Radar de medición cosmológica en un universo en expansión). Monthly Notices of the Royal Astronomical Society (Avisos mensuales de la Royal Astronomical Society ). 388 (3): 960–964. arXiv : 0805.2197 . Bibcode :2008MNRAS.388..960L. doi : 10.1111/j.1365-2966.2008.13477.x . S2CID 15147382.
Es perfectamente válido interpretar las ecuaciones de la relatividad en términos de un espacio en expansión. El error es llevar las analogías demasiado lejos e imbuir al espacio de propiedades físicas que no son consistentes con las ecuaciones de la relatividad.
- ^ Chodorowski, Michal (2007). "¿Realmente se está expandiendo el espacio? Un contraejemplo". Concepts Phys . 4 (1): 17–34. arXiv : astro-ph/0601171 . Bibcode :2007ONCP....4...15C. doi :10.2478/v10005-007-0002-2. S2CID 15931627.
- ^ Bedran, ML (2002). "Una comparación entre los corrimientos al rojo Doppler y cosmológico" (PDF) . American Journal of Physics . 70 (4): 406–408. Bibcode :2002AmJPh..70..406B. doi :10.1119/1.1446856 . Consultado el 16 de marzo de 2023 .
- ^ Harrison, Edward (1992). "Las leyes de desplazamiento al rojo-distancia y velocidad-distancia". Astrophysical Journal, Parte 1. 403 : 28–31. Bibcode :1993ApJ...403...28H. doi : 10.1086/172179 .. Un archivo pdf se puede encontrar aquí [1].
- ^ Harrison 2000, pág. 302.
- ^ Weinberg, Steven (2008). Cosmología. Oxford University Press. pág. 11. ISBN 978-0-19-852682-7.
- ^ Esto sólo es cierto en un universo donde no hay velocidades peculiares . De lo contrario, los desplazamientos al rojo se combinan como
- ^ Chant, CA (1930). "Notas y consultas (telescopios y equipos de observación: el desplazamiento de Einstein de las líneas solares)". Revista de la Real Sociedad Astronómica de Canadá . 24 : 390. Código Bibliográfico :1930JRASC..24..390C.
- ^ Einstein, A. (1907). "Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen". Jahrbuch der Radioaktivität und Elektronik . 4 : 411–462. Código bibliográfico : 1908JRE......4..411E.Véase la página 458 La influencia de un campo gravitacional en los relojes
- ^ Pound, R.; Rebka, G. (1960). "Peso aparente de los fotones". Physical Review Letters . 4 (7): 337–341. Código Bibliográfico :1960PhRvL...4..337P. doi : 10.1103/PhysRevLett.4.337 .Este documento fue la primera medición.
- ^ Sachs, RK ; Wolfe, AM (1967). "Perturbaciones de un modelo cosmológico y variaciones angulares del fondo cósmico de microondas". Astrophysical Journal . 147 (73): 73. Bibcode :1967ApJ...147...73S. doi :10.1086/148982.
- ^ desde SV Pilipenko (2013-2021) "Calculadora cosmológica de papel y lápiz" arxiv:1303.5961, incluido el código Fortran-90 en el que se basan los gráficos y fórmulas de citas.
- ^ Cuando se descubrieron por primera vez los corrimientos al rojo cosmológicos, Fritz Zwicky propuso un efecto conocido como luz cansada. Aunque normalmente se tiene en cuenta por intereses históricos, a veces, junto con sugerencias de corrimientos al rojo intrínsecos , se utiliza en cosmologías no estándar . En 1981, H. J. Reboul resumió muchos mecanismos alternativos de corrimiento al rojo que se habían discutido en la literatura desde la década de 1930. En 2001, Geoffrey Burbidge señaló en una revisión que la comunidad astronómica en general ha marginado tales discusiones desde la década de 1960. Burbidge y Halton Arp , mientras investigaban el misterio de la naturaleza de los cuásares , intentaron desarrollar mecanismos alternativos de corrimiento al rojo, y muy pocos de sus colegas científicos reconocieron y mucho menos aceptaron su trabajo. Además, Goldhaber, G.; et al. (2001). "Timescale Stretch Parameterization of Type Ia Supernova B-Band Lightcurves". Astrophysical Journal . 558 (1): 359–386. arXiv : astro-ph/0104382 . Código Bibliográfico :2001ApJ...558..359G. doi : 10.1086/322460 . S2CID 17237531.Señaló que las teorías alternativas no pueden explicar el estiramiento de la escala temporal observado en las supernovas de tipo Ia.
- ^ Para una revisión del tema de la fotometría, consulte: Budding, E. (24 de septiembre de 1993). Introducción a la fotometría astronómica . Cambridge University Press. ISBN 0-521-41867-4.
- ^ La técnica fue descrita por primera vez por: Baum, WA (1962). McVittie, GC (ed.). Problemas de la investigación extragaláctica . Simposio IAU No. 15. p. 390.
- ^ Bolzonella, M.; Miralles, J.-M.; Pelló, R. (2000). "Desplazamientos al rojo fotométricos basados en procedimientos de ajuste SED estándar". Astronomía y Astrofísica . 363 : 476–492. arXiv : astro-ph/0003380 . Código Bibliográfico :2000A&A...363..476B.
- ^ Se puede encontrar una descripción pedagógica de la corrección K por David Hogg y otros miembros de la colaboración SDSS en: Hogg, David W.; et al. (octubre de 2002). "La corrección K". arXiv : astro-ph/0210394 .
- ^ El Exoplanet Tracker es el proyecto de observación más reciente que utiliza esta técnica, capaz de rastrear las variaciones del corrimiento al rojo en múltiples objetos a la vez, como se informó en Ge, Jian; Van Eyken, Julian; Mahadevan, Suvrath ; Dewitt, Curtis; et al. (2006). "El primer planeta extrasolar descubierto con un instrumento Doppler de alto rendimiento de nueva generación". The Astrophysical Journal . 648 (1): 683–695. arXiv : astro-ph/0605247 . Bibcode :2006ApJ...648..683G. doi :10.1086/505699. S2CID 13879217.
- ^ Libbrecht, Keng (1988). "Sismología solar y estelar" (PDF) . Space Science Reviews . 47 (3–4): 275–301. Bibcode :1988SSRv...47..275L. doi :10.1007/BF00243557. S2CID 120897051.
- ^ En 1871, Hermann Carl Vogel midió la velocidad de rotación de Venus . Vesto Slipher estaba trabajando en tales mediciones cuando dirigió su atención a las nebulosas espirales.
- ^ Una revisión temprana de Oort, JH sobre el tema: Oort, JH (1970). "La formación de galaxias y el origen del hidrógeno de alta velocidad". Astronomía y Astrofísica . 7 : 381. Bibcode :1970A&A.....7..381O.
- ^ Asaoka, Ikuko (1989). "Espectros de rayos X en el infinito desde un disco de acreción relativista alrededor de un agujero negro de Kerr". Publicaciones de la Sociedad Astronómica de Japón . 41 (4): 763–778. Código Bibliográfico :1989PASJ...41..763A.
- ^ Rybicki, GB; Lightman, AR (1979). Procesos radiativos en astrofísica . John Wiley & Sons. pág. 288. ISBN 0-471-82759-2.
- ^ "Detectives cósmicos". Agencia Espacial Europea (ESA). 2 de abril de 2013. Consultado el 25 de abril de 2013 .
- ^ Se logró una medición precisa del fondo cósmico de microondas mediante el experimento COBE . La temperatura final publicada de 2,73 K se informó en este artículo: Fixsen, DJ; Cheng, ES; Cottingham, DA; Eplee, RE Jr.; Isaacman, RB; Mather, JC; Meyer, SS; Noerdlinger, PD; Shafer, RA; Weiss, R.; Wright, EL; Bennett, CL; Boggess, NW ; Kelsall, T.; Moseley, SH; Silverberg, RF; Smoot, GF; Wilkinson, DT (enero de 1994). "Espectro dipolar del fondo cósmico de microondas medido por el instrumento COBE FIRAS". Astrophysical Journal . 420 : 445. Bibcode :1994ApJ...420..445F. doi :10.1086/173575.La medición más precisa hasta 2006 se logró mediante el experimento WMAP .
- ^ abc Peebles (1993).
- ^ Binney, James; Treimane, Scott (1994). Dinámica galáctica . Princeton University Press. ISBN 978-0-691-08445-9.
- ^ "El Premio Nobel de Física 2011: Información para el público" (PDF) . nobelprize.org . Consultado el 13 de junio de 2023 .
- ^ Carniani, Stefano; Hainline, Kevin; D'Eugenio, Francesco; Eisenstein, Daniel J.; Jakobsen, Peter; Witstok, Joris; Johnson, Benjamin D.; Chevallard, Jacopo; Maiolino, Roberto; Helton, Jakob M.; Willott, Chris; Robertson, Brant; Alberts, Stacey; Arribas, Santiago; Baker, William M. (29 de julio de 2024). "Confirmación espectroscópica de dos galaxias luminosas con un corrimiento al rojo de 14". Nature . 633 (8029): 318–322. doi : 10.1038/s41586-024-07860-9 . ISSN 1476-4687. PMC 11390484 . PMID 39074505.
- ^ Oesch, PA; et al. (1 de marzo de 2016). "Una galaxia notablemente luminosa en z = 11,1 medida con la espectroscopia Grism del telescopio espacial Hubble". The Astrophysical Journal . 819 (2): 129. arXiv : 1603.00461 . Bibcode :2016ApJ...819..129O. doi : 10.3847/0004-637X/819/2/129 . S2CID 119262750.
- ^ Lehnert, MD; Nesvadba, NP; Cuby, JG; Swinbank, AM; et al. (2010). "Confirmación espectroscópica de una galaxia con un corrimiento al rojo z = 8,6". Nature . 467 (7318): 940–942. arXiv : 1010.4312 . Bibcode :2010Natur.467..940L. doi :10.1038/nature09462. PMID 20962840. S2CID 4414781.
- ^ Watson, Darach; Christensen, Lisa; Knudsen, Kirsten Kraiberg; Ricardo, Johan; Gallazzi, Anna; Michałowski, Michał Jerzy (2015). "Una galaxia normal y polvorienta en la época de la reionización". Naturaleza . 519 (7543): 327–330. arXiv : 1503.00002 . Código Bib :2015Natur.519..327W. doi : 10.1038/naturaleza14164. PMID 25731171. S2CID 2514879.
- ^ Bradley, LD; et al. (2008). "Descubrimiento de un candidato a galaxia muy brillante con efecto lente en z ~ 7,6". The Astrophysical Journal . 678 (2): 647–654. arXiv : 0802.2506 . Código Bibliográfico :2008ApJ...678..647B. doi :10.1086/533519. S2CID 15574239.
- ^ Egami, E.; et al. (2005). "Restricciones del telescopio espacial Spitzer y Hubble sobre las propiedades físicas de la galaxia z~7 fuertemente afectada por A2218". The Astrophysical Journal . 618 (1): L5–L8. arXiv : astro-ph/0411117 . Código Bibliográfico :2005ApJ...618L...5E. doi :10.1086/427550. S2CID 15920310.
- ^ Salvaterra, R.; Valle, M. Della; Campana, S.; Chincarini, G.; et al. (2009). "GRB 090423 revela una estrella en explosión en la época de la reionización". Nature . 461 (7268): 1258–60. arXiv : 0906.1578 . Bibcode :2009Natur.461.1258S. doi :10.1038/nature08445. PMID 19865166. S2CID 205218263.
- ^ Chu, Jennifer (6 de diciembre de 2017). "Los científicos observan un agujero negro supermasivo en el universo infantil". MIT News . Instituto Tecnológico de Massachusetts.
- ^ Bañados, Eduardo; Venemans, Bram P.; Mazzucchelli, Chiara; Farina, Emanuele P.; Walter, Fabian; Wang, Feige; Decarli, Roberto; Stern, Daniel; Fan, Xiaohui; Davies, Frederick B.; Hennawi, Joseph F.; Simcoe, Robert A.; Turner, Monica L.; Rix, Hans-Walter; Yang, Jinyi; Kelson, Daniel D.; Rudie, Gwen C.; Winters, Jan Martin (enero de 2018). "Un agujero negro de 800 millones de masas solares en un universo significativamente neutral con un corrimiento al rojo de 7,5". Nature . 553 (7689): 473–476. arXiv : 1712.01860 . Código Bibliográfico :2018Natur.553..473B. : Nature25180. PMID 29211709. S2CID 205263326.
- ^ Saxena, A. (2018). «Descubrimiento de una radiogalaxia en z = 5,72». Monthly Notices of the Royal Astronomical Society . 480 (2): 2733–2742. arXiv : 1806.01191 . Código Bibliográfico :2018MNRAS.480.2733S. doi : 10.1093/mnras/sty1996 . S2CID 118830412.
- ^ Walter, Fabian; Bertoldi, Frank; Carilli, Chris; Cox, Pierre; et al. (2003). "Gas molecular en la galaxia anfitriona de un cuásar con un corrimiento al rojo z = 6,42". Nature . 424 (6947): 406–8. arXiv : astro-ph/0307410 . Bibcode :2003Natur.424..406W. doi :10.1038/nature01821. PMID 12879063. S2CID 4419009.
- ^ Smail, Ian; Owen, FN; Morrison, GE; Keel, WC; et al. (2002). "La diversidad de objetos extremadamente rojos". The Astrophysical Journal . 581 (2): 844–864. arXiv : astro-ph/0208434 . Bibcode :2002ApJ...581..844S. doi :10.1086/344440. S2CID 51737034.
- ^ Totani, Tomonori; Yoshii, Yuzuru; Iwamuro, Fumihide; Maihara, Toshinori; et al. (2001). "Objetos hiperextremadamente rojos en el campo profundo de Subaru: evidencia de galaxias elípticas primordiales en la fase Dusty Starburst". La revista astrofísica . 558 (2): L87-L91. arXiv : astro-ph/0108145 . Código Bib : 2001ApJ...558L..87T. doi :10.1086/323619. S2CID 119511017.
- ^ Lineweaver, Charles; Davis, Tamara M. (2005). "Ideas erróneas sobre el Big Bang". Scientific American . 292 (3): 36–45. Bibcode :2005SciAm.292c..36L. doi :10.1038/scientificamerican0305-36.
- ^ Naoz, S.; Noter, S.; Barkana, R. (2006). "Las primeras estrellas en el Universo". Monthly Notices of the Royal Astronomical Society: Letters . 373 (1): L98–L102. arXiv : astro-ph/0604050 . Código Bibliográfico :2006MNRAS.373L..98N. doi : 10.1111/j.1745-3933.2006.00251.x . S2CID 14454275.
- ^ Lesgourgues, J; Pastor, S (2006). "Neutrinos masivos y cosmología". Physics Reports . 429 (6): 307–379. arXiv : astro-ph/0603494 . Código Bibliográfico :2006PhR...429..307L. doi :10.1016/j.physrep.2006.04.001. S2CID 5955312.
- ^ Grishchuk, Leonid P (2005). "Ondas gravitacionales reliquia y cosmología". Physics-Uspekhi . 48 (12): 1235–1247. arXiv : gr-qc/0504018 . Código Bibliográfico :2005PhyU...48.1235G. doi :10.1070/PU2005v048n12ABEH005795. S2CID 11957123.
- ^ Sobral, David; Matthee, Jorryt; Darvish, Behnam; Schärer, Daniel; Mobasher, Bahram; Röttgering, Huub JA; Santos, Sergio; Hemmati, Shoubaneh (4 de junio de 2015). "Evidencia de poblaciones estelares similares a POPIII en los emisores LYMAN-α más luminosos en la época de la reionización: confirmación espectroscópica". La revista astrofísica . 808 (2): 139. arXiv : 1504.01734 . Código Bib : 2015ApJ...808..139S. doi :10.1088/0004-637x/808/2/139. S2CID 18471887.
- ^ Overbye, Dennis (17 de junio de 2015). "Los astrónomos informan que encontraron las primeras estrellas que enriquecieron el cosmos". The New York Times . Consultado el 17 de junio de 2015 .
- ^ Geller, MJ; Huchra, JP (1989). "Mapping the Universe" (Mapeando el universo). Science . 246 (4932): 897–903. Bibcode :1989Sci...246..897G. doi :10.1126/science.246.4932.897. PMID 17812575. S2CID 31328798.
- ^ Consulte el sitio web del CfA para obtener más detalles: Huchra, John P. "The CfA Redshift Survey". Centro de Astrofísica Harvard & Smithsonian . Consultado el 20 de marzo de 2023 .
- ^ Cole, Shaun ; Percival, Will J.; Peacock, John A.; Norberg, Peder; et al. (2005). "El estudio del corrimiento al rojo de galaxias 2dF: análisis del espectro de potencia del conjunto de datos final e implicaciones cosmológicas". Monthly Notices of the Royal Astronomical Society . 362 (2): 505–34. arXiv : astro-ph/0501174 . Código Bibliográfico :2005MNRAS.362..505C. doi : 10.1111/j.1365-2966.2005.09318.x . S2CID 6906627.Página de inicio de la encuesta sobre el corrimiento al rojo de la galaxia 2dF Archivado el 5 de febrero de 2007 en Wayback Machine
- ^ "SDSS-III". www.sdss3.org . Consultado el 20 de marzo de 2023 .
- ^ Davis, Marc; Colaboración DEEP2 (2002). Objetivos científicos y primeros resultados del sondeo de corrimiento al rojo DEEP2 . Conferencia sobre telescopios astronómicos e instrumentación, Waikoloa, Hawai, 22-28 de agosto de 2002. arXiv : astro-ph/0209419 . Código Bibliográfico :2003SPIE.4834..161D. doi :10.1117/12.457897.
{{cite conference}}: CS1 maint: numeric names: authors list (link) - ^ Kuhn, Karl F.; Koupelis, Theo (2004). En busca del universo . Jones & Bartlett Publishers . págs. 122-3. ISBN 978-0-7637-0810-8.
- ^ Woodhouse, Chris (4 de diciembre de 2017). "M31 (galaxia de Andrómeda)". Manual de astrofotografía (2.ª ed.). Routledge. págs. 308-313. doi :10.4324/9781315159225-42. ISBN . 978-1-315-15922-5.
- ^ abc Aoki, Kentaro; Kawaguchi, Toshihiro; Ohta, Kouji (enero de 2005). "Los mayores desplazamientos al azul de la línea de emisión [O III] en dos cuásares de línea estrecha". Astrophysical Journal . 618 (2): 601–608. arXiv : astro-ph/0409546 . Código Bibliográfico :2005ApJ...618..601A. doi :10.1086/426075. S2CID 17680991.
- ^ Nemiroff, RJ (1993). "Principios gravitacionales y matemáticas". NASA .
- ^ Nemiroff, RJ (1993). "Distorsiones visuales cerca de una estrella de neutrones y un agujero negro". American Journal of Physics . 61 (7): 619–632. arXiv : astro-ph/9312003v1 . Código Bibliográfico :1993AmJPh..61..619N. doi :10.1119/1.17224. S2CID 16640860.
- ^ Bonometto, Silvio; Gorini, Vittorio; Moschella, Ugo (2002). Cosmología moderna . Prensa CRC . ISBN 978-0-7503-0810-6.
Fuentes
Artículos
- Odenwald, S. y Fienberg, RT. 1993; "Galaxy Redshifts Reconsidered" en Sky & Telescope, febrero de 2003; págs. 31-35 (este artículo es una lectura adicional útil para distinguir entre los tres tipos de corrimiento al rojo y sus causas).
- Lineweaver, Charles H. y Tamara M. Davis, "Misconceptions about the Big Bang", Scientific American , marzo de 2005. (Este artículo es útil para explicar el mecanismo del corrimiento al rojo cosmológico, así como para aclarar conceptos erróneos sobre la física de la expansión del espacio.)
Libros
- Nussbaumer, Harry; Lidia Bieri (2009). Descubriendo el Universo en Expansión . Prensa de la Universidad de Cambridge. ISBN 978-0-521-51484-2.
- Binney, James; Michael Merrifeld (1998). Astronomía galáctica . Princeton University Press. ISBN 978-0-691-02565-0.
- Carroll, Bradley W. y Dale A. Ostlie (1996). Introducción a la astrofísica moderna . Addison-Wesley Publishing Company, Inc. ISBN 978-0-201-54730-6.
- Feynman, Richard; Leighton, Robert; Sands, Matthew (1989). Feynman Lectures on Physics. Vol. 1. Addison-Wesley. ISBN. 978-0-201-51003-4.
- Grøn, Øyvind ; Hervik, Sigbjørn (2007). Teoría General de la Relatividad de Einstein . Nueva York: Springer. ISBN 978-0-387-69199-2.
- Harrison, Edward (2000). Cosmología: la ciencia del universo (2.ª ed.). Cambridge University Press. ISBN 978-0-521-66148-5.
- Kutner, Marc (2003). Astronomía: una perspectiva física . Cambridge University Press. ISBN 978-0-521-52927-3.
- Misner, Charles; Thorne, Kip S.; Wheeler, John Archibald (1973). Gravitación . San Francisco: WH Freeman. ISBN 978-0-7167-0344-0.
- Peebles, PJE (1993). Principios de cosmología física. Princeton University Press. ISBN 978-0-691-01933-8.
- Taylor, Edwin F.; Wheeler, John Archibald (1992). Física del espacio-tiempo: Introducción a la relatividad especial (2.ª ed.). WH Freeman. ISBN 978-0-7167-2327-1.
- Weinberg, Steven (1971). Gravitación y cosmología. John Wiley. ISBN 978-0-471-92567-5.
- Consulte también los libros de texto de cosmología física para obtener aplicaciones de los desplazamientos al rojo cosmológicos y gravitacionales.
Enlaces externos
- Tutorial de cosmología de Ned Wright
- Entrada de la guía de referencia cósmica sobre el corrimiento al rojo
- Tutorial de Mike Luciuk sobre el corrimiento al rojo astronómico
- GIF animado del corrimiento al rojo cosmológico de Wayne Hu
- Merrifield, Michael; Hill, Richard (2009). "Z Redshift". SIXTψ SYMBΦLS . Brady Haran para la Universidad de Nottingham .







































