Punto de fuga

Un punto de fuga es un punto en el plano de la imagen de una representación en perspectiva donde las proyecciones en perspectiva bidimensionales de líneas paralelas entre sí en el espacio tridimensional parecen converger. Cuando el conjunto de líneas paralelas es perpendicular a un plano de la imagen , la construcción se conoce como perspectiva de un punto, y su punto de fuga corresponde al óculo , o "punto del ojo", desde el que se debe ver la imagen para obtener una geometría de perspectiva correcta. ^[1] Los dibujos lineales tradicionales utilizan objetos con uno a tres conjuntos de paralelos, que definen uno a tres puntos de fuga.

Parte de una serie sobre
Proyección gráfica
Planar Proyección paralela Proyección ortográfica Proyección isométrica Proyección oblicua Proyección en perspectiva Perspectiva curvilínea Perspectiva inversa
Vistas Vista de pájaro Sección transversal Dibujo en corte Dibujo de vista en despiece Lente ojo de pez Vistas múltiples Panorama Vista desde el punto de vista del gusano Objetivo zoom
Temas Proyección 3D Anamorfosis Axonometría Gráficos de computadora Diseño asistido por ordenador Geometría descriptiva Dibujo de ingeniería Proyección de mapas Plano de imagen Planos (dibujos) Proyección (álgebra lineal) Plano de proyección Geometría proyectiva Estereoscopia Dibujo técnico Longitud real Punto de fuga Gráficos de videojuegos Visualización del tronco truncado
en a mi

El erudito humanista y arquitecto italiano Leon Battista Alberti introdujo por primera vez el concepto en su tratado sobre la perspectiva en el arte, De pictura , escrito en 1435. ^[2] Las vías de tren rectas son un ejemplo moderno conocido. ^[3]

El punto de fuga también puede denominarse "punto de dirección", ya que las líneas que tienen el mismo vector direccional, digamos D , tendrán el mismo punto de fuga. Matemáticamente, sea q ≡ ( x , y , f ) un punto que se encuentra en el plano de la imagen, donde f es la distancia focal (de la cámara asociada con la imagen), y sea v _q ≡ ( ⁠incógnita/yo⁠ , ⁠y/yo⁠ , ⁠F/yo⁠ ) ​​sea el vector unitario asociado a q , donde h = √ x ² + y ² + f ² . Si consideramos una línea recta en el espacio S con el vector unitario n _s ≡ ( n _x , n _y , n _z ) y su punto de fuga v _s , el vector unitario asociado a v _s es igual a n _s , asumiendo que ambos apuntan hacia el plano imagen. ^[4]

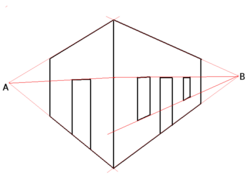
Cuando el plano de la imagen es paralelo a dos ejes de coordenadas del mundo, las líneas paralelas al eje que corta este plano de la imagen tendrán imágenes que se encuentran en un único punto de fuga. Las líneas paralelas a los otros dos ejes no formarán puntos de fuga, ya que son paralelas al plano de la imagen. Esta es la perspectiva de un punto. De manera similar, cuando el plano de la imagen interseca dos ejes de coordenadas del mundo, las líneas paralelas a esos planos se encontrarán y formarán dos puntos de fuga en el plano de la imagen. Esto se llama perspectiva de dos puntos. En la perspectiva de tres puntos, el plano de la imagen interseca los ejes x , y y z y, por lo tanto, las líneas paralelas a estos ejes se intersecan, lo que da como resultado tres puntos de fuga diferentes.

El teorema del punto de fuga es el teorema principal en la ciencia de la perspectiva. Dice que la imagen en un plano de imagen π de una línea L en el espacio, no paralela a la imagen, está determinada por su intersección con π y su punto de fuga. Algunos autores han usado la frase, "la imagen de una línea incluye su punto de fuga". Guidobaldo del Monte dio varias verificaciones, y Humphry Ditton llamó al resultado la "principal y Gran Proposición". ^[5] Brook Taylor escribió el primer libro en inglés sobre perspectiva en 1714, que introdujo el término "punto de fuga" y fue el primero en explicar completamente la geometría de la perspectiva multipunto, y la historiadora Kirsti Andersen recopiló estas observaciones. ^{[1] : 244–6} Ella señala, en términos de geometría proyectiva , que el punto de fuga es la imagen del punto en el infinito asociado con L , ya que la línea de visión desde O a través del punto de fuga es paralela a L .

Así como un punto de fuga se origina en una línea, una línea de fuga se origina en un plano α que no es paralelo a la imagen π . Dado el punto del ojo O , y β el plano paralelo a α y que se encuentra sobre O , entonces la línea de fuga de α es β ∩ π . Por ejemplo, cuando α es el plano del suelo y β es el plano del horizonte, entonces la línea de fuga de α es la línea del horizonte β ∩ π .

En términos simples, la línea de fuga de un plano, digamos α , se obtiene por la intersección del plano de la imagen con otro plano, digamos β , paralelo al plano de interés ( α ), que pasa por el centro de la cámara. Para diferentes conjuntos de líneas paralelas a este plano α , sus respectivos puntos de fuga estarán en esta línea de fuga. La línea del horizonte es una línea teórica que representa el nivel de los ojos del observador. Si el objeto está debajo de la línea del horizonte, sus líneas forman un ángulo hacia arriba con respecto a la línea del horizonte. Si el objeto está arriba, se inclinan hacia abajo.

1. Las proyecciones de dos conjuntos de líneas paralelas que se encuentran en algún plano π _A parecen converger, es decir, el punto de fuga asociado con ese par, en una línea de horizonte, o línea de fuga H formada por la intersección del plano de la imagen con el plano paralelo a π _A y que pasa a través del orificio. Demostración: considere el plano de tierra π , como y = c que es, por el bien de la simplicidad, ortogonal al plano de la imagen. Además, considere una línea L que se encuentra en el plano π , que se define por la ecuación ax + bz = d . Usando proyecciones en perspectiva de orificios, un punto en L proyectado en el plano de la imagen tendrá coordenadas definidas como,

x′ = f · ⁠incógnita/el⁠ = f · ⁠d - bz/Arizona⁠

y′ = f · ⁠y/el⁠ = f · ⁠do/el⁠

Esta es la representación paramétrica de la imagen L′ de la recta L con z como parámetro. Cuando z → −∞ se detiene en el punto ( x′ , y′ ) = (− ⁠pensión completa/a⁠ ,0) en el eje x′ del plano de la imagen. Este es el punto de fuga correspondiente a todas las líneas paralelas con pendiente − ⁠b/a⁠ en el plano π . Todos los puntos de fuga asociados a diferentes líneas con diferentes pendientes pertenecientes al plano π estarán en el eje x′ , que en este caso es la línea del horizonte.

2. Sean A , B y C tres rectas mutuamente ortogonales en el espacio y v _A ≡ ( x _A , y _A , f ) , v _B ≡ ( x _B , y _B , f ) , v _C ≡ ( x _C , y _C , f ) los tres puntos de fuga correspondientes respectivamente. Si conocemos las coordenadas de uno de estos puntos, digamos v _A , y la dirección de una recta en el plano de la imagen, que pasa por un segundo punto, digamos v _B , podemos calcular las coordenadas tanto de v _B como de v _C ^[4]

3. Sean A , B y C tres rectas mutuamente ortogonales en el espacio y v _A ≡ ( x _A , y _A , f ) , v _B ≡ ( x _B , y _B , f ) , v _C ≡ ( x _C , y _C , f ) los tres puntos de fuga correspondientes respectivamente. El ortocentro del triángulo con vértices en los tres puntos de fuga es la intersección del eje óptico y el plano de la imagen. ^[4]

Una perspectiva curvilínea es un dibujo con 4 o 5 puntos de fuga. En la perspectiva de 5 puntos, los puntos de fuga se trazan en un círculo con 4 puntos de fuga en los puntos cardinales N, W, S, E y uno en el origen del círculo.

Una perspectiva inversa es un dibujo con puntos de fuga que se colocan fuera del cuadro con la ilusión de que están "delante" del cuadro.

• 
  Proyección en perspectiva de un solo punto.
• 
  Perspectiva de un solo punto en fotografía
• 
  Proyección en perspectiva de doble punto.
• 
  El uso de la perspectiva que hizo Pietro Perugino en el fresco de la Entrega de las llaves en la Capilla Sixtina (1481-1482) contribuyó a llevar el Renacimiento a Roma.

Varios métodos para la detección de puntos de fuga utilizan los segmentos de línea detectados en las imágenes. Otras técnicas implican considerar directamente los gradientes de intensidad de los píxeles de la imagen.

En una imagen hay una cantidad significativamente grande de puntos de fuga. Por lo tanto, el objetivo es detectar los puntos de fuga que corresponden a las direcciones principales de una escena. Esto generalmente se logra en dos pasos. El primer paso, llamado paso de acumulación, como sugiere el nombre, agrupa los segmentos de línea con la suposición de que un grupo tendrá un punto de fuga común. El siguiente paso encuentra los grupos principales presentes en la escena y, por lo tanto, se llama paso de búsqueda.

En el paso de acumulación , la imagen se mapea en un espacio acotado llamado espacio acumulador. El espacio acumulador se divide en unidades llamadas celdas. Barnard ^[6] asumió que este espacio era una esfera gaussiana centrada en el centro óptico de la cámara como un espacio acumulador. Un segmento de línea en la imagen corresponde a un gran círculo en esta esfera, y el punto de fuga en la imagen se mapea a un punto. La esfera gaussiana tiene celdas acumuladoras que aumentan cuando un gran círculo pasa a través de ellas, es decir, en la imagen un segmento de línea interseca el punto de fuga. Se han realizado varias modificaciones desde entonces, pero una de las técnicas más eficientes fue usar la Transformada de Hough , mapeando los parámetros del segmento de línea al espacio acotado. Las Transformadas de Hough en cascada se han aplicado para múltiples puntos de fuga.

El proceso de mapeo de la imagen a los espacios delimitados provoca la pérdida de las distancias reales entre los segmentos de línea y los puntos.

En el paso de búsqueda , se encuentra la celda del acumulador con el número máximo de segmentos de línea que pasan por ella. A continuación, se eliminan esos segmentos de línea y se repite el paso de búsqueda hasta que este recuento desciende por debajo de un cierto umbral. Como ahora hay más potencia de cálculo disponible, se pueden encontrar puntos correspondientes a dos o tres direcciones mutuamente ortogonales.

1. Calibración de la cámara: los puntos de fuga de una imagen contienen información importante para la calibración de la cámara. Se han introducido varias técnicas de calibración que utilizan las propiedades de los puntos de fuga para encontrar parámetros de calibración intrínsecos y extrínsecos. ^[7]
2. Reconstrucción 3D : Un entorno creado por el hombre tiene dos características principales: varias líneas en la escena son paralelas y una serie de bordes presentes son ortogonales. Los puntos de fuga ayudan a comprender el entorno. Usando conjuntos de líneas paralelas en el plano, la orientación del plano se puede calcular usando puntos de fuga. Torre ^[8] y Coelho ^[9] realizaron una investigación exhaustiva en el uso de puntos de fuga para implementar un sistema completo. Con la suposición de que el entorno consiste en objetos con solo lados paralelos o perpendiculares, también llamado Lego-land, usando puntos de fuga construidos en una sola imagen de la escena, recuperaron la geometría 3D de la escena. También se utilizan ideas similares en el campo de la robótica, principalmente en navegación y vehículos autónomos, y en áreas relacionadas con la detección de objetos .

• Proyección gráfica

• Detección del punto de fuga mediante tres algoritmos diferentes propuestos
• Detección de puntos de fuga para imágenes y vídeos mediante Open CV
• Un tutorial que cubre muchos ejemplos de perspectiva lineal.
• Cálculo trigonométrico de puntos de fuga Breve explicación del fundamento con un ejemplo sencillo