Oscilador armónico

Parte de una serie sobre
Mecánica clásica
${\displaystyle {\textbf {F}}={\frac {d\mathbf {p} }{dt}}}$ Second law of motion
History Timeline Textbooks
Branches Applied Celestial Continuum Dynamics Kinematics Kinetics Statics Statistical mechanics
Fundamentals Acceleration Angular momentum Couple D'Alembert's principle Energy kinetic potential Force Frame of reference Inertial frame of reference Impulse Inertia / Moment of inertia Mass Mechanical power Mechanical work Moment Momentum Space Speed Time Torque Velocity Virtual work
Formulations Newton's laws of motion Analytical mechanics Lagrangian mechanics Hamiltonian mechanics Routhian mechanics Hamilton–Jacobi equation Appell's equation of motion Koopman–von Neumann mechanics
Core topics Damping Displacement Equations of motion Euler's laws of motion Fictitious force Friction Harmonic oscillator Inertial / Non-inertial reference frame Mechanics of planar particle motion Motion (linear) Newton's law of universal gravitation Newton's laws of motion Relative velocity Rigid body dynamics Euler's equations Simple harmonic motion Vibration
Rotation Circular motion Rotating reference frame Centripetal force Centrifugal force reactive Coriolis force Pendulum Tangential speed Rotational frequency Angular acceleration / displacement / frequency / velocity
Scientists Kepler Galileo Huygens Newton Horrocks Halley Maupertuis Daniel Bernoulli Johann Bernoulli Euler d'Alembert Clairaut Lagrange Laplace Poisson Hamilton Jacobi Cauchy Routh Liouville Appell Gibbs Koopman von Neumann
Physics portal  Category
v t e

En mecánica clásica , un oscilador armónico es un sistema que, cuando se desplaza desde su posición de equilibrio , experimenta una fuerza restauradora F proporcional al desplazamiento x : F → = − k x → , {\displaystyle {\vec {F}}=-k{\vec {x}},} donde k es una constante positiva .

Si F es la única fuerza que actúa sobre el sistema, el sistema se denomina oscilador armónico simple y experimenta un movimiento armónico simple : oscilaciones sinusoidales alrededor del punto de equilibrio, con una amplitud constante y una frecuencia constante (que no depende de la amplitud).

Si además existe una fuerza de fricción ( amortiguación ) proporcional a la velocidad , el oscilador armónico se describe como oscilador amortiguado . Dependiendo del coeficiente de fricción, el sistema puede:

• Oscila con una frecuencia menor que en el caso no amortiguado y una amplitud que decrece con el tiempo ( oscilador subamortiguado ).
• Decaimiento hasta la posición de equilibrio, sin oscilaciones ( oscilador sobreamortiguado ).

La solución límite entre un oscilador subamortiguado y un oscilador sobreamortiguado ocurre en un valor particular del coeficiente de fricción y se denomina amortiguamiento crítico .

Si está presente una fuerza externa dependiente del tiempo, el oscilador armónico se describe como un oscilador impulsado .

Los ejemplos mecánicos incluyen péndulos (con pequeños ángulos de desplazamiento ), masas conectadas a resortes y sistemas acústicos . Otros sistemas análogos incluyen osciladores armónicos eléctricos como circuitos RLC . El modelo de oscilador armónico es muy importante en física, porque cualquier masa sujeta a una fuerza en equilibrio estable actúa como un oscilador armónico para pequeñas vibraciones. Los osciladores armónicos se encuentran ampliamente en la naturaleza y se explotan en muchos dispositivos fabricados por el hombre, como relojes y circuitos de radio. Son la fuente de prácticamente todas las vibraciones y ondas sinusoidales.

Un oscilador armónico simple es un oscilador que no está ni excitado ni amortiguado . Consiste en una masa m , que experimenta una única fuerza F , que tira de la masa en la dirección del punto x = 0 y depende únicamente de la posición x de la masa y de una constante k . El equilibrio de fuerzas ( segunda ley de Newton ) para el sistema es$${\displaystyle F=ma=m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=m{\ddot {x}}=-kx.}$$

Resolviendo esta ecuación diferencial , encontramos que el movimiento está descrito por la función x ( t ) = A sin ⁡ ( ω t + φ ) , {\displaystyle x(t)=A\sin(\omega t+\varphi ),} donde ω = k m . {\displaystyle \omega ={\sqrt {\frac {k}{m}}}.}

El movimiento es periódico y se repite de forma sinusoidal con una amplitud constante A. Además de su amplitud, el movimiento de un oscilador armónico simple se caracteriza por su período , el tiempo de una sola oscilación o su frecuencia , el número de ciclos por unidad de tiempo. La posición en un momento dado t también depende de la fase φ , que determina el punto de partida en la onda sinusoidal. El período y la frecuencia están determinados por el tamaño de la masa m y la constante de fuerza k , mientras que la amplitud y la fase están determinadas por la posición inicial y la velocidad .${\displaystyle T=2\pi /\omega }$${\displaystyle f=1/T}$

La velocidad y la aceleración de un oscilador armónico simple oscilan con la misma frecuencia que la posición, pero con fases desplazadas. La velocidad es máxima para un desplazamiento cero, mientras que la aceleración es en dirección opuesta al desplazamiento.

La energía potencial almacenada en un oscilador armónico simple en la posición x es U = 1 2 k x 2 . {\displaystyle U={\tfrac {1}{2}}kx^{2}.}

En los osciladores reales, la fricción, o amortiguación, ralentiza el movimiento del sistema. Debido a la fuerza de fricción, la velocidad disminuye en proporción a la fuerza de fricción que actúa. Mientras que en un oscilador armónico simple no accionado la única fuerza que actúa sobre la masa es la fuerza restauradora, en un oscilador armónico amortiguado hay además una fuerza de fricción que siempre está en una dirección que se opone al movimiento. En muchos sistemas vibratorios, la fuerza de fricción F _f se puede modelar como proporcional a la velocidad v del objeto: F _f = − cv , donde c se denomina coeficiente de amortiguamiento viscoso .

El equilibrio de fuerzas ( segunda ley de Newton ) para osciladores armónicos amortiguados es entonces ^{[1] [2] [3]} que puede reescribirse en la forma donde$${\displaystyle F=-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}}=m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}},}$$$${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x=0,}$$

• ${\textstyle \omega _{0}={\sqrt {\frac {k}{m}}}}$se llama " frecuencia angular no amortiguada del oscilador",
• ζ = c 2 m k {\textstyle \zeta ={\frac {c}{2{\sqrt {mk}}}}} se denomina "coeficiente de amortiguamiento".

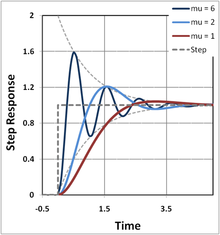
El valor del coeficiente de amortiguamiento ζ determina de forma crítica el comportamiento del sistema. Un oscilador armónico amortiguado puede ser:

• Sobreamortiguado ( ζ > 1): el sistema retorna ( decae exponencialmente ) al estado estacionario sin oscilar. Los valores mayores del coeficiente de amortiguamiento ζ retornarán al equilibrio más lentamente.
• Amortiguación crítica ( ζ = 1): el sistema vuelve al estado estable lo más rápido posible sin oscilar (aunque puede producirse un sobreimpulso si la velocidad inicial no es cero). Esto suele ser deseable para la amortiguación de sistemas como las puertas.
• Subamortiguado ( ζ < 1): el sistema oscila (con una frecuencia ligeramente diferente a la del caso no amortiguado) con una amplitud que disminuye gradualmente hasta cero. La frecuencia angular del oscilador armónico subamortiguado está dada por la desintegración exponencial del oscilador armónico subamortiguado está dada por${\textstyle \omega _{1}=\omega _{0}{\sqrt {1-\zeta ^{2}}},}$${\displaystyle \lambda =\omega _{0}\zeta .}$

El factor Q de un oscilador amortiguado se define como $${\displaystyle Q=2\pi \times {\frac {\text{energy stored}}{\text{energy lost per cycle}}}.}$$

Q está relacionada con la relación de amortiguamiento por${\textstyle Q={\frac {1}{2\zeta }}.}$

Los osciladores armónicos accionados son osciladores amortiguados que además se ven afectados por una fuerza aplicada externamente F ( t ).

La segunda ley de Newton toma la forma$${\displaystyle F(t)-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}}=m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}.}$$

Generalmente se reescribe en la forma$${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {F(t)}{m}}.}$$

Esta ecuación se puede resolver exactamente para cualquier fuerza impulsora, utilizando las soluciones z ( t ) que satisfacen la ecuación no forzada$${\displaystyle {\frac {\mathrm {d} ^{2}z}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} z}{\mathrm {d} t}}+\omega _{0}^{2}z=0,}$$

y que pueden expresarse como oscilaciones sinusoidales amortiguadas: en el caso en que ζ ≤ 1 . La amplitud A y la fase φ determinan el comportamiento necesario para adaptarse a las condiciones iniciales.$${\displaystyle z(t)=Ae^{-\zeta \omega _{0}t}\sin \left({\sqrt {1-\zeta ^{2}}}\omega _{0}t+\varphi \right),}$$

En el caso ζ < 1 y una entrada de paso unitario con  x (0) = 0 : la solución es$${\displaystyle {\frac {F(t)}{m}}={\begin{cases}\omega _{0}^{2}&t\geq 0\\0&t<0\end{cases}}}$$$${\displaystyle x(t)=1-e^{-\zeta \omega _{0}t}{\frac {\sin \left({\sqrt {1-\zeta ^{2}}}\omega _{0}t+\varphi \right)}{\sin(\varphi )}},}$$

con fase φ dada por

$${\displaystyle \cos \varphi =\zeta .}$$

El tiempo que necesita un oscilador para adaptarse a las condiciones externas modificadas es del orden de τ = 1/( ζω ₀ ) . En física, la adaptación se denomina relajación y τ se denomina tiempo de relajación.

En ingeniería eléctrica, un múltiplo de τ se denomina tiempo de establecimiento , es decir, el tiempo necesario para garantizar que la señal se encuentre dentro de una desviación fija del valor final, normalmente dentro del 10 %. El término sobreimpulso se refiere al grado en que el máximo de respuesta excede el valor final, y subimpulso se refiere al grado en que la respuesta cae por debajo del valor final para tiempos posteriores al máximo de respuesta.

En el caso de una fuerza impulsora sinusoidal: donde es la amplitud de impulso y es la frecuencia de impulso para un mecanismo impulsor sinusoidal. Este tipo de sistema aparece en circuitos RLC accionados por CA ( resistor – inductor – condensador ) y sistemas de resorte accionados que tienen resistencia mecánica interna o resistencia de aire externa .$${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {1}{m}}F_{0}\sin(\omega t),}$$${\displaystyle F_{0}}$${\displaystyle \omega }$

La solución general es una suma de una solución transitoria que depende de las condiciones iniciales y un estado estable que es independiente de las condiciones iniciales y depende solo de la amplitud de activación , la frecuencia de activación , la frecuencia angular no amortiguada y la relación de amortiguamiento .${\displaystyle F_{0}}$${\displaystyle \omega }$${\displaystyle \omega _{0}}$${\displaystyle \zeta }$

La solución de estado estable es proporcional a la fuerza impulsora con un cambio de fase inducido : donde Z m = ( 2 ω 0 ζ ) 2 + 1 ω 2 ( ω 0 2 − ω 2 ) 2 {\displaystyle Z_{m}={\sqrt {\left(2\omega _{0}\zeta \right)^{2}+{\frac {1}{\omega ^{2}}}(\omega _{0}^{2}-\omega ^{2})^{2}}}} es el valor absoluto de la impedancia o función de respuesta lineal , y${\displaystyle \varphi }$$${\displaystyle x(t)={\frac {F_{0}}{mZ_{m}\omega }}\sin(\omega t+\varphi ),}$$$${\displaystyle \varphi =\arctan \left({\frac {2\omega \omega _{0}\zeta }{\omega ^{2}-\omega _{0}^{2}}}\right)+n\pi }$$

es la fase de la oscilación con respecto a la fuerza impulsora. El valor de la fase se considera generalmente entre −180° y 0 (es decir, representa un desfase, tanto para los valores positivos como negativos del argumento arctan).

Para una frecuencia de excitación particular llamada resonancia o frecuencia resonante , la amplitud (para una determinada ) es máxima. Este efecto de resonancia solo se produce cuando , es decir, para sistemas significativamente subamortiguados. Para sistemas fuertemente subamortiguados, el valor de la amplitud puede llegar a ser bastante grande cerca de la frecuencia resonante.${\textstyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}}$${\displaystyle F_{0}}$${\displaystyle \zeta <1/{\sqrt {2}}}$

Las soluciones transitorias son las mismas que las del oscilador armónico amortiguado no forzado ( ) y representan la respuesta del sistema a otros eventos que ocurrieron anteriormente. Las soluciones transitorias suelen desaparecer con la suficiente rapidez como para que se las pueda ignorar.${\displaystyle F_{0}=0}$

Un oscilador paramétrico es un oscilador armónico accionado en el que la energía de accionamiento se proporciona variando los parámetros del oscilador, como la fuerza de amortiguación o restauración. Un ejemplo conocido de oscilación paramétrica es el "bombeo" en un columpio de patio de recreo . ^{[4] [5] [6]} Una persona en un columpio en movimiento puede aumentar la amplitud de las oscilaciones del columpio sin que se aplique ninguna fuerza de accionamiento externa (empujones), cambiando el momento de inercia del columpio balanceándose hacia adelante y hacia atrás ("bombeo") o alternativamente de pie y en cuclillas, al ritmo de las oscilaciones del columpio. La variación de los parámetros impulsa el sistema. Ejemplos de parámetros que pueden variarse son su frecuencia de resonancia y amortiguación .${\displaystyle \omega }$${\displaystyle \beta }$

Los osciladores paramétricos se utilizan en muchas aplicaciones. El oscilador paramétrico varactor clásico oscila cuando la capacitancia del diodo varía periódicamente. El circuito que varía la capacitancia del diodo se denomina "bomba" o "controlador". En la electrónica de microondas, los osciladores paramétricos basados ​​en guías de ondas / YAG funcionan de la misma manera. El diseñador varía un parámetro periódicamente para inducir oscilaciones.

Los osciladores paramétricos se han desarrollado como amplificadores de bajo ruido, especialmente en el rango de frecuencias de radio y microondas. El ruido térmico es mínimo, ya que se varía una reactancia (no una resistencia). Otro uso común es la conversión de frecuencia, por ejemplo, la conversión de frecuencias de audio a frecuencias de radio. Por ejemplo, el oscilador paramétrico óptico convierte una onda láser de entrada en dos ondas de salida de menor frecuencia ( ).${\displaystyle \omega _{s},\omega _{i}}$

La resonancia paramétrica se produce en un sistema mecánico cuando un sistema se excita paramétricamente y oscila en una de sus frecuencias de resonancia. La excitación paramétrica se diferencia de la excitación forzada, ya que la acción aparece como una modificación que varía con el tiempo en un parámetro del sistema. Este efecto es diferente de la resonancia regular porque presenta el fenómeno de inestabilidad .

La ecuación se conoce como ecuación del oscilador universal , ya que todos los sistemas oscilatorios lineales de segundo orden pueden reducirse a esta forma. ^{[ cita requerida ]} Esto se hace mediante la adimensionalización .$${\displaystyle {\frac {\mathrm {d} ^{2}q}{\mathrm {d} \tau ^{2}}}+2\zeta {\frac {\mathrm {d} q}{\mathrm {d} \tau }}+q=0}$$

Si la función de forzamiento es f ( t ) = cos( ωt ) = cos( ωt _c τ ) = cos( ωτ ) , donde ω = ωt _c , la ecuación se convierte en$${\displaystyle {\frac {\mathrm {d} ^{2}q}{\mathrm {d} \tau ^{2}}}+2\zeta {\frac {\mathrm {d} q}{\mathrm {d} \tau }}+q=\cos(\omega \tau ).}$$

La solución de esta ecuación diferencial contiene dos partes: la "transitoria" y la "estacionaria".

La solución basada en resolver la ecuación diferencial ordinaria es para constantes arbitrarias c ₁ y c ₂

$${\displaystyle q_{t}(\tau )={\begin{cases}e^{-\zeta \tau }\left(c_{1}e^{\tau {\sqrt {\zeta ^{2}-1}}}+c_{2}e^{-\tau {\sqrt {\zeta ^{2}-1}}}\right)&\zeta >1{\text{ (overdamping)}}\\e^{-\zeta \tau }(c_{1}+c_{2}\tau )=e^{-\tau }(c_{1}+c_{2}\tau )&\zeta =1{\text{ (critical damping)}}\\e^{-\zeta \tau }\left[c_{1}\cos \left({\sqrt {1-\zeta ^{2}}}\tau \right)+c_{2}\sin \left({\sqrt {1-\zeta ^{2}}}\tau \right)\right]&\zeta <1{\text{ (underdamping)}}\end{cases}}}$$

La solución transitoria es independiente de la función de forzamiento.

Aplique el " método de variables complejas " resolviendo la ecuación auxiliar a continuación y luego encontrando la parte real de su solución:$${\displaystyle {\frac {\mathrm {d} ^{2}q}{\mathrm {d} \tau ^{2}}}+2\zeta {\frac {\mathrm {d} q}{\mathrm {d} \tau }}+q=\cos(\omega \tau )+i\sin(\omega \tau )=e^{i\omega \tau }.}$$

Suponiendo que la solución es de la forma$${\displaystyle q_{s}(\tau )=Ae^{i(\omega \tau +\varphi )}.}$$

Sus derivadas de orden cero a segundo son$${\displaystyle q_{s}=Ae^{i(\omega \tau +\varphi )},\quad {\frac {\mathrm {d} q_{s}}{\mathrm {d} \tau }}=i\omega Ae^{i(\omega \tau +\varphi )},\quad {\frac {\mathrm {d} ^{2}q_{s}}{\mathrm {d} \tau ^{2}}}=-\omega ^{2}Ae^{i(\omega \tau +\varphi )}.}$$

Sustituyendo estas cantidades en la ecuación diferencial se obtiene$${\displaystyle -\omega ^{2}Ae^{i(\omega \tau +\varphi )}+2\zeta i\omega Ae^{i(\omega \tau +\varphi )}+Ae^{i(\omega \tau +\varphi )}=(-\omega ^{2}A+2\zeta i\omega A+A)e^{i(\omega \tau +\varphi )}=e^{i\omega \tau }.}$$

Dividir por el término exponencial de la izquierda da como resultado$${\displaystyle -\omega ^{2}A+2\zeta i\omega A+A=e^{-i\varphi }=\cos \varphi -i\sin \varphi .}$$

Igualar las partes reales e imaginarias da como resultado dos ecuaciones independientes$${\displaystyle A(1-\omega ^{2})=\cos \varphi ,\quad 2\zeta \omega A=-\sin \varphi .}$$

Elevando al cuadrado ambas ecuaciones y sumándolas obtenemos$${\displaystyle \left.{\begin{aligned}A^{2}(1-\omega ^{2})^{2}&=\cos ^{2}\varphi \\(2\zeta \omega A)^{2}&=\sin ^{2}\varphi \end{aligned}}\right\}\Rightarrow A^{2}[(1-\omega ^{2})^{2}+(2\zeta \omega )^{2}]=1.}$$

Por lo tanto,$${\displaystyle A=A(\zeta ,\omega )=\operatorname {sgn} \left({\frac {-\sin \varphi }{2\zeta \omega }}\right){\frac {1}{\sqrt {(1-\omega ^{2})^{2}+(2\zeta \omega )^{2}}}}.}$$

Compare este resultado con la sección de teoría sobre resonancia , así como con la "parte de magnitud" del circuito RLC . Esta función de amplitud es particularmente importante en el análisis y la comprensión de la respuesta de frecuencia de los sistemas de segundo orden.

Para resolver φ , divide ambas ecuaciones para obtener$${\displaystyle \tan \varphi =-{\frac {2\zeta \omega }{1-\omega ^{2}}}={\frac {2\zeta \omega }{\omega ^{2}-1}}~~\implies ~~\varphi \equiv \varphi (\zeta ,\omega )=\arctan \left({\frac {2\zeta \omega }{\omega ^{2}-1}}\right)+n\pi .}$$

Esta función de fase es particularmente importante en el análisis y la comprensión de la respuesta de frecuencia de sistemas de segundo orden.

La combinación de las porciones de amplitud y fase da como resultado la solución de estado estable.$${\displaystyle q_{s}(\tau )=A(\zeta ,\omega )\cos(\omega \tau +\varphi (\zeta ,\omega ))=A\cos(\omega \tau +\varphi ).}$$

La solución de la ecuación del oscilador universal original es una superposición (suma) de las soluciones transitoria y de estado estable:$${\displaystyle q(\tau )=q_{t}(\tau )+q_{s}(\tau ).}$$

Los osciladores armónicos que se producen en diversas áreas de la ingeniería son equivalentes en el sentido de que sus modelos matemáticos son idénticos (véase la ecuación del oscilador universal más arriba). A continuación se muestra una tabla que muestra cantidades análogas en cuatro sistemas de osciladores armónicos en mecánica y electrónica. Si a parámetros análogos en la misma línea de la tabla se les asignan valores numéricamente iguales, el comportamiento de los osciladores (su forma de onda de salida, frecuencia de resonancia, factor de amortiguamiento, etc.) es el mismo.

Mecánica traslacional	Mecánica rotacional	Circuito RLC en serie	Circuito RLC paralelo
Posición${\displaystyle x}$	Ángulo${\displaystyle \theta }$	Cargar ${\displaystyle q}$	Enlace de flujo ${\displaystyle \varphi }$
Velocidad ${\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} t}}}$	Velocidad angular ${\displaystyle {\frac {\mathrm {d} \theta }{\mathrm {d} t}}}$	Actual ${\displaystyle {\frac {\mathrm {d} q}{\mathrm {d} t}}}$	Voltaje ${\displaystyle {\frac {\mathrm {d} \varphi }{\mathrm {d} t}}}$
Masa ${\displaystyle m}$	Momento de inercia ${\displaystyle I}$	Inductancia ${\displaystyle L}$	Capacidad ${\displaystyle C}$
Impulso ${\displaystyle p}$	Momento angular ${\displaystyle L}$	Enlace de flujo ${\displaystyle \varphi }$	Cargar ${\displaystyle q}$
Constante de resorte ${\displaystyle k}$	Constante de torsión ${\displaystyle \mu }$	Elastancia ${\displaystyle 1/C}$	Reluctancia magnética ${\displaystyle 1/L}$
Mojadura ${\displaystyle c}$	Fricción rotacional ${\displaystyle \Gamma }$	Resistencia ${\displaystyle R}$	Conductancia ${\displaystyle G=1/R}$
Fuerza motriz ${\displaystyle F(t)}$	Par motor ${\displaystyle \tau (t)}$	Voltaje ${\displaystyle v}$	Actual ${\displaystyle i}$
Frecuencia de resonancia no amortiguada :${\displaystyle f_{n}}$
${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {k}{m}}}}$	${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {\mu }{I}}}}$	${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {1}{LC}}}}$	${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {1}{LC}}}}$
Relación de amortiguamiento :${\displaystyle \zeta }$
${\displaystyle {\frac {c}{2}}{\sqrt {\frac {1}{km}}}}$	${\displaystyle {\frac {\Gamma }{2}}{\sqrt {\frac {1}{I\mu }}}}$	${\displaystyle {\frac {R}{2}}{\sqrt {\frac {C}{L}}}}$	${\displaystyle {\frac {G}{2}}{\sqrt {\frac {L}{C}}}}$
Ecuación diferencial:
${\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=F}$	${\displaystyle I{\ddot {\theta }}+\Gamma {\dot {\theta }}+\mu \theta =\tau }$	${\displaystyle L{\ddot {q}}+R{\dot {q}}+q/C=v}$	${\displaystyle C{\ddot {\varphi }}+G{\dot {\varphi }}+\varphi /L=i}$

El problema del oscilador armónico simple ocurre con frecuencia en física, porque una masa en equilibrio bajo la influencia de cualquier fuerza conservativa , en el límite de pequeños movimientos, se comporta como un oscilador armónico simple.

Una fuerza conservativa es aquella que está asociada a una energía potencial . La función de energía potencial de un oscilador armónico es$${\displaystyle V(x)={\tfrac {1}{2}}kx^{2}.}$$

Dada una función de energía potencial arbitraria , se puede hacer una expansión de Taylor en términos de alrededor de un mínimo de energía ( ) para modelar el comportamiento de pequeñas perturbaciones del equilibrio.${\displaystyle V(x)}$${\displaystyle x}$${\displaystyle x=x_{0}}$

$${\displaystyle V(x)=V(x_{0})+V'(x_{0})\cdot (x-x_{0})+{\tfrac {1}{2}}V''(x_{0})\cdot (x-x_{0})^{2}+O(x-x_{0})^{3}.}$$

Como es un mínimo, la primera derivada evaluada en debe ser cero, por lo que el término lineal se elimina:${\displaystyle V(x_{0})}$${\displaystyle x_{0}}$$${\displaystyle V(x)=V(x_{0})+{\tfrac {1}{2}}V''(x_{0})\cdot (x-x_{0})^{2}+O(x-x_{0})^{3}.}$$

El término constante V ( x ₀ ) es arbitrario y, por lo tanto, puede eliminarse, y una transformación de coordenadas permite recuperar la forma del oscilador armónico simple:$${\displaystyle V(x)\approx {\tfrac {1}{2}}V''(0)\cdot x^{2}={\tfrac {1}{2}}kx^{2}.}$$

Así, dada una función de energía potencial arbitraria con una segunda derivada que no se desvanece, se puede utilizar la solución del oscilador armónico simple para proporcionar una solución aproximada para pequeñas perturbaciones alrededor del punto de equilibrio.${\displaystyle V(x)}$

Suponiendo que no hay amortiguamiento, la ecuación diferencial que gobierna un péndulo simple de longitud , donde es la aceleración local de la gravedad , es d 2 θ d t 2 + g l sin ⁡ θ = 0. {\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{l}}\sin \theta =0.} ${\displaystyle l}$${\displaystyle g}$

Si el desplazamiento máximo del péndulo es pequeño, podemos utilizar la aproximación y en su lugar considerar la ecuación${\displaystyle \sin \theta \approx \theta }$$${\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{l}}\theta =0.}$$

La solución general de esta ecuación diferencial es donde y son constantes que dependen de las condiciones iniciales. Usando como condiciones iniciales y , la solución viene dada por donde es el ángulo más grande alcanzado por el péndulo (es decir, es la amplitud del péndulo). El período , el tiempo para una oscilación completa, viene dado por la expresión τ = 2 π l g = 2 π ω , {\displaystyle \tau =2\pi {\sqrt {\frac {l}{g}}}={\frac {2\pi }{\omega }},} que es una buena aproximación del período real cuando es pequeño. Nótese que en esta aproximación el período es independiente de la amplitud . En la ecuación anterior, representa la frecuencia angular.$${\displaystyle \theta (t)=A\cos \left({\sqrt {\frac {g}{l}}}t+\varphi \right),}$$${\displaystyle A}$${\displaystyle \varphi }$${\displaystyle \theta (0)=\theta _{0}}$${\displaystyle {\dot {\theta }}(0)=0}$$${\displaystyle \theta (t)=\theta _{0}\cos \left({\sqrt {\frac {g}{l}}}t\right),}$$${\displaystyle \theta _{0}}$${\displaystyle \theta _{0}}$${\displaystyle \theta _{0}}$${\displaystyle \tau }$${\displaystyle \theta _{0}}$${\displaystyle \omega }$

Cuando una masa estira o comprime un resorte, éste desarrolla una fuerza restauradora. La ley de Hooke proporciona la relación de la fuerza ejercida por el resorte cuando se comprime o estira una cierta longitud: donde F es la fuerza, k es la constante del resorte y x es el desplazamiento de la masa con respecto a la posición de equilibrio. El signo menos en la ecuación indica que la fuerza ejercida por el resorte siempre actúa en una dirección opuesta al desplazamiento (es decir, la fuerza siempre actúa hacia la posición cero), y así evita que la masa salga volando hacia el infinito.$${\displaystyle F(t)=-kx(t),}$$

Utilizando un método de equilibrio de fuerzas o de energía, se puede demostrar fácilmente que el movimiento de este sistema está dado por la siguiente ecuación diferencial: siendo esta última la segunda ley del movimiento de Newton .$${\displaystyle F(t)=-kx(t)=m{\frac {\mathrm {d} ^{2}}{\mathrm {d} t^{2}}}x(t)=ma,}$$

Si el desplazamiento inicial es A y no hay velocidad inicial, la solución de esta ecuación viene dada por$${\displaystyle x(t)=A\cos \left({\sqrt {\frac {k}{m}}}t\right).}$$

Dado un resorte ideal sin masa, es la masa en el extremo del resorte. Si el resorte en sí tiene masa, su masa efectiva debe incluirse en .${\displaystyle m}$${\displaystyle m}$

En términos de energía, todos los sistemas tienen dos tipos de energía: energía potencial y energía cinética . Cuando un resorte se estira o se comprime, almacena energía potencial elástica, que luego se transfiere a energía cinética. La energía potencial dentro de un resorte está determinada por la ecuación${\textstyle U={\frac {1}{2}}kx^{2}.}$

Cuando el resorte se estira o se comprime, la energía cinética de la masa se convierte en energía potencial del resorte. Por conservación de la energía, suponiendo que el punto de referencia está definido en la posición de equilibrio, cuando el resorte alcanza su energía potencial máxima, la energía cinética de la masa es cero. Cuando se suelta el resorte, intenta volver al equilibrio y toda su energía potencial se convierte en energía cinética de la masa.

Símbolo	Definición	Dimensiones	Unidades del SI
${\displaystyle a}$	Aceleración de la masa	${\displaystyle {\mathsf {LT^{-2}}}}$	m/ s2
${\displaystyle A}$	Amplitud máxima de oscilación	${\displaystyle {\mathsf {L}}}$	metro
${\displaystyle c}$	Coeficiente de amortiguamiento viscoso	${\displaystyle {\mathsf {MT^{-1}}}}$	N·s/m
${\displaystyle f}$	Frecuencia	${\displaystyle {\mathsf {T^{-1}}}}$	Hz
${\displaystyle F}$	Fuerza motriz	${\displaystyle {\mathsf {MLT^{-2}}}}$	norte
${\displaystyle g}$	Aceleración de la gravedad en la superficie de la Tierra.	${\displaystyle {\mathsf {LT^{-2}}}}$	m/ s2
${\displaystyle i}$	Unidad imaginaria,${\displaystyle i^{2}=-1}$	—	—
${\displaystyle k}$	Constante de resorte	${\displaystyle {\mathsf {MT^{-2}}}}$	Nuevo Méjico
${\displaystyle \mu }$	Constante del resorte de torsión	${\displaystyle {\mathsf {ML^{2}T^{-2}}}}$	Nm/rad
${\displaystyle m,M}$	Masa	${\displaystyle {\mathsf {M}}}$	kilogramo
${\displaystyle Q}$	Factor de calidad	—	—
${\displaystyle T}$	Periodo de oscilación	${\displaystyle {\mathsf {T}}}$	s
${\displaystyle t}$	Tiempo	${\displaystyle {\mathsf {T}}}$	s
${\displaystyle U}$	Energía potencial almacenada en el oscilador	${\displaystyle {\mathsf {ML^{2}T^{-2}}}}$	Yo
${\displaystyle x}$	Posición de la masa	${\displaystyle {\mathsf {L}}}$	metro
${\displaystyle \zeta }$	Relación de amortiguamiento	—	—
${\displaystyle \varphi }$	Cambio de fase	—	Radial
${\displaystyle \omega }$	Frecuencia angular	${\displaystyle {\mathsf {T^{-1}}}}$	radio/s
${\displaystyle \omega _{0}}$	Frecuencia angular resonante natural	${\displaystyle {\mathsf {T^{-1}}}}$	radio/s

• Fowles, Grant R.; Cassiday, George L. (1986), Mecánica analítica (5.ª ed.), Fort Worth: Saunders College Publishing , ISBN 0-03-089725-4, N.º de código de la LCCN  93085193
• Hayek, Sabih I. (15 de abril de 2003). "Vibración mecánica y amortiguamiento". Enciclopedia de física aplicada . WILEY-VCH Verlag GmbH & Co KGaA. doi :10.1002/3527600434.eap231. ISBN 9783527600434.
• Kreyszig, Erwin (1972), Matemáticas avanzadas de ingeniería (3.ª ed.), Nueva York: Wiley , ISBN 0-471-50728-8
• Serway, Raymond A.; Jewett, John W. (2003). Física para científicos e ingenieros. Brooks/Cole. ISBN 0-534-40842-7.
• Tipler, Paul (1998). Física para científicos e ingenieros: vol. 1 (4.ª ed.). WH Freeman. ISBN 1-57259-492-6.
• Wylie, CR (1975). Matemáticas avanzadas para ingeniería (4.ª ed.). McGraw-Hill. ISBN 0-07-072180-7.

Wikimedia Commons tiene medios relacionados con Osciladores armónicos .

Wikiquote tiene citas relacionadas con Oscilador armónico .

• El oscilador armónico de las Conferencias Feynman sobre física