Defecto cristalográfico

Un defecto cristalográfico es una interrupción de los patrones regulares de disposición de átomos o moléculas en sólidos cristalinos . Las posiciones y orientaciones de las partículas, que se repiten a distancias fijas determinadas por los parámetros de la celda unitaria en los cristales, exhiben una estructura cristalina periódica , pero esta suele ser imperfecta. ^{[2] [3] [4] [5]} A menudo se caracterizan varios tipos de defectos: defectos puntuales, defectos lineales, defectos planares, defectos en masa. La homotopía topológica establece un método matemático de caracterización.

Los defectos puntuales son defectos que ocurren solo en o alrededor de un único punto de la red. No se extienden en el espacio en ninguna dimensión. Por lo general, no se definen explícitamente límites estrictos sobre cuán pequeño es un defecto puntual. Sin embargo, estos defectos generalmente involucran como máximo unos pocos átomos adicionales o faltantes. Los defectos más grandes en una estructura ordenada generalmente se consideran bucles de dislocación . Por razones históricas, muchos defectos puntuales, especialmente en cristales iónicos, se denominan centros : por ejemplo, una vacante en muchos sólidos iónicos se denomina centro de luminiscencia, centro de color o centro F. Estas dislocaciones permiten el transporte iónico a través de cristales que conducen a reacciones electroquímicas. Con frecuencia se especifican utilizando la notación de Kröger-Vink .

• Los defectos de vacancia son sitios de la red que estarían ocupados en un cristal perfecto, pero que están vacantes. Si un átomo vecino se mueve para ocupar el sitio vacante, la vacancia se mueve en la dirección opuesta al sitio que solía estar ocupado por el átomo en movimiento. La estabilidad de la estructura cristalina circundante garantiza que los átomos vecinos no colapsen simplemente alrededor de la vacancia. En algunos materiales, los átomos vecinos en realidad se alejan de una vacancia, porque experimentan atracción de los átomos de los alrededores. Una vacancia (o un par de vacantes en un sólido iónico) a veces se denomina defecto de Schottky .
• Los defectos intersticiales son átomos que ocupan un sitio en la estructura cristalina en el que normalmente no hay un átomo . Por lo general, son configuraciones de alta energía. Los átomos pequeños (en su mayoría impurezas) en algunos cristales pueden ocupar intersticios sin alta energía, como el hidrógeno en el paladio .

• Un par cercano de una vacante y un intersticial se suele denominar defecto de Frenkel o par de Frenkel. Esto se produce cuando un ion se desplaza hacia un sitio intersticial y crea una vacante.

• Debido a las limitaciones fundamentales de los métodos de purificación de materiales, los materiales nunca son 100% puros, lo que por definición induce defectos en la estructura cristalina. En el caso de una impureza, el átomo a menudo se incorpora en un sitio atómico regular en la estructura cristalina. Este no es un sitio vacante ni el átomo está en un sitio intersticial y se llama defecto de sustitución . Se supone que el átomo no está en ninguna parte del cristal y, por lo tanto, es una impureza. En algunos casos donde el radio del átomo (ion) de sustitución es sustancialmente menor que el del átomo (ion) que está reemplazando, su posición de equilibrio puede desplazarse lejos del sitio reticular. Estos tipos de defectos de sustitución a menudo se denominan iones descentrados . Hay dos tipos diferentes de defectos de sustitución: sustitución isovalente y sustitución aliovalente. La sustitución isovalente es donde el ion que está sustituyendo al ion original tiene el mismo estado de oxidación que el ion que está reemplazando. La sustitución aliovalente es aquella en la que el ion que sustituye al ion original tiene un estado de oxidación diferente al del ion que reemplaza. Las sustituciones aliovalentes cambian la carga general dentro del compuesto iónico, pero el compuesto iónico debe ser neutro. Por lo tanto, se requiere un mecanismo de compensación de carga. Por lo tanto, uno de los metales se oxida o reduce parcial o totalmente, o se crean vacantes iónicas.
• Los defectos antisitio ^{[6] [7]} ocurren en una aleación o compuesto ordenado cuando átomos de diferentes tipos intercambian posiciones. Por ejemplo, algunas aleaciones tienen una estructura regular en la que cada átomo de por medio es de una especie diferente; a modo de ilustración, supongamos que los átomos de tipo A se ubican en las esquinas de una red cúbica y los átomos de tipo B se ubican en el centro de los cubos. Si un cubo tiene un átomo A en su centro, el átomo está en un sitio que normalmente está ocupado por un átomo B y, por lo tanto, es un defecto antisitio. Esto no es ni una vacante ni un intersticial ni una impureza.
• Los defectos topológicos son regiones de un cristal en las que el entorno de enlace químico normal es topológicamente diferente del entorno. Por ejemplo, en una lámina perfecta de grafito ( grafeno ), todos los átomos están en anillos que contienen seis átomos. Si la lámina contiene regiones en las que el número de átomos en un anillo es diferente de seis, mientras que el número total de átomos permanece igual, se ha formado un defecto topológico. Un ejemplo es el defecto de Stone Wales en los nanotubos, que consta de dos anillos de átomos adyacentes de 5 miembros y dos de 7 miembros.

• Los sólidos amorfos pueden contener defectos. Naturalmente, estos son algo difíciles de definir, pero a veces su naturaleza se puede entender con bastante facilidad. Por ejemplo, en sílice amorfa con enlaces ideales , todos los átomos de Si tienen 4 enlaces con átomos de O y todos los átomos de O tienen 2 enlaces con un átomo de Si. Por lo tanto, por ejemplo, un átomo de O con un solo enlace de Si (un enlace colgante ) puede considerarse un defecto en sílice. ^[8] Además, los defectos también se pueden definir en sólidos amorfos en función de vecindarios atómicos locales vacíos o densamente empaquetados, y se puede demostrar que las propiedades de dichos "defectos" son similares a las vacantes e intersticiales normales en los cristales. ^{[9] [10] [11]}
• Los complejos pueden formarse entre distintos tipos de defectos puntuales. Por ejemplo, si una vacante se encuentra con una impureza, ambas pueden unirse si la impureza es demasiado grande para la red. Los intersticiales pueden formar estructuras "intersticiales divididas" o "mancuernas" en las que dos átomos comparten efectivamente un sitio atómico, lo que hace que ninguno de los átomos ocupe realmente el sitio. ^{[12] [13]}

Los defectos de línea se pueden describir mediante teorías de calibre.

Las dislocaciones son defectos lineales alrededor de los cuales los átomos de la red cristalina están desalineados. ^[14] Existen dos tipos básicos de dislocaciones: la dislocación de borde y la dislocación helicoidal . También son comunes las dislocaciones "mixtas", que combinan aspectos de ambos tipos.

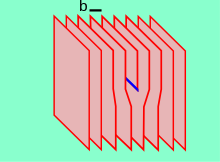
Las dislocaciones de borde se producen por la terminación de un plano de átomos en el medio de un cristal. En tal caso, los planos adyacentes no son rectos, sino que se curvan alrededor del borde del plano de terminación de modo que la estructura cristalina está perfectamente ordenada en ambos lados. La analogía con una pila de papel es apropiada: si se inserta media hoja de papel en una pila de papeles, el defecto en la pila solo se nota en el borde de la media hoja.

La dislocación helicoidal es más difícil de visualizar, pero básicamente comprende una estructura en la que se traza una trayectoria helicoidal alrededor del defecto lineal (línea de dislocación) por los planos atómicos de los átomos en la red cristalina.

La presencia de dislocaciones produce una deformación reticular (distorsión). La dirección y magnitud de dicha distorsión se expresa en términos de un vector de Burgers (b). Para un tipo de arista, b es perpendicular a la línea de dislocación, mientras que en los casos del tipo tornillo es paralela. En los materiales metálicos, b está alineada con direcciones cristalográficas compactas y su magnitud es equivalente a un espaciamiento interatómico.

Las dislocaciones pueden moverse si los átomos de uno de los planos circundantes rompen sus enlaces y se vuelven a unir con los átomos en el borde terminal.

Es la presencia de dislocaciones y su capacidad de moverse fácilmente (e interactuar) bajo la influencia de tensiones inducidas por cargas externas lo que conduce a la maleabilidad característica de los materiales metálicos.

Las dislocaciones se pueden observar mediante microscopía electrónica de transmisión , microscopía de iones de campo y técnicas de sonda atómica . La espectroscopia transitoria de nivel profundo se ha utilizado para estudiar la actividad eléctrica de las dislocaciones en semiconductores, principalmente silicio .

Las disclinaciones son defectos lineales que corresponden a la "adición" o "reducción" de un ángulo alrededor de una línea. Básicamente, esto significa que si se sigue la orientación del cristal alrededor del defecto lineal, se obtiene una rotación. Por lo general, se pensaba que desempeñaban un papel solo en los cristales líquidos, pero los desarrollos recientes sugieren que también podrían tener un papel en los materiales sólidos, por ejemplo, provocando la autocuración de las grietas . ^[15]

• Los límites de grano se producen cuando la dirección cristalográfica de la red cambia abruptamente. Esto suele ocurrir cuando dos cristales comienzan a crecer por separado y luego se encuentran.
• Los límites antifásicos se producen en aleaciones ordenadas: en este caso, la dirección cristalográfica sigue siendo la misma, pero cada lado del límite tiene una fase opuesta: por ejemplo, si el ordenamiento es habitualmente ABABABAB ( cristal hexagonal compacto ), un límite antifásico toma la forma de ABABBABA.
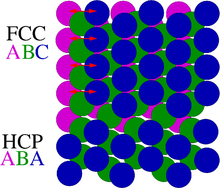
• Las fallas de apilamiento se producen en diversas estructuras cristalinas, pero el ejemplo más común es el de las estructuras compactas . Se forman por una desviación local de la secuencia de apilamiento de capas en un cristal. Un ejemplo sería la secuencia de apilamiento ABABCABAB.
• Un límite maclado es un defecto que introduce un plano de simetría especular en el ordenamiento de un cristal. Por ejemplo, en cristales cúbicos compactos , la secuencia de apilamiento de un límite maclado sería ABCABCBACBA.
• En los planos de monocristales , los escalones entre terrazas atómicamente planas también pueden considerarse defectos planos. Se ha demostrado que dichos defectos y su geometría tienen una influencia significativa en la adsorción de moléculas orgánicas ^[16]

• Defectos macroscópicos o volumétricos tridimensionales, como poros, grietas o inclusiones.
• Vacíos: pequeñas regiones donde no hay átomos y que pueden considerarse como grupos de vacantes.
• Las impurezas pueden agruparse para formar pequeñas regiones de una fase diferente. Estas suelen denominarse precipitados .

Un método de clasificación matemática exitoso para defectos físicos de red, que funciona no sólo con la teoría de dislocaciones y otros defectos en cristales sino también, por ejemplo, para disclinaciones en cristales líquidos y para excitaciones en 3He superfluido ^, es la teoría de homotopía topológica . ^[17]

La teoría funcional de la densidad , la dinámica molecular clásica y las simulaciones cinéticas de Monte Carlo ^[18] se utilizan ampliamente para estudiar las propiedades de los defectos en sólidos con simulaciones por computadora. ^{[9] [10] [11] [ 19] [20] [21] [22]} Simular el atasco de esferas duras de diferentes tamaños y/o en contenedores con tamaños no mensurables utilizando el algoritmo de Lubachevsky-Stillinger puede ser una técnica eficaz para demostrar algunos tipos de defectos cristalográficos. ^[23]

• Defecto de Bjerrum
• Defectos cristalográficos en el diamante
• Notación de Kröger-Vink
• F-centro

• Hagen Kleinert , Campos de calibración en materia condensada , vol. II, "Tensiones y defectos", págs. 743-1456, World Scientific (Singapur, 1989); ISBN de tapa blanda 9971-5-0210-0 
• Hermann Schmalzried : Reacciones de estado sólido . Verlag Chemie, Weinheim 1981, ISBN 3-527-25872-8 .