ISO 216
La introducción de este artículo puede ser demasiado breve para resumir adecuadamente los puntos clave . ( Junio de 2023 ) |


La norma ISO 216 es una norma internacional para tamaños de papel que se utiliza en todo el mundo, excepto en América del Norte y algunas partes de América Latina. La norma define las series de tamaños de papel " A ", " B " y " C ", que incluyen el tamaño de papel A4 , el más comúnmente disponible en todo el mundo. Dos normas complementarias, ISO 217 e ISO 269 , definen tamaños de papel relacionados; la serie " C " de ISO 269 se incluye comúnmente junto con los tamaños A y B.
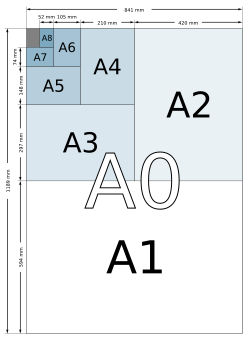
Todos los tamaños de papel ISO 216, ISO 217 e ISO 269 (excepto algunos sobres) tienen la misma relación de aspecto , √ 2 :1 , con un margen de redondeo de milímetros . Esta relación tiene la propiedad única de que, cuando se corta o se dobla por la mitad a lo ancho, las mitades también tienen la misma relación de aspecto. Cada tamaño de papel ISO es la mitad del área del siguiente tamaño más grande de la misma serie. [1]
Dimensiones de las series A, B y C
| Tamaño | Formatos de serie A | Formatos de la serie B | Formatos de la serie C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| nombre | mm | pulgadas | nombre | mm | pulgadas | nombre | mm | pulgadas | |
| -2 | 4A0 | 1682 × 2378 | 66,2 × 93,6 | ||||||
| -1 | 2A0 | 1189 × 1682 | 46,8 × 66,2 | ||||||
| 0 | A0 | 0 841 × 1189 | 33,1 × 46,8 | B0 | 1000 × 1414 | 39,4 × 55,7 | C0 | 0 917 × 1297 | 36,1 × 51,1 |
| 1 | A1 | 0 594 × 0 841 | 23,4 × 33,1 | B1 | 0 707 × 1000 | 27,8 × 39,4 | C1 | 0 648 × 0 917 | 25,5 × 36,1 |
| 2 | A2 | 0 420 × 0 594 | 16,5 × 23,4 | B2 | 0 500 × 0 707 | 19,7 × 27,8 | C2 | 0 458 × 0 648 | 18,0 × 25,5 |
| 3 | A3 | 0 297 × 0 420 | 11,7 × 16,5 | B3 | 0 353 × 0 500 | 13,9 × 19,7 | C3 | 0 324 × 0 458 | 12,8 × 18,0 |
| 4 | A4 | 0 210 × 0 297 | 0 8,3 × 11,7 | B4 | 0 250 × 0 353 | 0 9,8 × 13,9 | C4 | 0 229 × 0 324 | 0 9,0 × 12,8 |
| 5 | A5 | 0 148 × 0 210 | 0 5,8 × 0 8,3 | B5 | 0 176 × 0 250 | 0 6,9 × 0 9,8 | C5 | 0 162 × 0 229 | 0 6,4 × 0 9,0 |
| 6 | A6 | 0 105 × 0 148 | 0 4,1 × 0 5,8 | B6 | 0 125 × 0 176 | 0 4,9 × 0 6,9 | C6 | 0 114 × 0 162 | 0 4,5 × 0 6,4 |
| 7 | A7 | 0 0 74 × 0 105 | 0 2,9 × 0 4,1 | B7 | 0 0 88 × 0 125 | 0 3,5 × 0 4,9 | C7 | 0 0 81 × 0 114 | 0 3,2 × 0 4,5 |
| 8 | A8 | 0 0 52 × 0 0 74 | 0 2,0 × 0 2,9 | B8 | 0 0 62 × 0 0 88 | 0 2,4 × 0 3,5 | C8 | 0 0 57 × 0 0 81 | 0 2,2 × 0 3,2 |
| 9 | A9 | 0 0 37 × 0 0 52 | 0 1,5 × 0 2,0 | B9 | 0 0 44 × 0 0 62 | 0 1,7 × 0 2,4 | C9 | 0 0 40 × 0 0 57 | 0 1,6 × 0 2,2 |
| 10 | A10 | 0 0 26 × 0 0 37 | 0 1,0 × 0 1,5 | B10 | 0 0 31 × 0 0 44 | 0 1,2 × 0 1,7 | C10 | 0 0 28 × 0 0 40 | 0 1,1 × 0 1,6 |
 |  |  | |||||||

Historia
La mención más antigua conocida de las ventajas de basar un tamaño de papel en una relación de aspecto se encuentra en una carta escrita el 25 de octubre de 1786 por el científico alemán Georg Christoph Lichtenberg a Johann Beckmann , ambos en la Universidad de Göttingen . [2] Las primeras variantes de los formatos que se convertirían en tamaños de papel ISO A2, A3, B3, B4 y B5 evolucionaron luego en Francia, donde se enumeraron en una ley francesa de 1798 sobre impuestos a las publicaciones ( en francés : Loi sur le timbre (Nº 2136) ) que se basaba en parte en tamaños de página. [3]

En la búsqueda de un sistema estándar de formatos de papel con una base científica en la asociación Bridge ( en alemán : Die Brücke ), como reemplazo de la gran variedad de otros formatos de papel que se habían utilizado antes, con el fin de hacer que el almacenamiento de papel y la reproducción de documentos fueran más baratos y eficientes, en 1911 Wilhelm Ostwald propuso, más de cien años después de la ley francesa de 1798, [3] un estándar global - un formato mundial ( Weltformat ) - para tamaños de papel basado en la proporción , haciendo referencia al argumento presentado por la carta de Lichtenberg de 1786, pero vinculándolo al sistema métrico que usa 1 centímetro (0,39 pulgadas) como el ancho del formato base. Walter Porstmann argumentó en un largo artículo publicado en 1918, que una base firme para el sistema de formatos de papel, que tratan con superficies, no debería ser la longitud sino el área; es decir, vincular el sistema de formatos de papel al sistema métrico utilizando el metro cuadrado en lugar del centímetro, limitado por y área metro cuadrado, donde es la longitud del lado más corto y es la longitud del lado más largo, para la segunda ecuación ambas en metros. Porstmann también argumentó que los formatos para contenedores de papel, como sobres, deberían ser un 10% más grandes que el formato del papel en sí.
En 1921, después de una larga discusión y otra intervención de Porstmann, el Comité de Normalización de la Industria Alemana ( Normenausschuß der deutschen Industrie , o NADI en forma abreviada), que es el Instituto Alemán de Normalización ( Deutses Institut für Normung , o DIN en forma abreviada) publicó la norma alemana DI Norm 476 la especificación de cuatro series de formatos de papel con ratio , con la serie A como los formatos siempre preferidos y base para las otras series. Todas las medidas están redondeadas al milímetro más cercano. A0 tiene una superficie de 1 metro cuadrado (11 pies cuadrados) hasta un error de redondeo de , con un ancho de 841 milímetros (33,1 pulgadas) y una altura de 1.189 milímetros (46,8 pulgadas), por lo que un área real de 0,999949 metros cuadrados (10,76336 pies cuadrados); A4 se recomienda como tamaño de papel estándar para correspondencia comercial, administrativa y gubernamental; y A6 para postales. La serie B se basa en B0 con un ancho de 1 metro (3 pies 3 pulgadas), C0 tiene 917 por 1297 milímetros (36,1 pulgadas × 51,1 pulgadas) y D0 771 por 1090 milímetros (30,4 pulgadas × 42,9 pulgadas). La serie C es la base para los formatos de sobre.
El concepto de formato de papel DIN pronto se introdujo como estándar nacional en muchos otros países, por ejemplo, Bélgica (1924), Países Bajos (1925), Noruega (1926), Suiza (1929), Suecia (1930), Unión Soviética (1934), Hungría (1938), Italia (1939), Finlandia (1942), Uruguay (1942), Argentina (1943), Brasil (1943), España (1947), Austria (1948), Rumania (1949), Japón (1951), Dinamarca (1953), Checoslovaquia (1953), Israel (1954), Portugal (1954), Yugoslavia (1956), India (1957), Polonia (1957), Reino Unido (1959), Venezuela (1962), Nueva Zelanda (1963), Islandia (1964), México (1965), Sudáfrica (1966), Francia (1967), Perú (1968), Reino Unido (1970), Francia (1971), Italia (1972), Italia (1973), Italia (1974), Italia (1975), Italia (1976), Italia (1977), Italia (1978), Italia (1979), Italia (1980), Italia (1981), Italia (1982), Italia (1983), Italia (1984), Italia (1985), Italia (1986), Italia (1987), Italia (1988), Italia (1989), Italia (1990), Italia (1991), Italia (1992), Italia (1993), Italia (1994), Italia (1995), Italia (1996), Italia (1997), Italia (1998), Italia (1999), Italia (1999), Italia (1990), Italia (1991), Italia (1992), Italia (1993), Italia (1994), Italia (1995), Italia (199 (1967), Turquía (1967), Chile (1968), Grecia (1970), Zimbabwe (1970), Singapur (1970), Bangladesh (1972), Tailandia (1973), Barbados (1973), Australia (1974), Ecuador (1974), Colombia (1975) y Kuwait (1975).
Finalmente se convirtió en una norma internacional ( ISO 216) y en el formato oficial de documentos de las Naciones Unidas en 1975, y hoy en día se utiliza en casi todos los países del mundo, con excepción de varios países de las Américas.
En 1977, un gran fabricante de automóviles alemán realizó un estudio de los formatos de papel que encontraba en su correo entrante y concluyó que, de 148 países examinados, 88 ya utilizaban los formatos de la serie A. [4]
Ventajas
La principal ventaja de este sistema es su escalabilidad. El papel rectangular con una relación de aspecto de tiene la propiedad única de que, cuando se corta o se dobla por la mitad a la mitad entre sus lados más largos, cada mitad tiene la misma relación de aspecto que la hoja completa antes de ser dividida. De manera equivalente, si uno coloca dos hojas de papel del mismo tamaño con una relación de aspecto de una al lado de la otra a lo largo de su lado más largo, forman un rectángulo más grande con una relación de aspecto de y el doble del área de cada hoja individual.
El sistema ISO de tamaños de papel explota estas propiedades de la relación de aspecto. En cada serie de tamaños (por ejemplo, la serie A), el tamaño más grande se numera con el número 0 (en este caso, A0), y cada tamaño sucesivo (A1, A2, etc.) tiene la mitad del área de la hoja anterior y se puede cortar dividiendo por la mitad la longitud de la hoja del tamaño anterior. La nueva medida se redondea hacia abajo [ contradictorio ] al milímetro más cercano. Se puede hacer un folleto plegado utilizando una hoja del tamaño inmediatamente superior (por ejemplo, una hoja A4 se dobla por la mitad para hacer un folleto con páginas de tamaño A5). Se puede diseñar una fotocopiadora o impresora de oficina para reducir una página de A4 a A5 o para ampliar una página de A4 a A3. De manera similar, se pueden reducir dos hojas de A4 para que quepan en una hoja A4 sin exceso de papel vacío.
Este sistema también simplifica el cálculo del peso del papel. Según la norma ISO 536, el gramaje del papel se define como la masa de una hoja en gramos (g) por área en metros cuadrados (símbolo de unidad g/m2 ; también se utiliza la abreviatura no estándar "gsm"). [5] Se puede derivar el gramaje de otros tamaños mediante división aritmética . Una hoja estándar A4 hecha de papel de 80 g/m2 pesa 5 gramos (0,18 oz), ya que es 1 ⁄ 16 (cuatro mitades, ignorando el redondeo) de una página A0. Por lo tanto, el peso y la tarifa postal asociada se pueden aproximar fácilmente contando el número de hojas utilizadas.
La ISO 216 y sus normas relacionadas se publicaron por primera vez entre 1975 y 1995:
- ISO 216:2007, que define las series A y B de tamaños de papel
- ISO 269:1985, que define la serie C para sobres
- ISO 217:2013, que define las series RA y SRA de tamaños de papel en bruto ("sin recortar")
Propiedades
Una serie
El papel de la serie A tiene una relación de aspecto de √ 2 (≈ 1,414, cuando se redondea). A0 se define de modo que tenga un área de 1 m 2 (11 pies cuadrados ) antes de redondear al milímetro más cercano (0,039 pulgadas). Los tamaños de papel sucesivos de la serie (A1, A2, A3, etc.) se definen dividiendo a la mitad el área del tamaño de papel anterior y redondeando hacia abajo, de modo que el lado largo de A( n + 1) tenga la misma longitud que el lado corto de A n . Por lo tanto, cada tamaño siguiente tiene casi exactamente la mitad del área del tamaño anterior. Por lo tanto, una página A1 puede contener dos páginas A2 dentro de la misma área.
El tamaño más utilizado de esta serie es el A4, que mide 210 mm × 297 mm (8,27 in × 11,7 in) y, por lo tanto, tiene una superficie de casi exactamente 1 ⁄ 16 metros cuadrados (0,0625 m 2 ; 96,8752 in²). A modo de comparación, el tamaño de papel carta que se utiliza habitualmente en Norteamérica ( 8+1 ⁄ 2 in × 11 in; 216 mm × 279 mm) es aproximadamente 6 mm ( 0,24 in ) más ancho y 18 mm ( 0,71 in ) más corto que el A4. Entonces, el tamaño del papel A5 es la mitad del A4, es decir, 148 mm × 210 mm ( 5,8 in × 8,3 in ). [6] [7]
La razón geométrica para utilizar la raíz cuadrada de 2 es mantener la relación de aspecto de cada rectángulo posterior después de cortar o doblar una hoja de la serie A por la mitad, perpendicular al lado más grande. Dado un rectángulo con un lado más largo, x , y un lado más corto, y , garantizar que su relación de aspecto, incógnita/y , será igual que la de un rectángulo de la mitad de su tamaño, y/x /2 , lo que significa que incógnita/y = y/x /2 , lo que se reduce a incógnita/y = √ 2 ; en otras palabras, una relación de aspecto de 1: √ 2 .
Cualquier papel A n se puede definir como A n = S × L , donde (medido en metros)
Por lo tanto
- , Etc.
Serie B
La serie B se define en la norma de la siguiente manera: "Una serie subsidiaria de tamaños se obtiene colocando las medias geométricas entre tamaños adyacentes de la serie A en secuencia". El uso de la media geométrica hace que cada paso en el tamaño: B0, A0, B1, A1, B2 ... sea más pequeño que el anterior por el mismo factor. Al igual que con la serie A, las longitudes de la serie B tienen la relación √ 2 , y doblando una por la mitad (y redondeando hacia abajo al milímetro más cercano) se obtiene la siguiente en la serie. El lado más corto de B0 es exactamente 1 metro.
También existe una serie B japonesa incompatible que, según la definición de JIS , tiene 1,5 veces el área de la serie A correspondiente de JIS (que es idéntica a la serie A de ISO). [8] Por lo tanto, las longitudes del papel de la serie B de JIS son √ 1,5 ≈ 1,22 veces las del papel de la serie A. En comparación, las longitudes del papel de la serie B de ISO son 4 √ 2 ≈ 1,19 veces las del papel de la serie A.
Cualquier papel B n (según la norma ISO) se puede definir como B n = S × L , donde (medido en metros)
Por lo tanto
- , Etc.
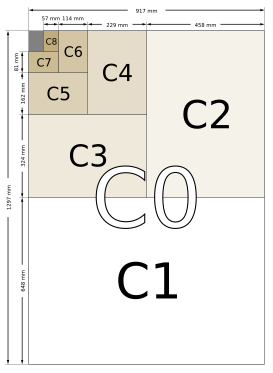
Serie C
Los formatos de la serie C son medias geométricas entre los formatos de la serie B y la serie A con el mismo número (por ejemplo, C2 es la media geométrica entre B2 y A2). La relación entre el ancho y la altura de los formatos de la serie C es √ 2, como en las series A y B. Las series de papel A, B y C encajan entre sí como parte de una progresión geométrica , con una relación de longitudes de lados sucesivos de 8 √ 2 , aunque no hay un tamaño intermedio entre B n y A( n − 1) : A4, C4, B4, "D4", A3, ...; existe una serie D de este tipo en las extensiones suecas del sistema. Por lo tanto, las longitudes del papel de la serie C de ISO son 8 √ 2 ≈ 1,09 veces las del papel de la serie A.
Los formatos de la serie C se utilizan principalmente para sobres . Una página A4 sin doblar entrará en un sobre C4. Debido a la misma relación entre el ancho y la altura, si una página A4 se dobla por la mitad para que tenga un tamaño A5, entrará en un sobre C5 (que tendrá el mismo tamaño que un sobre C4 doblado por la mitad).
Cualquier papel C n se puede definir como C n = S × L , donde (medido en metros)
Por lo tanto
- , Etc.
Tolerancias
Las tolerancias especificadas en la norma son:
- ± 1,5 mm para dimensiones de hasta 150 mm,
- ±2,0 mm para dimensiones en el rango de 150 a 600 mm, y
- ±3,0 mm para dimensiones superiores a 600 mm.
Estos están relacionados con la comparación entre las series A, B y C.
Solicitud
Los formatos ISO 216 se organizan en torno a la proporción 1: √ 2 ; dos hojas juntas tienen la misma proporción, de lado a lado. En la fotocopia a escala, por ejemplo, dos hojas A4 reducidas a tamaño A5 caben exactamente en una hoja A4, y una hoja A4 en tamaño ampliado en una hoja A3; en cada caso, no hay desperdicio ni escasez.
Los principales países que no suelen utilizar los tamaños de papel ISO son Estados Unidos y Canadá, que utilizan tamaños de papel norteamericanos . Aunque también han adoptado oficialmente el formato de papel ISO 216, México, Panamá, Perú, Colombia, Filipinas y Chile también utilizan mayoritariamente tamaños de papel estadounidenses.
Las hojas de papel rectangulares con una proporción de 1: √ 2 son populares en el plegado de papel , como el origami , donde a veces se las llama "rectángulos A4" o "rectángulos plateados". [9] En otros contextos, el término "rectángulo plateado" también puede referirse a un rectángulo en la proporción 1: (1 + √ 2 ), conocida como la proporción de plata .
Anchos de bolígrafo técnicos compatibles

Un complemento a los tamaños de papel ISO, en particular la serie A, son los anchos de línea de dibujo técnico especificados en la norma ISO 128. Por ejemplo, el tipo de línea A ("Continua - gruesa", utilizada para "contornos visibles") tiene un grosor estándar de 0,7 mm en una hoja de tamaño A0, 0,5 mm en una hoja A1 y 0,35 mm en A2, A3 o A4. [10]
Los anchos de pluma técnica que se corresponden son 0,13, 0,18, 0,25, 0,35, 0,5, 0,7, 1,0, 1,40 y 2,0 mm, tal como se especifica en la norma ISO 9175-1. Se asignan códigos de color a cada tamaño para facilitar su reconocimiento por parte del dibujante. Al igual que los tamaños de papel, estos anchos de pluma aumentan en un factor de √ 2 , de modo que se pueden utilizar plumas particulares en tamaños de papel particulares, y luego se puede utilizar el siguiente tamaño más pequeño o más grande para continuar el dibujo después de que se haya reducido o ampliado, respectivamente. [4] [11]
Ancho de línea (mm) 0,10 0,13 0,18 0,25 0,35 0,50 0,70 1.0 1.4 2.0 Color Granate Violeta Rojo Blanco Amarillo Marrón Azul Naranja Verde Gris

La norma anterior DIN 6775 en la que se basa la ISO 9175-1 también especificaba un término y un símbolo para una fácil identificación de lápices y plantillas de dibujo compatibles con la norma, llamados Micronorm , que todavía pueden encontrarse en algunos equipos de dibujo técnico.
Sobreformatos
La norma DIN 476 prevé formatos mayores que A0, que se indican mediante un factor de prefijo. En particular, enumera los formatos 2A0 y 4A0, que son el doble y el cuádruple del tamaño de A0 respectivamente:
| Nombre | mm × mm | pulgada × pulgada |
|---|---|---|
| 4A0 | 1682 × 2378 | 66+5 ⁄ 24 × 93+5 ⁄ 8 |
| 2A0 | 1189 × 1682 | 46+19 ⁄ 24 × 66+5 ⁄ 24 |
Aunque no están definidos formalmente, la norma ISO 216:2007 también los menciona en la tabla de Series principales de tamaños recortados (serie ISO A): "Los tamaños raramente utilizados [2A0 y 4A0] que siguen también pertenecen a esta serie". El 2A0 también se conoce con otros nombres no oficiales como "A00". [12]
Véase también
Referencias
- ^ "Tamaños y formatos de papel internacionales". Tamaños de papel . Consultado el 29 de junio de 2020 .
- ↑ Lichtenberg, Georg Christoph (7 de febrero de 2006) [Escrito el 25 de octubre de 1786]. «Lichtenberg's letter to Johann Beckmann» (en alemán e inglés). Traducido por Kuhn, Markus . Universidad de Cambridge . Consultado el 10 de mayo de 2016 .Publicado en Lichtenberg, Georg Christoph (1990). Joost, Ulrich; Schöne, Albrecht (eds.). Briefwechsel [ Correspondencia ] (en alemán). vol. III (1785-1792). Múnich: Beck. págs. 274–75. ISBN 3-406-30958-5. Recuperado el 10 de mayo de 2016 .
- ^ ab "Loi sur le timbre (Nº 2136)" [Ley de Sellos (Nº 2136)]. Bulletin des Lois de la République (en francés) (237). París: República de Francia: 1–2. 3 de noviembre de 1798. Archivado desde el original el 26 de abril de 2009 . Consultado el 20 de enero de 2024 a través de Markus Kuhn.
- ^ ab Kuhn, Markus. «Tamaños de papel estándar internacionales» . Consultado el 30 de agosto de 2017 .
- ^ Organización Internacional de Normalización (noviembre de 2019). «ISO 536:2019(en): Papel y cartón — Determinación del gramaje». Plataforma de navegación ISO (4.ª ed.). § 3.1 nota 1. Consultado el 8 de junio de 2021 .
- ^ "Tamaños de papel A: A0, A1, A2, A3, A4, A5, A6, A7, A8, A9". papersizes.org . Consultado el 2 de agosto de 2018 .
- ^ "Tamaños, dimensiones, formatos y estándares de papel internacionales". PaperSize . Consultado el 5 de octubre de 2018 .
- ^ "Tamaño de papel de la serie B japonesa" . Consultado el 18 de abril de 2010 .
- ^ Lister, David. "El rectángulo A4". The Lister List . Inglaterra: British Origami Society . Consultado el 6 de mayo de 2009 .
- ^ Bell, Steven. "Tamaños de pluma y tipos de línea". Metrication.com . Consultado el 30 de agosto de 2017 .
- ^ "Tamaños de lápiz para dibujo técnico". Wiki de Designing Buildings . Consultado el 30 de agosto de 2017 .
- ^ "A00".
Enlaces externos
- Tamaños de papel estándar internacionales: detalles y fundamentos de la norma ISO 216
- ISO 216 en iso.org
- Artículos de Wilhelm Ostwald que hacen referencia a la carta de Lichtenberg y de W. Porstmann que especifica un sistema métrico de normas para formatos de longitudes, superficies (planos) y volúmenes, sentando las bases para la serie DIN, en alemán
- Explicación de los tamaños de papel


















