Recristalización (metalurgia)

Cristalización
Fundamentos
Cristal Estructura cristalina Nucleación
Conceptos
Cristalización Crecimiento de cristales Recristalización Cristal semilla Protocristalino Cristal único
Métodos y tecnología
Petanca Método de Bridgman-Stockbarger Proceso de Van Arkel-de Boer Método Czochralski Epitaxia Método de flujo Cristalización fraccionada Congelación fraccionada Síntesis hidrotermal El método de Kyropoulos Crecimiento del pedestal calentado por láser Micro-tirón hacia abajo Procesos de modelado en el crecimiento de cristales. Crisol de calavera Método Verneuil Zona de fusión
en a mi

En la ciencia de los materiales , la recristalización es un proceso por el cual los granos deformados son reemplazados por un nuevo conjunto de granos libres de defectos que se nuclean y crecen hasta que los granos originales se han consumido por completo. La recristalización suele ir acompañada de una reducción de la resistencia y dureza de un material y un aumento simultáneo de la ductilidad . Por lo tanto, el proceso puede introducirse como un paso deliberado en el procesamiento de metales o puede ser un subproducto indeseable de otro paso de procesamiento. Los usos industriales más importantes son el ablandamiento de metales previamente endurecidos o quebradizos por trabajo en frío y el control de la estructura del grano en el producto final. La temperatura de recristalización suele ser de 0,3 a 0,4 veces el punto de fusión para metales puros y de 0,5 veces para aleaciones.

La recristalización se define como el proceso en el cual los granos de una estructura cristalina adquieren una nueva estructura o una nueva forma cristalina.

Es difícil dar una definición precisa de recristalización, ya que el proceso está estrechamente relacionado con otros procesos, en particular la recuperación y el crecimiento del grano . En algunos casos, es difícil definir con precisión el punto en el que comienza un proceso y termina otro. Doherty et al. definieron la recristalización como:

"... la formación de una nueva estructura de grano en un material deformado mediante la formación y migración de límites de grano de ángulo alto impulsados ​​por la energía de deformación almacenada. Los límites de grano de ángulo alto son aquellos con una desorientación mayor a 10-15°" ^[1]

Por lo tanto, el proceso puede diferenciarse de la recuperación (donde los límites de grano de alto ángulo no migran) y el crecimiento de grano (donde la fuerza impulsora solo se debe a la reducción del área límite). La recristalización puede ocurrir durante o después de la deformación (durante el enfriamiento o el tratamiento térmico posterior, por ejemplo). La primera se denomina dinámica, mientras que la segunda se denomina estática . Además, la recristalización puede ocurrir de manera discontinua, donde se forman y crecen nuevos granos distintos, o de manera continua, donde la microestructura evoluciona gradualmente hacia una microestructura recristalizada. Los diferentes mecanismos por los que ocurren la recristalización y la recuperación son complejos y en muchos casos siguen siendo controvertidos. La siguiente descripción es principalmente aplicable a la recristalización discontinua estática, que es la variedad más clásica y probablemente la más entendida. Los mecanismos adicionales incluyen la recristalización dinámica ( geométrica ) y la migración de límites inducida por deformación.

La recristalización secundaria ocurre cuando una cantidad muy pequeña de granos {110}<001> (Goss) crece selectivamente, aproximadamente uno en 106 granos primarios, a expensas de muchos otros granos primarios recristalizados. Esto da como resultado un crecimiento anormal del grano , que puede ser beneficioso o perjudicial para las propiedades del material del producto. El mecanismo de recristalización secundaria es un tamaño de grano primario pequeño y uniforme, logrado a través de la inhibición del crecimiento normal del grano por precipitados finos llamados inhibidores. ^[2] Los granos Goss reciben su nombre en honor a Norman P. Goss , el inventor del acero eléctrico de grano orientado alrededor de 1934.

Existen varias leyes de recristalización, en gran medida empíricas:

• Activación térmica . La velocidad de los mecanismos microscópicos que controlan la nucleación y el crecimiento de los granos recristalizados depende de la temperatura de recocido. Las ecuaciones de tipo Arrhenius indican una relación exponencial.
• Temperatura crítica . Siguiendo la regla anterior se encuentra que la recristalización requiere una temperatura mínima para que se produzcan los mecanismos atómicos necesarios. Esta temperatura de recristalización disminuye con el tiempo de recocido.
• Deformación crítica . La deformación previa aplicada al material debe ser adecuada para proporcionar núcleos y suficiente energía almacenada para impulsar su crecimiento.
• La deformación afecta la temperatura crítica . Aumentar la magnitud de la deformación previa o reducir la temperatura de deformación aumentará la energía almacenada y el número de núcleos potenciales. Como resultado, la temperatura de recristalización disminuirá con el aumento de la deformación.
• El tamaño inicial del grano afecta la temperatura crítica . Los límites de grano son buenos sitios para la formación de núcleos. Dado que un aumento en el tamaño del grano da como resultado menos límites, esto produce una disminución en la tasa de nucleación y, por lo tanto, un aumento en la temperatura de recristalización.
• La deformación afecta el tamaño final del grano . Aumentar la deformación o reducir la temperatura de deformación aumenta la tasa de nucleación más rápido que la tasa de crecimiento. Como resultado, el tamaño final del grano se reduce debido al aumento de la deformación.

Durante la deformación plástica, el trabajo realizado es la integral de la tensión y la deformación en el régimen de deformación plástica. Aunque la mayor parte de este trabajo se convierte en calor, una fracción (~1–5%) se retiene en el material en forma de defectos, en particular dislocaciones. La reorganización o eliminación de estas dislocaciones reducirá la energía interna del sistema, por lo que existe una fuerza impulsora termodinámica para tales procesos. A temperaturas moderadas a altas, en particular en materiales con una alta energía de falla de apilamiento, como el aluminio y el níquel, la recuperación se produce fácilmente y las dislocaciones libres se reorganizarán fácilmente en subgranos rodeados de límites de grano de ángulo bajo. La fuerza impulsora es la diferencia de energía entre el estado deformado y el recristalizado Δ E , que puede determinarse mediante la densidad de dislocaciones o el tamaño del subgrano y la energía límite (Doherty, 2005):

${\displaystyle \Delta \ E\approx \;\rho \;Gb^{2}\;{\rm {o}}\;\approx \;3\gamma _{s}/d_{s}\,\!}$

donde ρ es la densidad de dislocaciones, G es el módulo de corte, b es el vector de Burgers de las dislocaciones, γ _s es la energía del límite del subgrano y d _s es el tamaño del subgrano.

Históricamente se suponía que la tasa de nucleación de nuevos granos recristalizados estaría determinada por el modelo de fluctuación térmica utilizado con éxito para los fenómenos de solidificación y precipitación . En esta teoría se supone que como resultado del movimiento natural de los átomos (que aumenta con la temperatura) surgirían espontáneamente pequeños núcleos en la matriz. La formación de estos núcleos estaría asociada a un requerimiento de energía debido a la formación de una nueva interfaz y una liberación de energía debido a la formación de un nuevo volumen de material de menor energía. Si los núcleos fueran más grandes que un radio crítico, entonces serían termodinámicamente estables y podrían comenzar a crecer. El principal problema con esta teoría es que la energía almacenada debido a las dislocaciones es muy baja (0,1–1 J m ⁻³ ) mientras que la energía de un límite de grano es bastante alta (~0,5 J m ⁻³ ). Los cálculos basados ​​en estos valores encontraron que la tasa de nucleación observada era mayor que la calculada por un factor imposiblemente grande (~10 ⁵⁰ ).

Como resultado, la teoría alternativa propuesta por Cahn en 1949 es ahora universalmente aceptada. Los granos recristalizados no se nuclean de la manera clásica, sino que crecen a partir de subgranos y células preexistentes. El "tiempo de incubación" es entonces un período de recuperación donde los subgranos con límites de ángulo bajo (<1–2°) comienzan a acumular dislocaciones y se desorientan cada vez más con respecto a sus vecinos. El aumento de la desorientación aumenta la movilidad del límite y, por lo tanto, aumenta la tasa de crecimiento del subgrano. Si un subgrano en un área local tiene una ventaja sobre sus vecinos (como densidades de dislocaciones localmente altas, un mayor tamaño u orientación favorable), entonces este subgrano podrá crecer más rápidamente que sus competidores. A medida que crece, su límite se desorienta cada vez más con respecto al material circundante hasta que puede reconocerse como un grano completamente nuevo y libre de tensiones.

Se observa comúnmente que la cinética de recristalización sigue el perfil que se muestra. Existe un "período de nucleación" inicial t ₀ en el que se forman los núcleos y luego comienzan a crecer a un ritmo constante consumiendo la matriz deformada. Aunque el proceso no sigue estrictamente la teoría clásica de nucleación, a menudo se encuentra que tales descripciones matemáticas brindan al menos una aproximación cercana. Para una matriz de granos esféricos, el radio medio R en un momento t es (Humphreys y Hatherly 2004):

${\displaystyle R=G\left(t-t_{0}\right)\,\!}$

donde t ₀ es el tiempo de nucleación y G es la tasa de crecimiento dR/dt. Si se forman N núcleos en el incremento de tiempo dt y se supone que los granos son esféricos, entonces la fracción de volumen será:

${\displaystyle f={\frac {4}{3}}\pi \ {\dot {N}}G^{3}\int _{0}^{t}(t-t_{0})^{3}\,dt={\frac {\pi \ }{3}}{\dot {N}}G^{3}t^{4}\,\!}$

Esta ecuación es válida en las primeras etapas de la recristalización cuando f<<1 y los granos en crecimiento no chocan entre sí. Una vez que los granos entran en contacto, la velocidad de crecimiento se reduce y está relacionada con la fracción de material no transformado (1-f) mediante la ecuación de Johnson-Mehl:

${\displaystyle f=1-\exp \left(-{\frac {\pi \ }{3}}{\dot {N}}G^{3}t^{4}\right)\,\!}$

Si bien esta ecuación proporciona una mejor descripción del proceso, aún supone que los granos son esféricos, las tasas de nucleación y crecimiento son constantes, los núcleos están distribuidos aleatoriamente y el tiempo de nucleación t ₀ es pequeño. En la práctica, pocos de estos modelos son realmente válidos y es necesario utilizar modelos alternativos.

En general, se reconoce que cualquier modelo útil no sólo debe tener en cuenta la condición inicial del material, sino también la relación en constante cambio entre los granos en crecimiento, la matriz deformada y cualquier segunda fase u otros factores microestructurales. La situación se complica aún más en sistemas dinámicos en los que la deformación y la recristalización se producen simultáneamente. Como resultado, en general ha resultado imposible producir un modelo predictivo preciso para procesos industriales sin recurrir a pruebas empíricas exhaustivas. Dado que esto puede requerir el uso de equipos industriales que no se han construido realmente, este enfoque presenta claras dificultades.

La temperatura de recocido tiene una influencia importante en la velocidad de recristalización, lo que se refleja en las ecuaciones anteriores. Sin embargo, para una temperatura determinada, existen varios factores adicionales que influirán en la velocidad.

La velocidad de recristalización está fuertemente influenciada por la cantidad de deformación y, en menor medida, la forma en que se aplica. Los materiales muy deformados recristalizarán más rápidamente que los deformados en menor medida. De hecho, por debajo de una cierta deformación, la recristalización puede no ocurrir nunca. La deformación a temperaturas más altas permitirá la recuperación concurrente y, por lo tanto, dichos materiales recristalizarán más lentamente que los deformados a temperatura ambiente, por ejemplo, contrasta el laminado en caliente y en frío . En ciertos casos, la deformación puede ser inusualmente homogénea o ocurrir solo en planos cristalográficos específicos . La ausencia de gradientes de orientación y otras heterogeneidades puede impedir la formación de núcleos viables. Los experimentos en la década de 1970 encontraron que el molibdeno se deformaba a una deformación real de 0,3, recristalizaba más rápidamente cuando se tensaba y a velocidades decrecientes para el trefilado , el laminado y la compresión (Barto y Ebert 1971).

La orientación de un grano y la forma en que cambia durante la deformación influyen en la acumulación de energía almacenada y, por lo tanto, en la velocidad de recristalización. La movilidad de los límites de grano está influenciada por su orientación, por lo que algunas texturas cristalográficas darán lugar a un crecimiento más rápido que otras.

Los átomos de soluto, tanto las adiciones deliberadas como las impurezas, tienen una profunda influencia en la cinética de recristalización. Incluso concentraciones menores pueden tener una influencia sustancial; por ejemplo, un 0,004 % de Fe aumenta la temperatura de recristalización en alrededor de 100 °C (Humphreys y Hatherly 2004). Actualmente se desconoce si este efecto se debe principalmente al retraso de la nucleación o a la reducción de la movilidad de los límites de grano, es decir, al crecimiento.

Muchas aleaciones de importancia industrial tienen una fracción de volumen de partículas de segunda fase, ya sea como resultado de impurezas o de adiciones deliberadas de aleación. Dependiendo de su tamaño y distribución, dichas partículas pueden actuar para estimular o retardar la recristalización.

La recristalización se evita o se ralentiza significativamente mediante una dispersión de partículas pequeñas y muy espaciadas debido a la fijación Zener en los límites de grano de ángulos altos y bajos. Esta presión se opone directamente a la fuerza impulsora que surge de la densidad de dislocación e influirá tanto en la cinética de nucleación como en la de crecimiento. El efecto se puede racionalizar con respecto al nivel de dispersión de partículas , donde es la fracción de volumen de la segunda fase y r es el radio. En un nivel bajo, el tamaño de grano está determinado por el número de núcleos, por lo que inicialmente puede ser muy pequeño. Sin embargo, los granos son inestables con respecto al crecimiento del grano y, por lo tanto, crecerán durante el recocido hasta que las partículas ejerzan suficiente presión de fijación para detenerlos. En un nivel moderado, el tamaño de grano todavía está determinado por el número de núcleos, pero ahora los granos son estables con respecto al crecimiento normal (mientras que el crecimiento anormal todavía es posible). En un nivel alto, la estructura deformada no recristalizada es estable y se suprime la recristalización.$Estilo de visualización F_{v}/r$$Estilo de visualización F_{v}$$Estilo de visualización F_{v}/r$$Estilo de visualización F_{v}/r$$Estilo de visualización F_{v}/r$

Los campos de deformación que rodean partículas grandes (superiores a 1 μm) no deformables se caracterizan por altas densidades de dislocación y grandes gradientes de orientación, por lo que son sitios ideales para el desarrollo de núcleos de recristalización. Este fenómeno, llamado nucleación estimulada por partículas (PSN), es notable porque proporciona una de las pocas formas de controlar la recristalización mediante el control de la distribución de partículas.

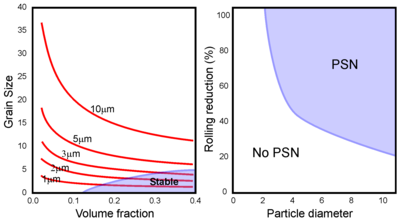
El tamaño y la desorientación de la zona deformada están relacionados con el tamaño de la partícula, por lo que se requiere un tamaño mínimo de partícula para iniciar la nucleación. Aumentar el grado de deformación reducirá el tamaño mínimo de partícula, lo que conducirá a un régimen PSN en el espacio de tamaño-deformación. Si la eficiencia de PSN es uno (es decir, cada partícula estimula un núcleo), entonces el tamaño de grano final estará determinado simplemente por la cantidad de partículas. Ocasionalmente, la eficiencia puede ser mayor que uno si se forman múltiples núcleos en cada partícula, pero esto es poco común. La eficiencia será menor que uno si las partículas están cerca del tamaño crítico y las fracciones grandes de partículas pequeñas en realidad evitarán la recristalización en lugar de iniciarla (ver arriba).

El comportamiento de recristalización de materiales que contienen una amplia distribución de tamaños de partículas puede ser difícil de predecir. Esto se agrava en aleaciones donde las partículas son inestables térmicamente y pueden crecer o disolverse con el tiempo. En varios sistemas, puede ocurrir un crecimiento anormal del grano dando lugar a cristales inusualmente grandes que crecen a expensas de los más pequeños. La situación es más simple en aleaciones bimodales que tienen dos poblaciones de partículas distintas. Un ejemplo son las aleaciones de Al-Si donde se ha demostrado que incluso en presencia de partículas muy grandes (<5 μm) el comportamiento de recristalización está dominado por las partículas pequeñas (Chan y Humphreys 1984). En tales casos, la microestructura resultante tiende a parecerse a la de una aleación con solo partículas pequeñas.

La temperatura de recristalización es la temperatura a la que puede producirse la recristalización para un material y unas condiciones de procesamiento determinados. No es una temperatura fija y depende de factores como los siguientes: ^[3]

• Aumentar el tiempo de recocido disminuye la temperatura de recristalización.
• Las aleaciones tienen temperaturas de recristalización más altas que los metales puros.
• Aumentar la cantidad de trabajo en frío disminuye la temperatura de recristalización.
• Los tamaños de grano más pequeños trabajados en frío disminuyen la temperatura de recristalización.

Temperaturas de recristalización habituales en metales seleccionados ^[4]

Metal	Temperatura de recristalización ( )${\displaystyle ^{\circ }\mathrm {C} }$	Temperatura de fusión ( )${\displaystyle ^{\circ }\mathrm {C} }$
Pb	99	327
Alabama	198	660
Mg	195	650
Cu	326	1085
Fé	462	1538
Yo	1024	3410

• Diagrama de fases

• RL Barto; LJ Ebert (1971). "Efectos del estado de tensión de deformación en la cinética de recristalización del molibdeno". Metallurgical Transactions . 2 (6): 1643–1649. Bibcode :1971MT......2.1643B. doi :10.1007/BF02913888. S2CID  136433819.
• HM Chan; FJ Humphreys (1984). "La recristalización de aleaciones de aluminio y silicio que contienen una distribución de partículas bimodal". Acta Metallurgica . 32 (2): 235–243. doi :10.1016/0001-6160(84)90052-X.
• RD Doherty (2005). "Recristalización primaria". En RW Cahn; et al. (eds.). Enciclopedia de materiales: ciencia y tecnología . Elsevier. págs. 7847–7850.
• RD Doherty; DA Hughes; FJ Humphreys; JJ Jonas; D Juul Jenson; ME Kassner; WE King; TR McNelley; HJ McQueen; AD Rollett (1997). "Cuestiones actuales en recristalización: una revisión". Ciencia e ingeniería de materiales . A238 : 219–274.
• FJ Humphreys; M Hatherly (2004). Recristalización y fenómenos de recocido relacionados . Elsevier.