Corriente alterna

En un circuito eléctrico, la potencia instantánea es la velocidad temporal del flujo de energía que pasa por un punto determinado del circuito. En los circuitos de corriente alterna , los elementos de almacenamiento de energía, como inductores y condensadores, pueden provocar inversiones periódicas de la dirección del flujo de energía. Su unidad en el SI es el vatio .
La parte de potencia instantánea que, promediada durante un ciclo completo de la forma de onda de CA , da como resultado una transferencia neta de energía en una dirección se conoce como potencia activa instantánea, y su promedio temporal se conoce como potencia activa o potencia real . [1] : 3 La parte de potencia instantánea que no da como resultado una transferencia neta de energía sino que oscila entre la fuente y la carga en cada ciclo debido a la energía almacenada se conoce como potencia reactiva instantánea, y su amplitud es el valor absoluto de la potencia reactiva . [2] [1] : 4
Potencia activa, reactiva, aparente y compleja en estado estable sinusoidal
En un circuito de corriente alterna (CA) simple que consta de una fuente y una carga lineal invariante en el tiempo , tanto la corriente como el voltaje son sinusoidales a la misma frecuencia. [3] Si la carga es puramente resistiva , las dos cantidades invierten su polaridad al mismo tiempo. Por lo tanto, la potencia instantánea, dada por el producto del voltaje y la corriente, es siempre positiva, de modo que la dirección del flujo de energía no se invierte y siempre es hacia la resistencia. En este caso, solo se transfiere potencia activa.
Si la carga es puramente reactiva , entonces el voltaje y la corriente están desfasados 90 grados. Durante dos cuartos de cada ciclo, el producto del voltaje y la corriente es positivo, pero durante los otros dos cuartos, el producto es negativo, lo que indica que, en promedio, fluye hacia la carga exactamente la misma cantidad de energía que la que sale. No hay un flujo neto de energía durante cada medio ciclo. En este caso, solo fluye potencia reactiva: no hay transferencia neta de energía a la carga; sin embargo, la potencia eléctrica fluye a lo largo de los cables y regresa fluyendo en sentido inverso a lo largo de los mismos cables. La corriente requerida para este flujo de potencia reactiva disipa energía en la resistencia de la línea, incluso si el dispositivo de carga ideal no consume energía por sí mismo. Las cargas prácticas tienen resistencia además de inductancia o capacitancia, por lo que tanto la potencia activa como la reactiva fluirán hacia las cargas normales.
La potencia aparente es el producto de los valores RMS de voltaje y corriente. La potencia aparente se tiene en cuenta al diseñar y operar sistemas de potencia, porque aunque la corriente asociada con la potencia reactiva no realiza trabajo en la carga, aún debe ser suministrada por la fuente de potencia. Los conductores, transformadores y generadores deben dimensionarse para transportar la corriente total, no solo la corriente que realiza trabajo útil. Una potencia reactiva insuficiente puede reducir los niveles de voltaje en una red eléctrica y, bajo ciertas condiciones de operación, colapsar la red (un apagón ). Otra consecuencia es que sumar la potencia aparente de dos cargas no dará con precisión la potencia total a menos que tengan la misma diferencia de fase entre corriente y voltaje (el mismo factor de potencia ).
Convencionalmente, los capacitores se tratan como si generaran potencia reactiva, y los inductores como si la consumieran. Si un capacitor y un inductor se colocan en paralelo, las corrientes que fluyen a través del capacitor y el inductor tienden a cancelarse en lugar de sumarse. Este es el mecanismo fundamental para controlar el factor de potencia en la transmisión de energía eléctrica; los capacitores (o inductores) se insertan en un circuito para compensar parcialmente la potencia reactiva "consumida" ("generada") por la carga. Los circuitos puramente capacitivos suministran potencia reactiva con la forma de onda de corriente adelantada a la forma de onda de voltaje por 90 grados, mientras que los circuitos puramente inductivos absorben potencia reactiva con la forma de onda de corriente retrasada a la forma de onda de voltaje por 90 grados. El resultado de esto es que los elementos de circuito capacitivos e inductivos tienden a cancelarse entre sí. [4]
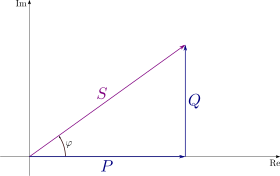
La potencia compleja es la suma vectorial de la potencia activa y reactiva. La potencia aparente es la magnitud de la potencia compleja.
Potencia activa , P
Potencia reactiva , Q
Potencia compleja , S
Potencia aparente , |S|
Fase del voltaje con respecto a la corriente ,
Los ingenieros utilizan los siguientes términos para describir el flujo de energía en un sistema (y asignan a cada uno de ellos una unidad diferente para diferenciarlos):
- Potencia activa , [5] P , o potencia real : [6] vatio (W);
- Potencia reactiva , Q : voltio-amperio reactivo (var);
- Potencia compleja , S : voltio-amperio (VA);
- Potencia aparente , | S |: la magnitud de la potencia compleja S : voltio-amperio (VA);
- Fase del voltaje con respecto a la corriente , φ : ángulo de diferencia (en grados) entre la corriente y el voltaje; voltaje de atraso de la corriente ( vector del cuadrante I), voltaje de adelanto de la corriente (vector del cuadrante IV).
Todos ellos se indican en el diagrama adyacente (llamado triángulo de potencia).
En el diagrama, P es la potencia activa, Q es la potencia reactiva (en este caso positiva), S es la potencia compleja y la longitud de S es la potencia aparente. La potencia reactiva no realiza ningún trabajo, por lo que se representa como el eje imaginario del diagrama vectorial. La potencia activa sí realiza trabajo, por lo que es el eje real.
La unidad de potencia es el vatio (símbolo: W). La potencia aparente se expresa a menudo en voltamperios (VA), ya que es el producto del voltaje RMS y la corriente RMS . La unidad de potencia reactiva es var, que significa voltamperio reactivo . Dado que la potencia reactiva no transfiere energía neta a la carga, a veces se la llama potencia "sin vatios". Sin embargo, cumple una función importante en las redes eléctricas y su falta se ha citado como un factor significativo en el apagón del noreste de EE . UU . de 2003. [7] Comprender la relación entre estas tres cantidades es fundamental para comprender la ingeniería eléctrica. La relación matemática entre ellas se puede representar mediante vectores o expresar utilizando números complejos , S = P + j Q (donde j es la unidad imaginaria ).

Cálculos y ecuaciones en estado estacionario sinusoidal
La fórmula para la potencia compleja (unidades: VA) en forma fasorial es:
- ,
donde V denota voltaje en forma fasorial, con la amplitud como RMS , e I denota corriente en forma fasorial, con la amplitud como RMS. También por convención, se utiliza el conjugado complejo de I , que se denota (o ), en lugar de I en sí. Esto se hace porque de lo contrario usar el producto VI para definir S daría como resultado una cantidad que depende del ángulo de referencia elegido para V o I, pero definir S como VI* da como resultado una cantidad que no depende del ángulo de referencia y permite relacionar S con P y Q. [8]
Otras formas de potencia compleja (unidades en voltios-amperios, VA) se derivan de Z , la impedancia de carga (unidades en ohmios, Ω).
- .
En consecuencia, con referencia al triángulo de potencia, la potencia real (unidades en vatios, W) se deriva como:
- .
Para una carga puramente resistiva, la potencia real se puede simplificar a:
- .
R denota resistencia (unidades en ohmios, Ω) de la carga.
La potencia reactiva (unidades en voltios-amperios-reactivos, var) se deriva como:
- .
Para una carga puramente reactiva, la potencia reactiva se puede simplificar a:
- ,
donde X denota reactancia (unidades en ohmios, Ω) de la carga.
Combinando, la potencia compleja (unidades en voltios-amperios, VA) se deriva de nuevo como
- ,
y la potencia aparente (unidades en voltios-amperios, VA) como
- .
Estos se simplifican esquemáticamente mediante el triángulo de potencia.
Factor de potencia
La relación entre la potencia activa y la potencia aparente en un circuito se denomina factor de potencia . Para dos sistemas que transmiten la misma cantidad de potencia activa, el sistema con el factor de potencia más bajo tendrá corrientes circulantes más altas debido a la energía que regresa a la fuente desde el almacenamiento de energía en la carga. Estas corrientes más altas producen mayores pérdidas y reducen la eficiencia general de transmisión. Un circuito con un factor de potencia más bajo tendrá una potencia aparente más alta y mayores pérdidas para la misma cantidad de potencia activa. El factor de potencia es 1,0 cuando el voltaje y la corriente están en fase . Es cero cuando la corriente se adelanta o se retrasa con respecto al voltaje en 90 grados. Cuando el voltaje y la corriente están desfasados 180 grados, el factor de potencia es negativo uno y la carga está alimentando energía a la fuente (un ejemplo sería una casa con células solares en el techo que alimentan la red eléctrica cuando brilla el sol). Los factores de potencia generalmente se expresan como "adelantados" o "atrasados" para mostrar el signo del ángulo de fase de la corriente con respecto al voltaje. El voltaje se designa como la base con la que se compara el ángulo de corriente, lo que significa que la corriente se considera como voltaje "adelantado" o "atrasado". Cuando las formas de onda son puramente sinusoidales, el factor de potencia es el coseno del ángulo de fase ( ) entre las formas de onda sinusoidales de corriente y voltaje. Las hojas de datos y las placas de identificación de los equipos a menudo abrevian el factor de potencia como " " por este motivo.
Ejemplo: La potencia activa es 700 W y el ángulo de fase entre la tensión y la corriente es 45,6°. El factor de potencia es cos(45,6°) = 0,700 . La potencia aparente es entonces: 700 W / cos(45,6°) = 1000 VA . El concepto de disipación de potencia en un circuito de CA se explica e ilustra con el ejemplo.
Por ejemplo, un factor de potencia de 0,68 significa que solo el 68 por ciento de la corriente total suministrada (en magnitud) está realmente realizando trabajo; la corriente restante no realiza trabajo en la carga. El factor de potencia es muy importante en las subestaciones del sector eléctrico. De la red nacional, se requiere que los subsectores tengan una cantidad mínima de factor de potencia. De lo contrario, hay muchas pérdidas. Principalmente, los requisitos varían entre 0,90 y 0,96 o más. Es mejor el factor de potencia, menos la pérdida.
Potencia reactiva
En un circuito de corriente continua, la potencia que fluye hacia la carga es proporcional al producto de la corriente que pasa por la carga y la caída de potencial a través de la carga. La potencia que se produce debido a un condensador o inductor se denomina potencia reactiva. Se produce debido a la naturaleza de CA de elementos como inductores y condensadores. La energía fluye en una dirección desde la fuente hasta la carga. En la energía de CA, tanto el voltaje como la corriente varían aproximadamente de forma sinusoidal. Cuando hay inductancia o capacitancia en el circuito, las formas de onda de voltaje y corriente no se alinean perfectamente. El flujo de potencia tiene dos componentes: un componente fluye desde la fuente hasta la carga y puede realizar trabajo en la carga; la otra parte, conocida como "potencia reactiva", se debe al retraso entre el voltaje y la corriente, conocido como ángulo de fase, y no puede realizar trabajo útil en la carga. Puede considerarse como una corriente que llega en el momento equivocado (demasiado tarde o demasiado pronto). Para distinguir la potencia reactiva de la potencia activa, se mide en unidades de " voltamperios reactivos " o var. Estas unidades se pueden simplificar a vatios, pero se dejan como var para indicar que no representan ninguna salida de trabajo real.
La energía almacenada en elementos capacitivos o inductivos de la red da lugar a un flujo de potencia reactiva. El flujo de potencia reactiva influye en gran medida en los niveles de tensión a través de la red. Los niveles de tensión y el flujo de potencia reactiva deben controlarse cuidadosamente para permitir que un sistema de energía funcione dentro de límites aceptables. Se utiliza una técnica conocida como compensación reactiva para reducir el flujo de potencia aparente a una carga reduciendo la potencia reactiva suministrada desde las líneas de transmisión y proporcionándola localmente. Por ejemplo, para compensar una carga inductiva, se instala un condensador de derivación cerca de la propia carga. Esto permite que toda la potencia reactiva que necesita la carga sea suministrada por el condensador y no tenga que transferirse a través de las líneas de transmisión. Esta práctica ahorra energía porque reduce la cantidad de energía que la empresa de servicios públicos debe producir para realizar la misma cantidad de trabajo. Además, permite diseños de líneas de transmisión más eficientes utilizando conductores más pequeños o menos conductores agrupados y optimizando el diseño de las torres de transmisión.
Cargas capacitivas vs. cargas inductivas
La energía almacenada en el campo magnético o eléctrico de un dispositivo de carga, como un motor o un condensador, provoca un desfase entre las formas de onda de la corriente y la tensión. Un condensador es un dispositivo que almacena energía en forma de campo eléctrico. A medida que la corriente pasa por el condensador, la acumulación de carga hace que se desarrolle una tensión opuesta a través del condensador. Esta tensión aumenta hasta un máximo determinado por la estructura del condensador. En una red de CA, la tensión a través de un condensador cambia constantemente. El condensador se opone a este cambio, lo que hace que la corriente se adelante a la tensión en fase. Se dice que los condensadores "generan" potencia reactiva y, por lo tanto, generan un factor de potencia adelantado.
Las máquinas de inducción son uno de los tipos de cargas más comunes en el sistema de energía eléctrica actual. Estas máquinas utilizan inductores o grandes bobinas de alambre para almacenar energía en forma de campo magnético. Cuando se aplica inicialmente un voltaje a la bobina, el inductor resiste fuertemente este cambio en la corriente y el campo magnético, lo que provoca un retraso en el tiempo para que la corriente alcance su valor máximo. Esto hace que la corriente se retrase con respecto al voltaje en fase. Se dice que los inductores "absorben" potencia reactiva y, por lo tanto, causan un factor de potencia rezagado. Los generadores de inducción pueden generar o absorber potencia reactiva y proporcionar una medida de control a los operadores del sistema sobre el flujo de potencia reactiva y, por lo tanto, el voltaje. [9] Debido a que estos dispositivos tienen efectos opuestos en el ángulo de fase entre el voltaje y la corriente, se pueden utilizar para "cancelar" los efectos de cada uno. Esto generalmente toma la forma de bancos de condensadores que se utilizan para contrarrestar el factor de potencia rezagado causado por los motores de inducción.
Control de potencia reactiva
Por lo general, se requiere que los generadores conectados a la transmisión respalden el flujo de potencia reactiva. Por ejemplo, en el sistema de transmisión del Reino Unido, los requisitos del Código de Red exigen que los generadores suministren su potencia nominal dentro de los límites de 0,85 de factor de potencia en retraso y 0,90 de factor de potencia en avance en los terminales designados. El operador del sistema realizará acciones de conmutación para mantener un perfil de voltaje seguro y económico mientras mantiene una ecuación de equilibrio de potencia reactiva:
La " ganancia del sistema " es una fuente importante de potencia reactiva en la ecuación de equilibrio de potencia anterior, que se genera por la naturaleza capacitiva de la propia red de transmisión. Al realizar acciones de conmutación decisivas a primera hora de la mañana, antes de que aumente la demanda, se puede maximizar la ganancia del sistema desde el principio, lo que ayuda a proteger el sistema durante todo el día. Para equilibrar la ecuación, será necesario el uso de algún generador reactivo previo a la falla. Otras fuentes de potencia reactiva que también se utilizarán incluyen condensadores en derivación, reactores en derivación, compensadores estáticos de VAR y circuitos de control de voltaje.
Sistemas polifásicos sinusoidales desequilibrados
Si bien la potencia activa y la potencia reactiva están bien definidas en cualquier sistema, la definición de potencia aparente para sistemas polifásicos desequilibrados se considera uno de los temas más controvertidos en la ingeniería eléctrica. Originalmente, la potencia aparente surgió simplemente como una figura de mérito. Las principales delineaciones del concepto se atribuyen a Fenómenos de retardo en la bobina de inducción de Stanley (1888) y Elementos teóricos de ingeniería de Steinmetz (1915). Sin embargo, con el desarrollo de la distribución de energía trifásica , quedó claro que la definición de potencia aparente y el factor de potencia no se podían aplicar a sistemas polifásicos desequilibrados . En 1920, un "Comité conjunto especial de la AIEE y la Asociación Nacional de Luz Eléctrica" se reunió para resolver el problema. Consideraron dos definiciones.
- ,
es decir, la suma aritmética de las potencias aparentes de fase; y
- ,
es decir, la magnitud de la potencia compleja trifásica total.
El comité de 1920 no llegó a ningún consenso y el tema siguió dominando las discusiones. En 1930, se formó otro comité y una vez más no logró resolver la cuestión. Las transcripciones de sus discusiones son las más largas y controvertidas jamás publicadas por la AIEE. [10] La resolución posterior de este debate no llegó hasta fines de la década de 1990.
En 1993, Alexander Emanuel propuso una nueva definición basada en la teoría de componentes simétricos para una carga lineal desequilibrada suministrada con voltajes sinusoidales asimétricos:
- ,
es decir, la raíz de las sumas al cuadrado de los voltajes de línea multiplicada por la raíz de las sumas al cuadrado de las corrientes de línea. denota la potencia de secuencia positiva:
denota el fasor de voltaje de secuencia positiva y denota el fasor de corriente de secuencia positiva. [10]
Fórmulas de números reales
Una resistencia perfecta no almacena energía, por lo que la corriente y el voltaje están en fase. Por lo tanto, no hay potencia reactiva y (usando la convención de signos pasivos ). Por lo tanto, para una resistencia perfecta
- .
En el caso de un capacitor o inductor perfecto, no hay transferencia de potencia neta, por lo que toda la potencia es reactiva. Por lo tanto, en el caso de un capacitor o inductor perfecto:
- .
¿Dónde está la reactancia del capacitor o inductor?
Si se define como positivo para un inductor y negativo para un capacitor, entonces los signos del módulo se pueden eliminar de S y X y obtener
- .
La potencia instantánea se define como:
- ,
donde y son las formas de onda de voltaje y corriente que varían en el tiempo.
Esta definición es útil porque se aplica a todas las formas de onda, ya sean sinusoidales o no. Esto resulta particularmente útil en electrónica de potencia, donde las formas de onda no sinusoidales son comunes.
En general, a los ingenieros les interesa la potencia activa promediada durante un período de tiempo, ya sea un ciclo de línea de baja frecuencia o un período de conmutación de convertidor de potencia de alta frecuencia. La forma más sencilla de obtener ese resultado es tomar la integral del cálculo instantáneo durante el período deseado:
- .
Este método de cálculo de la potencia media proporciona la potencia activa independientemente del contenido armónico de la forma de onda. En aplicaciones prácticas, esto se haría en el dominio digital, donde el cálculo se vuelve trivial en comparación con el uso de rms y fase para determinar la potencia activa:
- .
Sistemas de frecuencias múltiples
Dado que se puede calcular un valor RMS para cualquier forma de onda, se puede calcular la potencia aparente a partir de este. En el caso de la potencia activa, parecería a primera vista que sería necesario calcular muchos términos de producto y promediarlos todos. Sin embargo, si se analiza uno de estos términos de producto con más detalle, se obtiene un resultado muy interesante.
Sin embargo, el promedio temporal de una función de la forma cos( ωt + k ) es cero siempre que ω sea distinto de cero. Por lo tanto, los únicos términos del producto que tienen un promedio distinto de cero son aquellos en los que la frecuencia de la tensión y la corriente coinciden. En otras palabras, es posible calcular la potencia activa (promedio) simplemente tratando cada frecuencia por separado y sumando las respuestas. Además, si se supone que la tensión de la red eléctrica es una sola frecuencia (que suele ser el caso), esto demuestra que las corrientes armónicas son algo malo. Aumentarán la corriente RMS (ya que se añadirán términos distintos de cero) y, por tanto, la potencia aparente, pero no tendrán ningún efecto sobre la potencia activa transferida. Por tanto, las corrientes armónicas reducirán el factor de potencia. Las corrientes armónicas se pueden reducir mediante un filtro colocado en la entrada del dispositivo. Normalmente, este consistirá en un simple condensador (que se basa en la resistencia parásita y la inductancia de la fuente de alimentación) o en una red condensador-inductor. Un circuito de corrección del factor de potencia activo en la entrada generalmente reduciría aún más las corrientes armónicas y mantendría el factor de potencia más cerca de la unidad.
Véase también
Referencias
- ^ ab IEEE Definiciones estándar para la medición de magnitudes de potencia eléctrica en condiciones sinusoidales, no sinusoidales, equilibradas o desequilibradas . IEEE. 2010. doi :10.1109/IEEESTD.2010.5439063. ISBN 978-0-7381-6058-0.
- ^ Thomas, Roland E.; Rosa, Albert J.; Toussaint, Gregory J. (2016). El análisis y diseño de circuitos lineales (8.ª ed.). Wiley. págs. 812–813. ISBN 978-1-119-23538-5.
- ^ Das, JC (2015). Armónicos del sistema de potencia y diseño de filtros pasivos . Wiley, IEEE Press. pág. 2. ISBN 978-1-118-86162-2Para distinguir entre cargas lineales y no lineales
, podemos decir que las cargas lineales invariantes en el tiempo se caracterizan de modo que la aplicación de un voltaje sinusoidal da como resultado un flujo sinusoidal de corriente.
- ^ "Importancia de la potencia reactiva para el sistema". 21 de marzo de 2011. Archivado desde el original el 12 de mayo de 2015. Consultado el 29 de abril de 2015 .
- ^ Definición de potencia activa en el Vocabulario Electrotécnico Internacional Archivado el 23 de abril de 2015 en Wayback Machine .
- ^ IEEE 100: el diccionario autorizado de términos de estándares IEEE.-7.ª ed. ISBN 0-7381-2601-2 , página 23
- ^ "14 de agosto de 2003: corte de suministro eléctrico: secuencia de eventos" (PDF) . FERC . 12 de septiembre de 2003. Archivado desde el original (PDF) el 20 de octubre de 2007 . Consultado el 18 de febrero de 2008 .
- ^ Close, Charles M. El análisis de circuitos lineales . págs. 398 (sección 8.3).
- ^ "Diferenciación de carga". Archivado desde el original el 25 de octubre de 2015. Consultado el 29 de abril de 2015 .
- ^ ab Emanuel, Alexander (julio de 1993). "Sobre la definición de factor de potencia y potencia aparente en circuitos polifásicos desequilibrados con voltaje y corrientes sinusoidales". IEEE Transactions on Power Delivery . 8 (3): 841–852. doi :10.1109/61.252612.
Enlaces externos
- "Applet Java de alimentación de CA"

































![{\displaystyle P_{\text{promedio}}={\frac {1}{n}}\sum _{k=1}^{n}V[k]I[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea58eff331b5263dbf27b58073ba0a5f0a0e68bf)
![{\displaystyle {\begin{aligned}&A\cos(\omega _{1}t+k_{1})\cos(\omega _{2}t+k_{2})\\={}&{\frac {A}{2}}\cos \left[\left(\omega _{1}t+k_{1}\right)+\left(\omega _{2}t+k_{2}\right)\right]+{\frac {A}{2}}\cos \left[\left(\omega _{1}t+k_{1}\right)-\left(\omega _{2}t+k_{2}\right)\right]\\={}&{\frac {A}{2}}\cos \left[\left(\omega _{1}+\omega _{2}\right)t+k_{1}+k_{2}\right]+{\frac {A}{2}}\cos \left[\left(\omega _{1}-\omega _{2}\right)t+k_{1}-k_{2}\right]\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c773be852c41c009df2d70fc4d2e5d7ef7a36ac)
