Palanca

Palanca
Las palancas se pueden utilizar para ejercer una gran fuerza sobre una pequeña distancia en un extremo ejerciendo sólo una pequeña fuerza (esfuerzo) sobre una distancia mayor en el otro.
Clasificación	Máquina simple
Componentes	Punto de apoyo o pivote, carga y esfuerzo
Ejemplos	balancín, abridor de botellas, etc.

Una palanca es una máquina simple que consiste en una viga o varilla rígida que pivota en una bisagra fija o fulcro . Una palanca es un cuerpo rígido capaz de girar sobre un punto sobre sí mismo. Sobre la base de las ubicaciones del fulcro, la carga y el esfuerzo, la palanca se divide en tres tipos. Es una de las seis máquinas simples identificadas por los científicos del Renacimiento. Una palanca amplifica una fuerza de entrada para proporcionar una mayor fuerza de salida, que se dice que proporciona apalancamiento , que es una ventaja mecánica obtenida en el sistema, igual a la relación entre la fuerza de salida y la fuerza de entrada. Como tal, la palanca es un dispositivo de ventaja mecánica , que intercambia fuerza por movimiento.

La palabra "lever" entró en el inglés alrededor del año 1300 d. C. a partir del francés antiguo levier . Este surgió de la raíz del verbo " lever" , que significa "levantar". El verbo, a su vez, se remonta al latín levare , [ ^1] a su vez del adjetivo levis , que significa "ligero" (como en "no pesado"). El origen principal de la palabra es la raíz protoindoeuropea legwh- , que significa "ligero", "fácil" o "ágil", entre otras cosas. La raíz PIE también dio lugar a la palabra inglesa "light". ^[2]

La evidencia más temprana del mecanismo de palanca se remonta al antiguo Cercano Oriente alrededor del  5000 a. C. , cuando se utilizó por primera vez en una balanza simple . ^[3] En el antiguo Egipto alrededor  del 4400 a. C. , se utilizó un pedal para el telar de marco horizontal más antiguo . ^[4] En Mesopotamia (Irak moderno) alrededor  del 3000 a. C. , se inventó el shadouf , un dispositivo similar a una grúa que utiliza un mecanismo de palanca. ^[3] En el antiguo Egipto , los trabajadores usaban la palanca para mover y levantar obeliscos que pesaban más de 100 toneladas. Esto es evidente por los huecos en los grandes bloques y los salientes de manipulación que no podían usarse para ningún otro propósito que no fuera el de palancas. ^[5]

Los primeros escritos que quedan sobre palancas datan del siglo III a. C. y fueron proporcionados, según la creencia común, por el matemático griego Arquímedes , quien afirmó la famosa frase: "Dadme una palanca lo suficientemente larga y un punto de apoyo sobre el cual colocarla, y moveré el mundo".

Autumn Stanley sostiene que el palo para cavar puede considerarse la primera palanca, lo que posicionaría a las mujeres prehistóricas como las inventoras de la tecnología de palanca. ^[6]

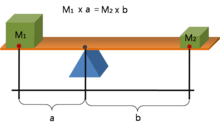
Una palanca es una viga conectada al suelo mediante una bisagra o pivote, llamado fulcro. La palanca ideal no disipa ni almacena energía, lo que significa que no hay fricción en la bisagra ni flexión en la viga. En este caso, la potencia que entra en la palanca es igual a la potencia que sale, y la relación entre la fuerza de salida y la fuerza de entrada está dada por la relación entre las distancias desde el fulcro hasta los puntos de aplicación de estas fuerzas. Esto se conoce como la ley de la palanca .

La ventaja mecánica de una palanca se puede determinar considerando el equilibrio de momentos o torque , T , en torno al punto de apoyo. Si la distancia recorrida es mayor, entonces la fuerza de salida es menor.

$${\displaystyle {\begin{aligned}T_{1}&=F_{1}a,\quad \\T_{2}&=F_{2}b\!\end{aligned}}}$$

donde F ₁ es la fuerza de entrada a la palanca y F ₂ es la fuerza de salida. Las distancias a y b son las distancias perpendiculares entre las fuerzas y el fulcro.

Como los momentos de torsión deben estar equilibrados, . Por lo tanto, .${\displaystyle T_{1}=T_{2}\!}$${\displaystyle F_{1}a=F_{2}b\!}$

La ventaja mecánica de una palanca es la relación entre la fuerza de salida y la fuerza de entrada.

$${\displaystyle MA={\frac {F_{2}}{F_{1}}}={\frac {a}{b}}.\!}$$

Esta relación muestra que la ventaja mecánica se puede calcular a partir de la relación de las distancias desde el punto de apoyo hasta el punto donde se aplican las fuerzas de entrada y salida a la palanca, suponiendo que la palanca no tiene peso y no hay pérdidas por fricción, flexibilidad o desgaste. Esto sigue siendo cierto aunque la distancia "horizontal" (perpendicular a la fuerza de gravedad) de a y b cambie (disminuya) a medida que la palanca cambia a cualquier posición que se aleje de la horizontal.

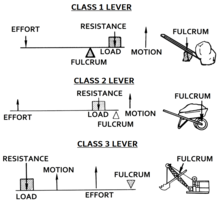
Las palancas se clasifican según la posición relativa del fulcro, el esfuerzo y la resistencia (o carga). Es habitual denominar a la fuerza de entrada «esfuerzo» y a la fuerza de salida «carga» o «resistencia». Esto permite identificar tres clases de palancas según la posición relativa del fulcro, la resistencia y el esfuerzo: ^[7]

• Clase I – El punto de apoyo se encuentra entre el esfuerzo y la resistencia: el esfuerzo se aplica en un lado del punto de apoyo y la resistencia (o carga) en el otro lado. Por ejemplo, un balancín , una palanca , unas tijeras , una balanza , un par de alicates y un martillo de uña (para sacar un clavo). Con el punto de apoyo en el medio, la ventaja mecánica de la palanca puede ser mayor, menor o incluso igual a 1.
• Clase II – La resistencia (o carga) se encuentra entre el esfuerzo y el fulcro: el esfuerzo se aplica en un lado de la resistencia y el fulcro se encuentra en el otro lado, p. ej., una carretilla, un cascanueces , un abridor de botellas , una llave inglesa y el pedal de freno de un automóvil. Como el brazo de carga es más pequeño que el brazo de esfuerzo, la ventaja mecánica de la palanca siempre es mayor que 1. También se denomina palanca multiplicadora de fuerza.
• Clase III – El esfuerzo se encuentra entre la resistencia y el fulcro: La resistencia (o carga) se aplica en un lado del esfuerzo y el fulcro se encuentra en el otro lado, p. ej., un par de pinzas , un martillo , un par de tenazas , una caña de pescar y la mandíbula de un cráneo humano. Como el brazo de esfuerzo es más pequeño que el brazo de carga, la ventaja mecánica de la palanca siempre es menor que 1. También se denomina palanca multiplicadora de velocidad.

Estos casos se describen mediante el mnemónico fre 123 , donde el fulcro f está entre r y e para la palanca de primera clase, la resistencia r está entre f y e para la palanca de segunda clase, y el esfuerzo e está entre f y r para la palanca de tercera clase.

Una palanca compuesta está formada por varias palancas que actúan en serie: la resistencia de una palanca en un sistema de palancas actúa como esfuerzo para la siguiente y, por lo tanto, la fuerza aplicada se transfiere de una palanca a la siguiente. Entre los ejemplos de palancas compuestas se incluyen las balanzas, los cortaúñas y las teclas del piano.

El martillo , el yunque y el estribo son pequeños huesos en el oído medio , conectados como palancas compuestas, que transfieren ondas sonoras desde el tímpano hasta la ventana oval de la cóclea .

La palanca es una barra móvil que gira sobre un punto de apoyo fijado a un punto fijo. La palanca funciona aplicando fuerzas a diferentes distancias del punto de apoyo o pivote.

A medida que la palanca gira alrededor del punto de apoyo, los puntos más alejados de este pivote se mueven más rápido que los puntos más cercanos al pivote. Por lo tanto, una fuerza aplicada a un punto más alejado del pivote debe ser menor que la fuerza ubicada en un punto más cercano, porque la potencia es el producto de la fuerza por la velocidad. ^[8]

Si a y b son distancias desde el fulcro a los puntos A y B y la fuerza F _A aplicada a A es la entrada y la fuerza F _B aplicada en B es la salida, la relación de las velocidades de los puntos A y B está dada por a/b , por lo que tenemos que la relación entre la fuerza de salida y la fuerza de entrada, o ventaja mecánica, está dada por:$${\displaystyle MA={\frac {F_{B}}{F_{A}}}={\frac {a}{b}}.}$$

Esta es la ley de la palanca , que fue demostrada por Arquímedes usando razonamiento geométrico. ^[9] Muestra que si la distancia a desde el fulcro hasta donde se aplica la fuerza de entrada (punto A ) es mayor que la distancia b desde el fulcro hasta donde se aplica la fuerza de salida (punto B ), entonces la palanca amplifica la fuerza de entrada. Por otro lado, si la distancia a desde el fulcro hasta la fuerza de entrada es menor que la distancia b desde el fulcro hasta la fuerza de salida, entonces la palanca reduce la fuerza de entrada.

El uso de la velocidad en el análisis estático de una palanca es una aplicación del principio del trabajo virtual .

Una palanca se modela como una barra rígida conectada a un marco en el suelo mediante una articulación articulada llamada fulcro. La palanca se opera aplicando una fuerza de entrada F _A en un punto A ubicado por el vector de coordenadas r _A en la barra. Luego, la palanca ejerce una fuerza de salida F _B en el punto B ubicado por r _B . La rotación de la palanca alrededor del fulcro P se define por el ángulo de rotación θ en radianes.

Sea r _P el vector de coordenadas del punto P que define el fulcro , e introduzcamos las longitudes

$${\displaystyle a=|\mathbf {r} _{A}-\mathbf {r} _{P}|,\quad b=|\mathbf {r} _{B}-\mathbf {r} _{P}|,}$$

que son las distancias desde el fulcro al punto de entrada A y al punto de salida B , respectivamente.

Ahora introduzca los vectores unitarios e _A y e _B desde el fulcro hasta el punto A y B , de modo que

$${\displaystyle \mathbf {r} _{A}-\mathbf {r} _{P}=a\mathbf {e} _{A},\quad \mathbf {r} _{B}-\mathbf {r } _{P}=b\mathbf {e} _{B}.}$$

La velocidad de los puntos A y B se obtiene como

$${\displaystyle \mathbf {v} _{A}={\dot {\theta }}a\mathbf {e} _{A}^{\perp },\quad \mathbf {v} _{B}={ \dot {\theta }}b\mathbf {e} _ {B}^{\perp },}$$

donde e _A ^⊥ y e _B ^⊥ son vectores unitarios perpendiculares a e _A y e _B , respectivamente.

El ángulo θ es la coordenada generalizada que define la configuración de la palanca, y la fuerza generalizada asociada a esta coordenada viene dada por

$${\displaystyle F_{\theta }=\mathbf {F} _{A}\cdot {\frac {\partial \mathbf {v} _{A}}{\partial {\dot {\theta }}}}- \mathbf {F} _{B}\cdot {\frac {\partial \mathbf {v} _{B}}{\partial {\dot {\theta }}}}=a(\mathbf {F} _{ A}\cdot \mathbf {e} _{A}^{\perp })-b(\mathbf {F} _{B}\cdot \mathbf {e} _{B}^{\perp })=aF_ {A}-bF_{B},}$$

donde F _A y F _B son componentes de las fuerzas que son perpendiculares a los segmentos radiales PA y PB . El principio del trabajo virtual establece que en equilibrio la fuerza generalizada es cero, es decir

$${\displaystyle F_{\theta}=aF_{A}-bF_{B}=0.\,\!}$$

Por lo tanto, la relación entre la fuerza de salida F _B y la fuerza de entrada F _A se obtiene como

$${\displaystyle MA={\frac {F_{B}}{F_{A}}}={\frac {a}{b}},}$$

¿Cuál es la ventaja mecánica de la palanca?

Esta ecuación muestra que si la distancia a desde el fulcro hasta el punto A donde se aplica la fuerza de entrada es mayor que la distancia b desde el fulcro hasta el punto B donde se aplica la fuerza de salida, entonces la palanca amplifica la fuerza de entrada. Si ocurre lo contrario, es decir, que la distancia desde el fulcro hasta el punto de entrada A es menor que la distancia desde el fulcro hasta el punto de salida B , entonces la palanca reduce la magnitud de la fuerza de entrada.

Wikimedia Commons alberga una categoría multimedia sobre Palancas .

Busque palanca en Wikcionario, el diccionario libre.

• Palanca en la enciclopedia de ciencia e ingeniería de Diracdelta
• Una palanca simple por Stephen Wolfram , Proyecto de demostraciones Wolfram .
• Palancas: máquinas simples en EnchantedLearning.com