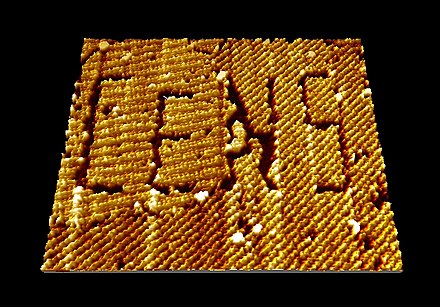Microscopio de efecto túnel de barrido

Un microscopio de efecto túnel de barrido ( STM ) es un tipo de microscopio de sonda de barrido utilizado para obtener imágenes de superficies a nivel atómico . Su desarrollo en 1981 le valió a sus inventores, Gerd Binnig y Heinrich Rohrer , entonces en IBM Zürich , el Premio Nobel de Física en 1986. ^{[1] [2] [3]} El STM detecta la superficie mediante una punta conductora extremadamente afilada que puede distinguir características menores a 0,1  nm con una resolución de profundidad de 0,01 nm (10  pm ). ^[4] Esto significa que se pueden obtener imágenes y manipular átomos individuales de forma rutinaria. La mayoría de los microscopios de efecto túnel de barrido están diseñados para su uso en ultra alto vacío a temperaturas cercanas al cero absoluto , pero existen variantes para estudios en aire, agua y otros entornos, y para temperaturas superiores a 1000 °C. ^{[5] [6]}

El STM se basa en el concepto de efecto túnel cuántico . Cuando la punta se acerca mucho a la superficie que se va a examinar, se aplica un voltaje de polarización entre ambos para que los electrones hagan un túnel a través del vacío que los separa. La corriente de efecto túnel resultante es una función de la posición de la punta, el voltaje aplicado y la densidad local de estados (LDOS) de la muestra. La información se adquiere controlando la corriente a medida que la punta recorre la superficie y, por lo general, se muestra en forma de imagen. ^[5]

Una mejora de la técnica conocida como espectroscopia de efecto túnel consiste en mantener la punta en una posición constante sobre la superficie, variando el voltaje de polarización y registrando el cambio resultante en la corriente. Mediante esta técnica, se puede reconstruir la densidad local de los estados electrónicos. ^[7] Esto se realiza a veces en campos magnéticos elevados y en presencia de impurezas para inferir las propiedades e interacciones de los electrones en el material estudiado.

La microscopía de efecto túnel puede ser una técnica desafiante, ya que requiere superficies extremadamente limpias y estables, puntas afiladas, excelente aislamiento de vibraciones y electrónica sofisticada. No obstante, muchos aficionados construyen sus propios microscopios. ^[8]

La punta se acerca a la muestra mediante un mecanismo de posicionamiento grueso que generalmente se monitorea visualmente. A corta distancia, se logra un control fino de la posición de la punta con respecto a la superficie de la muestra mediante tubos de escáner piezoeléctricos cuya longitud se puede alterar mediante un voltaje de control. Se aplica un voltaje de polarización entre la muestra y la punta, y el escáner se alarga gradualmente hasta que la punta comienza a recibir la corriente de tunelización. La separación punta-muestra w se mantiene entonces en algún lugar en el rango de 4-7  Å (0,4-0,7  nm ), ligeramente por encima de la altura donde la punta experimentaría una interacción repulsiva ( w < 3 Å), pero aún en la región donde existe una interacción atractiva (3 < w < 10 Å). ^[5] La corriente de tunelización, que está en el rango de sub- nanoamperios , se amplifica lo más cerca posible del escáner. Una vez que se establece la tunelización, el sesgo de la muestra y la posición de la punta con respecto a la muestra se varían de acuerdo con los requisitos del experimento.

A medida que la punta se mueve a lo largo de la superficie en una matriz x – y discreta , los cambios en la altura de la superficie y la población de los estados electrónicos provocan cambios en la corriente de tunelización. Las imágenes digitales de la superficie se forman de una de dos maneras: en el modo de altura constante, los cambios de la corriente de tunelización se mapean directamente, mientras que en el modo de corriente constante, el voltaje que controla la altura ( z ) de la punta se registra mientras la corriente de tunelización se mantiene a un nivel predeterminado. ^[5]

En el modo de corriente constante, la electrónica de retroalimentación ajusta la altura mediante un voltaje aplicado al mecanismo piezoeléctrico de control de altura. Si en algún momento la corriente de tunelización está por debajo del nivel establecido, la punta se mueve hacia la muestra y viceversa. Este modo es relativamente lento, ya que la electrónica necesita verificar la corriente de tunelización y ajustar la altura en un bucle de retroalimentación en cada punto medido de la superficie. Cuando la superficie es atómicamente plana, el voltaje aplicado al escáner z refleja principalmente variaciones en la densidad de carga local. Pero cuando se encuentra un escalón atómico, o cuando la superficie se comba debido a la reconstrucción , la altura del escáner también debe cambiar debido a la topografía general. La imagen formada de los voltajes del escáner z que se necesitaron para mantener constante la corriente de tunelización mientras la punta escaneaba la superficie contiene datos topográficos y de densidad electrónica. En algunos casos, puede que no esté claro si los cambios de altura se produjeron como resultado de uno u otro.

En el modo de altura constante, el voltaje del escáner z se mantiene constante a medida que el escáner oscila de un lado a otro sobre la superficie y se representa la corriente de tunelización, que depende exponencialmente de la distancia. Este modo de operación es más rápido, pero en superficies rugosas, donde puede haber grandes moléculas adsorbidas, o crestas y surcos, la punta corre el riesgo de chocar.

El escaneo rasterizado de la punta es una matriz de 128×128 a 1024×1024 (o más), y para cada punto del raster se obtiene un único valor. Por lo tanto, las imágenes producidas por STM son en escala de grises y el color solo se agrega en el posprocesamiento para enfatizar visualmente las características importantes.

Además de escanear la muestra, se puede obtener información sobre la estructura electrónica en una ubicación determinada de la misma barriendo el voltaje de polarización (junto con una pequeña modulación de CA para medir directamente la derivada) y midiendo el cambio de corriente en una ubicación específica. ^[4] Este tipo de medición se denomina espectroscopia de efecto túnel de barrido (STS) y normalmente da como resultado un gráfico de la densidad local de estados en función de la energía de los electrones dentro de la muestra. La ventaja de la STM sobre otras mediciones de la densidad de estados radica en su capacidad para realizar mediciones extremadamente locales. Así es como, por ejemplo, la densidad de estados en un sitio de impureza se puede comparar con la densidad de estados alrededor de la impureza y en otras partes de la superficie. ^[9]

Los componentes principales de un microscopio de efecto túnel son la punta de escaneo, el escáner de altura ( eje z ) y lateral ( ejes x e y ) controlados piezoeléctricamente y el mecanismo de aproximación de la muestra gruesa a la punta. El microscopio está controlado por una electrónica dedicada y una computadora. El sistema está soportado por un sistema de aislamiento de vibraciones. ^[5]

La punta suele estar hecha de tungsteno o alambre de platino-iridio , aunque también se utiliza oro . ^[4] Las puntas de tungsteno suelen fabricarse mediante grabado electroquímico, y las de platino-iridio mediante corte mecánico. La resolución de una imagen está limitada por el radio de curvatura de la punta de escaneo. A veces, se producen artefactos de imagen si la punta tiene más de un vértice en el extremo; lo más frecuente es observar imágenes de doble punta , una situación en la que dos vértices contribuyen por igual al efecto túnel. ^[4] Si bien se conocen varios procesos para obtener puntas afiladas y utilizables, la prueba definitiva de calidad de la punta solo es posible cuando se realiza el efecto túnel en el vacío. De vez en cuando, las puntas se pueden acondicionar aplicando altos voltajes cuando ya están en el rango de efecto túnel, o haciendo que recojan un átomo o una molécula de la superficie.

En la mayoría de los diseños modernos, el escáner es un tubo hueco de un piezoeléctrico polarizado radialmente con superficies metalizadas. La superficie exterior está dividida en cuatro cuadrantes largos para servir como electrodos de movimiento x e y con voltajes de deflexión de dos polaridades aplicadas en los lados opuestos. El material del tubo es una cerámica de titanato de zirconato de plomo con una constante piezoeléctrica de aproximadamente 5 nanómetros por voltio. La punta está montada en el centro del tubo. Debido a cierta diafonía entre los electrodos y las no linealidades inherentes, el movimiento se calibra y los voltajes necesarios para el movimiento independiente x , y y z se aplican de acuerdo con las tablas de calibración. ^[5]

Debido a la extrema sensibilidad de la corriente de efecto túnel a la separación de los electrodos, es imprescindible un aislamiento de vibraciones adecuado o un cuerpo rígido del microscopio de barrido para obtener resultados utilizables. En el primer microscopio de barrido de Binnig y Rohrer, se utilizó levitación magnética para mantener el microscopio libre de vibraciones; ahora se emplean a menudo sistemas de resortes mecánicos o de resortes de gas . ^[5] Además, a veces se implementan mecanismos para amortiguar las vibraciones mediante corrientes de Foucault . Los microscopios diseñados para barridos largos en la espectroscopia de efecto túnel necesitan una estabilidad extrema y se construyen en cámaras anecoicas : salas de hormigón dedicadas con aislamiento acústico y electromagnético que, a su vez, flotan sobre dispositivos de aislamiento de vibraciones dentro del laboratorio.

El mantenimiento de la posición de la punta con respecto a la muestra, el escaneo de la muestra y la adquisición de los datos se controlan mediante computadora. Se utiliza un software específico para microscopías de sonda de escaneo para el procesamiento de imágenes, así como para la realización de mediciones cuantitativas. ^[10]

Algunos microscopios de efecto túnel son capaces de registrar imágenes a altas frecuencias de cuadro. ^{[11] [12]} Los videos hechos a partir de dichas imágenes pueden mostrar difusión superficial ^[13] o rastrear la adsorción y las reacciones en la superficie. En los microscopios de velocidad de video, se han logrado frecuencias de cuadro de 80 Hz con retroalimentación completamente funcional que ajusta la altura de la punta. ^[14]

El efecto túnel cuántico de los electrones es un concepto funcional de la mecánica cuántica que surge de la mecánica cuántica . Clásicamente, una partícula que choca contra una barrera impenetrable no la atravesará. Si la barrera se describe mediante un potencial que actúa a lo largo de la dirección z , en la que un electrón de masa m _e adquiere la energía potencial U ( z ), la trayectoria del electrón será determinista y tal que la suma E de sus energías cinética y potencial se conserva en todo momento:

${\displaystyle E={\frac {p^{2}}{2m_{\text{e}}}}+U(z).}$

El electrón tendrá un momento definido, distinto de cero , p solo en regiones donde la energía inicial E es mayor que U ( z ). Sin embargo, en física cuántica, el electrón puede pasar a través de regiones prohibidas clásicamente. Esto se conoce como efecto túnel . ^[5]

El modelo más simple de efecto túnel entre la muestra y la punta de un microscopio de efecto túnel de barrido es el de una barrera de potencial rectangular . ^{[15] [5]} Un electrón de energía E incide sobre una barrera de energía de altura U , en la región del espacio de ancho w . El comportamiento de un electrón en presencia de un potencial U ( z ), suponiendo un caso unidimensional, se describe mediante funciones de onda que satisfacen la ecuación de Schrödinger${\displaystyle \psi(z)}$

${\displaystyle -{\frac {\hbar ^{2}}{2m_{\text{e}}}}{\frac {\partial ^{2}\psi (z)}{\partial z^{2} }}+U(z)\,\psi (z)=E\,\psi (z),}$

donde ħ es la constante de Planck reducida , z es la posición y m _e es la masa del electrón . En las regiones de potencial cero en los dos lados de la barrera, la función de onda adopta las formas

${\displaystyle \psi _{L}(z)=e^{ikz}+r\,e^{-ikz}}$para z < 0,

${\displaystyle \psi _{R}(z)=t\,e^{ikz}}$para z > w ,

donde . Dentro de la barrera, donde E < U , la función de onda es una superposición de dos términos, cada uno de los cuales decae desde un lado de la barrera:${\displaystyle k={\tfrac {1}{\hbar }}{\sqrt {2m_{\text{e}}E}}}$

${\displaystyle \psi _{B}(z)=\xi e^{-\kappa z}+\zeta e^{\kappa z}}$para 0 < z < w ,

dónde .${\displaystyle \kappa ={\tfrac {1}{\hbar }}{\sqrt {2m_{\text{e}}(UE)}}}$

Los coeficientes r y t miden qué parte de la onda del electrón incidente se refleja o se transmite a través de la barrera. Es decir, de toda la corriente de partículas que choca, solo se transmite, como se puede ver en la expresión de corriente de probabilidad .${\displaystyle j_{i}=\hbar k/m_{\text{e}}}$${\displaystyle j_{t}=|t|^{2}\,j_{i}}$

${\displaystyle j_{t}=-i{\frac {\hbar }{2m_{\text{e}}}}\left\{\psi _{R}^{*}{\frac {\parcial }{\parcial z}}\psi _{R}-\psi _{R}{\frac {\parcial }{\parcial z}}\psi _{R}^{*}\right\},}$

que evalúa como . El coeficiente de transmisión se obtiene a partir de la condición de continuidad en las tres partes de la función de onda y sus derivadas en z = 0 y z = w (la derivación detallada se encuentra en el artículo Barrera de potencial rectangular ). Esto da donde . La expresión se puede simplificar aún más, de la siguiente manera:${\displaystyle j_{t}={\tfrac {\hbar k}{m_{\text{e}}}}\vert t\vert ^{2}}$${\displaystyle |t|^{2}={\big [}1+{\tfrac {1}{4}}\varepsilon ^{-1}(1-\varepsilon )^{-1}\sinh ^{2}\kappa w{\big ]}^{-1},}$${\displaystyle \varepsilon =E/U}$

En los experimentos STM, la altura típica de la barrera es del orden de la función de trabajo de superficie del material W , que para la mayoría de los metales tiene un valor entre 4 y 6 eV. ^[15] La función de trabajo es la energía mínima necesaria para llevar un electrón desde un nivel ocupado, el más alto de los cuales es el nivel de Fermi (para metales a T = 0 K), al nivel de vacío . Los electrones pueden hacer un túnel entre dos metales solo desde estados ocupados en un lado hacia los estados desocupados del otro lado de la barrera. Sin polarización, las energías de Fermi están al mismo nivel y no hay tunelización. La polarización desplaza las energías de los electrones en uno de los electrodos hacia arriba, y aquellos electrones que no tienen coincidencia en la misma energía en el otro lado harán un túnel. En los experimentos, se utilizan voltajes de polarización de una fracción de 1 V, por lo que es del orden de 10 a 12 nm ⁻¹ , mientras que w es unas décimas de nanómetro. La barrera es fuertemente atenuante. La expresión para la probabilidad de transmisión se reduce a La corriente de tunelización de un solo nivel es, por lo tanto, ^[15]${\estilo de visualización \kappa}$${\displaystyle |t|^{2}=16\,\varepsilon (1-\varepsilon )\,e^{-2\kappa w}.}$

${\displaystyle j_{t}=\left[{\frac {4k\kappa }{k^{2}+\kappa ^{2}}}\right]^{2}\,{\frac {\hbar k}{m_{\text{e}}}}\,e^{-2\kappa w},}$

donde ambos vectores de onda dependen de la energía del nivel E , y${\displaystyle k={\tfrac {1}{\hbar }}{\sqrt {2m_{\text{e}}E}},}$${\displaystyle \kappa ={\tfrac {1}{\hbar }}{\sqrt {2m_{\text{e}}(UE)}}.}$

La corriente de tunelización depende exponencialmente de la separación entre la muestra y la punta, y normalmente se reduce en un orden de magnitud cuando la separación aumenta en 1 Å (0,1 nm). ^[5] Debido a esto, incluso cuando la tunelización se produce desde una punta no idealmente afilada, la contribución dominante a la corriente proviene de su átomo u orbital más saliente. ^[15]

Como resultado de la restricción de que la tunelización desde un nivel de energía ocupado en un lado de la barrera requiere un nivel vacío de la misma energía en el otro lado de la barrera, la tunelización ocurre principalmente con electrones cerca del nivel de Fermi. La corriente de tunelización puede estar relacionada con la densidad de estados disponibles o llenos en la muestra. La corriente debida a un voltaje aplicado V (suponiendo que la tunelización ocurre desde la muestra hasta la punta) depende de dos factores: 1) el número de electrones entre el nivel de Fermi E _F y E _F  −  eV en la muestra, y 2) el número entre ellos que tienen estados libres correspondientes a los que tunelizar en el otro lado de la barrera en la punta. ^[5] Cuanto mayor sea la densidad de estados disponibles en la región de tunelización, mayor será la corriente de tunelización. Por convención, una V positiva significa que los electrones en la punta tunelizan hacia estados vacíos en la muestra; para un sesgo negativo, los electrones tunelizan desde los estados ocupados en la muestra hacia la punta. ^[5]

Para sesgos pequeños y temperaturas cercanas al cero absoluto, la cantidad de electrones en un volumen dado (la concentración de electrones) que están disponibles para el efecto túnel es el producto de la densidad de los estados electrónicos ρ ( E _F ) y el intervalo de energía entre los dos niveles de Fermi, eV . ^[5] La mitad de estos electrones se alejarán de la barrera. La otra mitad representará la corriente eléctrica que incide sobre la barrera, que está dada por el producto de la concentración de electrones, la carga y la velocidad v ( I _i  =  nev ), ^[5]

${\displaystyle I_{i}={\tfrac {1}{2}}e^{2}v\,\rho (E_{\text{F}})\,V.}$

La corriente eléctrica de tunelización será una pequeña fracción de la corriente incidente. La proporción está determinada por la probabilidad de transmisión T , ^[5] por lo que\

${\displaystyle I_{t}={\tfrac {1}{2}}e^{2}v\,\rho (E_{\text{F}})\,V\,T.}$

En el modelo más simple de una barrera de potencial rectangular, el coeficiente de probabilidad de transmisión T es igual a | t | ² .

Un modelo basado en funciones de onda más realistas para los dos electrodos fue ideado por John Bardeen en un estudio de la unión metal-aislante-metal . ^[16] Su modelo toma dos conjuntos ortonormales separados de funciones de onda para los dos electrodos y examina su evolución temporal a medida que los sistemas se acercan. ^{[5] [15]} El novedoso método de Bardeen, ingenioso en sí mismo, ^[5] resuelve un problema perturbativo dependiente del tiempo en el que la perturbación emerge de la interacción de los dos subsistemas en lugar de un potencial externo de la teoría de perturbación estándar de Rayleigh-Schrödinger .

Cada una de las funciones de onda para los electrones de la muestra (S) y la punta (T) se desintegra en el vacío después de chocar con la barrera de potencial de superficie, aproximadamente del tamaño de la función de trabajo de superficie. Las funciones de onda son las soluciones de dos ecuaciones de Schrödinger separadas para electrones en potenciales U _S y U _T . Cuando se factoriza la dependencia temporal de los estados de energías conocidas y , las funciones de onda tienen la siguiente forma general${\displaystyle E_{\mu }^{\text{S}}}$${\displaystyle E_{\nu }^{\text{T}}}$

${\displaystyle \psi _{\mu }^{\text{S}}(t)=\psi _{\mu }^{\text{S}}\exp \left(-{\frac {i}{\hbar }}E_{\mu }^{\text{S}}t\right),}$

${\displaystyle \psi _{\nu }^{\text{T}}(t)=\psi _{\nu }^{\text{T}}\exp \left(-{\frac {i}{\hbar }}E_{\nu }^{\text{T}}t\right).}$

Si los dos sistemas se acercan, pero siguen estando separados por una delgada región de vacío, el potencial que actúa sobre un electrón en el sistema combinado es U _T + U _S . Aquí, cada uno de los potenciales está limitado espacialmente a su propio lado de la barrera. Solo porque la cola de una función de onda de un electrodo está en el rango del potencial del otro, existe una probabilidad finita de que cualquier estado evolucione con el tiempo hacia los estados del otro electrodo. ^[5] El futuro del estado de la muestra μ se puede escribir como una combinación lineal con coeficientes dependientes del tiempo de y todos :${\displaystyle \psi _{\mu }^{\text{S}}(t)}$${\displaystyle \psi _{\nu }^{\text{T}}(t)}$

${\displaystyle \psi (t)=\psi _{\mu }^{\text{S}}(t)+\sum _{\nu }c_{\nu }(t)\psi _{\nu }^{\text{T}}(t)}$

con la condición inicial . ^[5] Cuando la nueva función de onda se inserta en la ecuación de Schrödinger para el potencial U _T + U _S , la ecuación obtenida se proyecta sobre cada una por separado (es decir, la ecuación se multiplica por a y se integra sobre todo el volumen) para distinguir los coeficientes Todos se toman como casi ortogonales a todos (su superposición es una pequeña fracción de las funciones de onda totales), y solo se conservan las cantidades de primer orden. En consecuencia, la evolución temporal de los coeficientes está dada por${\displaystyle c_{\nu}(0)=0}$${\displaystyle \psi _{\nu }^{\text{T}}}$${\displaystyle {\psi _{\nu }^{\text{T}}}^{*}}$${\displaystyle c_{\nu}.}$${\displaystyle \psi _{\mu }^{\text{S}}}$${\displaystyle \psi _{\nu }^{\text{T}}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}c_{\nu }(t)=-{\frac {i}{\hbar }}\int \psi _{\mu }^{\text{S}}\,U_{\text{T}}\,{\psi _{\nu }^{\text{T}}}^{*}\,\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z\,\exp \left[-{\frac {i}{\hbar }}(E_{\mu }^{\text{S}}-E_{\nu }^{\text{T}})t\right].}$

Como el potencial U _T es cero a una distancia de unos pocos diámetros atómicos de la superficie del electrodo, la integración sobre z se puede realizar desde un punto z ₀ en algún lugar dentro de la barrera y dentro del volumen de la punta ( z  >  z ₀ ).

Si el elemento de la matriz de tunelización se define como

${\displaystyle M_{\mu \nu }=\int _{z>z_{0}}\psi _{\mu }^{\text{S}}\,U_{\text{T}}\,{\psi _{\nu }^{\text{T}}}^{*}\,\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z,}$

la probabilidad de que el estado de la muestra μ evolucione en el tiempo t al estado de la punta ν es

${\displaystyle |c_{\nu }(t)|^{2}=|M_{\mu \nu }|^{2}{\frac {4\sin ^{2}{\big [}{\tfrac {1}{2\hbar }}(E_{\mu }^{\text{S}}-E_{\nu }^{\text{T}})t{\big ]}}{(E_{\mu }^{\text{S}}-E_{\nu }^{\text{T}})^{2}}}.}$

En un sistema con muchos electrones que inciden sobre la barrera, esta probabilidad dará la proporción de aquellos que logran el efecto túnel. Si en un momento t esta fracción era, en un momento posterior t  + d t la fracción total de electrones que habrían realizado el efecto túnel. La corriente de electrones que realizan el efecto túnel en cada caso es, por lo tanto, proporcional a dividido por que es la derivada temporal de ^[15]${\displaystyle |c_{\nu }(t)|^{2},}$${\displaystyle |c_{\nu }(t+\mathrm {d} t)|^{2}}$${\displaystyle |c_{\nu }(t+\mathrm {d} t)|^{2}-|c_{\nu }(t)|^{2}}$${\displaystyle \mathrm {d} t,}$${\displaystyle |c_{\nu }(t)|^{2},}$

${\displaystyle \Gamma _{\mu \to \nu }\ {\overset {\text{def}}{=}}\ {\frac {\mathrm {d} }{\mathrm {d} t}}|c_{\nu }(t)|^{2}={\frac {2\pi }{\hbar }}|M_{\mu \nu }|^{2}{\frac {\sin {\big [}(E_{\mu }^{\text{S}}-E_{\nu }^{\text{T}}){\tfrac {t}{\hbar }}{\big ]}}{\pi (E_{\mu }^{\text{S}}-E_{\nu }^{\text{T}})}}.}$

La escala de tiempo de la medición en STM es muchos órdenes de magnitud mayor que la escala de tiempo típica de femtosegundos de los procesos electrónicos en materiales, y es grande. La parte fraccionaria de la fórmula es una función de oscilación rápida de que decae rápidamente alejándose del pico central, donde . En otras palabras, el proceso de tunelización más probable, con diferencia, es el elástico, en el que se conserva la energía del electrón. La fracción, como se escribió anteriormente, es una representación de la función delta , por lo que${\displaystyle t/\hbar }$${\displaystyle (E_{\mu }^{\text{S}}-E_{\nu }^{\text{T}})}$${\displaystyle E_{\mu }^{\text{S}}=E_{\nu }^{\text{T}}}$

${\displaystyle \Gamma _{\mu \to \nu }={\frac {2\pi }{\hbar }}|M_{\mu \nu }|^{2}\delta (E_{\mu }^{\text{S}}-E_{\nu }^{\text{T}}).}$

Los sistemas de estado sólido se describen comúnmente en términos de niveles de energía continuos en lugar de discretos. El término puede considerarse como la densidad de estados de la punta en la energía que da${\displaystyle \delta (E_{\mu }^{\text{S}}-E_{\nu }^{\text{T}})}$${\displaystyle E_{\mu }^{\text{S}},}$

${\displaystyle \Gamma _{\mu \to \nu }={\frac {2\pi }{\hbar }}|M_{\mu \nu }|^{2}\rho _{\text{T}}(E_{\mu }^{\text{S}}).}$

El número de niveles de energía en la muestra entre las energías y es Cuando están ocupados, estos niveles son degenerados por espín (excepto en unas pocas clases especiales de materiales) y contienen carga de cualquiera de los espines. Con la muestra sesgada a voltaje, el efecto túnel puede ocurrir solo entre estados cuyas ocupaciones, dadas para cada electrodo por la distribución de Fermi-Dirac , no son las mismas, es decir, cuando uno u otro está ocupado, pero no ambos. Esto será para todas las energías para las que no es cero. Por ejemplo, un electrón hará un efecto túnel desde el nivel de energía en la muestra al nivel de energía en la punta ( ), un electrón en en la muestra encontrará estados desocupados en la punta en ( ), y lo mismo será para todas las energías intermedias. La corriente de efecto túnel es, por lo tanto, la suma de pequeñas contribuciones sobre todas estas energías del producto de tres factores: que representan los electrones disponibles, para aquellos a los que se les permite hacer un efecto túnel, y el factor de probabilidad para aquellos que realmente harán un efecto túnel:${\displaystyle \varepsilon }$${\displaystyle \varepsilon +\mathrm {d} \varepsilon }$${\displaystyle \rho _{\text{S}}(\varepsilon )\,\mathrm {d} \varepsilon .}$${\displaystyle 2e\cdot \rho _{\text{S}}(\varepsilon )\,\mathrm {d} \varepsilon }$${\displaystyle V,}$ ${\displaystyle f}$${\displaystyle \varepsilon }$${\displaystyle f(E_{\text{F}}-eV+\varepsilon )-f(E_{\text{F}}+\varepsilon )}$${\displaystyle E_{\text{F}}-eV}$${\displaystyle E_{\text{F}}}$${\displaystyle \varepsilon =0}$${\displaystyle E_{\text{F}}}$${\displaystyle E_{\text{F}}+eV}$${\displaystyle \varepsilon =eV}$${\displaystyle 2e\cdot \rho _{\text{S}}(E_{\text{F}}-eV+\varepsilon )\,\mathrm {d} \varepsilon }$${\displaystyle f(E_{\text{F}}-eV+\varepsilon )-f(E_{\text{F}}+\varepsilon )}$${\displaystyle \Gamma }$

${\displaystyle I_{t}={\frac {4\pi e}{\hbar }}\int _{-\infty }^{+\infty }[f(E_{\text{F}}-eV+\varepsilon )-f(E_{\text{F}}+\varepsilon )]\,\rho _{\text{S}}(E_{\text{F}}-eV+\varepsilon )\,\rho _{\text{T}}(E_{\text{F}}+\varepsilon )\,|M|^{2}\,d\varepsilon .}$

Los experimentos típicos se realizan a una temperatura de helio líquido (alrededor de 4 K), en la que el límite de corte del nivel de Fermi de la población de electrones es de menos de un milielectronvoltio de ancho. Las energías permitidas son solo aquellas entre los dos niveles de Fermi escalonados, y la integral se convierte en

${\displaystyle I_{t}={\frac {4\pi e}{\hbar }}\int _{0}^{eV}\rho _{\text{S}}(E_{\text{F}}-eV+\varepsilon )\,\rho _{\text{T}}(E_{\text{F}}+\varepsilon )\,|M|^{2}\,d\varepsilon .}$

Cuando el sesgo es pequeño, es razonable suponer que las funciones de onda de los electrones y, en consecuencia, el elemento de la matriz de tunelización no cambian significativamente en el estrecho rango de energías. Entonces, la corriente de tunelización es simplemente la convolución de las densidades de estados de la superficie de la muestra y la punta:

${\displaystyle I_{t}\propto \int _{0}^{eV}\rho _{\text{S}}(E_{\text{F}}-eV+\varepsilon )\,\rho _{\text{T}}(E_{\text{F}}+\varepsilon )\,d\varepsilon .}$

La forma en que la corriente de tunelización depende de la distancia entre los dos electrodos está contenida en el elemento de matriz de tunelización

${\displaystyle M_{\mu \nu }=\int _{z>z_{0}}\psi _{\mu }^{\text{S}}\,U_{\text{T}}\,{\psi _{\nu }^{\text{T}}}^{*}\,\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z.}$

Esta fórmula se puede transformar de modo que no quede ninguna dependencia explícita del potencial. Primero, se saca la parte de la ecuación de Schrödinger para la punta y se utiliza la condición de efecto túnel elástico de modo que${\displaystyle U_{\text{T}}\,{\psi _{\nu }^{\text{T}}}^{*}}$

${\displaystyle M_{\mu \nu }=\int _{z>z_{0}}\left({\psi _{\nu }^{\text{T}}}^{*}E_{\mu }\psi _{\mu }^{\text{S}}+\psi _{\mu }^{\text{S}}{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}}{\partial z^{2}}}{\psi _{\nu }^{\text{T}}}^{*}\right)\,\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z.}$

Ahora está presente en la ecuación de Schrödinger para la muestra y es igual al operador cinético más el operador potencial que actúa sobre Sin embargo, la parte potencial que contiene U _S está en el lado de la punta de la barrera casi cero. Lo que queda,${\displaystyle E_{\mu }\,{\psi _{\mu }^{\text{S}}}}$${\displaystyle \psi _{\mu }^{\text{S}}.}$

${\displaystyle M_{\mu \nu }=-{\frac {\hbar ^{2}}{2m}}\int _{z>z_{0}}\left({\psi _{\nu }^{\text{T}}}^{*}{\frac {\partial ^{2}}{\partial z^{2}}}{\psi _{\mu }^{\text{S}}}-{\psi _{\mu }^{\text{S}}}{\frac {\partial ^{2}}{\partial z^{2}}}{\psi _{\nu }^{\text{T}}}^{*}\right)\,\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z,}$

se puede integrar sobre z porque el integrando entre paréntesis es igual a${\displaystyle \partial _{z}\left({\psi _{\nu }^{\text{T}}}^{*}\,\partial _{z}\psi _{\mu }^{\text{S}}-{\psi _{\mu }^{\text{S}}}\,\partial _{z}{\psi _{\nu }^{\text{T}}}^{*}\right).}$

El elemento de matriz de tunelización de Bardeen es una integral de las funciones de onda y sus gradientes sobre una superficie que separa los dos electrodos planos:

${\displaystyle M_{\mu \nu }={\frac {\hbar ^{2}}{2m}}\int _{z=z_{0}}\left({\psi _{\mu }^{\text{S}}}{\frac {\partial }{\partial z}}{\psi _{\nu }^{\text{T}}}^{*}-{\psi _{\nu }^{\text{T}}}^{*}{\frac {\partial }{\partial z}}{\psi _{\mu }^{\text{S}}}\right)\,\mathrm {d} x\,\mathrm {d} y.}$

La dependencia exponencial de la corriente de tunelización con respecto a la separación de los electrodos proviene de las mismas funciones de onda que se filtran a través del paso de potencial en la superficie y exhiben un decaimiento exponencial hacia la región clásicamente prohibida fuera del material.

Los elementos de la matriz de tunelización muestran una dependencia apreciable de la energía, que es tal que la tunelización desde el extremo superior del intervalo eV es casi un orden de magnitud más probable que la tunelización desde los estados en su parte inferior. Cuando la muestra está sesgada positivamente, sus niveles desocupados se sondean como si la densidad de estados de la punta estuviera concentrada en su nivel de Fermi. Por el contrario, cuando la muestra está sesgada negativamente, sus estados electrónicos ocupados se sondean, pero el espectro de los estados electrónicos de la punta domina. En este caso es importante que la densidad de estados de la punta sea lo más plana posible. ^[5]

Se pueden obtener resultados idénticos a los de Bardeen considerando el enfoque adiabático de los dos electrodos y utilizando la teoría de perturbación dependiente del tiempo estándar. ^[15] Esto conduce a la regla de oro de Fermi para la probabilidad de transición en la forma dada anteriormente.${\displaystyle \Gamma _{\mu \to \nu }}$

El modelo de Bardeen es para el efecto túnel entre dos electrodos planos y no explica la resolución lateral del microscopio de efecto túnel de barrido. Tersoff y Hamann ^{[17] [18] [19]} utilizaron la teoría de Bardeen y modelaron la punta como un punto geométrico sin estructura. ^[5] Esto les ayudó a desenredar las propiedades de la punta (que son difíciles de modelar) de las propiedades de la superficie de la muestra. El resultado principal fue que la corriente de efecto túnel es proporcional a la densidad local de estados de la muestra en el nivel de Fermi tomada en la posición del centro de curvatura de una punta esféricamente simétrica ( modelo de punta de onda s ). Con tal simplificación, su modelo resultó valioso para interpretar imágenes de características de la superficie mayores que un nanómetro, aunque predijo corrugaciones a escala atómica de menos de un picómetro. Estas están muy por debajo del límite de detección del microscopio y por debajo de los valores realmente observados en los experimentos.

En experimentos con resolución subnanométrica, la convolución de los estados de la superficie de la punta y de la muestra siempre será importante, en la medida en que se observe una inversión aparente de las corrugaciones atómicas en el mismo barrido. Estos efectos solo se pueden explicar mediante el modelado de los estados electrónicos de la superficie y de la punta y las formas en que interactúan los dos electrodos a partir de principios básicos .

• 
  Islas de plata de un átomo de espesor cultivadas en terrazas de la superficie (111) del paladio. El tamaño de la imagen es de 250 nm por 250 nm.
• 
  Las franjas de reconstrucción características en la superficie (100) del oro tienen  un ancho de 1,44 nm ^[20] y consisten en seis filas atómicas que se ubican sobre cinco filas del volumen del cristal. El tamaño de la imagen es de aproximadamente 10 nm por 10 nm.
• 
  Una parte de 7 nm de largo de un nanotubo de carbono de pared simple .
• 
  Los átomos en la superficie de un cristal de carburo de silicio (SiC) están dispuestos en una red hexagonal y están separados por 0,3 nm.
• 
  Nanomanipulación STM de moléculas de PTCDA en grafito para inscribir el logotipo del Centro de Nanociencia (CeNS) de Múnich.

Un invento anterior similar al de Binnig y Rohrer, el Topografiner de R. Young, J. Ward y F. Scire del NIST , se basaba en la emisión de campo. ^[21] Sin embargo, el Comité Nobel reconoce a Young como la persona que se dio cuenta de que debería ser posible lograr una mejor resolución utilizando el efecto túnel. ^[22]

Se han desarrollado muchas otras técnicas de microscopía basadas en STM. Estas incluyen la microscopía de barrido de fotones (PSTM), que utiliza una punta óptica para tunelizar fotones; ^[4] potenciometría de efecto túnel de barrido (STP), que mide el potencial eléctrico a través de una superficie; ^[4] microscopía de efecto túnel de barrido con polarización de espín (SPSTM), que utiliza una punta ferromagnética para tunelizar electrones polarizados por espín en una muestra magnética; ^[23] microscopía de efecto túnel de barrido con múltiples puntas , que permite realizar mediciones eléctricas a escala nanométrica; y microscopía de fuerza atómica (AFM), en la que se mide la fuerza causada por la interacción entre la punta y la muestra.

El STM se puede utilizar para manipular átomos y cambiar la topografía de la muestra. Esto es atractivo por varias razones. En primer lugar, el STM tiene un sistema de posicionamiento atómicamente preciso, que permite una manipulación a escala atómica muy precisa. Además, después de modificar la superficie con la punta, el mismo instrumento se puede utilizar para obtener imágenes de las estructuras resultantes. Los investigadores de IBM desarrollaron una forma famosa de manipular átomos de xenón adsorbidos en una superficie de níquel . ^[4] Esta técnica se ha utilizado para crear corrales de electrones con una pequeña cantidad de átomos adsorbidos y observar oscilaciones de Friedel en la densidad de electrones en la superficie del sustrato. Además de modificar la superficie de la muestra real, también se puede utilizar el STM para tunelar electrones en una capa de fotorresistencia de haz de electrones en la muestra, para hacer litografía . Esto tiene la ventaja de ofrecer un mayor control de la exposición que la litografía de haz de electrones tradicional . Otra aplicación práctica del STM es la deposición atómica de metales (oro, plata, tungsteno, etc.) con cualquier patrón deseado (preprogramado), que pueden utilizarse como contactos para nanodispositivos o como nanodispositivos en sí mismos. ^{[ cita requerida ]}

Wikilibros tiene un libro sobre el tema: El manual de código abierto de nanociencia y nanotecnología

Wikimedia Commons alberga una categoría multimedia sobre Microscopio de efecto túnel .

• Un microscopio de efecto túnel de barrido filmado durante el funcionamiento con un microscopio electrónico.
• El funcionamiento interno de un STM: una explicación animada WeCanFigureThisOut.org
• Construya un STM simple con un costo de materiales inferior a $100 sin incluir el osciloscopio
• Animaciones y explicaciones sobre distintos tipos de microscopios, incluidos los microscopios electrónicos (Université Paris Sud)
• Introducción a la ciencia, la tecnología y la ingeniería en lenguaje sencillo (Universidad de Harvard)