Matriz (tipo de datos)

En informática , un array es un tipo de datos que representa una colección de elementos ( valores o variables ), cada uno seleccionado por uno o más índices (claves de identificación) que pueden calcularse en tiempo de ejecución durante la ejecución del programa. Este tipo de colección suele denominarse variable de matriz o valor de matriz . ^[1] Por analogía con los conceptos matemáticos vector y matriz , los tipos de matriz con uno y dos índices suelen denominarse tipo vector y tipo matriz , respectivamente. De forma más general, un tipo de matriz multidimensional puede denominarse tipo tensor , por analogía con el concepto físico tensor . ^[2]

El soporte del lenguaje para tipos de matriz puede incluir ciertos tipos de datos de matriz incorporados , algunas construcciones sintácticas ( constructores de tipo de matriz ) que el programador puede usar para definir dichos tipos y declarar variables de matriz, y notación especial para indexar elementos de matriz. ^[1] Por ejemplo, en el lenguaje de programación Pascal , la declaración type MyTable = array [1..4,1..2] of integer, define un nuevo tipo de datos de matriz llamado MyTable. La declaración var A: MyTableluego define una variable Ade ese tipo, que es un agregado de ocho elementos, cada uno de los cuales es una variable entera identificada por dos índices. En el programa Pascal, esos elementos se denotan A[1,1], A[1,2], A[2,1], …, A[4,2]. ^[3] Los tipos de matriz especiales a menudo se definen mediante las bibliotecas estándar del lenguaje .

Las listas dinámicas también son más comunes y más fáciles de implementar ^{[ dudoso – discutir ]} que las matrices dinámicas . Los tipos de matriz se distinguen de los tipos de registro principalmente porque permiten que los índices de los elementos se calculen en tiempo de ejecución , como en la asignación A[I,J] := A[N-I,2*J] de Pascal . Entre otras cosas, esta característica permite que una sola declaración iterativa procese arbitrariamente muchos elementos de una variable de matriz.

En contextos más teóricos, especialmente en la teoría de tipos y en la descripción de algoritmos abstractos , los términos "matriz" y "tipo de matriz" a veces se refieren a un tipo de datos abstracto (ADT) también llamado matriz abstracta o pueden referirse a una matriz asociativa , un modelo matemático con las operaciones básicas y el comportamiento de un tipo de matriz típico en la mayoría de los lenguajes: básicamente, una colección de elementos que se seleccionan mediante índices calculados en tiempo de ejecución.

Según el lenguaje, los tipos de matriz pueden superponerse (o identificarse con) otros tipos de datos que describen agregados de valores, como listas y cadenas . Los tipos de matriz suelen implementarse mediante estructuras de datos de matriz , pero a veces por otros medios, como tablas hash , listas enlazadas o árboles de búsqueda .

El lenguaje de programación Superplan (1949-1951) de Heinz Rutishauser incluía matrices multidimensionales. Sin embargo, aunque Rutishauser describió cómo se debía construir un compilador para su lenguaje, no lo implementó.

Los lenguajes ensambladores y los lenguajes de bajo nivel como BCPL ^[4] generalmente no tienen soporte sintáctico para matrices.

Debido a la importancia de las estructuras de matrices para un cálculo eficiente, los primeros lenguajes de programación de alto nivel, incluidos FORTRAN (1957), COBOL (1960) y Algol 60 (1960), proporcionaron soporte para matrices multidimensionales.

Una estructura de datos de matriz se puede modelar matemáticamente como una estructura de datos abstracta (una matriz abstracta ) con dos operaciones

obtener ( A , I ): los datos almacenados en el elemento de la matriz A cuyos índices son la tupla entera I .

conjunto ( A , I , V ): la matriz que resulta al establecer el valor de ese elemento en V .

Estas operaciones son necesarias para satisfacer los axiomas ^[5]

obtener ( establecer ( A , I , V ), I ) =  V

obtener ( conjunto ( A , I , V ), J ) =  obtener ( A , J ) si I  ≠  J

para cualquier estado de matriz A , cualquier valor V y cualquier tupla I , J para las que se definen las operaciones.

El primer axioma significa que cada elemento se comporta como una variable. El segundo axioma significa que los elementos con índices distintos se comportan como variables disjuntas , de modo que almacenar un valor en un elemento no afecta el valor de ningún otro elemento.

Estos axiomas no imponen ninguna restricción al conjunto de tuplas de índice válidas I , por lo tanto, este modelo abstracto se puede utilizar para matrices triangulares y otras matrices de formas irregulares.

Para implementar de manera efectiva variables de tipos tales como estructuras de matriz (con indexación realizada mediante aritmética de punteros ), muchos lenguajes restringen los índices a tipos de datos enteros ^{[6] [7]} (u otros tipos que se puedan interpretar como enteros, como bytes y tipos enumerados ), y requieren que todos los elementos tengan el mismo tipo de datos y tamaño de almacenamiento. La mayoría de esos lenguajes también restringen cada índice a un intervalo finito de números enteros, que permanece fijo durante la vida útil de la variable de matriz. De hecho, en algunos lenguajes compilados , es posible que los rangos de índice deban conocerse en el momento de la compilación .

Por otro lado, algunos lenguajes de programación proporcionan tipos de matriz más liberales, que permiten la indexación por valores arbitrarios, como números de punto flotante , cadenas , objetos , referencias , etc. Estos valores de índice no se pueden restringir a un intervalo, mucho menos a un intervalo fijo. Por lo tanto, estos lenguajes suelen permitir la creación de nuevos elementos arbitrarios en cualquier momento. Esta elección impide la implementación de tipos de matriz como estructuras de datos de matriz. Es decir, estos lenguajes utilizan una sintaxis similar a la de las matrices para implementar una semántica de matriz asociativa más general y, por lo tanto, deben implementarse mediante una tabla hash o alguna otra estructura de datos de búsqueda .

Esta sección no cita ninguna fuente . Por favor, ayude a mejorar esta sección añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado . ( Mayo de 2009 ) ( Aprenda cómo y cuándo eliminar este mensaje )

El número de índices necesarios para especificar un elemento se denomina dimensión , dimensionalidad o rango del tipo de matriz. (Esta nomenclatura entra en conflicto con el concepto de dimensión en álgebra lineal, que expresa la forma de una matriz . Por lo tanto, se dice que una matriz de números con 5 filas y 4 columnas, es decir, 20 elementos, tiene dimensión 2 en contextos informáticos, pero representa una matriz que se dice que tiene una dimensión de 4×5. Además, el significado de "rango" en informática entra en conflicto con la noción de rango tensorial , que es una generalización del concepto de álgebra lineal de rango de una matriz ).

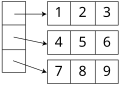
Muchos lenguajes sólo admiten matrices unidimensionales. En esos lenguajes, una matriz multidimensional se representa típicamente mediante un vector Iliffe , una matriz unidimensional de referencias a matrices de una dimensión menos. Una matriz bidimensional, en particular, se implementaría como un vector de punteros a sus filas. Por lo tanto, se accedería a un elemento en la fila i y la columna j de una matriz A mediante una doble indexación ( A [ i ][ j ] en la notación típica). Esta forma de emular matrices multidimensionales permite la creación de matrices escalonadas , donde cada fila puede tener un tamaño diferente o, en general, donde el rango válido de cada índice depende de los valores de todos los índices anteriores.

Esta representación para matrices multidimensionales es bastante común en el software C y C++. Sin embargo, C y C++ utilizarán una fórmula de indexación lineal para matrices multidimensionales que se declaren con un tamaño constante en tiempo de compilación, por ejemplo, mediante int A[10][20]o int A[m][n], en lugar del tradicional int **A. ^[8]

La mayoría de los lenguajes de programación que admiten matrices admiten las operaciones de almacenamiento y selección , y tienen una sintaxis especial para la indexación. Los primeros lenguajes usaban paréntesis, p. ej. A(i,j), como en FORTRAN; otros eligen corchetes, p. ej. A[i,j], o A[i][j], como en Algol 60 y Pascal (para distinguirlos del uso de paréntesis para llamadas a funciones ).

Los tipos de datos de matriz se implementan con mayor frecuencia como estructuras de matriz: con los índices restringidos a valores enteros (o totalmente ordenados), rangos de índices fijos en el momento de la creación de la matriz y direccionamiento de elementos multilineales. Este fue el caso en la mayoría de los lenguajes de "tercera generación" y sigue siendo el caso de la mayoría de los lenguajes de programación de sistemas como Ada , C y C++ . Sin embargo, en algunos lenguajes, los tipos de datos de matriz tienen la semántica de matrices asociativas, con índices de tipo arbitrario y creación de elementos dinámica. Este es el caso en algunos lenguajes de script como Awk y Lua , y de algunos tipos de matriz proporcionados por bibliotecas estándar de C++ .

Algunos lenguajes (como Pascal y Modula) realizan comprobaciones de límites en cada acceso, lanzando una excepción o cancelando el programa cuando algún índice está fuera de su rango válido. Los compiladores pueden permitir que se desactiven estas comprobaciones para sacrificar seguridad por velocidad. Otros lenguajes (como FORTRAN y C) confían en el programador y no realizan comprobaciones. Los buenos compiladores también pueden analizar el programa para determinar el rango de valores posibles que puede tener el índice, y este análisis puede llevar a la eliminación de la comprobación de límites .

Algunos lenguajes, como C, proporcionan únicamente tipos de matrices basados ​​en cero , para los cuales el valor mínimo válido para cualquier índice es 0. ^[9] Esta opción es conveniente para la implementación de matrices y los cálculos de direcciones. Con un lenguaje como C, se puede definir un puntero al interior de cualquier matriz que actuará simbólicamente como una pseudomatriz que admite índices negativos. Esto funciona únicamente porque C no verifica un índice con respecto a los límites cuando se utiliza.

Otros lenguajes sólo proporcionan tipos de matriz basados ​​en uno , donde cada índice comienza en 1; esta es la convención tradicional en matemáticas para matrices y secuencias matemáticas . Algunos lenguajes, como Pascal y Lua, admiten tipos de matriz basados ​​en n , cuyos índices legales mínimos son elegidos por el programador. Los méritos relativos de cada opción han sido objeto de un acalorado debate. La indexación basada en cero puede evitar errores de error de uno en uno o de postes de cerca . ^[10]

La relación entre los números que aparecen en la declaración de una matriz y el índice del último elemento de esa matriz también varía según el lenguaje. En muchos lenguajes (como C), se debe especificar el número de elementos que contiene la matriz; mientras que en otros (como Pascal y Visual Basic .NET ) se debe especificar el valor numérico del índice del último elemento. No hace falta decir que esta distinción es irrelevante en lenguajes donde los índices comienzan en 1, como Lua .

Algunos lenguajes de programación admiten la programación de matrices , donde las operaciones y funciones definidas para ciertos tipos de datos se extienden implícitamente a matrices de elementos de esos tipos. Por lo tanto, se puede escribir A + B para sumar los elementos correspondientes de dos matrices A y B. Por lo general, estos lenguajes proporcionan tanto la multiplicación elemento por elemento como el producto matricial estándar del álgebra lineal , y cuál de estos se representa mediante el operador * varía según el lenguaje.

Los lenguajes que ofrecen capacidades de programación de matrices han proliferado desde las innovaciones en esta área de APL . Estas son capacidades básicas de lenguajes específicos de dominio como GAUSS , IDL , Matlab y Mathematica . Son una característica básica de lenguajes más nuevos, como Julia y versiones recientes de Fortran . Estas capacidades también se proporcionan a través de bibliotecas de extensión estándar para otros lenguajes de programación de propósito general (como la biblioteca NumPy ampliamente utilizada para Python ).

Muchos lenguajes proporcionan un tipo de datos de cadena integrado , con notación especializada (" literales de cadena ") para construir valores de ese tipo. En algunos lenguajes (como C), una cadena es simplemente una matriz de caracteres, o se maneja de forma muy similar. Otros lenguajes, como Pascal , pueden proporcionar operaciones muy diferentes para cadenas y matrices.

Algunos lenguajes de programación proporcionan operaciones que devuelven el tamaño (número de elementos) de un vector o, de forma más general, el rango de cada índice de una matriz. En C y C++, las matrices no admiten la función de tamaño , por lo que los programadores a menudo tienen que declarar una variable independiente para almacenar el tamaño y pasarla a los procedimientos como un parámetro independiente.

Los elementos de una matriz recién creada pueden tener valores indefinidos (como en C) o pueden estar definidos para tener un valor "predeterminado" específico, como 0 o un puntero nulo (como en Java).

En C++, un objeto std::vector admite las operaciones store , select y append con las características de rendimiento que se mencionaron anteriormente. Se puede consultar el tamaño de los vectores y se puede cambiar su tamaño. También se admiten operaciones más lentas, como insertar un elemento en el medio.

Una operación de segmentación de matriz toma un subconjunto de los elementos de una entidad de tipo matriz (valor o variable) y luego los ensambla como otra entidad de tipo matriz, posiblemente con otros índices. Si los tipos de matriz se implementan como estructuras de matriz, se pueden realizar muchas operaciones de segmentación útiles (como seleccionar una submatriz, intercambiar índices o invertir la dirección de los índices) de manera muy eficiente manipulando el vector de referencia de la estructura. Las segmentaciones posibles dependen de los detalles de implementación: por ejemplo, FORTRAN permite segmentar una columna de una variable de matriz, pero no una fila, y tratarla como un vector; mientras que C permite segmentar una fila de una matriz, pero no una columna.

Por otro lado, son posibles otras operaciones de segmentación cuando los tipos de matriz se implementan de otras maneras.

Algunos lenguajes permiten matrices dinámicas (también llamadas redimensionables, ampliables o extensibles): variables de matriz cuyos rangos de índice pueden expandirse en cualquier momento después de su creación, sin cambiar los valores de sus elementos actuales.

Para matrices unidimensionales, esta función se puede proporcionar como una operación " append( A , x )" que aumenta el tamaño de la matriz A en uno y luego establece el valor del último elemento en x . Otros tipos de matrices (como las cadenas de Pascal) proporcionan un operador de concatenación, que se puede utilizar junto con la segmentación para lograr ese efecto y más. En algunos lenguajes, asignar un valor a un elemento de una matriz extiende automáticamente la matriz, si es necesario, para incluir ese elemento. En otros tipos de matrices, una segmentación se puede reemplazar por una matriz de diferente tamaño, y los elementos posteriores se renumeran en consecuencia, como en la asignación de lista de Python " A [5:5] = [10,20,30]", que inserta tres elementos nuevos (10,20 y 30) antes del elemento " A [5]". Las matrices redimensionables son conceptualmente similares a las listas , y los dos conceptos son sinónimos en algunos lenguajes.

Una matriz extensible se puede implementar como una matriz de tamaño fijo, con un contador que registra cuántos elementos están realmente en uso. La appendoperación simplemente incrementa el contador hasta que se utiliza toda la matriz, momento en el que la appendoperación puede definirse como fallida. Esta es una implementación de una matriz dinámica con una capacidad fija, como en el stringtipo de Pascal. Alternativamente, la appendoperación puede reasignar la matriz subyacente con un tamaño mayor y copiar los elementos antiguos en la nueva área.

• Análisis de acceso a matrices
• Sistema de gestión de bases de datos de matriz
• Eliminación de comprobación de límites
• Valores separados por delimitadores
• Comprobación de índice
• Matriz paralela
• Matriz dispersa
• Matriz de longitud variable

Wikilibros tiene un libro sobre el tema: Estructuras de datos/Matrices

Busque matriz en Wikcionario, el diccionario libre.

• Diccionario de algoritmos y estructuras de datos del NIST: matriz