Heterojunción
Interfaz entre dos capas o regiones de semiconductores diferentes

Una heterojunción es una interfaz entre dos capas o regiones de semiconductores diferentes . Estos materiales semiconductores tienen brechas de banda desiguales a diferencia de una homojunción . A menudo es ventajoso diseñar las bandas de energía electrónica en muchas aplicaciones de dispositivos de estado sólido, incluidos láseres semiconductores, células solares y transistores. La combinación de múltiples heterojunciones juntas en un dispositivo se denomina heteroestructura , aunque los dos términos se usan comúnmente de manera intercambiable. El requisito de que cada material sea un semiconductor con brechas de banda desiguales es algo laxo, especialmente en escalas de longitud pequeñas, donde las propiedades electrónicas dependen de propiedades espaciales. Una definición más moderna de heterojunción es la interfaz entre dos materiales de estado sólido, incluidas las estructuras cristalinas y amorfas de materiales metálicos, aislantes, conductores de iones rápidos y semiconductores.

Fabricación y aplicaciones

La fabricación de heterojunciones generalmente requiere el uso de epitaxia de haz molecular (MBE) [1] o tecnologías de deposición química en fase de vapor (CVD) para controlar con precisión el espesor de la deposición y crear una interfaz abrupta con una red perfectamente emparejada. Una alternativa reciente en investigación es el apilamiento mecánico de materiales en capas en heteroestructuras de van der Waals . [2]

A pesar de su costo, las heterojunciones han encontrado uso en una variedad de aplicaciones especializadas donde sus características únicas son críticas:

Catálisis : El uso de heterojunciones como fotocatalizador ha demostrado que exhiben un mejor desempeño en la fotorreducción de CO2 , producción de H2 y fotodegradación de contaminantes en agua que los óxidos de metal individuales. [8] El desempeño de la heterojunción se puede mejorar aún más mediante la incorporación de vacantes de oxígeno, ingeniería de facetas cristalinas o incorporación de materiales carbonosos.

Alineación de bandas de energía

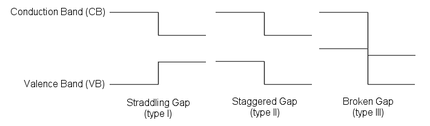
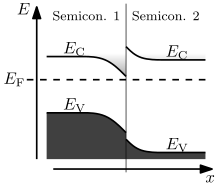
Los tres tipos de heterojunciones de semiconductores organizados por alineación de bandas.
Diagrama de bandas para heterojunción de semiconductores n - n en equilibrio.

El comportamiento de una unión semiconductora depende fundamentalmente de la alineación de las bandas de energía en la interfaz. Las interfaces semiconductoras se pueden organizar en tres tipos de heterojunciones: brecha a caballo (tipo I), brecha escalonada (tipo II) o brecha rota (tipo III), como se ve en la figura. [9] Lejos de la unión, la flexión de la banda se puede calcular con base en el procedimiento habitual de resolver la ecuación de Poisson .

Existen varios modelos para predecir la alineación de las bandas.

  • El modelo más simple (y menos preciso) es la regla de Anderson , que predice la alineación de las bandas basándose en las propiedades de las interfaces vacío-semiconductor (en particular, la afinidad electrónica del vacío ). La principal limitación es que no tiene en cuenta el enlace químico.
  • Se propuso una regla común para los aniones que supone que, dado que la banda de valencia está relacionada con los estados aniónicos, los materiales con los mismos aniones deberían tener desplazamientos de banda de valencia muy pequeños. Sin embargo, esto no explica los datos, sino que está relacionado con la tendencia de que dos materiales con diferentes aniones tienden a tener desplazamientos de banda de valencia mayores que desplazamientos de banda de conducción .
  • Tersoff [10] propuso un modelo de estado gap basado en uniones metal-semiconductor más conocidas , donde el desplazamiento de la banda de conducción está dado por la diferencia en la altura de la barrera Schottky . Este modelo incluye una capa dipolar en la interfaz entre los dos semiconductores que surge de la tunelización de electrones desde la banda de conducción de un material hacia el gap del otro (análogo a los estados gap inducidos por el metal ). Este modelo concuerda bien con sistemas donde ambos materiales están estrechamente emparejados en red [11], como GaAs / AlGaAs .
  • La regla 60:40 es una heurística para el caso específico de las uniones entre el semiconductor GaAs y el semiconductor de aleación Al x Ga 1− x As. A medida que la x en el lado Al x Ga 1− x As varía de 0 a 1, la relación tiende a mantener el valor 60/40. A modo de comparación, la regla de Anderson predice para una unión GaAs/AlAs ( x = 1). [12] [13] Δ mi do / Δ mi V {\displaystyle \Delta E_ {C}/\Delta E_ {V}} Δ mi do / Δ mi V = 0,73 / 0,27 {\displaystyle \Delta E_{C}/\Delta E_{V}=0,73/0,27}

El método típico para medir los desplazamientos de banda es calcularlos a partir de la medición de las energías de los excitones en los espectros de luminiscencia . [13]

Desajuste de masa efectivo

Cuando una heterojunción está formada por dos semiconductores diferentes , se puede fabricar un pozo cuántico debido a la diferencia en la estructura de bandas . Para calcular los niveles de energía estática dentro del pozo cuántico logrado, es sustancial comprender la variación o el desajuste de la masa efectiva a través de la heterojunción. El pozo cuántico definido en la heterojunción se puede tratar como un potencial de pozo finito con un ancho de . Además, en 1966, Conley et al. [14] y BenDaniel y Duke [15] informaron una condición de contorno para la función de envolvente en un pozo cuántico, conocida como condición de contorno de BenDaniel-Duke. Según ellos, la función de envolvente en un pozo cuántico fabricado debe satisfacer una condición de contorno que establece que y son ambos continuos en las regiones de interfaz. yo el Estilo de visualización l_{w}} ψ ( el ) {\displaystyle \psi(z)} 1 metro ∗ ∂ ∂ el ψ ( el ) {\displaystyle {\frac {1}{m^{*}}}{\partial \over {\partial z}}\psi (z)\,}

Detalles matemáticos resueltos para el ejemplo del pozo cuántico .

Utilizando la ecuación de Schrödinger para un pozo finito con ancho y centro en 0, la ecuación para el pozo cuántico logrado se puede escribir como: yo el Estilo de visualización l_{w}}

− ℏ 2 2 metro b ∗ d 2 ψ ( el ) d el 2 + V ψ ( el ) = mi ψ ( el )  para  el < − yo el 2 ( 1 ) {\displaystyle -{\frac {\hbar ^{2}}{2m_{b}^{*}}}{\frac {\mathrm {d} ^{2}\psi (z)}{\mathrm {d} z^{2}}}+V\psi (z)=E\psi (z)\quad \quad {\text{ para }}z<-{\frac {l_{w}}{2}}\quad \quad (1)}
− ℏ 2 2 metro el ∗ d 2 ψ ( el ) d el 2 = mi ψ ( el )  para  − yo el 2 < el < + yo el 2 ( 2 ) {\displaystyle \quad \quad -{\frac {\hbar ^{2}}{2m_{w}^{*}}}{\frac {\mathrm {d} ^{2}\psi (z)}{\mathrm {d} z^{2}}}=E\psi (z)\quad \quad {\text{ para }}-{\frac {l_{w}}{2}}<z<+{\frac {l_{w}}{2}}\quad \quad (2)}
− ℏ 2 2 metro b ∗ d 2 ψ ( el ) d el 2 + V ψ ( el ) = mi ψ ( el )  para  el > + yo el 2 ( 3 ) {\displaystyle -{\frac {\hbar ^{2}}{2m_{b}^{*}}}{\frac {\mathrm {d} ^{2}\psi (z)}{\mathrm {d} z^{2}}}+V\psi (z)=E\psi (z)\quad {\text{ para }}z>+{\frac {l_{w}}{2}}\quad \quad (3)}

Las soluciones de las ecuaciones anteriores son bien conocidas, solo que con diferentes k (modificadas) y [16] k {\estilo de visualización \kappa}

a = 2 metro el mi ℏ k = 2 metro b ( V − mi ) ℏ ( 4 ) {\displaystyle k={\frac {\sqrt {2m_{w}E}}{\hbar }}\quad \quad \kappa ={\frac {\sqrt {2m_{b}(VE)}}{\hbar }}\quad \quad (4)} .

En z = la solución de paridad par se puede obtener de + yo el 2 {\displaystyle +{\frac {l_{w}}{2}}}

A porque ⁡ ( a yo el 2 ) = B exp ⁡ ( − k yo el 2 ) ( 5 ) {\displaystyle A\cos({\frac {kl_{w}}{2}})=B\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (5)} .

Tomando la derivada de (5) y multiplicando ambos lados por 1 metro ∗ {\displaystyle {\frac {1}{m^{*}}}}

− a A metro el ∗ pecado ⁡ ( a yo el 2 ) = − k B metro b ∗ exp ⁡ ( − k yo el 2 ) ( 6 ) {\displaystyle -{\frac {kA}{m_{w}^{*}}}\sin({\frac {kl_{w}}{2}})=-{\frac {\kappa B}{m_{b}^{*}}}\exp(-{\frac {\kappa l_{w}}{2}})\quad \quad (6)} .

Dividiendo (6) por (5), se puede obtener la función solución de paridad par,

F ( mi ) = − a metro el ∗ broncearse ⁡ ( a yo el 2 ) − k metro b ∗ = 0 ( 7 ) {\displaystyle f(E)=-{\frac {k}{m_{w}^{*}}}\tan({\frac {kl_{w}}{2}})-{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (7)} .

De manera similar, para la solución de paridad impar,

F ( mi ) = − a metro el ∗ cuna ⁡ ( a yo el 2 ) + k metro b ∗ = 0 ( 8 ) {\displaystyle f(E)=-{\frac {k}{m_{w}^{*}}}\cot({\frac {kl_{w}}{2}})+{\frac {\kappa }{m_{b}^{*}}}=0\quad \quad (8)} .

Para la solución numérica , tomando las derivadas de (7) y (8) se obtiene

paridad uniforme:

d F d mi = 1 metro el ∗ d a d mi broncearse ⁡ ( a yo el 2 ) + a metro el ∗ segundo 2 ⁡ ( a yo el 2 ) × yo el 2 d a d mi − 1 metro b ∗ d k d mi ( 9 − 1 ) {\displaystyle {\frac {df}{dE}}={\frac {1}{m_{w}^{*}}}{\frac {dk}{dE}}\tan({\frac {kl_{ w}}{2}})+{\frac {k}{m_{w}^{*}}}\sec ^{2}({\frac {kl_{w}}{2}})\times { \frac {l_{w}}{2}}{\frac {dk}{dE}}-{\frac {1}{m_{b}^{*}}}{\frac {d\kappa }{dE }}\quad \quad (9-1)}

paridad impar:

d F d mi = 1 metro el ∗ d a d mi cuna ⁡ ( a yo el 2 ) − a metro el ∗ csc 2 ⁡ ( a yo el 2 ) × yo el 2 d a d mi + 1 metro b ∗ d k d mi ( 9 − 2 ) {\displaystyle {\frac {df}{dE}}={\frac {1}{m_{w}^{*}}}{\frac {dk}{dE}}\cot({\frac {kl_{ w}}{2}})-{\frac {k}{m_{w}^{*}}}\csc ^{2}({\frac {kl_{w}}{2}})\times { \frac {l_{w}}{2}}{\frac {dk}{dE}}+{\frac {1}{m_{b}^{*}}}{\frac {d\kappa }{dE }}\quad \quad (9-2)}

dónde . d a d mi = 2 metro el ∗ 2 mi ℏ d k d mi = − 2 metro b ∗ 2 V − mi ℏ {\displaystyle {\frac {dk}{dE}}={\frac {\sqrt {2m_{w}^{*}}}{2{\sqrt {E}}\hbar }}\quad \quad \quad {\frac {d\kappa }{dE}}=-{\frac {\sqrt {2m_{b}^{*}}}{2{\sqrt {VE}}\hbar }}}

La diferencia en masa efectiva entre materiales resulta en una diferencia mayor en las energías del estado fundamental .

Heterojunciones a escala nanométrica

Imagen de una heterojunción a escala nanométrica entre óxido de hierro (Fe 3 O 4  — esfera) y sulfuro de cadmio (CdS — varilla) tomada con un microscopio electrónico de transmisión ( TEM) . Esta unión desplazada de tipo II fue sintetizada por Hunter McDaniel y el Dr. Moonsub Shim en la Universidad de Illinois en Urbana-Champaign en 2007.

En los puntos cuánticos, las energías de banda dependen del tamaño del cristal debido a los efectos del tamaño cuántico . Esto permite la ingeniería de desplazamiento de banda en heteroestructuras a nanoescala. Es posible [17] utilizar los mismos materiales pero cambiar el tipo de unión, por ejemplo, de a horcajadas (tipo I) a escalonada (tipo II), modificando el tamaño o el espesor de los cristales involucrados. El sistema de heteroestructura a nanoescala más común es ZnS sobre CdSe (CdSe@ZnS) que tiene un desplazamiento de espacio a horcajadas (tipo I). En este sistema, el espacio de banda mucho más grande de ZnS pasiva la superficie del núcleo fluorescente de CdSe, aumentando así la eficiencia cuántica de la luminiscencia . Existe una ventaja adicional de mayor estabilidad térmica debido a los enlaces más fuertes en la capa de ZnS, como lo sugiere su mayor espacio de banda. Dado que tanto CdSe como ZnS crecen en la fase cristalina de blenda de zinc y están estrechamente emparejados en red, se prefiere el crecimiento del núcleo de la capa. En otros sistemas o bajo diferentes condiciones de crecimiento puede ser posible cultivar estructuras anisotrópicas como la que se ve en la imagen de la derecha.

La fuerza impulsora para la transferencia de carga entre bandas de conducción en estas estructuras es el desplazamiento de la banda de conducción. [18] Al disminuir el tamaño de los nanocristales de CdSe cultivados en TiO 2 , Robel et al. [18] descubrieron que los electrones se transferían más rápido desde la banda de conducción de CdSe más alta hacia TiO 2 . En CdSe, el efecto del tamaño cuántico es mucho más pronunciado en la banda de conducción debido a la menor masa efectiva que en la banda de valencia, y este es el caso de la mayoría de los semiconductores. En consecuencia, la ingeniería del desplazamiento de la banda de conducción suele ser mucho más fácil con heterojunciones a nanoescala. Para las heterojunciones a nanoescala desplazadas escalonadas (tipo II), puede ocurrir una separación de carga fotoinducida ya que allí el estado de energía más bajo para los huecos puede estar en un lado de la unión, mientras que la energía más baja para los electrones está en el lado opuesto. Se ha sugerido [18] que las heterojunciones a nanoescala escalonadas anisotrópicas (tipo II) se pueden utilizar para la fotocatálisis , específicamente para la división del agua con energía solar.

Véase también

Referencias

  1. ^ ab Smith, CG (1996). "Dispositivos cuánticos de baja dimensión". Rep. Prog. Phys. 59 (1996) 235282, pág. 244.
  2. ^ Geim, Alaska; Grigorieva, IV (2013). "Heteroestructuras de Van der Waals". Naturaleza . 499 (7459): 419–425. arXiv : 1307.6718 . doi : 10.1038/naturaleza12385. ISSN  0028-0836. PMID  23887427. S2CID  205234832.
  3. ^ Leu, Sylvère; Sontag, Detlef (2020), Shah, Arvind (ed.), "Células solares de silicio cristalino: células de heterojunción", Solar Cells and Modules , vol. 301, Cham: Springer International Publishing, págs. 163–195, doi :10.1007/978-3-030-46487-5_7, ISBN 978-3-030-46485-1, consultado el 18 de abril de 2023
  4. ^ Okuda, Koji; Okamoto, Hiroaki; Hamakawa, Yoshihiro (1983). "Célula solar apilada de Si amorfo/Si policristalino con una eficiencia de conversión superior al 12 %". Revista japonesa de física aplicada . 22 (9): L605–L607. Código Bibliográfico :1983JaJAP..22L.605O. doi :10.1143/JJAP.22.L605. S2CID  121569675.
  5. ^ Yamamoto, Kenji; Yoshikawa, Kunta; Uzu, Hisashi; Adachi, Daisuke (2018). "Células solares de silicio cristalino de heterojunción de alta eficiencia". Revista japonesa de física aplicada . 57 (8S3): 08RB20. Código Bibliográfico :2018JaJAP..57hRB20Y. doi :10.7567/JJAP.57.08RB20. S2CID  125265042.
  6. ^ "HJT - Células solares de heterojunción". Paneles solares . Consultado el 25 de marzo de 2022 .
  7. ^ Kroemer, H. (1963). "Una clase propuesta de láseres de inyección de heterounión". Actas del IEEE . 51 (12): 1782–1783. doi :10.1109/PROC.1963.2706.
  8. ^ Ortiz-Quiñonez, Jose-Luis; Pal, Umapada (octubre de 2024). "Nanoestructuras de heterojunción de óxido metálico diseñadas mediante interfaz en la reducción fotocatalítica de CO2: progreso y perspectivas". Coordination Chemistry Reviews . 516 : 215967. doi : 10.1016/j.ccr.2024.215967 .
  9. ^ Ihn, Thomas (2010). "cap. 5.1 Ingeniería de bandas". Semiconductor Nanostructures Quantum States and Electronic Transport . Estados Unidos de América: Oxford University Press. pp. 66. ISBN 9780199534432.
  10. ^ J. Tersoff (1984). "Teoría de las heterojunciones de semiconductores: el papel de los dipolos cuánticos". Physical Review B . 30 (8): 4874–4877. Código Bibliográfico :1984PhRvB..30.4874T. doi :10.1103/PhysRevB.30.4874.
  11. ^ Pallab, Bhattacharya (1997), Dispositivos optoelectrónicos semiconductores, Prentice Hall, ISBN 0-13-495656-7 
  12. ^ Adachi, Sadao (1 de enero de 1993). Propiedades del arseniuro de galio y aluminio. ISBN 9780852965580.
  13. ^ ab Debbar, N.; Biswas, Dipankar; Bhattacharya, Pallab (1989). "Desplazamientos de la banda de conducción en pozos cuánticos pseudomórficos InxGa1-xAs/Al0.2Ga0.8As (0,07≤x≤0,18) medidos mediante espectroscopia transitoria de nivel profundo". Physical Review B . 40 (2): 1058–1063. Bibcode :1989PhRvB..40.1058D. doi :10.1103/PhysRevB.40.1058. PMID  9991928.
  14. ^ Conley, J.; Duke, C.; Mahan, G.; Tiemann, J. (1966). "Efectos túnel de electrones en barreras metal-semiconductoras". Physical Review . 150 (2): 466. Bibcode :1966PhRv..150..466C. doi :10.1103/PhysRev.150.466.
  15. ^ Bendaniel, D.; Duke, C. (1966). "Efectos de la carga espacial en el efecto túnel de electrones". Physical Review . 152 (2): 683. Bibcode :1966PhRv..152..683B. doi :10.1103/PhysRev.152.683.
  16. ^ Griffiths, David J. (2004). Introducción a la mecánica cuántica (2.ª edición). Prentice Hall. ISBN 0-13-111892-7 
  17. ^ Ivanov, Sergei A.; Piryatinski, Andrei; Nanda, Jagjit; Tretiak, Sergei; Zavadil, Kevin R.; Wallace, William O.; Werder, Don; Klimov, Victor I. (2007). "Nanocristales de CdS/ZnSe de núcleo/capa de tipo II: síntesis, estructuras electrónicas y propiedades espectroscópicas". Revista de la Sociedad Química Estadounidense . 129 (38): 11708–19. doi :10.1021/ja068351m. PMID  17727285.
  18. ^ abc Robel, István; Kuno, Masaru; Kamat, Prashant V. (2007). "Inyección de electrones dependiente del tamaño a partir de puntos cuánticos de CdSe excitados en nanopartículas de TiO2". Revista de la Sociedad Química Estadounidense . 129 (14): 4136–7. doi :10.1021/ja070099a. PMID  17373799.

Lectura adicional

  • Bastard, Gérald (1991). Mecánica ondulatoria aplicada a heteroestructuras de semiconductores . Wiley-Interscience . ISBN 978-0-470-21708-5.
  • Feucht, D. Lion; Milnes, AG (1970). Heterojunciones y uniones metal-semiconductoras . Nueva York y Londres : Academic Press ., ISBN 0-12-498050-3 . Una referencia algo anticuada con respecto a las aplicaciones, pero siempre una buena introducción a los principios básicos de los dispositivos de heterojunción. 
  • R. Tsu; F. Zypman (1990). "Nuevos conocimientos sobre la física del efecto túnel resonante". Surface Science . 228 (1–3): 418. Bibcode :1990SurSc.228..418T. doi :10.1016/0039-6028(90)90341-5.
  • Kurhekar, Anil Sudhakar (2018). "El recocido térmico mejora las propiedades eléctricas del diodo de heterounión". Conferencia internacional sobre investigación y educación en energías renovables (Rere-2018) . Actas de la conferencia AIP. Vol. 1992. pág. 040027. Código Bibliográfico :2018AIPC.1992d0027K. doi :10.1063/1.5047992.
Obtenido de "https://es.wikipedia.org/w/index.php?title=Heterojunción&oldid=1242312935"