Resonancia

Este artículo tiene varios problemas. Ayúdenos a mejorarlo o a discutir estos problemas en la página de discusión . ( Aprenda cómo y cuándo eliminar estos mensajes ) La sección introductoria de este artículo puede ser demasiado breve para resumir adecuadamente los puntos clave .Considere ampliar la introducción para proporcionar una descripción general accesible de todos los aspectos importantes del artículo. ( Enero de 2021 ) Este artículo está escrito como un artículo de investigación o una revista científica .Por favor, ayude a mejorar el artículo reescribiéndolo en estilo enciclopédico y simplificando las frases demasiado técnicas . ( Enero de 2023 )( Aprenda cómo y cuándo eliminar este mensaje ) Este artículo necesita citas adicionales para su verificación . Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Resonance" – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this message) ... (Learn how and when to remove this message)

En física, la resonancia se refiere a una amplia clase de fenómenos que surgen como resultado de la coincidencia de períodos temporales o espaciales de objetos oscilatorios. Para un sistema dinámico oscilatorio impulsado por una fuerza externa que varía en el tiempo , la resonancia ocurre cuando la frecuencia de la fuerza externa coincide con la frecuencia natural del sistema. ^[3] La resonancia puede ocurrir en varios sistemas, como sistemas mecánicos, eléctricos o acústicos, y es deseable en ciertas aplicaciones, como instrumentos musicales o receptores de radio. La resonancia también puede ser indeseable, lo que lleva a vibraciones excesivas o incluso fallas estructurales en algunos casos.

Todos los sistemas, incluidos los sistemas moleculares y las partículas, tienden a vibrar a una frecuencia natural que depende de su estructura; esta frecuencia se conoce como frecuencia resonante o frecuencia de resonancia . Cuando se aplica una fuerza oscilante , una vibración externa, a una frecuencia resonante de un sistema dinámico, un objeto o una partícula, la vibración externa hará que el sistema oscile a una amplitud mayor (con más fuerza) que cuando se aplica la misma fuerza a otras frecuencias no resonantes. ^[4]

Las frecuencias de resonancia de un sistema se pueden identificar cuando la respuesta a una vibración externa crea una amplitud que es un máximo relativo dentro del sistema. ^[4] Pequeñas fuerzas periódicas que están cerca de una frecuencia de resonancia del sistema tienen la capacidad de producir oscilaciones de gran amplitud en el sistema debido al almacenamiento de energía vibracional .

Los fenómenos de resonancia se producen con todo tipo de vibraciones u ondas : existe la resonancia mecánica , la resonancia orbital , la resonancia acústica , la resonancia electromagnética , la resonancia magnética nuclear (RMN), la resonancia de espín electrónico (ESR) y la resonancia de funciones de onda cuánticas . Los sistemas resonantes se pueden utilizar para generar vibraciones de una frecuencia específica (por ejemplo, instrumentos musicales ) o para seleccionar frecuencias específicas de una vibración compleja que contenga muchas frecuencias (por ejemplo, filtros).

El término resonancia (del latín resonantia , 'eco', de resonare , 'resonar') se originó en el campo de la acústica, particularmente en la resonancia simpática observada en los instrumentos musicales, por ejemplo, cuando una cuerda comienza a vibrar y producir sonido después de que se golpea otra diferente.

La resonancia se produce cuando un sistema es capaz de almacenar y transferir fácilmente energía entre dos o más modos de almacenamiento diferentes (como la energía cinética y la energía potencial en el caso de un péndulo simple). Sin embargo, hay algunas pérdidas de ciclo a ciclo, llamadas amortiguamiento . Cuando el amortiguamiento es pequeño, la frecuencia de resonancia es aproximadamente igual a la frecuencia natural del sistema, que es una frecuencia de vibraciones no forzadas. Algunos sistemas tienen múltiples frecuencias de resonancia distintas.

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (February 2024) (Learn how and when to remove this message)

Un ejemplo conocido es el columpio de un patio de recreo , que actúa como un péndulo . Si se empuja a una persona en un columpio al ritmo del intervalo natural del columpio (su frecuencia de resonancia), el columpio se eleva cada vez más (amplitud máxima), mientras que los intentos de empujar el columpio a un ritmo más rápido o más lento producen arcos más pequeños. ^{[5] : p.2–24} Esto se debe a que la energía que absorbe el columpio se maximiza cuando los empujones coinciden con las oscilaciones naturales del columpio.

La resonancia se produce ampliamente en la naturaleza y se aprovecha en muchos dispositivos. Es el mecanismo por el cual se generan prácticamente todas las ondas y vibraciones sinusoidales . Por ejemplo, cuando se golpean objetos duros como el metal , el vidrio o la madera , se producen breves vibraciones resonantes en el objeto. ^{[5] : p.2–24} La luz y otras radiaciones electromagnéticas de longitud de onda corta se producen por resonancia a escala atómica , como los electrones en los átomos. Otros ejemplos de resonancia incluyen:

• Mecanismos de cronometraje de relojes y relojes modernos, por ejemplo, el volante en un reloj mecánico y el cristal de cuarzo en un reloj de cuarzo.
• Resonancia de las mareas en la bahía de Fundy
• Resonancias acústicas de los instrumentos musicales y del tracto vocal humano
• Rotura de una copa de cristal al ser expuesta a un tono musical del tono adecuado (su frecuencia de resonancia)
• Idiófonos de fricción , como hacer vibrar un objeto de vidrio (vaso, botella, jarrón) frotando su borde con la punta de un dedo.
• Resonancia eléctrica de circuitos sintonizados en radios y televisores que permiten recibir frecuencias de radio de forma selectiva
• Creación de luz coherente por resonancia óptica en una cavidad láser
• Resonancia orbital ejemplificada por algunas lunas de los planetas gigantes del Sistema Solar y grupos resonantes como los plutinos.
• Las resonancias materiales a escala atómica son la base de varias técnicas espectroscópicas que se utilizan en la física de la materia condensada.
  • Resonancia de espín electrónico
  • Efecto Mössbauer
  • Resonancia magnética nuclear

La resonancia se manifiesta en muchos sistemas lineales y no lineales como oscilaciones alrededor de un punto de equilibrio. Cuando el sistema es impulsado por una entrada externa sinusoidal, una salida medida del sistema puede oscilar en respuesta. La relación entre la amplitud de las oscilaciones de estado estable de la salida y las oscilaciones de la entrada se denomina ganancia, y la ganancia puede ser una función de la frecuencia de la entrada externa sinusoidal. Los picos de la ganancia en ciertas frecuencias corresponden a resonancias, donde la amplitud de las oscilaciones de la salida medida son desproporcionadamente grandes.

Dado que muchos sistemas lineales y no lineales que oscilan se modelan como osciladores armónicos cerca de sus equilibrios, se muestra una derivación de la frecuencia de resonancia para un oscilador armónico amortiguado y excitado. Se utiliza un circuito RLC para ilustrar las conexiones entre la resonancia y la función de transferencia, la respuesta de frecuencia, los polos y los ceros de un sistema. A partir del ejemplo del circuito RLC, se generalizan estas conexiones para sistemas lineales de orden superior con múltiples entradas y salidas.

Consideremos una masa amortiguada sobre un resorte impulsada por una fuerza sinusoidal aplicada externamente. La segunda ley de Newton toma la forma

$${\displaystyle m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=F_{0}\sin(\omega t)-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}},}$$

( 1 )

donde m es la masa, x es el desplazamiento de la masa desde el punto de equilibrio, F ₀ es la amplitud de impulso, ω es la frecuencia angular de impulso, k es la constante del resorte y c es el coeficiente de amortiguamiento viscoso. Esto se puede reescribir en la forma

$${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {F_{0}}{m}}\sin(\omega t),}$$

( 2 )

dónde

• ${\textstyle \omega _{0}={\sqrt {k/m}}}$se llama frecuencia angular no amortiguada del oscilador o frecuencia natural ,
• ${\displaystyle \zeta ={\frac {c}{2{\sqrt {mk}}}}}$se llama relación de amortiguamiento .

Muchas fuentes también se refieren a ω ₀ como la frecuencia de resonancia . Sin embargo, como se muestra a continuación, al analizar las oscilaciones del desplazamiento x ( t ), la frecuencia de resonancia es cercana pero no igual a ω ₀ . En general, la frecuencia de resonancia es cercana pero no necesariamente igual a la frecuencia natural. ^[6] El ejemplo de circuito RLC en la siguiente sección da ejemplos de diferentes frecuencias de resonancia para el mismo sistema.

La solución general de la ecuación ( 2 ) es la suma de una solución transitoria que depende de las condiciones iniciales y una solución de estado estable que es independiente de las condiciones iniciales y depende únicamente de la amplitud de excitación F ₀ , la frecuencia de excitación ω , la frecuencia angular no amortiguada ω ₀ y la relación de amortiguamiento ζ . La solución transitoria decae en un tiempo relativamente corto, por lo que para estudiar la resonancia es suficiente considerar la solución de estado estable.

Es posible escribir la solución de estado estable para x ( t ) como una función proporcional a la fuerza impulsora con un cambio de fase inducido φ ,

$${\displaystyle x(t)={\frac {F_{0}}{m{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}}\sin(\omega t+\varphi ),}$$

( 3 )

dónde${\displaystyle \varphi =\arctan \left({\frac {2\omega \omega _{0}\zeta }{\omega ^{2}-\omega _{0}^{2}}}\right)+n\pi .}$

El valor de la fase generalmente se considera entre −180° y 0, por lo que representa un desfase de fase tanto para los valores positivos como negativos del argumento arctan.

La resonancia se produce cuando, a ciertas frecuencias de excitación, la amplitud de estado estable de x ( t ) es grande en comparación con su amplitud a otras frecuencias de excitación. Para la masa de un resorte, la resonancia corresponde físicamente a las oscilaciones de la masa que tienen grandes desplazamientos desde la posición de equilibrio del resorte a ciertas frecuencias de excitación. Si observamos la amplitud de x ( t ) como una función de la frecuencia de excitación ω , la amplitud es máxima en la frecuencia de excitación$${\displaystyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.}$$

ω _r es la frecuencia de resonancia de este sistema. Nuevamente, la frecuencia de resonancia no es igual a la frecuencia angular no amortiguada ω ₀ del oscilador. Son proporcionales y, si la relación de amortiguamiento tiende a cero, son las mismas, pero para un amortiguamiento distinto de cero, no son la misma frecuencia. Como se muestra en la figura, la resonancia también puede ocurrir en otras frecuencias cercanas a la frecuencia de resonancia, incluida ω ₀ , pero la respuesta máxima se da en la frecuencia de resonancia.

Además, ω _r solo es real y distinto de cero si , por lo que este sistema solo puede resonar cuando el oscilador armónico está significativamente subamortiguado. Para sistemas con una relación de amortiguamiento muy pequeña y una frecuencia de excitación cercana a la frecuencia de resonancia, las oscilaciones en estado estacionario pueden llegar a ser muy grandes.${\textstyle \zeta <1/{\sqrt {2}}}$

Para otros osciladores armónicos amortiguados y accionados cuyas ecuaciones de movimiento no se parecen exactamente a la masa de un resorte, la frecuencia de resonancia permanece pero las definiciones de ω ₀ y ζ cambian según la física del sistema. Para un péndulo de longitud ℓ y un ángulo de desplazamiento pequeño θ , la ecuación ( 1 ) se convierte en$${\displaystyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}},}$$$${\displaystyle m\ell {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}=F_{0}\sin(\omega t)-mg\theta -c\ell {\frac {\mathrm {d} \theta }{\mathrm {d} t}}}$$

y por lo tanto

• ${\displaystyle \omega _{0}={\sqrt {\frac {g}{\ell }}},}$
• ${\displaystyle \zeta ={\frac {c}{2m}}{\sqrt {\frac {\ell }{g}}}.}$

This section may be too long and excessively detailed. Please consider summarizing the material. (January 2021)

Considere un circuito que consta de una resistencia con resistencia R , un inductor con inductancia L y un capacitor con capacitancia C conectados en serie con corriente i ( t ) y accionados por una fuente de voltaje con voltaje v _in ( t ). La caída de voltaje alrededor del circuito es

${\displaystyle L{\frac {di(t)}{dt}}+Ri(t)+V(0)+{\frac {1}{C}}\int _{0}^{t}i(\tau )d\tau =v_{\text{in}}(t).}$

( 4 )

En lugar de analizar una solución candidata para esta ecuación como en el ejemplo de masa en un resorte anterior, esta sección analizará la respuesta de frecuencia de este circuito. Tomando la transformada de Laplace de la ecuación ( 4 ), donde I ( s ) y V _in ( s ) son la transformada de Laplace de la corriente y el voltaje de entrada, respectivamente, y s es un parámetro de frecuencia complejo en el dominio de Laplace. Reordenando los términos,$${\displaystyle sLI(s)+RI(s)+{\frac {1}{sC}}I(s)=V_{\text{in}}(s),}$$$${\displaystyle I(s)={\frac {s}{s^{2}L+Rs+{\frac {1}{C}}}}V_{\text{in}}(s).}$$

Un circuito RLC en serie presenta varias opciones para medir el voltaje de salida. Supongamos que el voltaje de salida de interés es la caída de voltaje en el capacitor. Como se muestra arriba, en el dominio de Laplace este voltaje es o$${\displaystyle V_{\text{out}}(s)={\frac {1}{sC}}I(s)}$$$${\displaystyle V_{\text{out}}={\frac {1}{LC(s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}})}}V_{\text{in}}(s).}$$

Defina para este circuito una frecuencia natural y una relación de amortiguamiento,$${\displaystyle \omega _{0}={\frac {1}{\sqrt {LC}}},}$$$${\displaystyle \zeta ={\frac {R}{2}}{\sqrt {\frac {C}{L}}}.}$$

La relación entre el voltaje de salida y el voltaje de entrada se convierte en$${\displaystyle H(s)\triangleq {\frac {V_{\text{out}}(s)}{V_{\text{in}}(s)}}={\frac {\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}}$$

H ( s ) es la función de transferencia entre el voltaje de entrada y el voltaje de salida. Esta función de transferencia tiene dos polos (raíces del polinomio en el denominador de la función de transferencia) en

$${\displaystyle s=-\zeta \omega _{0}\pm i\omega _{0}{\sqrt {1-\zeta ^{2}}}}$$

( 5 )

y no hay ceros-raíces del polinomio en el numerador de la función de transferencia. Además, para ζ ≤ 1 , la magnitud de estos polos es la frecuencia natural ω ₀ y que para ζ < 1/${\displaystyle {\sqrt {2}}}$ , nuestra condición para la resonancia en el ejemplo del oscilador armónico, los polos están más cerca del eje imaginario que del eje real.

Evaluando H ( s ) a lo largo del eje imaginario s = iω , la función de transferencia describe la respuesta de frecuencia de este circuito. De manera equivalente, la respuesta de frecuencia se puede analizar tomando la transformada de Fourier de la ecuación ( 4 ) en lugar de la transformada de Laplace. La función de transferencia, que también es compleja, se puede escribir como una ganancia y una fase,$${\displaystyle H(i\omega )=G(\omega )e^{i\Phi (\omega )}.}$$

Un voltaje de entrada sinusoidal a una frecuencia ω da como resultado un voltaje de salida a la misma frecuencia que ha sido escalado por G ( ω ) y tiene un desplazamiento de fase Φ ( ω ). La ganancia y la fase se pueden representar gráficamente en función de la frecuencia en un diagrama de Bode . Para el voltaje del capacitor del circuito RLC, la ganancia de la función de transferencia H ( iω ) es

$${\displaystyle G(\omega )={\frac {\omega _{0}^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.}$$

( 6 )

Nótese la similitud entre la ganancia aquí y la amplitud en la ecuación ( 3 ). Una vez más, la ganancia se maximiza en la frecuencia resonante.$${\displaystyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.}$$

Aquí, la resonancia corresponde físicamente a tener una amplitud relativamente grande para las oscilaciones de estado estable del voltaje a través del capacitor en comparación con su amplitud en otras frecuencias de activación.

La frecuencia de resonancia no siempre tiene que adoptar la forma indicada en los ejemplos anteriores. Para el circuito RLC, supongamos que el voltaje de salida de interés es el voltaje a través del inductor. Como se muestra arriba, en el dominio de Laplace el voltaje a través del inductor es$${\displaystyle V_{\text{out}}(s)=sLI(s),}$$$${\displaystyle V_{\text{out}}(s)={\frac {s^{2}}{s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}}}V_{\text{in}}(s),}$$$${\displaystyle V_{\text{out}}(s)={\frac {s^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}V_{\text{in}}(s),}$$

utilizando las mismas definiciones para ω ₀ y ζ que en el ejemplo anterior. La función de transferencia entre V _in ( s ) y esta nueva V _out ( s ) a través del inductor es$${\displaystyle H(s)={\frac {s^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.}$$

Esta función de transferencia tiene los mismos polos que la función de transferencia del ejemplo anterior, pero también tiene dos ceros en el numerador en s = 0. Al evaluar H ( s ) a lo largo del eje imaginario, su ganancia se convierte en$${\displaystyle G(\omega )={\frac {\omega ^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.}$$

En comparación con la ganancia en la ecuación ( 6 ) que utiliza el voltaje del capacitor como salida, esta ganancia tiene un factor de ω ² en el numerador y, por lo tanto, tendrá una frecuencia de resonancia diferente que maximiza la ganancia. Esa frecuencia es$${\displaystyle \omega _{r}={\frac {\omega _{0}}{\sqrt {1-2\zeta ^{2}}}},}$$

Por lo tanto, para el mismo circuito RLC pero con el voltaje a través del inductor como salida, la frecuencia de resonancia es ahora mayor que la frecuencia natural, aunque todavía tiende hacia la frecuencia natural a medida que la relación de amortiguamiento tiende a cero. Que el mismo circuito pueda tener diferentes frecuencias de resonancia para diferentes opciones de salida no es contradictorio. Como se muestra en la ecuación ( 4 ), la caída de voltaje a través del circuito se divide entre los tres elementos del circuito, y cada elemento tiene una dinámica diferente. El voltaje del capacitor crece lentamente al integrar la corriente a lo largo del tiempo y, por lo tanto, es más sensible a frecuencias más bajas, mientras que el voltaje del inductor crece cuando la corriente cambia rápidamente y, por lo tanto, es más sensible a frecuencias más altas. Si bien el circuito en su conjunto tiene una frecuencia natural en la que tiende a oscilar, la dinámica diferente de cada elemento del circuito hace que cada elemento resuene a una frecuencia ligeramente diferente.

Supongamos que el voltaje de salida de interés es el voltaje a través del resistor. En el dominio de Laplace, el voltaje a través del resistor es$${\displaystyle V_{\text{out}}(s)=RI(s),}$$$${\displaystyle V_{\text{out}}(s)={\frac {Rs}{L\left(s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}\right)}}V_{\text{in}}(s),}$$

y utilizando la misma frecuencia natural y relación de amortiguamiento que en el ejemplo del capacitor, la función de transferencia es$${\displaystyle H(s)={\frac {2\zeta \omega _{0}s}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.}$$

Esta función de transferencia también tiene los mismos polos que los ejemplos de circuitos RLC anteriores, pero solo tiene un cero en el numerador en s = 0. Para esta función de transferencia, su ganancia es$${\displaystyle G(\omega )={\frac {2\zeta \omega _{0}\omega }{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.}$$

La frecuencia de resonancia que maximiza esta ganancia es y la ganancia es uno en esta frecuencia, por lo que el voltaje a través de la resistencia resuena en la frecuencia natural del circuito y en esta frecuencia la amplitud del voltaje a través de la resistencia es igual a la amplitud del voltaje de entrada.$${\displaystyle \omega _{r}=\omega _{0},}$$

Algunos sistemas presentan antirresonancia, que se puede analizar de la misma manera que la resonancia. En el caso de la antirresonancia, la amplitud de la respuesta del sistema a ciertas frecuencias es desproporcionadamente pequeña en lugar de ser desproporcionadamente grande. En el ejemplo del circuito RLC, este fenómeno se puede observar analizando tanto el inductor como el condensador en conjunto.

Supongamos que el voltaje de salida de interés en el circuito RLC es el voltaje a través del inductor y el capacitor combinados en serie. La ecuación ( 4 ) mostró que la suma de los voltajes a través de los tres elementos del circuito suma el voltaje de entrada, por lo que medir el voltaje de salida como la suma de los voltajes del inductor y el capacitor combinados es lo mismo que v _in menos la caída de voltaje a través del resistor. El ejemplo anterior mostró que a la frecuencia natural del sistema, la amplitud de la caída de voltaje a través del resistor es igual a la amplitud de v _in y, por lo tanto, el voltaje a través del inductor y el capacitor combinados tiene amplitud cero. Podemos demostrar esto con la función de transferencia.

La suma de los voltajes del inductor y del capacitor es$${\displaystyle V_{\text{out}}(s)=(sL+{\frac {1}{sC}})I(s),}$$$${\displaystyle V_{\text{out}}(s)={\frac {s^{2}+{\frac {1}{LC}}}{s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}}}V_{\text{in}}(s).}$$

Utilizando la misma frecuencia natural y las mismas razones de amortiguamiento que en los ejemplos anteriores, la función de transferencia es$${\displaystyle H(s)={\frac {s^{2}+\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.}$$

Esta transferencia tiene los mismos polos que los ejemplos anteriores pero tiene ceros en

$${\displaystyle s=\pm i\omega _{0}.}$$

( 7 )

Evaluando la función de transferencia a lo largo del eje imaginario, su ganancia es$${\displaystyle G(\omega )={\frac {\omega _{0}^{2}-\omega ^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.}$$

En lugar de buscar resonancia, es decir, picos de la ganancia, observe que la ganancia llega a cero en ω = ω ₀ , lo que complementa nuestro análisis del voltaje de la resistencia. Esto se llama antiresonancia , que tiene el efecto opuesto a la resonancia. En lugar de dar como resultado salidas que son desproporcionadamente grandes en esta frecuencia, este circuito con esta elección de salida no tiene respuesta en absoluto en esta frecuencia. La frecuencia que se filtra corresponde exactamente a los ceros de la función de transferencia, que se mostraron en la ecuación ( 7 ) y estaban en el eje imaginario.

Estos ejemplos de circuitos RLC ilustran cómo se relaciona la resonancia con la respuesta de frecuencia del sistema. En concreto, estos ejemplos ilustran:

• Cómo se pueden encontrar frecuencias resonantes buscando picos en la ganancia de la función de transferencia entre la entrada y la salida del sistema, por ejemplo en un diagrama de magnitud de Bode
• Cómo la frecuencia de resonancia de un solo sistema puede ser diferente para diferentes opciones de salida del sistema
• La conexión entre la frecuencia natural del sistema, la relación de amortiguamiento del sistema y la frecuencia de resonancia del sistema.
• La conexión entre la frecuencia natural del sistema y la magnitud de los polos de la función de transferencia, señalada en la Ecuación ( 5 ), y por lo tanto una conexión entre los polos y la frecuencia de resonancia.
• Una conexión entre los ceros de la función de transferencia y la forma de la ganancia en función de la frecuencia y, por lo tanto, una conexión entre los ceros y la frecuencia de resonancia que maximiza la ganancia.
• Una conexión entre los ceros de la función de transferencia y la antiresonancia

La siguiente sección extiende estos conceptos a la resonancia en un sistema lineal general.

Consideremos ahora un sistema lineal arbitrario con múltiples entradas y salidas. Por ejemplo, en la representación en el espacio de estados, un sistema lineal invariante en el tiempo de tercer orden con tres entradas y dos salidas podría escribirse como donde u _i ( t ) son las entradas, x _i ( t ) son las variables de estado, y _i ( t ) son las salidas y A , B , C y D son matrices que describen la dinámica entre las variables.$${\displaystyle {\begin{bmatrix}{\dot {x}}_{1}\\{\dot {x}}_{2}\\{\dot {x}}_{3}\end{bmatrix}}=A{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\x_{3}(t)\end{bmatrix}}+B{\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\u_{3}(t)\end{bmatrix}},}$$$${\displaystyle {\begin{bmatrix}y_{1}(t)\\y_{2}(t)\end{bmatrix}}=C{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\x_{3}(t)\end{bmatrix}}+D{\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\u_{3}(t)\end{bmatrix}},}$$

Este sistema tiene una matriz de funciones de transferencia cuyos elementos son las funciones de transferencia entre las distintas entradas y salidas. Por ejemplo,$${\displaystyle {\begin{bmatrix}Y_{1}(s)\\Y_{2}(s)\end{bmatrix}}={\begin{bmatrix}H_{11}(s)&H_{12}(s)&H_{13}(s)\\H_{21}(s)&H_{22}(s)&H_{23}(s)\end{bmatrix}}{\begin{bmatrix}U_{1}(s)\\U_{2}(s)\\U_{3}(s)\end{bmatrix}}.}$$

Cada H _ij ( s ) es una función de transferencia escalar que vincula una de las entradas con una de las salidas. Los ejemplos de circuitos RLC anteriores tenían un voltaje de entrada y mostraban cuatro voltajes de salida posibles (a través del capacitor, a través del inductor, a través del resistor y a través del capacitor y el inductor combinados en serie), cada uno con su propia función de transferencia. Si el circuito RLC se configurara para medir los cuatro voltajes de salida, ese sistema tendría una matriz de función de transferencia de 4 × 1 que vincula la entrada única con cada una de las cuatro salidas.

Evaluado a lo largo del eje imaginario, cada H _ij ( iω ) puede escribirse como una ganancia y un desplazamiento de fase,$${\displaystyle H_{ij}(i\omega )=G_{ij}(\omega )e^{i\Phi _{ij}(\omega )}.}$$

Los picos de ganancia en ciertas frecuencias corresponden a resonancias entre la entrada y la salida de esa función de transferencia, asumiendo que el sistema es estable .

Cada función de transferencia H _ij ( s ) también puede escribirse como una fracción cuyo numerador y denominador son polinomios de s .$${\displaystyle H_{ij}(s)={\frac {N_{ij}(s)}{D_{ij}(s)}}.}$$

Las raíces complejas del numerador se llaman ceros, y las raíces complejas del denominador se llaman polos. Para un sistema estable, las posiciones de estos polos y ceros en el plano complejo dan alguna indicación de si el sistema puede resonar o antiresonar y en qué frecuencias. En particular, cualquier par de polos conjugados complejos, estables o marginalmente estables , con componentes imaginarios se puede escribir en términos de una frecuencia natural y una relación de amortiguamiento como en la ecuación ( 5 ). La frecuencia natural ω ₀ de ese polo es la magnitud de la posición del polo en el plano complejo y la relación de amortiguamiento de ese polo determina qué tan rápido decae esa oscilación. En general, ^[6]$${\displaystyle s=-\zeta \omega _{0}\pm i\omega _{0}{\sqrt {1-\zeta ^{2}}},}$$

• Los pares complejos conjugados de polos cerca del eje imaginario corresponden a un pico o resonancia en la respuesta de frecuencia en la proximidad de la frecuencia natural del polo. Si el par de polos está en el eje imaginario, la ganancia es infinita en esa frecuencia.
• Los pares complejos conjugados de ceros cerca del eje imaginario corresponden a una muesca o antirresonancia en la respuesta de frecuencia en la proximidad de la frecuencia del cero, es decir, la frecuencia igual a la magnitud del cero. Si el par de ceros está en el eje imaginario, la ganancia es cero en esa frecuencia.

En el ejemplo del circuito RLC, la primera generalización que relaciona los polos con la resonancia se observa en la ecuación ( 5 ). La segunda generalización que relaciona los ceros con la antiresonancia se observa en la ecuación ( 7 ). En los ejemplos del oscilador armónico, la tensión del condensador del circuito RLC y la tensión del inductor del circuito RLC, los "polos cerca del eje imaginario" corresponden a la condición significativamente subamortiguada ζ < 1/ .${\displaystyle {\sqrt {2}}}$

Un sistema físico puede tener tantas frecuencias naturales como grados de libertad y puede resonar cerca de cada una de esas frecuencias naturales. Una masa en un resorte, que tiene un grado de libertad, tiene una frecuencia natural. Un péndulo doble , que tiene dos grados de libertad, puede tener dos frecuencias naturales. A medida que aumenta el número de osciladores armónicos acoplados, el tiempo que lleva transferir energía de uno al siguiente se vuelve significativo. Los sistemas con un número muy grande de grados de libertad pueden considerarse continuos en lugar de tener osciladores discretos. ^{[ cita requerida ]}

La energía se transfiere de un oscilador al siguiente en forma de ondas. Por ejemplo, la cuerda de una guitarra o la superficie del agua en un recipiente se pueden modelar como un continuo de pequeños osciladores acoplados y las ondas pueden viajar a lo largo de ellos. En muchos casos, estos sistemas tienen el potencial de resonar a ciertas frecuencias, formando ondas estacionarias con oscilaciones de gran amplitud en posiciones fijas. La resonancia en forma de ondas estacionarias subyace a muchos fenómenos familiares, como el sonido producido por los instrumentos musicales, las cavidades electromagnéticas utilizadas en láseres y hornos microondas, y los niveles de energía de los átomos. ^{[ cita requerida ]}

Cuando se hace funcionar una cuerda de longitud fija a una frecuencia determinada, una onda se propaga a lo largo de la cuerda a la misma frecuencia. Las ondas se reflejan en los extremos de la cuerda y, finalmente, se alcanza un estado estable con ondas que viajan en ambas direcciones. La forma de onda es la superposición de las ondas. ^[7]

En determinadas frecuencias, la forma de onda de estado estable no parece desplazarse a lo largo de la cuerda. En posiciones fijas llamadas nodos , la cuerda nunca se desplaza . Entre los nodos, la cuerda oscila y exactamente a mitad de camino entre los nodos (en posiciones llamadas antinodos) las oscilaciones tienen su mayor amplitud. ^{[8] [9] [10]}

Para una cuerda de longitud con extremos fijos, el desplazamiento de la cuerda perpendicular al eje en el tiempo es ^[7]${\displaystyle L}$${\displaystyle y(x,t)}$${\displaystyle x}$${\displaystyle t}$$${\displaystyle y(x,t)=2y_{\text{max}}\sin(kx)\cos(2\pi ft),}$$

dónde

• ${\displaystyle y_{\text{max}}}$es la amplitud de las ondas que viajan hacia la izquierda y hacia la derecha que interfieren para formar la onda estacionaria,
• ${\displaystyle k}$es el número de onda ,
• ${\displaystyle f}$es la frecuencia .

Las frecuencias que resuenan y forman ondas estacionarias se relacionan con la longitud de la cuerda como ^{[11] [9]}$${\displaystyle f={\frac {nv}{2L}},}$$$${\displaystyle n=1,2,3,\dots }$$

donde es la velocidad de la onda y el entero denota diferentes modos o armónicos . La onda estacionaria con n = 1 oscila a la frecuencia fundamental y tiene una longitud de onda que es el doble de la longitud de la cuerda. Los posibles modos de oscilación forman una serie armónica . ^[11]${\displaystyle v}$${\displaystyle n}$

Una generalización a redes complejas de osciladores armónicos acoplados muestra que tales sistemas tienen un número finito de frecuencias resonantes naturales, relacionadas con la estructura topológica de la red misma. En particular, tales frecuencias resultan relacionadas con los valores propios de la matriz laplaciana de la red. Sea la matriz de adyacencia que describe la estructura topológica de la red y la matriz laplaciana correspondiente , donde es la matriz diagonal de los grados de los nodos de la red. Entonces, para una red de osciladores armónicos clásicos e idénticos, cuando se aplica una fuerza impulsora sinusoidal a un nodo específico, las frecuencias resonantes globales de la red están dadas por donde son los valores propios del laplaciano . ^[12]${\displaystyle {\bf {A}}}$${\displaystyle {\bf {L}}={\bf {K}}-{\bf {A}}}$${\displaystyle {\bf {K}}={\rm {diag}}\,\{k_{i}\}}$${\displaystyle f(t)=F_{0}\sin \omega t}$${\displaystyle \omega _{i}={\sqrt {1+\mu _{i}}}}$${\displaystyle \mu _{i}}$${\displaystyle {\bf {L}}}$

La resonancia mecánica es la tendencia de un sistema mecánico a absorber más energía cuando la frecuencia de sus oscilaciones coincide con la frecuencia natural de vibración del sistema que con otras frecuencias. Puede provocar movimientos violentos de balanceo e incluso fallas catastróficas en estructuras construidas incorrectamente, incluidos puentes, edificios, trenes y aviones. Al diseñar objetos, los ingenieros deben asegurarse de que las frecuencias de resonancia mecánica de los componentes no coincidan con las frecuencias vibratorias de los motores u otras piezas oscilantes, un fenómeno conocido como desastre por resonancia .

Evitar los desastres por resonancia es una preocupación importante en todos los proyectos de construcción de edificios, torres y puentes . Como contramedida, se pueden instalar soportes amortiguadores para absorber las frecuencias de resonancia y, de este modo, disipar la energía absorbida. El edificio Taipei 101 se basa en un péndulo de 660 toneladas (730 toneladas cortas), un amortiguador de masa sintonizado , para cancelar la resonancia. Además, la estructura está diseñada para resonar a una frecuencia que no se produce normalmente. Los edificios en zonas sísmicas suelen construirse para tener en cuenta las frecuencias oscilantes del movimiento del suelo esperado . Además, los ingenieros que diseñan objetos que tienen motores deben asegurarse de que las frecuencias resonantes mecánicas de los componentes no coincidan con las frecuencias vibratorias de accionamiento de los motores u otras piezas que oscilan fuertemente.

Los relojes marcan el tiempo mediante resonancia mecánica en un volante , un péndulo o un cristal de cuarzo .

Se ha planteado la hipótesis de que la cadencia de los corredores es energéticamente favorable debido a la resonancia entre la energía elástica almacenada en la extremidad inferior y la masa del corredor. ^[13]

La resonancia acústica es una rama de la resonancia mecánica que estudia las vibraciones mecánicas en el rango de frecuencias de la audición humana, es decir, el sonido . Para los humanos, la audición normalmente se limita a frecuencias entre aproximadamente 20  Hz y 20 000 Hz (20  kHz ), ^[14] Muchos objetos y materiales actúan como resonadores con frecuencias resonantes dentro de este rango y, cuando se golpean, vibran mecánicamente, empujando el aire circundante para crear ondas sonoras. Esta es la fuente de muchos sonidos de percusión que escuchamos.

La resonancia acústica es una consideración importante para los constructores de instrumentos, ya que la mayoría de los instrumentos acústicos utilizan resonadores , como las cuerdas y el cuerpo de un violín , la longitud del tubo de una flauta y la forma y la tensión de la membrana de un tambor.

Al igual que la resonancia mecánica, la resonancia acústica puede provocar una falla catastrófica del objeto en resonancia. El ejemplo clásico de esto es romper una copa de vino con un sonido a la frecuencia de resonancia precisa del vidrio, aunque esto es difícil en la práctica. ^[15]

Los motores de cohetes de la Estación Espacial Internacional (ISS) están controlados por un piloto automático . Normalmente, los parámetros cargados para controlar el sistema de control de motores del módulo Zvezda hacen que los motores de cohetes impulsen la Estación Espacial Internacional a una órbita más alta. Los motores de cohetes están montados sobre bisagras y, normalmente, la tripulación no se da cuenta de su funcionamiento. Sin embargo, el 14 de enero de 2009, los parámetros cargados hicieron que el piloto automático hiciera oscilar los motores de cohetes en oscilaciones cada vez más grandes, a una frecuencia de 0,5 Hz. Estas oscilaciones se capturaron en video y duraron 142 segundos. ^[16]

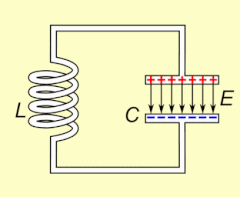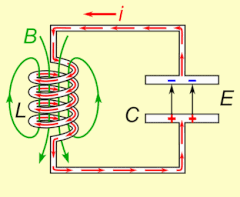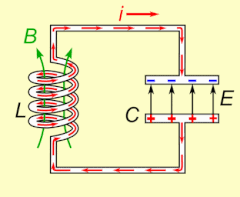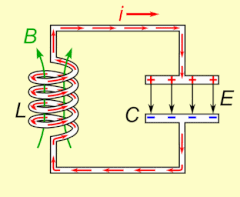
La resonancia eléctrica se produce en un circuito eléctrico a una frecuencia de resonancia determinada cuando la impedancia del circuito es mínima en un circuito en serie o máxima en un circuito en paralelo (normalmente cuando la función de transferencia alcanza su valor absoluto máximo). La resonancia en los circuitos se utiliza tanto para transmitir como para recibir comunicaciones inalámbricas, como la televisión, los teléfonos móviles y la radio.

Una cavidad óptica , también llamada resonador óptico , es una disposición de espejos que forma un resonador de cavidad de onda estacionaria para ondas de luz . Las cavidades ópticas son un componente principal de los láseres , rodeando el medio de ganancia y proporcionando retroalimentación de la luz láser. También se utilizan en osciladores paramétricos ópticos y algunos interferómetros . La luz confinada en la cavidad se refleja varias veces produciendo ondas estacionarias para ciertas frecuencias resonantes. Los patrones de ondas estacionarias producidos se denominan "modos". Los modos longitudinales difieren solo en frecuencia, mientras que los modos transversales difieren para diferentes frecuencias y tienen diferentes patrones de intensidad a lo largo de la sección transversal del haz. Los resonadores de anillo y las galerías susurrantes son ejemplos de resonadores ópticos que no forman ondas estacionarias.

Los distintos tipos de resonadores se distinguen por las distancias focales de los dos espejos y la distancia entre ellos; los espejos planos no se suelen utilizar debido a la dificultad de alinearlos con precisión. La geometría (tipo de resonador) debe elegirse de forma que el haz se mantenga estable, es decir, que el tamaño del haz no siga creciendo con cada reflexión. Los tipos de resonadores también están diseñados para cumplir otros criterios, como la cintura mínima del haz o la ausencia de un punto focal (y, por lo tanto, de una luz intensa en ese punto) dentro de la cavidad.

Las cavidades ópticas están diseñadas para tener un factor Q muy grande . ^[17] Un haz se refleja una gran cantidad de veces con poca atenuación ; por lo tanto, el ancho de la línea de frecuencia del haz es pequeño en comparación con la frecuencia del láser.

Otras resonancias ópticas son las resonancias de modo guiado y la resonancia de plasmón de superficie , que dan lugar a una reflexión anómala y a campos evanescentes elevados en la resonancia. En este caso, los modos resonantes son los modos guiados de una guía de ondas o los modos de plasmón de superficie de una interfaz dieléctrica-metálica. Estos modos suelen estar excitados por una rejilla de sublongitud de onda.

En mecánica celeste , una resonancia orbital ocurre cuando dos cuerpos en órbita ejercen una influencia gravitatoria periódica y regular entre sí, generalmente debido a que sus períodos orbitales están relacionados por una relación de dos enteros pequeños. Las resonancias orbitales mejoran en gran medida la influencia gravitatoria mutua de los cuerpos. En la mayoría de los casos, esto da como resultado una interacción inestable , en la que los cuerpos intercambian momento y cambian órbitas hasta que la resonancia ya no existe. En algunas circunstancias, un sistema resonante puede ser estable y autocorrector, de modo que los cuerpos permanecen en resonancia. Algunos ejemplos son la resonancia 1:2:4 de las lunas de Júpiter , Ganimedes , Europa e Ío , y la resonancia 2:3 entre Plutón y Neptuno . Las resonancias inestables con las lunas interiores de Saturno dan lugar a huecos en los anillos de Saturno . El caso especial de resonancia 1:1 (entre cuerpos con radios orbitales similares) hace que los grandes cuerpos del Sistema Solar despejen el vecindario alrededor de sus órbitas expulsando casi todo lo demás que los rodea; este efecto se utiliza en la definición actual de planeta .

La resonancia magnética nuclear (RMN) es el nombre que se le da a un fenómeno de resonancia física que implica la observación de propiedades magnéticas mecánicas cuánticas específicas de un núcleo atómico en presencia de un campo magnético externo aplicado. Muchas técnicas científicas explotan los fenómenos de RMN para estudiar la física molecular , los cristales y los materiales no cristalinos mediante espectroscopia de RMN . La RMN también se utiliza de forma rutinaria en técnicas avanzadas de imágenes médicas, como la resonancia magnética (IRM).

Todos los núcleos que contienen un número impar de nucleones tienen un momento magnético y un momento angular intrínsecos . Una característica clave de la RMN es que la frecuencia de resonancia de una sustancia particular es directamente proporcional a la fuerza del campo magnético aplicado. Esta característica es la que se aprovecha en las técnicas de obtención de imágenes; si una muestra se coloca en un campo magnético no uniforme, las frecuencias de resonancia de los núcleos de la muestra dependen de dónde se encuentren en el campo. Por lo tanto, la partícula se puede localizar con bastante precisión por su frecuencia de resonancia.

La resonancia paramagnética electrónica , también conocida como resonancia de espín electrónico (ESR), es una técnica espectroscópica similar a la RMN, pero utiliza electrones desapareados. Los materiales a los que se puede aplicar son mucho más limitados, ya que el material debe tener un espín desapareado y ser paramagnético .

El efecto Mössbauer es la emisión y absorción resonante y sin retroceso de fotones de rayos gamma por átomos unidos en forma sólida.

La resonancia en la física de partículas aparece en circunstancias similares a las de la física clásica en el nivel de la mecánica cuántica y la teoría cuántica de campos . Las resonancias también pueden considerarse partículas inestables, y la fórmula de la sección Curva de resonancia universal de este artículo se aplica si Γ es la tasa de desintegración de la partícula y Ω es la masa de la partícula M. En ese caso, la fórmula proviene del propagador de la partícula , con su masa reemplazada por el número complejo M  +  iΓ . La fórmula está relacionada además con la tasa de desintegración de la partícula mediante el teorema óptico .

Una columna de soldados marchando a paso regular sobre un puente estrecho y estructuralmente flexible puede provocar oscilaciones de amplitud peligrosamente grandes . El 12 de abril de 1831, el puente colgante de Broughton, cerca de Salford, Inglaterra , se derrumbó mientras un grupo de soldados británicos marchaba por él. ^[18] Desde entonces, el ejército británico ha tenido una orden permanente para que los soldados rompan el paso al marchar por puentes, para evitar que la resonancia de su patrón de marcha regular afecte al puente. ^{[19] [20]}

Las vibraciones de un motor pueden inducir vibraciones resonantes en las estructuras que lo sostienen si su frecuencia natural es cercana a la de las vibraciones del motor. Un ejemplo común es el sonido de traqueteo de la carrocería de un autobús cuando el motor se deja en ralentí.

La resonancia estructural de un puente colgante inducida por el viento puede provocar su colapso catastrófico. Varios puentes colgantes antiguos en Europa y Estados Unidos fueron destruidos por resonancia estructural inducida por vientos moderados. El colapso del puente Tacoma Narrows el 7 de noviembre de 1940 se caracteriza en física como un ejemplo clásico de resonancia. ^[21] Robert H. Scanlan y otros han argumentado que la destrucción fue causada por un aleteo aeroelástico , una interacción complicada entre el puente y los vientos que pasan a través de él, un ejemplo de autooscilación o una especie de "vibración autosostenida" como se hace referencia en la teoría no lineal de vibraciones. ^[22]

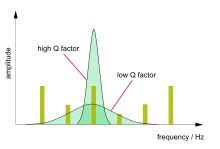
El factor Q o factor de calidad es un parámetro adimensional que describe cuán poco amortiguado está un oscilador o resonador, y caracteriza el ancho de banda de un resonador en relación con su frecuencia central. ^{[23] [24]} Un valor alto de Q indica una tasa menor de pérdida de energía en relación con la energía almacenada, es decir, el sistema está ligeramente amortiguado. El parámetro se define mediante la ecuación: . ^[25]$${\displaystyle Q=2\pi {\text{ }}{\frac {\text{ maximum energy stored}}{\text{total energy lost per cycle at resonance}}}}$$

Cuanto mayor sea el factor Q, mayor será la amplitud en la frecuencia de resonancia y menor el ancho de banda o rango de frecuencias alrededor de la resonancia. En resonancia eléctrica, un circuito de alto Q en un receptor de radio es más difícil de sintonizar, pero tiene mayor selectividad y, por lo tanto, sería mejor para filtrar señales de otras estaciones. Los osciladores de alto Q son más estables. ^[25]

Entre los ejemplos que normalmente tienen un factor Q bajo se encuentran los cierrapuertas (Q=0,5). Entre los sistemas con factores Q altos se encuentran los diapasones (Q=1000), los relojes atómicos y los láseres (Q≈10 ¹¹ ). ^[26]

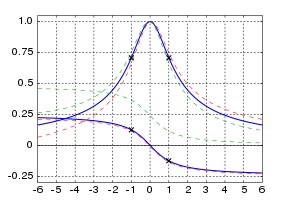
La respuesta exacta de una resonancia, especialmente para frecuencias alejadas de la frecuencia resonante, depende de los detalles del sistema físico y, por lo general, no es exactamente simétrica respecto de la frecuencia resonante, como se ilustra para el oscilador armónico simple anterior.

Para un oscilador lineal ligeramente amortiguado con una frecuencia de resonancia , la intensidad de las oscilaciones cuando el sistema se activa con una frecuencia de activación se aproxima típicamente mediante la siguiente fórmula que es simétrica respecto de la frecuencia de resonancia: ^[27]${\displaystyle \omega _{0}}$${\displaystyle I}$${\displaystyle \omega }$$${\displaystyle I(\omega )\equiv |\chi |^{2}\propto {\frac {1}{(\omega -\omega _{0})^{2}+\left({\frac {\Gamma }{2}}\right)^{2}}}.}$$

Donde la susceptibilidad vincula la amplitud del oscilador a la fuerza impulsora en el espacio de frecuencia: ^[28]${\displaystyle \chi (\omega )}$$${\displaystyle x(\omega )=\chi (\omega )F(\omega )}$$

La intensidad se define como el cuadrado de la amplitud de las oscilaciones. Se trata de una función de Lorentz o distribución de Cauchy , y esta respuesta se encuentra en muchas situaciones físicas que involucran sistemas resonantes. Γ es un parámetro que depende de la amortiguación del oscilador y se conoce como el ancho de línea de la resonancia. Los osciladores fuertemente amortiguados tienden a tener anchos de línea amplios y responden a un rango más amplio de frecuencias de excitación alrededor de la frecuencia resonante. El ancho de línea es inversamente proporcional al factor Q , que es una medida de la agudeza de la resonancia.

En ingeniería de radio e ingeniería electrónica , esta respuesta simétrica aproximada se conoce como curva de resonancia universal , un concepto introducido por Frederick E. Terman en 1932 para simplificar el análisis aproximado de circuitos de radio con un rango de frecuencias centrales y valores Q. ^{[29] [30]}

• Aspelmeyer, M ; Kippenberg, Tobias J.; Marquardt, Florian (30 de diciembre de 2014). "Optomecánica de cavidades" . Reviews of Modern Physics . 86 (4): 1391. arXiv : 1303.0733 . Bibcode :2014RvMP...86.1391A. doi :10.1103/RevModPhys.86.1391. hdl :11858/00-001M-0000-002D-6464-3. S2CID  119252645.
• Billah, K. Yusuf; Scanlan, Robert H (1991). "Resonancia, falla del puente de Tacoma Narrows y libros de texto de física para estudiantes de grado" (PDF) . American Journal of Physics . 59 (2): 118–124. Bibcode :1991AmJPh..59..118B. doi :10.1119/1.16590. Archivado (PDF) desde el original el 2000-09-19 . Consultado el 1 de enero de 2021 .
• Ghatak, Ajoy (2005). Óptica (3ª ed.). Nueva Delhi: Tata McGraw-Hill. ISBN 978-0-07-058583-6.
• Halliday, David ; Resnick, Robert ; Walker, Jearl (2005). Fundamentos de física . Vol. Parte 2 (7.ª ed.). John Wiley & Sons Ltd. ISBN 978-0-471-71716-4.
• Hardt, David (2004). "Understanding Poles and Zeros" (PDF) . 2.14 Análisis y diseño de sistemas de control por retroalimentación . Instituto Tecnológico de Massachusetts . Archivado (PDF) desde el original el 2022-10-09 . Consultado el 18 de abril de 2020 .
• Harlow, James H., ed. (2004). Ingeniería de transformadores de potencia eléctrica. Londres: CRC Press. ISBN 978-0-8493-1704-0.
• Ogata, Katsuhiko (2005). Dinámica de sistemas (4ª ed.). Harlow: Pearson. ISBN 978-1-292-02608-4.
• Olson, Harry F. (1967). Música, física e ingeniería . Vol. 2. Nueva York: Dover Publications. ISBN. 978-0-486-21769-7.
• Serway, Raymond A.; Faughn, Jerry S. (1992). Física universitaria (3.ª ed.). Saunders College Publishing. ISBN 0-03-076377-0.
• Siebert, William McC. (1986). Circuitos, señales y sistemas. Londres; Nueva York: MIT Press' McGraw Hill Book Company. ISBN 978-0-262-19229-3.
• Siegman, AE (1986). Láseres . Libros de ciencias universitarias. ISBN 978-0-935702-11-8.
• Snyder, Kristine L.; Farley, Claire T. (2011). "Frecuencia de zancada energéticamente óptima al correr: los efectos de la inclinación y la inclinación". The Journal of Experimental Biology . 214 (12): 2089–2095. doi : 10.1242/jeb.053157 . PMID  21613526.
• Terman, Frederick Emmons (1932). Ingeniería de radio (1.ª ed.). Nueva York: McGraw-Hill Book Company. OCLC  1036819790.
• Tooley, Michael H. (2006). Circuitos electrónicos: fundamentos y aplicaciones . Oxford: Taylor & Francis. ISBN 978-0-7506-6923-8.

Wikimedia Commons alberga una categoría multimedia sobre Resonancia .

• Las conferencias de física de Feynman, vol. I, cap. 23: Resonancia
• Resonancia Archivado el 3 de enero de 2017 en Wayback Machine - un capítulo de un libro de texto en línea
• Greene, Brian , “ Resonancia en cuerdas ”. El universo elegante , NOVA ( PBS )
• Sección de hiperfísica sobre conceptos de resonancia
• Resonancia versus resonante (uso de términos)
• Resonancia de la madera y del aire en un clavicémbalo
• Subprograma Java que muestra resonancias en una cuerda cuando varía la frecuencia de la fuerza impulsora
• Subprograma Java que demuestra la aparición de resonancia cuando la frecuencia de activación coincide con la frecuencia natural de un oscilador
• Rompiendo cristales con sonido Archivado el 2 de diciembre de 2008 en Wayback Machine , incluye imágenes a alta velocidad de cristales rotos