Estructura causal

En física matemática , la estructura causal de una variedad lorentziana describe las relaciones causales entre puntos de la variedad.

En la física moderna (especialmente en la relatividad general ) , el espacio-tiempo se representa mediante una variedad lorentziana . Las relaciones causales entre los puntos de la variedad se interpretan como una descripción de qué eventos en el espacio-tiempo pueden influir en otros eventos.

La estructura causal de una variedad lorentziana arbitraria (posiblemente curva) se complica por la presencia de curvatura . Los análisis de la estructura causal de dichas variedades deben formularse en términos de curvas suaves que unen pares de puntos. Las condiciones sobre los vectores tangentes de las curvas definen entonces las relaciones causales.

Si es una variedad lorentziana (para métricas en la variedad ), entonces los vectores tangentes distintos de cero en cada punto de la variedad se pueden clasificar en tres tipos disjuntos . Un vector tangente es:${\displaystyle \,(M,g)}$ ${\estilo de visualización g}$ ${\estilo de visualización M}$${\estilo de visualización X}$

• como si fuera temporal${\displaystyle \,g(X,X)<0}$
• nulo o similar a la luz si${\displaystyle \,g(X,X)=0}$
• como el espacio si${\displaystyle \,g(X,X)>0}$

Aquí utilizamos la signatura métrica . Decimos que un vector tangente no es espacial si es nulo o temporal.${\displaystyle (-,+,+,+,\cpuntos)}$

La variedad lorentziana canónica es el espacio-tiempo de Minkowski , donde y es la métrica plana de Minkowski . Los nombres de los vectores tangentes provienen de la física de este modelo. Las relaciones causales entre puntos en el espacio-tiempo de Minkowski toman una forma particularmente simple porque el espacio tangente también es y, por lo tanto, los vectores tangentes pueden identificarse con puntos en el espacio. El vector de cuatro dimensiones se clasifica de acuerdo con el signo de , donde es una coordenada cartesiana en el espacio tridimensional, es la constante que representa el límite de velocidad universal y es el tiempo. La clasificación de cualquier vector en el espacio será la misma en todos los marcos de referencia que estén relacionados por una transformación de Lorentz (pero no por una transformación general de Poincaré porque el origen puede desplazarse) debido a la invariancia de la métrica.${\displaystyle M=\mathbb {R} ^{4}}$${\estilo de visualización g}$ ${\displaystyle \mathbb {R} ^{4}}$${\displaystyle X=(t,r)}$${\displaystyle g(X,X)=-c^{2}t^{2}+\|r\|^{2}}$${\displaystyle r\in \mathbb {R} ^{3}}$${\estilo de visualización c}$${\estilo de visualización t}$

En cada punto del espacio tangente temporal, los vectores tangentes del punto se pueden dividir en dos clases. Para ello, definimos primero una relación de equivalencia en pares de vectores tangentes temporales.${\estilo de visualización M}$

Si y son dos vectores tangentes temporales en un punto decimos que y son equivalentes (escritos ) si .${\estilo de visualización X}$${\estilo de visualización Y}$${\estilo de visualización X}$${\estilo de visualización Y}$${\displaystyle X\sim Y}$${\displaystyle \,g(X,Y)<0}$

Existen entonces dos clases de equivalencia que contienen entre ellas todos los vectores tangentes temporales en el punto. Podemos (arbitrariamente) llamar a una de estas clases de equivalencia dirigida al futuro y a la otra dirigida al pasado . Físicamente, esta designación de las dos clases de vectores temporales dirigidos al futuro y al pasado corresponde a la elección de una flecha del tiempo en el punto. Las designaciones dirigidas al futuro y al pasado se pueden extender a vectores nulos en un punto por continuidad.

Una variedad lorentziana es orientable en el tiempo ^[1] si se puede hacer una designación continua de vectores no espaciales dirigidos hacia el futuro y hacia el pasado sobre toda la variedad.

Un camino en es una función continua donde es un intervalo no degenerado (es decir, un conjunto conectado que contiene más de un punto) en . Un camino suave tiene diferenciable una cantidad apropiada de veces (normalmente ), y un camino regular tiene derivada no nula.${\estilo de visualización M}$${\displaystyle \mu :\Sigma \to M}$${\estilo de visualización \Sigma}$${\displaystyle \mathbb {R}}$${\estilo de visualización \mu}$${\displaystyle C^{\infty}}$

Una curva en es la imagen de un camino o, más propiamente, una clase de equivalencia de imágenes de caminos relacionadas por re-parametrización, es decir, homeomorfismos o difeomorfismos de . Cuando es orientable en el tiempo, la curva está orientada si se requiere que el cambio de parámetro sea monótono .${\estilo de visualización M}$${\estilo de visualización \Sigma}$${\estilo de visualización M}$

Las curvas (o trayectorias) regulares suaves se pueden clasificar según sus vectores tangentes. Una curva de este tipo es${\estilo de visualización M}$

• cronológico (o temporal ) si el vector tangente es temporal en todos los puntos de la curva. También se denomina línea del mundo . ^[2]
• nulo si el vector tangente es nulo en todos los puntos de la curva.
• espacial si el vector tangente es espacial en todos los puntos de la curva.
• causal (o no espacial ) si el vector tangente es temporal o nulo en todos los puntos de la curva.

Los requisitos de regularidad y no degeneración garantizan que las curvas causales cerradas (como las que consisten en un único punto) no sean admitidas automáticamente por todos los espacio-tiempos.${\estilo de visualización \Sigma}$

Si la variedad es orientable en el tiempo, entonces las curvas no espaciales pueden clasificarse además dependiendo de su orientación con respecto al tiempo.

Una curva cronológica, nula o causal en es${\estilo de visualización M}$

• dirigido hacia el futuro si, para cada punto de la curva, el vector tangente está dirigido hacia el futuro.
• dirigido al pasado si, para cada punto de la curva, el vector tangente está dirigido al pasado.

Estas definiciones sólo se aplican a curvas causales (cronológicas o nulas) porque sólo a los vectores tangentes temporales o nulos se les puede asignar una orientación con respecto al tiempo.

• Una curva temporal cerrada es una curva cerrada que en todas partes está dirigida hacia el futuro (o en todas partes está dirigida hacia el pasado).
• Una curva nula cerrada es una curva cerrada que es nula en todas partes dirigida hacia el futuro (o nula en todas partes dirigida hacia el pasado).
• La holonomía de la relación de la tasa de cambio del parámetro afín alrededor de una geodésica nula cerrada es el factor de corrimiento al rojo .

Existen varias relaciones causales entre puntos y en la variedad .${\estilo de visualización x}$${\estilo de visualización y}$${\estilo de visualización M}$

• ${\estilo de visualización x}$ precede cronológicamente (a menudo denotado ) si existe una curva cronológica (similar al tiempo) dirigida al futuro desde hasta .${\estilo de visualización y}$${\displaystyle \,x\ll y}$${\estilo de visualización x}$${\estilo de visualización y}$
• ${\estilo de visualización x}$ precede estrictamente causalmente (a menudo denotado ) si existe una curva causal dirigida al futuro (no espacial) de a .${\estilo de visualización y}$${\displaystyle x<y}$${\estilo de visualización x}$${\estilo de visualización y}$
• ${\estilo de visualización x}$ precede causalmente (a menudo denotado o ) si precede estrictamente causalmente o .${\estilo de visualización y}$${\displaystyle x\precisión y}$${\displaystyle x\leq y}$${\estilo de visualización x}$${\estilo de visualización y}$${\displaystyle x=y}$
• ${\estilo de visualización x}$ horismos ^[3] (a menudo denotado como ) si existe una curva nula dirigida al futuro desde hasta ^[4] (o equivalentemente, y ).${\estilo de visualización y}$${\displaystyle x\to y}$${\displaystyle x\nearrow y}$${\displaystyle x=y}$${\estilo de visualización x}$${\estilo de visualización y}$${\displaystyle x\precisión y}$${\displaystyle x\no \ll y}$

Estas relaciones satisfacen las siguientes propiedades:

• ${\displaystyle x\ll y}$implica (esto se deduce trivialmente de la definición) ^[5]${\displaystyle x\precisión y}$
• ${\displaystyle x\ll y}$, implica ^[5]${\displaystyle y\prec z}$${\displaystyle x\ll z}$
• ${\displaystyle x\precisión y}$, implica ^[5]${\displaystyle y\ll z}$${\displaystyle x\ll z}$
• ${\estilo de visualización \ll}$, , son transitivos . ^[5] no es transitivo. ^[6]${\estilo de visualización <}$${\estilo de visualización \prec}$ ${\displaystyle \to}$
• ${\estilo de visualización \prec}$, son reflexivos ^[4]${\displaystyle \to}$

Para un punto en la variedad definimos ^[5]${\estilo de visualización x}$${\estilo de visualización M}$

• El futuro cronológico de , denotado , como el conjunto de todos los puntos en tales que cronológicamente precede a :${\estilo de visualización x}$${\displaystyle \,I^{+}(x)}$${\estilo de visualización y}$${\estilo de visualización M}$${\estilo de visualización x}$${\estilo de visualización y}$

${\displaystyle \,I^{+}(x)=\{y\en M|x\ll y\}}$

• El pasado cronológico de , denotado , como el conjunto de todos los puntos en tales que cronológicamente precede a :${\estilo de visualización x}$${\displaystyle \,I^{-}(x)}$${\estilo de visualización y}$${\estilo de visualización M}$${\estilo de visualización y}$${\estilo de visualización x}$

${\displaystyle \,I^{-}(x)=\{y\en M|y\ll x\}}$

Definimos de manera similar

• El futuro causal (también llamado futuro absoluto ) de , denotado como el conjunto de todos los puntos en tales que precede causalmente a :${\estilo de visualización x}$${\displaystyle \,J^{+}(x)}$${\estilo de visualización y}$${\estilo de visualización M}$${\estilo de visualización x}$${\estilo de visualización y}$

${\displaystyle \,J^{+}(x)=\{y\in M|x\prec y\}}$

• El pasado causal (también llamado pasado absoluto ) de , denotado como el conjunto de todos los puntos en tales que precede causalmente a :${\displaystyle x}$${\displaystyle \,J^{-}(x)}$${\displaystyle y}$${\displaystyle M}$${\displaystyle y}$${\displaystyle x}$

${\displaystyle \,J^{-}(x)=\{y\in M|y\prec x\}}$

• El futuro cono nulo de como el conjunto de todos los puntos en tales que .${\displaystyle x}$${\displaystyle y}$${\displaystyle M}$${\displaystyle x\to y}$
• El cono nulo pasado de como el conjunto de todos los puntos en tales que .${\displaystyle x}$${\displaystyle y}$${\displaystyle M}$${\displaystyle y\to x}$
• El cono de luz de como los conos nulos futuro y pasado juntos. ^[7]${\displaystyle x}$${\displaystyle x}$
• en otros lugares como puntos que no están en el cono de luz, futuro causal o pasado causal. ^[7]

Los puntos contenidos en , por ejemplo, pueden alcanzarse desde mediante una curva temporal dirigida al futuro. El punto puede alcanzarse, por ejemplo, desde los puntos contenidos en mediante una curva no espacial dirigida al futuro.${\displaystyle \,I^{+}(x)}$${\displaystyle x}$${\displaystyle x}$${\displaystyle \,J^{-}(x)}$

En el espacio-tiempo de Minkowski, el conjunto es el interior del futuro cono de luz en . El conjunto es el cono de luz futuro completo en , incluido el propio cono.${\displaystyle \,I^{+}(x)}$${\displaystyle x}$${\displaystyle \,J^{+}(x)}$${\displaystyle x}$

Estos conjuntos definidos para todos en , se denominan colectivamente la estructura causal de .${\displaystyle \,I^{+}(x),I^{-}(x),J^{+}(x),J^{-}(x)}$${\displaystyle x}$${\displaystyle M}$${\displaystyle M}$

Para un subconjunto de definimos ^[5]${\displaystyle S}$${\displaystyle M}$

${\displaystyle I^{\pm }[S]=\bigcup _{x\in S}I^{\pm }(x)}$

${\displaystyle J^{\pm }[S]=\bigcup _{x\in S}J^{\pm }(x)}$

Para dos subconjuntos de definimos${\displaystyle S,T}$${\displaystyle M}$

• El futuro cronológico de relativo a${\displaystyle S}$${\displaystyle T}$ , , es el futuro cronológico de considerado como una subvariedad de . Nótese que este es un concepto bastante diferente de que da el conjunto de puntos en los que se puede llegar mediante curvas temporales dirigidas al futuro a partir de . En el primer caso, las curvas deben estar en ; en el segundo caso, no. Véase Hawking y Ellis.${\displaystyle I^{+}[S;T]}$${\displaystyle S}$${\displaystyle T}$${\displaystyle I^{+}[S]\cap T}$${\displaystyle T}$${\displaystyle S}$${\displaystyle T}$
• El futuro causal de relativo a${\displaystyle S}$${\displaystyle T}$ , , es el futuro causal de considerado como una subvariedad de . Nótese que este es un concepto bastante diferente de que da el conjunto de puntos en los que se puede llegar mediante curvas causales dirigidas al futuro a partir de . En el primer caso, las curvas deben estar en ; en el segundo caso, no lo están. Véase Hawking y Ellis.${\displaystyle J^{+}[S;T]}$${\displaystyle S}$${\displaystyle T}$${\displaystyle J^{+}[S]\cap T}$${\displaystyle T}$${\displaystyle S}$${\displaystyle T}$
• Un conjunto futuro es un conjunto cerrado bajo el futuro cronológico.
• Un conjunto pasado es un conjunto cerrado bajo el pasado cronológico.
• Un conjunto pasado indecomponible (PI) es un conjunto pasado que no es la unión de dos subconjuntos pasados ​​propios abiertos diferentes.
• Un IP que no coincide con el pasado de ningún punto se denomina conjunto pasado indecomponible terminal (TIP).${\displaystyle M}$
• Un conjunto pasado indescomponible propio (PIP) es un IP que no es un TIP. es un conjunto pasado indescomponible propio (PIP).${\displaystyle I^{-}(x)}$
• El desarrollo futuro de Cauchy de , es el conjunto de todos los puntos para los cuales cada curva causal inextensible dirigida al pasado a través de se interseca al menos una vez. Lo mismo ocurre con el desarrollo pasado de Cauchy. El desarrollo de Cauchy es la unión de los desarrollos futuros y pasados ​​de Cauchy. Los desarrollos de Cauchy son importantes para el estudio del determinismo .${\displaystyle S}$${\displaystyle D^{+}(S)}$${\displaystyle x}$${\displaystyle x}$${\displaystyle S}$
• Un subconjunto es acrónico si no existen tales que , o equivalentemente, si es disjunto de .${\displaystyle S\subset M}$${\displaystyle q,r\in S}$${\displaystyle r\in I^{+}(q)}$${\displaystyle S}$${\displaystyle I^{+}[S]}$

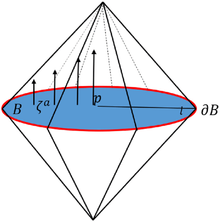
• Una superficie de Cauchy es un conjunto acrónico cerrado cuyo desarrollo de Cauchy es .${\displaystyle M}$
• Una métrica es globalmente hiperbólica si puede ser foliada por superficies de Cauchy.
• El conjunto que viola la cronología es el conjunto de puntos por donde pasan curvas temporales cerradas.
• El conjunto que viola la causalidad es el conjunto de puntos por donde pasan curvas causales cerradas.
• El límite del conjunto que viola la causalidad es un horizonte de Cauchy . Si el horizonte de Cauchy se genera mediante geodésicas nulas cerradas, entonces hay un factor de corrimiento al rojo asociado con cada una de ellas.
• Para una curva causal , el diamante causal es (aquí usamos la definición más flexible de 'curva', en la que es solo un conjunto de puntos), siendo el punto en el pasado causal de . En palabras: el diamante causal de la línea de mundo de una partícula es el conjunto de todos los eventos que se encuentran tanto en el pasado de algún punto en como en el futuro de algún punto en . En la versión discreta, el diamante causal es el conjunto de todos los caminos causales que se conectan desde .${\displaystyle \gamma }$${\displaystyle J^{+}(\gamma (t_{1}))\cap J^{-}(\gamma (t_{2}))}$${\displaystyle \gamma (t_{1})}$${\displaystyle \gamma (t_{2})}$${\displaystyle \gamma }$${\displaystyle \gamma }$${\displaystyle \gamma }$${\displaystyle \gamma (t_{2})}$${\displaystyle \gamma (t_{1})}$

Véase Penrose (1972), pág. 13.

• Un punto está en si y sólo si está en .${\displaystyle x}$${\displaystyle \,I^{-}(y)}$${\displaystyle y}$${\displaystyle \,I^{+}(x)}$
• ${\displaystyle x\prec y\implies I^{-}(x)\subset I^{-}(y)}$
• ${\displaystyle x\prec y\implies I^{+}(y)\subset I^{+}(x)}$
• ${\displaystyle I^{+}[S]=I^{+}[I^{+}[S]]\subset J^{+}[S]=J^{+}[J^{+}[S]]}$
• ${\displaystyle I^{-}[S]=I^{-}[I^{-}[S]]\subset J^{-}[S]=J^{-}[J^{-}[S]]}$
• El horismos se genera por congruencias geodésicas nulas.

Propiedades topológicas :

• ${\displaystyle I^{\pm }(x)}$está abierto para todos los puntos en .${\displaystyle x}$${\displaystyle M}$
• ${\displaystyle I^{\pm }[S]}$está abierto para todos los subconjuntos .${\displaystyle S\subset M}$
• ${\displaystyle I^{\pm }[S]=I^{\pm }[{\overline {S}}]}$para todos los subconjuntos . Aquí está el cierre de un subconjunto .${\displaystyle S\subset M}$${\displaystyle {\overline {S}}}$${\displaystyle S}$
• ${\displaystyle I^{\pm }[S]\subset {\overline {J^{\pm }[S]}}}$

Dos métricas y están relacionadas conformemente ^[8] si para alguna función real llamada factor conforme . (Ver mapa conforme ).${\displaystyle \,g}$${\displaystyle {\hat {g}}}$${\displaystyle {\hat {g}}=\Omega ^{2}g}$${\displaystyle \Omega }$

Si observamos las definiciones de qué vectores tangentes son temporales, nulos y espaciales, vemos que permanecen invariables si usamos o . Como ejemplo, supongamos que es un vector tangente temporal con respecto a la métrica. Esto significa que . Entonces tenemos que por lo tanto es un vector tangente temporal con respecto a también.${\displaystyle \,g}$${\displaystyle {\hat {g}}}$${\displaystyle X}$${\displaystyle \,g}$${\displaystyle \,g(X,X)<0}$${\displaystyle {\hat {g}}(X,X)=\Omega ^{2}g(X,X)<0}$${\displaystyle X}$${\displaystyle {\hat {g}}}$

De esto se desprende que la estructura causal de una variedad lorentziana no se ve afectada por una transformación conforme .

Una geodésica nula sigue siendo una geodésica nula bajo un reescalamiento conforme.

Una métrica infinita admite geodésicas de longitud/tiempo propio infinitos. Sin embargo, a veces podemos hacer un reescalamiento conforme de la métrica con un factor conforme que cae lo suficientemente rápido a 0 a medida que nos acercamos al infinito para obtener el límite conforme de la variedad. La estructura topológica del límite conforme depende de la estructura causal.

• Las geodésicas temporales dirigidas hacia el futuro terminan en , el futuro infinito temporal .${\displaystyle i^{+}}$
• Las geodésicas temporales dirigidas al pasado terminan en , el infinito temporal pasado .${\displaystyle i^{-}}$
• Las geodésicas nulas dirigidas al futuro terminan en ℐ ⁺ , el futuro infinito nulo .
• Las geodésicas nulas dirigidas al pasado terminan en ℐ ⁻ , el infinito nulo pasado .
• Las geodésicas espaciales terminan en el infinito espacial .

En varios espacios:

• Espacio de Minkowski : son puntos, ℐ ^± son láminas nulas y el infinito espacial tiene codimensión 2.${\displaystyle i^{\pm }}$
• Espacio anti-de Sitter : no hay infinito temporal o nulo, y el infinito espacial tiene codimensión 1.
• Espacio de Sitter : el tiempo futuro y pasado, como el infinito, tiene codimensión 1.

Si una geodésica termina después de un parámetro afín finito, y no es posible extender la variedad para extender la geodésica, entonces tenemos una singularidad .

• Para los agujeros negros , el límite temporal futuro termina en una singularidad en algunos lugares.
• Para el Big Bang , el límite temporal pasado también es una singularidad.

El horizonte de sucesos absoluto es el cono nulo pasado del infinito temporal futuro. Se genera mediante geodésicas nulas que obedecen a la ecuación óptica de Raychaudhuri .

• Triangulación dinámica causal (CDT)
• Condiciones de causalidad
• Conjuntos causales
• Superficie de Cauchy
• Curva temporal cerrada
• Hipótesis de la censura cósmica
• Variedad hiperbólica global
• Espacio-tiempo de Malament-Hogarth
• Infinito nulo
• Diagrama de Penrose
• Teoremas de singularidad de Penrose-Hawking
• Espacio-tiempo

• Hawking, SW ; Ellis, GFR (1973), La estructura a gran escala del espacio-tiempo , Cambridge: Cambridge University Press, ISBN 0-521-20016-4
• Hawking, SW ; Israel, W. (1979), Relatividad general, una encuesta del centenario de Einstein , Cambridge University Press, ISBN 0-521-22285-0
• Penrose, R. (1972), Técnicas de topología diferencial en relatividad , SIAM, ISBN 0898710057
• Sard, RD (1970). Mecánica relativista: relatividad especial y dinámica clásica de partículas . Nueva York: WA Benjamin. ISBN 978-0805384918.

• Redes causales de la máquina de Turing por Enrique Zeleny, Proyecto de Demostraciones Wolfram
• Weisstein, Eric W. "Red causal". MathWorld .