Acorde (aeronáutica)

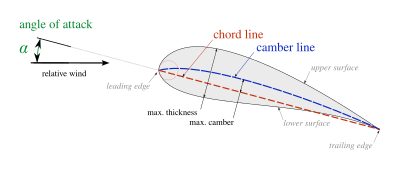
En aeronáutica , la cuerda es una línea recta imaginaria que une el borde de ataque y el borde de salida de un perfil aerodinámico . La longitud de la cuerda es la distancia entre el borde de salida y el punto donde la cuerda interseca el borde de ataque. ^{[1] [2]} El punto en el borde de ataque utilizado para definir la cuerda puede ser el punto de superficie de radio mínimo. ^[2] Para un perfil aerodinámico de turbina, la cuerda puede definirse por la línea entre los puntos donde la parte delantera y trasera de una sección de pala bidimensional tocarían una superficie plana cuando se coloca con el lado convexo hacia arriba. ^[3]

El ala , el estabilizador horizontal , el estabilizador vertical y las palas de la hélice /rotor de una aeronave se basan en secciones aerodinámicas, y el término cuerda o longitud de cuerda también se utiliza para describir su ancho. La cuerda de un ala, estabilizador y hélice se determina midiendo la distancia entre los bordes de ataque y de salida en la dirección del flujo de aire. (Si un ala tiene una forma en planta rectangular , en lugar de cónica o en flecha, entonces la cuerda es simplemente el ancho del ala medido en la dirección del flujo de aire). El término cuerda también se aplica al ancho de los flaps , alerones y timón de dirección de una aeronave.

El término también se aplica a los perfiles aerodinámicos de compresores y turbinas en motores de turbina de gas , como turborreactores , turbohélices o turbofán para la propulsión de aeronaves.

Muchas alas no son rectangulares, por lo que tienen diferentes cuerdas en diferentes posiciones. Por lo general, la longitud de la cuerda es mayor donde el ala se une al fuselaje de la aeronave (llamada cuerda de raíz ) y disminuye a lo largo del ala hacia la punta del ala ( cuerda de punta ). La mayoría de los aviones a reacción utilizan un diseño de ala en flecha cónica . Para proporcionar una figura característica que se pueda comparar entre varias formas de alas, se utiliza la cuerda aerodinámica media (abreviada MAC ), aunque es compleja de calcular. La cuerda aerodinámica media se utiliza para calcular los momentos de cabeceo. ^[4]

La cuerda media estándar (SMC) se define como el área del ala dividida por la envergadura: ^[5]

${\displaystyle {\mbox{SMC}}={\frac {S}{b}},}$

donde S es el área del ala y b es la envergadura del ala. Por lo tanto, el SMC es la cuerda de un ala rectangular con la misma área y envergadura que las del ala dada. Esta es una figura puramente geométrica y rara vez se utiliza en aerodinámica .

La cuerda aerodinámica media (CAM) se define como: ^[6]

${\displaystyle {\mbox{MAC}}={\frac {2}{S}}}$${\displaystyle \int _{0}^{\frac {b}{2}}c(y)^{2}dy,}$

donde y es la coordenada a lo largo de la envergadura del ala y c es la cuerda en la coordenada y . Los demás términos son los mismos que para SMC.

El MAC es una representación bidimensional de toda el ala. La distribución de la presión sobre toda el ala se puede reducir a una única fuerza de sustentación y un momento alrededor del centro aerodinámico del MAC. Por lo tanto, no solo la longitud, sino también la posición del MAC son a menudo importantes. En particular, la posición del centro de gravedad (CG) de una aeronave se mide normalmente en relación con el MAC, como el porcentaje de la distancia desde el borde de ataque del MAC hasta el CG con respecto al propio MAC.

Tenga en cuenta que la figura de la derecha implica que el MAC se produce en un punto en el que cambia el barrido del borde de entrada o de salida. Eso es solo una coincidencia. En general, este no es el caso. Cualquier forma que no sea un simple trapezoide requiere la evaluación de la integral anterior.

La relación entre la longitud (o envergadura ) de un ala de planta rectangular y su cuerda se conoce como relación de aspecto , un indicador importante de la resistencia inducida por sustentación que creará el ala. ^[7] (Para alas con formas de planta que no son rectangulares, la relación de aspecto se calcula como el cuadrado de la envergadura dividido por el área de la forma de planta del ala). Las alas con relaciones de aspecto más altas tendrán menos resistencia inducida que las alas con relaciones de aspecto más bajas. La resistencia inducida es más significativa a bajas velocidades aerodinámicas. Es por eso que los planeadores tienen alas largas y delgadas.

Conociendo el área (S _w ), la relación de conicidad ( ) y la envergadura (b) del ala, la cuerda en cualquier posición de la envergadura se puede calcular mediante la fórmula: ^[8]${\estilo de visualización \lambda}$

${\displaystyle c(y)={\frac {2\,S_{w}}{(1+\lambda )b}}\left[1-{\frac {1-\lambda }{b}}|2y|\right].}$

dónde

${\displaystyle \lambda ={\frac {C_{\rm {Punta}}}{C_{\rm {Raíz}}}}}$

• Aerodinámica para estudiantes
  • máquina del tiempo:[1]
• Encontrar la cuerda aerodinámica media (MAC)
• Calculadora de cuerda aerodinámica media (MAC) basada en imágenes