Copa Faraday

Copa Faraday

Diagrama esquemático de una copa de Faraday
Usos	Detector de partículas cargadas
Artículos relacionados	Multiplicador de electrones Detector de placas de microcanal Detector Daly

Una copa de Faraday es una copa de metal (conductora) diseñada para atrapar partículas cargadas . La corriente resultante se puede medir y utilizar para determinar la cantidad de iones o electrones que golpean la copa. ^[1] La copa de Faraday debe su nombre a Michael Faraday, quien teorizó por primera vez sobre los iones alrededor de 1830.

Entre los dispositivos que utilizan copas de Faraday se incluyen las sondas espaciales ( Voyager 1 y 2 , Parker Solar Probe , etc.) y los espectrómetros de masas . Las copas de Faraday también se pueden utilizar para medir partículas de aerosol cargadas.

Cuando un haz o paquete de iones o electrones (por ejemplo, de un haz de electrones ) golpea el cuerpo metálico del vaso, el aparato obtiene una pequeña carga neta. El vaso puede entonces descargarse para medir una pequeña corriente proporcional a la carga transportada por los iones o electrones que chocan. Al medir la corriente eléctrica (la cantidad de electrones que fluyen a través del circuito por segundo) en el vaso, se puede determinar la cantidad de cargas. Para un haz continuo de iones (que se supone que tienen una sola carga) o electrones, la cantidad total N que golpea el vaso por unidad de tiempo (en segundos) es

${\displaystyle {\frac {N}{t}}={\frac {I}{e}}}$

donde I es la corriente medida (en amperios ) y e es la carga elemental (1,60 × 10 ⁻¹⁹ C ). Por lo tanto, una corriente medida de un nanoamperio (10 ⁻⁹ A) corresponde a aproximadamente 6 mil millones de partículas con carga simple que golpean la copa Faraday cada segundo.

Las copas de Faraday no son tan sensibles como los detectores multiplicadores de electrones , pero son muy valorados por su precisión debido a la relación directa entre la corriente medida y el número de iones.

Esta sección puede ser demasiado técnica para que la mayoría de los lectores la comprendan . Ayúdenos a mejorarla para que sea comprensible para los no expertos , sin eliminar los detalles técnicos. ( Septiembre de 2019 ) ( Aprenda cómo y cuándo eliminar este mensaje )

La copa de Faraday utiliza un principio físico según el cual las cargas eléctricas entregadas a la superficie interna de un conductor hueco se redistribuyen alrededor de su superficie externa debido a la autorrepulsión mutua de cargas del mismo signo, un fenómeno descubierto por Faraday . ^[2]

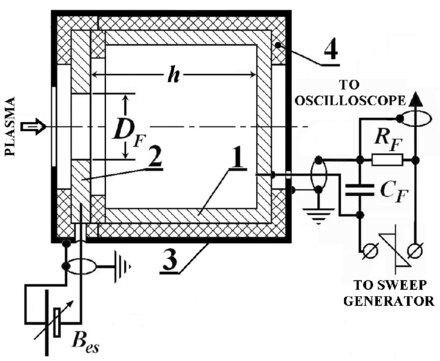
La copa Faraday convencional se aplica para mediciones de flujos de iones (o electrones) desde los límites del plasma y comprende una copa receptora cilíndrica metálica - 1 (Fig. 1) cerrada con, y aislada de, una tapa supresora de electrones metálica tipo arandela - 2 provista de la cavidad de entrada axial redonda de una abertura con un área de superficie . Tanto la copa receptora como la tapa supresora de electrones están envueltas en, y aisladas de, un blindaje cilíndrico conectado a tierra - 3 que tiene un orificio redondo axial que coincide con el orificio en la tapa supresora de electrones - 2. La tapa supresora de electrones está conectada por un cable RF de 50 Ω con la fuente de voltaje CC variable . La copa receptora está conectada por un cable RF de 50 Ω a través de la resistencia de carga con un generador de barrido que produce pulsos tipo sierra . La capacidad eléctrica está formada por la capacidad de la copa receptora - 1 al blindaje conectado a tierra - 3 y la capacidad del cable RF. La señal de permite a un observador obtener una característica IV de la copa de Faraday mediante un osciloscopio. Condiciones de funcionamiento adecuadas: (debido a una posible caída de potencial) y , donde es el camino libre de iones. La señal de es la característica IV de la copa de Faraday que se puede observar y memorizar mediante un osciloscopio.${\displaystyle S_{F}=\pi D_{F}^{2}/4}$${\displaystyle B_{es}}$${\displaystyle U_{es}}$$Estilo de visualización: R_{F}$$Estilo de visualización U_{g}(t)}$$Estilo de visualización C_{F}$$Estilo de visualización: R_{F}$${\displaystyle h\geq D_{F}}$${\displaystyle h\ll \lambda _{i}}$${\displaystyle \lambda _{i}}$$Estilo de visualización: R_{F}$

${\displaystyle i_{\Sigma}(U_{g})=i_{i}(U_{g})-C_{F}{\frac {dU_{g}}{dt}}}$

( 1 )

En la Fig. 1: 1 – recipiente receptor, de metal (acero inoxidable). 2 – tapa supresora de electrones, de metal (acero inoxidable). 3 – blindaje puesto a tierra, de metal (acero inoxidable). 4 – aislante (teflón, cerámica). – capacidad del recipiente Faraday. – resistencia de carga.$Estilo de visualización C_{F}$$Estilo de visualización: R_{F}$

De esta manera, medimos la suma de las corrientes eléctricas a través de la resistencia de carga : (corriente de la copa de Faraday) más la corriente inducida a través del condensador por el voltaje tipo sierra del generador de barrido: El componente de corriente se puede medir en ausencia del flujo de iones y se puede restar aún más de la corriente total medida con plasma para obtener la característica IV real de la copa de Faraday para el procesamiento. Todos los elementos de la copa de Faraday y su ensamblaje que interactúan con el plasma se fabrican generalmente de materiales resistentes a la temperatura (a menudo, estos son acero inoxidable y teflón o cerámica para aislantes). Para el procesamiento de la característica IV de la copa de Faraday , vamos a suponer que la copa de Faraday está instalada lo suficientemente lejos de una fuente de plasma investigada donde el flujo de iones podría considerarse como el flujo de partículas con velocidades paralelas dirigidas exactamente a lo largo del eje de la copa de Faraday. En este caso, la corriente de partículas elementales correspondiente al diferencial de densidad de iones en el rango de velocidades entre y de iones que fluyen a través de la apertura operativa del supresor de electrones se puede escribir en la forma${\displaystyle i_{\Sigma}}$$Estilo de visualización: R_{F}$${\displaystyle i_{i}}$${\displaystyle i_{c}(U_{g})=-C_{F}(dU_{g}/dt)}$$Estilo de visualización C_{F}$${\displaystyle U_{g}}$${\displaystyle i_{c}(U_{g})}$${\displaystyle i_{\Sigma}(U_{g})}$ ${\displaystyle i_{i}(U_{g})}$$Estilo de visualización di_{i}}$${\displaystyle dn(v)}$${\estilo de visualización v}$${\estilo de visualización v+dv}$$Estilo de visualización S_ {F}}$

${\displaystyle di_{i}=eZ_{i}S_{F}vdn(v)}$

( 2 )

dónde

${\displaystyle dn(v)=nf(v)dv}$

( 3 )

${\estilo de visualización e}$es la carga elemental, es el estado de carga iónica y es la función de distribución de velocidad iónica unidimensional. Por lo tanto, la corriente iónica en el voltaje de desaceleración iónica de la copa de Faraday se puede calcular integrando la ecuación ( 2 ) después de sustituir la ecuación ( 3 ),$Estilo de visualización Z_{i}}$${\displaystyle f(v)}$${\displaystyle U_{g}}$

${\displaystyle i_{i}(U_{g})=eZ_{i}n_{i}S_{F}\int \limits _{\sqrt {2eZ_{i}U_{g}/M_{i}}}^{\infty }f(v)vdv}$

( 4 )

donde el límite de integración inferior se define a partir de la ecuación donde es la velocidad del ion detenido por el potencial de desaceleración , y es la masa del ion. Por lo tanto, la ecuación ( 4 ) representa la característica IV de la copa de Faraday. Diferenciando la ecuación ( 4 ) con respecto a , se puede obtener la relación${\displaystyle M_{i}v_{i,s}^{2}/2=eZ_{i}U_{g}}$${\displaystyle v_{i,s}}$${\displaystyle U_{g}}$${\displaystyle M_{i}}$${\displaystyle U_{g}}$

${\displaystyle {\frac {di_{i}(U_{g})}{dU_{g}}}=-en_{i}S_{F}{\frac {eZ_{i}}{M_{i}}}f\left({\sqrt {\frac {2eZ_{i}U_{g}}{M_{i}}}}\right)}$

( 5 )

donde el valor es una constante invariable para cada medida. Por lo tanto, la velocidad media de los iones que llegan a la copa de Faraday y su energía media se pueden calcular (suponiendo que operamos con un único tipo de ion) mediante las expresiones${\displaystyle -n_{i}S_{F}(eZ_{i}/M_{i})=C_{i}}$${\displaystyle \langle v_{i}\rangle }$${\displaystyle \langle {\mathcal {E}}_{i}\rangle }$

${\displaystyle \langle v_{i}\rangle =1.389\times 10^{6}{\sqrt {\frac {Z_{i}}{M_{A}}}}\int \limits _{0}^{\infty }i_{i}^{\prime }(U_{g})dU_{g}\left(\int \limits _{0}^{\infty }{\frac {i_{i}^{\prime }}{\sqrt {U_{g}}}}dU_{g}\right)^{-1}}$ [cm/s]

( 6 )

${\displaystyle \langle {\mathcal {E}}_{i}\rangle =\int \limits _{0}^{\infty }i_{i}^{\prime }(U_{g}){\sqrt {U_{g}}}dU_{g}\left(\int \limits _{0}^{\infty }{\frac {i_{i}^{\prime }}{\sqrt {U_{g}}}}dU_{g}\right)^{-1}}$ [eV]

( 7 )

donde es la masa del ion en unidades atómicas. La concentración de iones en el flujo de iones en las proximidades de la copa de Faraday se puede calcular mediante la fórmula${\displaystyle M_{A}}$${\displaystyle n_{i}}$

${\displaystyle n_{i}={\frac {i_{i}(0)}{eZ_{i}\langle v_{i}\rangle S_{F}}}}$

( 8 )

lo cual se sigue de la ecuación ( 4 ) en ,${\displaystyle U_{g}=0}$

${\displaystyle \int \limits _{0}^{\infty }f(v)vdv=\langle v\rangle }$

( 9 )

y de la condición convencional para la normalización de la función de distribución

${\displaystyle \int \limits _{0}^{\infty }f(v)dv=1}$

( 10 )

La figura 2 ilustra la característica IV y su primera derivada de la copa Faraday instalada en la salida de la fuente de plasma acoplada inductivamente alimentada con RF 13,56 MHz y que opera a 6 mTorr de H2. El valor del voltaje del supresor de electrones (que acelera los iones) se estableció experimentalmente en , cerca del punto de supresión de la emisión de electrones secundarios desde la superficie interna de la copa Faraday. ^[3]${\displaystyle i_{i}(V)}$${\displaystyle i_{i}^{\prime }(V)}$${\displaystyle S_{F}=0.5cm^{2}}$${\displaystyle U_{es}=-170V}$

El recuento de cargas recogidas por unidad de tiempo se ve afectado por dos fuentes de error: 1) la emisión de electrones secundarios de baja energía desde la superficie golpeada por la carga incidente y 2) la retrodispersión (dispersión de ~180 grados) de la partícula incidente, que hace que abandone la superficie de recogida, al menos temporalmente. Especialmente con los electrones, es fundamentalmente imposible distinguir entre un electrón incidente nuevo y uno que ha sido retrodispersado o incluso un electrón secundario rápido.

• Nanoculombimetro
• Multiplicador de electrones
• Detector de placa de microcanales
• Detector diario
• Electrómetro de copa Faraday
• Jaula de Faraday
• Constante de Faraday
• BARRIDO

• Detección de iones en espectrómetros de masas con la copa de Faraday Por Kenneth L. Busch