Sistema de coordenadas cilíndricas

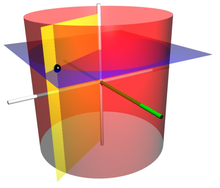
Un sistema de coordenadas cilíndricas es un sistema de coordenadas tridimensional que especifica las posiciones de los puntos mediante la distancia desde un eje de referencia elegido (eje L en la imagen opuesta) , la dirección desde el eje en relación con una dirección de referencia elegida (eje A) y la distancia desde un plano de referencia elegido perpendicular al eje (plano que contiene la sección violeta) . La última distancia se da como un número positivo o negativo según qué lado del plano de referencia esté orientado hacia el punto.

El origen del sistema es el punto en el que las tres coordenadas pueden darse como cero. Esta es la intersección entre el plano de referencia y el eje. El eje se denomina de diversas formas: eje cilíndrico o eje longitudinal , para diferenciarlo del eje polar , que es el rayo que se encuentra en el plano de referencia, comenzando en el origen y apuntando en la dirección de referencia. Otras direcciones perpendiculares al eje longitudinal se denominan líneas radiales .

La distancia desde el eje puede denominarse distancia radial o radio , mientras que la coordenada angular se denomina a veces posición angular o acimut . El radio y el acimut se denominan en conjunto coordenadas polares , ya que corresponden a un sistema de coordenadas polares bidimensionales en el plano que pasa por el punto, paralelo al plano de referencia. La tercera coordenada puede denominarse altura o altitud (si el plano de referencia se considera horizontal), posición longitudinal ^[1] o posición axial ^[2] .

Las coordenadas cilíndricas son útiles en relación con objetos y fenómenos que tienen cierta simetría rotacional alrededor del eje longitudinal, como el flujo de agua en una tubería recta con sección transversal redonda, la distribución de calor en un cilindro de metal , los campos electromagnéticos producidos por una corriente eléctrica en un cable largo y recto, los discos de acreción en astronomía, etc.

A veces se denominan "coordenadas polares cilíndricas" ^[3] y "coordenadas cilíndricas polares", ^[4] y a veces se utilizan para especificar la posición de las estrellas en una galaxia ("coordenadas polares cilíndricas galactocéntricas"). ^[5]

Las tres coordenadas ( ρ , φ , z ) de un punto P se definen como:

• La distancia radial ρ es la distancia euclidiana desde el eje z hasta el punto P.
• El acimut φ es el ángulo entre la dirección de referencia en el plano elegido y la línea desde el origen hasta la proyección de P en el plano.
• La coordenada axial o altura z es la distancia con signo desde el plano elegido hasta el punto P.

Al igual que en las coordenadas polares, el mismo punto con coordenadas cilíndricas ( ρ , φ , z ) tiene infinitas coordenadas equivalentes, a saber ( ρ , φ ± n ×360°, z ) y (− ρ , φ ± (2 n + 1)×180°, z ), donde n es cualquier número entero. Además, si el radio ρ es cero, el acimut es arbitrario.

En situaciones donde alguien desea un conjunto único de coordenadas para cada punto, se puede restringir que el radio no sea negativo ( ρ ≥ 0 ) y que el acimut φ se encuentre en un intervalo específico que abarque 360°, como [−180°,+180°] o [0,360°] .

La notación para las coordenadas cilíndricas no es uniforme. La norma ISO 31-11 recomienda ( ρ , φ , z ) , donde ρ es la coordenada radial, φ el acimut y z la altura. Sin embargo, el radio también suele denotarse como r o s , el acimut como θ o t y la tercera coordenada como h o (si el eje cilíndrico se considera horizontal) x , o cualquier letra específica del contexto.

En situaciones concretas y en muchas ilustraciones matemáticas, una coordenada angular positiva se mide en sentido antihorario, vista desde cualquier punto con altura positiva.

El sistema de coordenadas cilíndricas es uno de los muchos sistemas de coordenadas tridimensionales. Las siguientes fórmulas se pueden utilizar para realizar conversiones entre ellos.

Para la conversión entre coordenadas cilíndricas y cartesianas, es conveniente suponer que el plano de referencia de las primeras es el plano cartesiano xy (con ecuación z = 0 ), y el eje cilíndrico es el eje cartesiano z . Entonces la coordenada z es la misma en ambos sistemas, y la correspondencia entre las coordenadas cilíndricas ( ρ , φ , z ) y cartesianas ( x , y , z ) son las mismas que para las coordenadas polares, es decir, en una dirección y en la otra. La función arcoseno es la inversa de la función seno , y se supone que devuelve un ángulo en el rango [− ⁠$${\displaystyle {\begin{aligned}x&=\rho \cos \varphi \\y&=\rho \sin \varphi \\z&=z\end{aligned}}}$$$${\displaystyle {\begin{aligned}\rho &={\sqrt {x^{2}+y^{2}}}\\\varphi &={\begin{cases}{\text{indeterminado}}&{\text{si }}x=0{\text{ y }}y=0\\\arcsin \left({\frac {y}{\rho }}\right)&{\text{si }}x\geq 0\\-\arcsin \left({\frac {y}{\rho }}\right)+\pi &{\mbox{si }}x<0{\text{ y }}y\geq 0\\-\arcsin \left({\frac {y}{\rho }}\right)+\pi &{\mbox{si }}x<0{\text{ y }}y<0\end{casos}}\end{alineado}}}$$π/2⁠ , + ⁠π/2⁠ ] = [−90°, +90°] . Estas fórmulas dan como resultado un acimut φ en el rango [−90°, +270°] .

Utilizando la función arcotangente que devuelve también un ángulo en el rango [− ⁠π/2⁠ , + ⁠π/2⁠ ] = [−90°, +90°] , también se puede calcularsin calcularprimero Para otras fórmulas, consulte el artículo Sistema de coordenadas polares .${\estilo de visualización \varphi}$${\estilo de visualización \rho}$$${\displaystyle {\begin{aligned}\varphi &={\begin{cases}{\text{indeterminado}}&{\text{si }}x=0{\text{ y }}y=0\\{\frac {\pi }{2}}{\frac {y}{|y|}}&{\text{si }}x=0{\text{ y }}y\neq 0\\\arctan \left({\frac {y}{x}}\right)&{\mbox{si }}x>0\\\arctan \left({\frac {y}{x}}\right)+\pi &{\mbox{si }}x<0{\text{ y }}y\geq 0\\\arctan \left({\frac {y}{x}}\right)-\pi &{\mbox{si }}x<0{\text{ y }}y<0\end{casos}}\end{alineado}}}$$

Muchos lenguajes de programación modernos proporcionan una función que calcula el acimut correcto φ , en el rango (−π, π) , dados x e y , sin necesidad de realizar un análisis de caso como el anterior. Por ejemplo, esta función es invocada por atan2 ( y , x ) en el lenguaje de programación C , y (atan y x ) en Common Lisp .

Las coordenadas esféricas (radio r , elevación o inclinación θ , acimut φ ), se pueden convertir a o desde coordenadas cilíndricas, dependiendo de si θ representa elevación o inclinación, de la siguiente manera:

Conversión entre coordenadas esféricas y cilíndricas

Conversión a:	Coordinar	θ es la elevación	θ es inclinación
Cilíndrico	ρ =	r cos θ	r pecado θ
	φ =	φ
	z =	r pecado θ	r cos θ
Esférico	r =	${\textstyle {\sqrt {\rho ^{2}+z^{2}}}}$
	θ =	${\textstyle \arctan \izquierda({\frac {z}{\rho }}\derecha)}$	${\textstyle \arctan \left({\frac {\rho }{z}}\right)}$
	φ =	φ

En muchos problemas que involucran coordenadas polares cilíndricas, es útil conocer los elementos de línea y volumen; estos se utilizan en la integración para resolver problemas que involucran trayectorias y volúmenes.

El elemento de línea es$${\displaystyle \mathrm {d} {\boldsymbol {r}}=\mathrm {d} \rho \,{\boldsymbol {\hat {\rho }}}+\rho \,\mathrm {d} \varphi \ ,{\boldsymbol {\hat {\varphi }}}+\mathrm {d} z\,{\boldsymbol {\hat {z}}}.}$$

El elemento de volumen es$${\displaystyle \mathrm {d} V=\rho \,\mathrm {d} \rho \,\mathrm {d} \varphi \,\mathrm {d} z.}$$

El elemento de superficie en una superficie de radio constante ρ (un cilindro vertical) es$${\displaystyle \mathrm {d} S_{\rho }=\rho \,\mathrm {d} \varphi \,\mathrm {d} z.}$$

El elemento de superficie en una superficie de acimut constante φ (un semiplano vertical) es$${\displaystyle \mathrm {d} S_{\varphi }=\mathrm {d} \rho \,\mathrm {d} z.}$$

El elemento de superficie en una superficie de altura constante z (un plano horizontal) es$${\displaystyle \mathrm {d} S_{z}=\rho \,\mathrm {d} \rho \,\mathrm {d} \varphi .}$$

El operador del en este sistema conduce a las siguientes expresiones para gradiente , divergencia , rizo y laplaciano :$${\displaystyle {\begin{aligned}\nabla f&={\frac {\partial f}{\partial \rho }}{\boldsymbol {\hat {\rho }}}+{\frac {1}{\rho }}{\frac {\partial f}{\partial \varphi }}{\boldsymbol {\hat {\varphi }}}+{\frac {\partial f}{\partial z}}{\boldsymbol {\hat {z}}}\\[8px]\nabla \cdot {\boldsymbol {A}}&={\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}\left(\rho A_{\rho }\right)+{\frac {1}{\rho }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+{\frac {\partial A_{z}}{\partial z}}\\[8px]\nabla \times {\boldsymbol {A}}&=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right){\boldsymbol {\hat {\rho }}}+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\boldsymbol {\hat {\varphi }}}+{\frac {1}{\rho }}\left({\frac {\partial }{\partial \rho }}\left(\rho A_{\varphi }\right)-{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\boldsymbol {\hat {z}}}\\[8px]\nabla ^{2}f&={\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}\left(\rho {\frac {\partial f}{\partial \rho }}\right)+{\frac {1}{\rho ^{2}}}{\frac {\partial ^{2}f}{\partial \varphi ^{2}}}+{\frac {\partial ^{2}f}{\partial z^{2}}}\end{aligned}}}$$

Las soluciones de la ecuación de Laplace en un sistema con simetría cilíndrica se denominan armónicos cilíndricos .

En un sistema de coordenadas cilíndricas, la posición de una partícula se puede escribir como ^[6] La velocidad de la partícula es la derivada temporal de su posición, donde el término proviene de la fórmula de Poisson . Su aceleración es ^[6]$${\displaystyle {\boldsymbol {r}}=\rho \,{\boldsymbol {\hat {\rho }}}+z\,{\boldsymbol {\hat {z}}}.}$$$${\displaystyle {\boldsymbol {v}}={\frac {\mathrm {d} {\boldsymbol {r}}}{\mathrm {d} t}}={\dot {\rho }}\,{\boldsymbol {\hat {\rho }}}+\rho \,{\dot {\varphi }}\,{\hat {\boldsymbol {\varphi }}}+{\dot {z}}\,{\hat {\boldsymbol {z}}},}$$${\displaystyle \rho {\dot {\varphi }}{\hat {\varphi }}}$${\displaystyle {\frac {\mathrm {d} {\hat {\rho }}}{\mathrm {d} t}}={\dot {\varphi }}{\hat {z}}\times {\hat {\rho }}}$$${\displaystyle {\boldsymbol {a}}={\frac {\mathrm {d} {\boldsymbol {v}}}{\mathrm {d} t}}=\left({\ddot {\rho }}-\rho \,{\dot {\varphi }}^{2}\right){\boldsymbol {\hat {\rho }}}+\left(2{\dot {\rho }}\,{\dot {\varphi }}+\rho \,{\ddot {\varphi }}\right){\hat {\boldsymbol {\varphi }}}+{\ddot {z}}\,{\hat {\boldsymbol {z}}}}$$

• Lista de transformaciones de coordenadas canónicas
• Campos vectoriales en coordenadas cilíndricas y esféricas
• Del en coordenadas cilíndricas y esféricas

• Morse, Philip M. ; Feshbach, Herman (1953). Métodos de física teórica, parte I . Nueva York : McGraw-Hill . págs. 656–657. ISBN 0-07-043316-X. Código LCCN  52011515.
• Margenau, Henry ; Murphy, George M. (1956). Matemáticas de la física y la química . Nueva York: D. van Nostrand. p. 178. ISBN 9780882754239. LCCN  55010911. OCLC  3017486.
• Korn, Granino A.; Korn, Theresa M. (1961). Manual matemático para científicos e ingenieros . Nueva York: McGraw-Hill. págs. 174-175. LCCN  59014456. ASIN B0000CKZX7.
• Sauer, Robert; Szabó, István (1967). Mathematische Hilfsmittel des Ingenieurs . Ciudad de Nueva York: Springer-Verlag . pag. 95.LCCN 67025285  .
• Zwillinger, Daniel (1992). Manual de integración . Boston : Jones and Bartlett Publishers . pág. 113. ISBN. 0-86720-293-9.OCLC 25710023  .
• Moon, P.; Spencer, DE (1988). "Coordenadas de cilindros circulares (r, ψ, z)". Manual de teoría de campos, incluidos sistemas de coordenadas, ecuaciones diferenciales y sus soluciones (2.ª edición corregida). Nueva York: Springer-Verlag. págs. 12-17, tabla 1.02. ISBN 978-0-387-18430-2.

• "Coordenadas de cilindros", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Descripción de las coordenadas cilíndricas en MathWorld
• Animaciones de coordenadas cilíndricas que ilustran coordenadas cilíndricas de Frank Wattenberg